光子雷达探测性能与测距精度的理论研究

罗韩君，周仁龙，张禹涛

（湖南科技大学物理与电子科学学院，湘潭411201）

光子雷达探测性能与测距精度的理论研究

罗韩君，周仁龙，张禹涛

（湖南科技大学物理与电子科学学院，湘潭411201）

为了研究基于盖革模式雪崩光电二极管探测器的光子雷达的探测性能与测距精度，采用数学建模的方法，从系统原理与探测时序出发，分析了长死时间、回波脉宽大于时间数字转换器分辨时间情况下目标探测概率的分布；由统计原理与质心法，建立了测距精度的理论模型。利用系统设计参量，分析了回波强度、回波脉宽、噪声和回波位置等参量对探测性能和测距精度的影响。结果表明，回波越强，噪声越低，回波位置越靠前，目标探测概率越高，虚警率越低，探测性能越好；回波强度和脉宽是影响测距精度的主要因素，回波强度越强，脉宽越窄，测距精度越高。

激光技术；盖革模式；时隙；探测概率；测距精度

引 言

近年来，具有单光子探测灵敏度的盖革模式雪崩光电二极管（Geiger mode avalanche photodiode，GM-APD）探测器在极弱光探测领域得到了应用。此类探测器工作在盖革模式下，当探测到一个或多于一个光子时，GM-APD探测器就会发生雪崩效应使输出电流迅速达到饱和值，这个过程通常是瞬态的［1］。GM-APD探测器雪崩增益极高，输出信号可直接驱动后续数字信号处理电路。同时，GM-APD探测器具有全固态结构、高增益、体积小、重量轻、功耗低、工作稳定性好、响应速度快和光谱响应范围宽等优点，因此，近年来国内外学者对基于GM-APD探测器的激光雷达进行了大量研究［1-7］。

激光测距主要有干涉法测距、三角测量法、脉冲测距和相位差法测距，其中利用飞行时间法的脉冲测距常用于远程非合作目标测距，相位差法则适于短程测距［8］。对于基于直接探测体制的脉冲激光雷达，由于回波光子到达时间的随机分布，使探测到的目标距离具有一定的不确定性，这种不确定性限制了激光雷达的测距精度。测距精度是用来评价激光雷达性能优劣的关键参量之一。2009年OH等人［6］对基于GM-APD探测器的激光雷达的距离漂移误差进行了研究。2010年WANG等人［7］研究了GM-APD探测器概率连续分布时测距精度的理论。本文中从激光雷达原理与工作时序出发，利用调Q激光脉冲波形，由长死时间、宽回波脉宽情况下探测概率的分布，对系统的目标探测概率和虚警率进行了研究。由统计原理与质心法，建立了测距精度模型。利用数值方法，分析了回波强度、回波脉宽、噪声和回波位置等参量对系统目标探测概率、虚警率和测距精度的影响，研究结论对后续基于GM-APD探测器的脉冲激光雷达的研制具有一定指导意义。

1 系统原理

基于GM-APD探测器的脉冲激光雷达利用飞行时间法测距，其工作原理如图1所示。

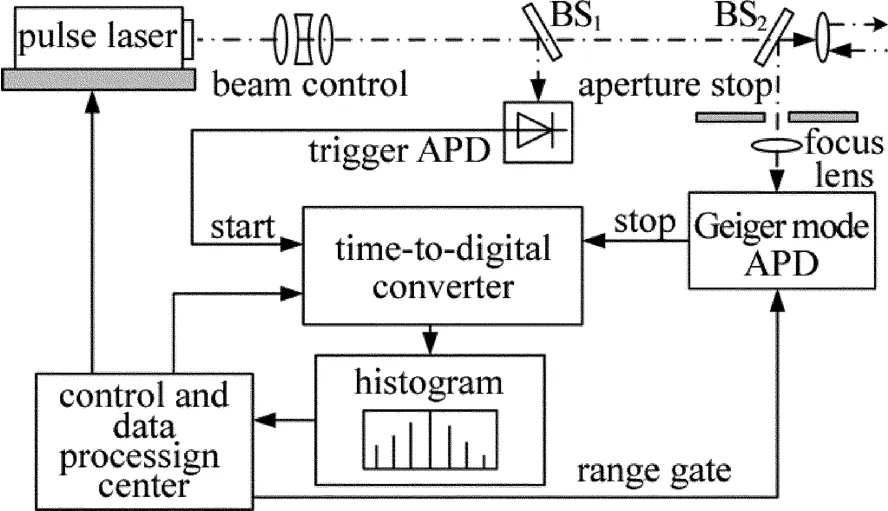
Fig.1 Ranging principle of pulse flight timemethod

激光器发射的短脉冲经分束器BS1，一束射向目标，一束由触发APD接收产生计时开始信号，回波光子触发GM-APD探测器雪崩产生计时停止信号。每一次触发探测会增加一次光子计数操作，经过多脉冲探测即获得到达时间的直方图，通过时间获取算法可获得激光脉冲的飞行时间，即目标距离。

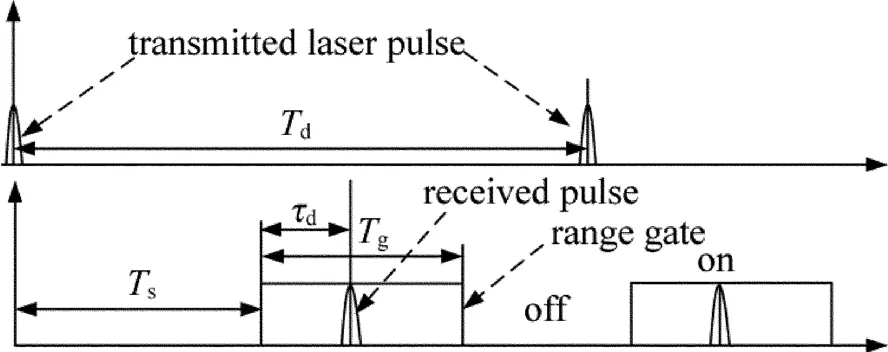
Fig.2 Ranging timing diagram of time-of-flight

在激光雷达中，一般采用距离门技术抑制背景噪声和GM-APD探测器暗计数噪声的影响［9］。采用距离门技术的脉冲激光雷达的工作时序如图2所示，其中，Td是两个发射脉冲间隔，Ts是距离门开始时间，Tg是距离门持续时间，即探测器仅在Tg内才可探测；τd是相对距离门开始位置的回波位置。因距离门外不发生探测，所以可将距离门开始时刻作为相对计时零点。

当加在APD上的反偏电压略高于雪崩击穿电压时，APD工作在盖革模式。GM-APD探测器产生雪崩现象后，若雪崩一直持续，将对GM-APD探测器造成击穿损伤，因此必须对雪崩进行抑制。雪崩抑制电路在GM-APD探测器产生雪崩后可同步产生一个可鉴别输出，使GM-APD探测器两端的偏压快速降到低于雪崩电压以抑制雪崩，在雪崩停止后，再使GM-APD探测器两端的偏压快速恢复到正常工作状态，以便接收下一次光子事件。从抑制雪崩到恢复正常偏压的这段时间，GM-APD探测器不能响应任何光子事件，这段时间称为GM-APD探测器的死时间［10-11］。

在长死时间情况下，死时间与距离门宽度相当，在距离门内探测器只发生一次探测，探测器最多产生一个雪崩脉冲。若为短死时间情况，则每次探测可能产生两个以上的雪崩脉冲。若探测系统的时间数字转换器（time-to-digital converter，TDC）的分辨时间为τb，则距离门内共有q＝Tg／τb个探测时隙。回波脉宽为pw，若脉宽小于TDC分辨时间，则激光能量集中在一个探测时隙里触发，如图3a所示。

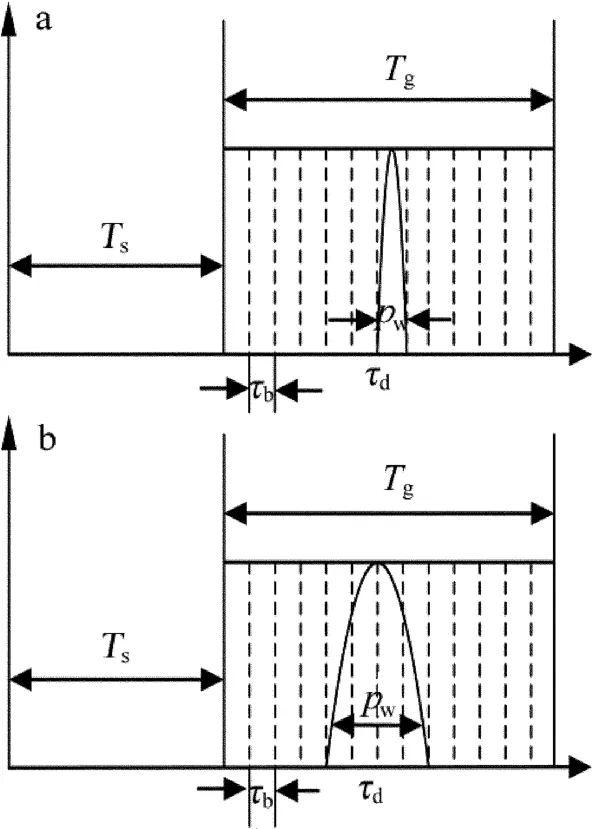
Fig.3 The relation between echo pulse width and resolution time of TDCa—pw≤τb b—pw＞τb

若脉宽大于TDC分辨时间，则脉宽包含的时隙数为r＝pw／τb，对应的时间关系如图3b所示。本文中仅研究长死时间且脉宽大于TDC分辨时间的情况。

2 探测理论

在极弱光探测时，镜面目标回波光子服从Poisson分布，而漫反射目标回波光子服从负二项分布（negative-binomial distribution，NBD）。一般情况下，弱光探测时回波光子数k比激光的模式数参量M小很多，即k／M≪1，此时负二项分布转化为Poisson分布［12-13］。此外，互不相关的背景噪声与暗计数噪声均服从Poisson分布，两种噪声叠加的总噪声仍服从Poisson分布。因此回波光子与噪声均可认为服从Poisson分布。由Poisson分布统计，在t1至t2探测间隔内，产生k个光电事件的概率为：

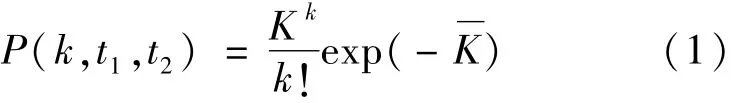
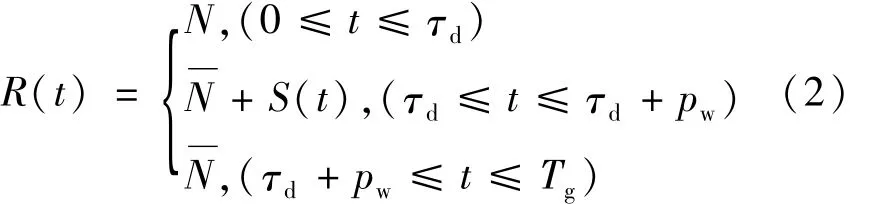
式中，N为平均噪声初始电子数，S（t）为与回波脉冲形状相关的初始电子数分布（即率函数）。在探测间隔［t1，t2］内不发生探测的概率为P（0）＝exp（－K），探测到一个或多于一个初始电子的概率为［14-15］：

由于GM-APD探测器在距离门内只产生一次探测，故其在第j个时隙产生探测的概率是条件概率分布，为前j－1个时隙内没有产生探测的概率与在第j个时隙内发生探测的概率的乘积：

调Q激光脉冲回波信号的率函数为［16］：

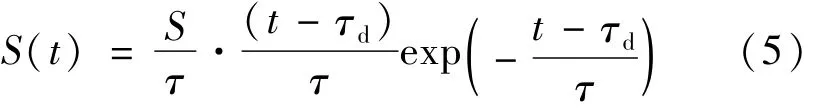
式中，τ＝pw／3.5，S为信号回波脉冲的总初始电子数。则第j个时隙的初始电子数分布为：

若S＝10，τd＝50ns，Tg＝100ns，τb＝0.5ns，pw＝10ns，并设每个时隙的初始电子数分布S（i）为常数，则回波初始电子在探测时隙中的分布如图4所示，这种分布本质上是一种概率分布，显然波峰处回波初始电子出现的可能性更大。

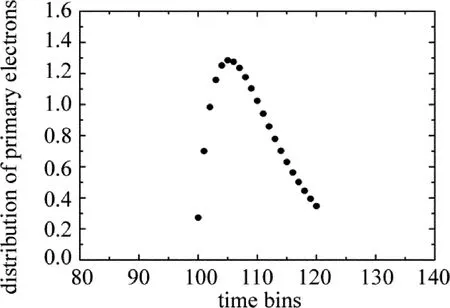
Fig.4 The distribution of primary electrons in detection time bins

为简化分析，设噪声在探测时间内无随机涨落，则落在每个时隙的噪声初始电子数为nb＝Nτb，且回波位置前时隙数为f＝τd／τb，因此第j个时隙的探测概率为：

将（5）式代入（7）式，计算出Pd（j）表达式为：

因此回波激光脉冲的目标探测概率为：

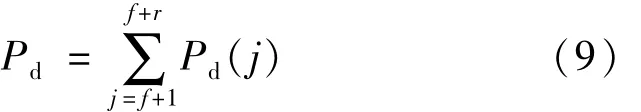
式中，r是S（t）所占据的时隙数。回波激光脉冲的虚警率为［15］：

式中，右边第3项exp（－S－N·Tg）表示信号与噪声存在却不发生探测的概率。

3 探测性能分析

由（5）式～（10）式，对于不同回波脉宽，不同噪声强度时目标探测概率与虚警率的分布如图5所示。为分析噪声与脉宽对目标探测概率和虚警率的影响，将调Q脉冲简化为方波脉冲，则落在每个探测时隙中的信号初始电子数为常数s，目标探测概率为［6］：

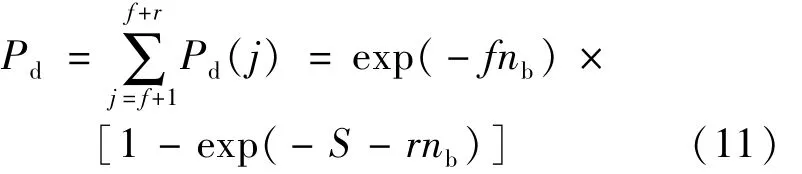
式中，S＝q·s。由（11）式可知，若回波较弱，即S较小时，rnb项的影响不可忽略；脉宽越宽，所占据的探测时隙数越多，rnb越大，此时Pd反而越大。图5显示了该结果，对于τd＝50ns和pw＝40ns，在S＜0.4时，由于落在回波脉宽所占据时隙中噪声的影响，对于越强的噪声，Pd反常变大。但是这种目标探测概率的增加，实质上是由位于目标探测时隙中噪声的作用引起的反常现象，对于脉冲激光雷达，脉宽越宽，系统测距精度越小，因此使用宽脉宽对系统探测性能的改善是没有帮助的。此外，有弱回波时，噪声越强，虚警率越高；但由于噪声的影响不可忽略，宽回波脉宽相比于窄回波脉宽时的虚警率反而更小。

Fig.5 Pdand Pfwith different noise level

回波较强时，噪声越大，目标探测概率越小，虚警率越高。且在S≥10时，探测概率趋于饱和，因此本文中仅在0.1≤S≤10内进行分析［15］。在回波S≤1，且噪声较弱（N—Tg＝0.05）时，因（10）式右边第3项的减幅比第2项增幅要大，故虚警率略有上升；在回波S＞1后，虚警率下降。此外，用来区分强弱回波强度的S由脉宽决定，脉宽越宽，该S越大。因此，噪声越弱，脉宽越窄，系统探测性能越好。

在探测景深内，不同距离的目标，其回波位置也不同。图6所示为不同回波位置对目标探测概率与虚警率的影响。由图可见，回波位置越靠后，f越大，目标探测概率越小，虚警率越大；且τd越小，虚警率下降越快。因此，位于距离门前端的回波位置能获得更好的探测性能。

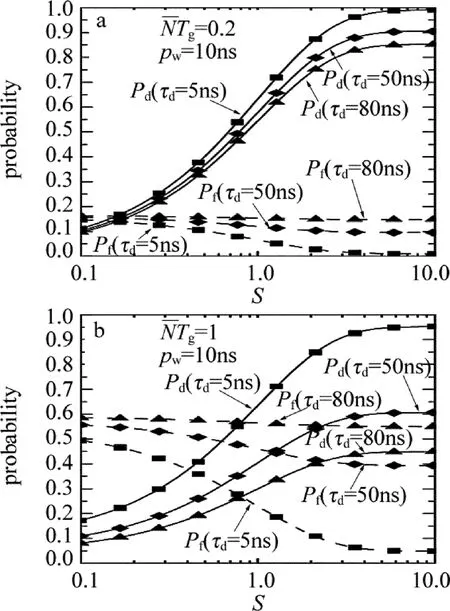
Fig.6 Pdand Pfwith different echo position

4 测距精度分析

4.1 测距精度模型

根据统计原理与质心法，回波光子到达时间均值可表示为：

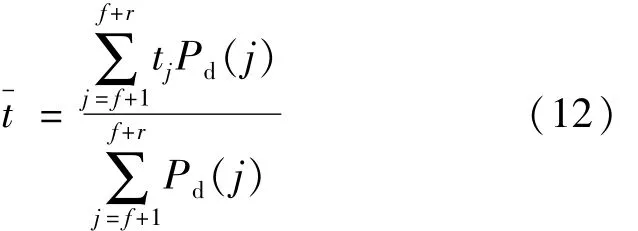
式中，tj＝j·τb是回波光子激发探测的时隙的时间位置。在获得回波的时间均值后，将其与真实回波时间位置的差乘以光速即得系统测距精度。时间均值与真实目标时间的差越小，探测距离与目标真实距离越接近，测距精度越高，测距精度可写为：

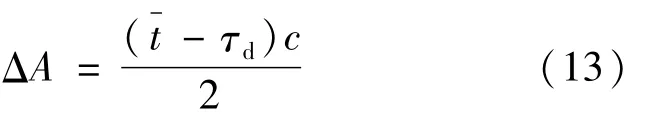
式中，c为光速。回波脉冲飞行时间的方差可表示为：

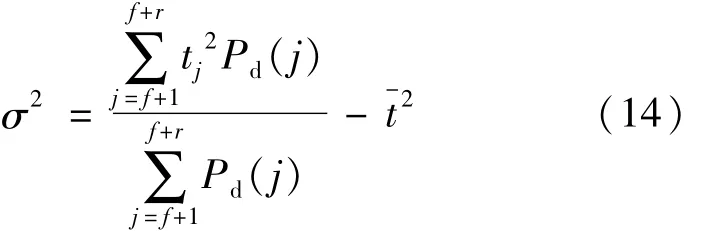
回波信号的方差代表了探测值与均值的离散程度，方差的平方根定义为标准偏差，标准偏差可以用来表征探测数据的精确度，飞行时间的标准差乘以光速得到距离标准差为：

4.2 结果与讨论

由前述分析可知，影响飞行时间均值、测距精度与标准差的因素有回波强度、回波脉冲宽度、背景噪声与暗计数噪声。由图7～图9可知，回波信号强度越强，激发的初始电子数越多，因此目标探测概率越高，时间均值越接近真实时间，测距精度就越高，距离标准差越小，探测距离越接近真实距离，探测数据的一致性越好，探测距离的精确度越高。

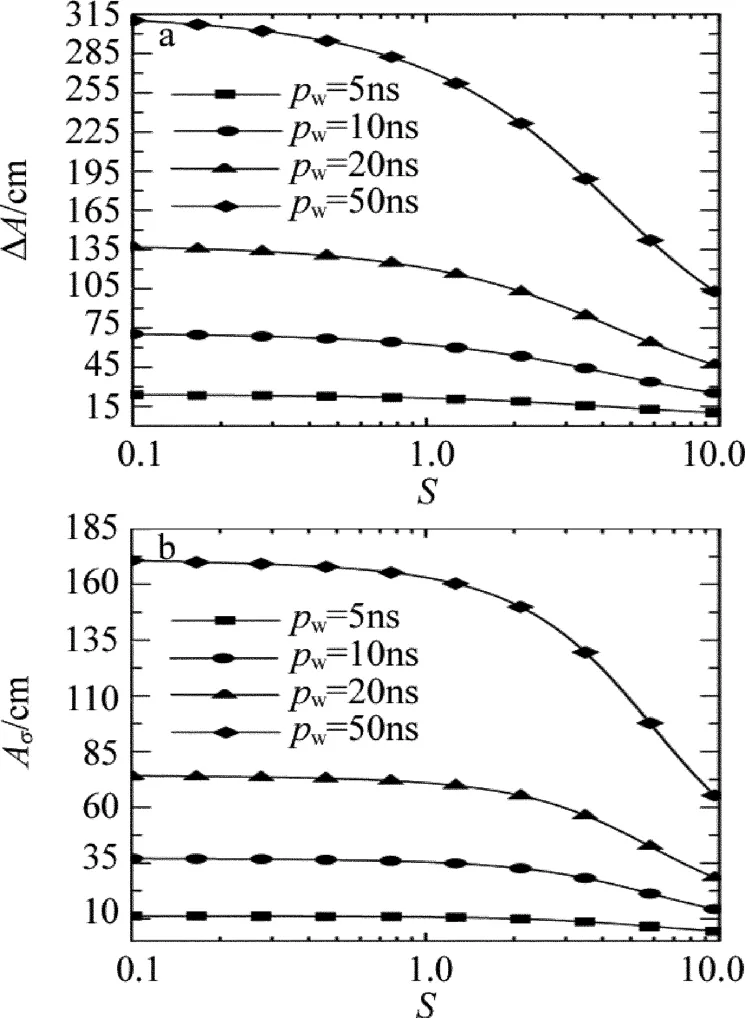
Fig.7 The influence of echo pulse width on the ranging accuracy and the standard deviation of distance

Fig.8 The influence of noise on the ranging accuracy and the standard deviation of distance

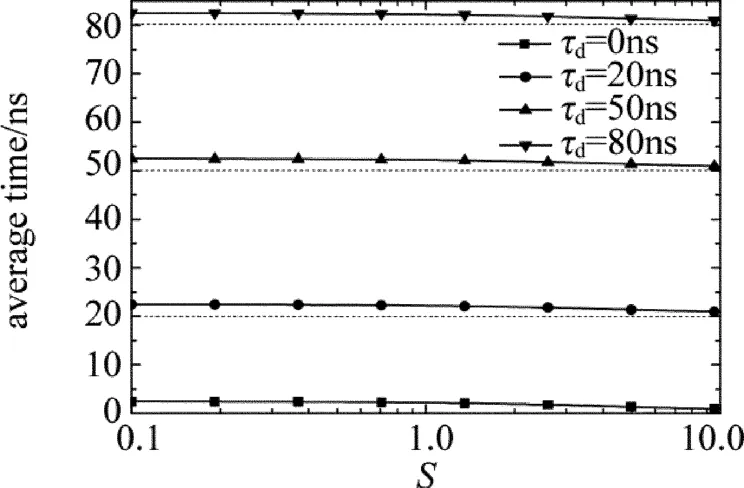
Fig.9 Average arrival time with different echo position

回波脉宽是影响测距精度的另一重要参量，回波脉宽对测距精度和标准差的影响如图7所示。由图可见，由于回波光子不可能出现在脉冲之外，脉宽越窄，光子能量更为集中，则光子的时间分布处在更小范围，因此测距精度越高，距离标准差越小。弱回波强度时，脉宽对测距精度的影响比强回波强度时大，但若采用脉宽为5ns的窄脉冲，噪声强度为50kHz时，即使在极弱回波强度下，仍可获得低于30cm的测距精度；在回波初始电子数多于6时，可得低于10cm的测距精度；信号初始电子数为10时，可达8cm左右的测距精度。这些结论与参考文献［6］和参考文献［7］中的研究结果符合得很好，测距精度的变化规律与本文中研究结果一致，参考文献［7］中主要是对测距精度的变化规律作了理论研究，采用的是连续概率分布模型，相当于本文中TDC分辨时间趋于0时的结果。同时，在参考文献［6］中，当目标距离为8m时，利用其设计参量，得到最强回波（S＝10）和最弱回波（S＝0.1）的距离漂移误差不超过18cm，且随着回波强度的增加，这种距离漂移误差变小。本文中采用的设计参量与参考文献［6］中的不完全相同，测距精度模型的参考时间是回波脉冲理想到达时间τd，而不是以参考文献［6］中S＝10时的平均到达时间，但计算所得测距精度变化规律与参考文献［6］中的试验结果符合得比较好。因此，更强的回波强度，更窄的回波脉宽，将获得更好的系统测距精度。

系统使用的距离门只能抑制噪声但不能完全消除噪声，噪声是虚警率的主要来源，噪声对测距精度和距离标准差的影响如图8所示。在弱回波强度时，由于GM-APD探测器被噪声触发的概率增加，因此噪声对测距精度的影响很大，探测数据较为分散，且噪声越强，测距精度越小。由于距离门对噪声的抑制作用，当回波初始电子数大于1时，GM-APD探测器被回波光子激发的概率增加，噪声的影响减小，故不同噪声对测距精度的影响趋于一致，距离标准差变化也相同。

在探测景深范围内，对于不同距离的目标，距离门内的回波位置是不同的，一般情况下噪声均匀分布在距离门内，因此GM-APD探测器也可能被回波位置前的噪声触发探测。但距离门一般不是很宽，落入其内每个时隙的噪声初始电子数很少，因此回波脉冲位置对测距精度影响很小。不同目标回波位置测距时间均值如图9所示。可见，回波位置在弱回波强度时对测距精度的影响稍大，当回波信号强度增加，回波时间均值趋近于τd，即测距精度越高。

5 结 论

根据回波信号初始电子的概率分布，对基于GM-APD探测器的激光雷达的探测性能和测距精度进行了研究。结果表明，回波越强，探测概率越高，虚警率越小，系统测距精度越高，距离标准差越小，系统探测性能越好。脉宽越窄，回波能量更为集中，因此，使用窄脉宽能获得更好的探测性能、更高的测距精度与更小的距离标准差。噪声是影响系统性能的另一重要因素，噪声越强，目标探测概率越低，虚警率越高，但由于噪声被距离门所抑制，故噪声仅在弱回波强度时对测距精度与距离标准差的影响较大。回波位置对测距精度的影响本质上与噪声的影响一样，回波位置越靠前，噪声影响越小，系统探测性能越好，但根据测距精度模型，当使用的距离门较窄时，噪声对每个探测时隙的影响较小，因此不同回波位置对测距精度的影响不明显。此外，采用脉宽为5ns的窄脉冲，即可获得低于10cm的测距精度，可见GM-APD探测器在远程极弱回波探测领域具有巨大优势，完全可应用于高分辨率3维成像激光雷达中。

［1］ AULL B F，LOOMISA H，YOUNG D J，et al.Geiger-mode avalanche photodiodes for three-dimensional imaging［J］.Lincoln Laboratory Journal，2002，13（2）：335-350.

［2］ JIANG L A，LUU JX.Heterodyne detection with aweak local oscillator［J］.Applied Optics，2008，47（10）：1486-1503.

［3］ ALBOTA M A，HEINRICHSR M，KOCHER D G，et al.Threedimensional imaging laser radar with a photon-counting avalanche photodiode array and microchip laser［J］.Applied Optics，2002，41（36）：7671-7678.

［4］ NICLASSC，ITO K，SOGA M，et al.Design and characterization of a 256×64pixel single-photon imager in CMOS for a MEMS-based laser scanning time-of-flight sensor［J］.Optics Express，2012，20（11）：11863-11881.

［5］ ITZLER M A，ENTWISTLE M，OWENSM，et al.Geiger-mode avalanche photodiode focal plane arrays for three-dimensional imaging LADAR［J］.Proceedings of SPIE，2010，7808：78080C.

［6］ OH M S，KONG H J，KIM T H，et al.Reduction of range walk error in direct detection laser radar using a Geigermode avalanche photodiode［J］.Optics Communication，2010，283（2）：304-308.

［7］ WANG F，ZHAO Y，ZHANG Y，etal.Range accuracy limitation of pulse ranging systems based on Geiger mode single-photon detectors［J］.Applied Optics，2010，49（29）：5561-5566.

［8］ GAO Y Y，LIY H，FENG Q L，et al.Optical design of a laser distancemeasuring system based on high frequency digital phase detection［J］.Laser Technology，2013，37（3）：353-356（in Chinese）.

［9］ BONNIER D，LAROCHELLE V.A range-gated imaging system for search and rescue，and surveillance operations［J］.Proceedings of SPIE，1996，2744：134-145.

［10］ GATT P，JOHNSON S，NICHOLS T.Dead-time effects on geiger-mode APD performance［J］.Proceedings of SPIE，2007，6550：65500l.

［11］ STIPCEVICM.Active quenching circuit for single-photon detection with Geigermode avalanche photodiodes［J］.Applied Optics，2009，48（9）：1705-1714.

［12］ GOODMAN JW.Some effects of target-induced scintillation on optical radar performance［J］.IEEE，1965，53（11）：1688-1700.

［13］ GOODMAN JW.Statistical optics［M］.New York，USA：Wiley-Interscience，1985：475-480.

［14］ HENRIKSSON M.Detection probabilities for photon-counting avalanche photodiodes applied to a laser radar system［J］.Applied Optics，2005，44（24）：5140-5147.

［15］ FOUCHE D G.Detection and false-alarm probabilities for laser radars that use Geiger-mode detectors［J］.Applied Optics，2003，42（27）：5388-5398.

［16］ STEINVALL O，CHEVALIER T.Range accuracy and resolution for laser radars［J］.Proceedings of SPIE，2005，5988：598808.

Theoretical analysis of detection performance and range accuracy of photon ladar

LUO Hanjun，ZHOU Renlong，ZHANG Yutao
（School of Physics and Electronic Science，Hunan University of Science and Technology，Xiangtan 411201，China）

In order to investigate the detection performance and range accuracy of a laser radar using Geiger mode avalanche photodiode（GM-APD）as detector，by using themethod ofmathematicalmodeling，based on the system working principle and detection time sequence，the target detection probability was analyzed under the condition that the GM-APD detector operated under long dead-time and the echo pulse width was larger than the resolving time of the time-to-digital converter（TDC）.According to the statistical theory and centroid method，the theoretical model of range accuracy was established.Using the system design parameters，the influence of the echo intensity，pulsewidth，noise，and echo position on the range accuracy was discussed.The results show that the stronger echo intensity，the narrower echo pulse width，the lower noise and themore front echo position result in the higher target detection probability，the lower false alarm rate and the better detection performance.Echo intensity and pulse width are themain influence factors.The stronger echo intensity and the narrower pulse width result in the higher range accuracy.

laser technique；Geigermode；time bin；detection probability；range accuracy

TN958.98

A

10.7510／jgjs.issn.1001-3806.2014.03.028

1001-3806（2014）03-0411-06

国家自然科学基金资助项目（11247003）

罗韩君（1975-），男，博士，讲师，现主要从事单光子成像探测方面的研究。

E-mail：393593928＠qq.com

2013-07-09；

2013-07-30