参数率定方案对水温数值模拟结果的影响

刘 肖,陈青生,魏小旺

(1.河海大学 水利水电学院,江苏 南京 210098;2.浙江省钱塘江管理局勘测设计院,浙江 杭州 310016)

参数率定方案对水温数值模拟结果的影响

刘 肖1,陈青生1,魏小旺2

(1.河海大学 水利水电学院,江苏 南京 210098;2.浙江省钱塘江管理局勘测设计院,浙江 杭州 310016)

建立了立面二维水动力-水温模型,运用建库前天然河道及邻近区域同类型水库两组不同实测资料对模型进行参数率定。根据这两组计算参数分别模拟了验证时段内D水库水温分布,以及A水库库区水温变化过程。数值模拟结果表明,在其他条件保持一致的情况下,天然河道及邻近区域同类型水库资料均可用于数值模拟参数的率定,将两组验证参数用于实际计算时,所得结果表现出相同的规律,但具体数值存在一定差异。分析认为,邻近区域同类型水库资料验证更符合实际情况,故在此类水库水温的数值模拟中,应尽量选择邻近区域同类型水库资料作为验证资料,若在条件不足的情况下,相关的天然河道资料也可以作为参考。

参数率定;水库水温;数值模拟

大型水库建成后,库区内水深增加,水体流速减小,水体热量输运过程随之发生变化,使得水温分布结构发生变化,库区水温分布及下泄水体的水温不同于天然河道,对下游的水环境会产生一定影响[1-2]。因此,国内外学者对模拟及预测水库水温进行了大量的研究。张士杰等[3]总结了我国水库水温研究现状及存在问题,并提出了今后的发展趋势;胡平等[4]介绍了目前工程中预测水库水温分布的主要方法,并采用水库水温数值分析软件,对二滩水库和锦屏一级水库水温进行数值预测。数值模拟方法是预测水温的一种常用方法,而对所建数学模型的参数率定是数值模拟过程中很重要的一个步骤,参数的选择是否合适,直接关系到计算结果的准确性和可靠性[5-9]。然而,水温预测研究工作一般是在水库尚未建成前进行,往往难以获得水库实测资料,一般可以采用邻近区域同类型水库或者天然河道的相关实测资料对模型参数进行率定。目前对两种模型参数的率定方式的对比分析研究较少。本文以西北地区某A水库为例,采用立面二维水动力-水温数学模型[10-11],利用天然河道水温(方案1)及邻近区域D水库水温(方案2)两种不同的验证方案对模型分别进行了验证,经过参数率定,得到两组不同的模型计算参数,在保证其他条件一致的情况下利用这两组计算参数模拟计算A水库水温,并对数值计算结果进行了对比分析。

1 水库水温数学模型的建立

水库水温分层主要发生在垂向,水面风速、风向作为影响水体热交换重要因素,其分布在河道纵向上需要加以考虑,结合水库规模(坝前水深、水面面积、水面宽度和回水长度等)及调节性能,对于本文所研究的狭长型水库确定采用沿横向积分的立面二维的水动力水温数学模型。立面二维水动力-水温数学模型主要控制方程如下,方程定义河道走向为x轴,垂向垂直于河道为z轴,横向垂直于河道为y轴。

连续方程:

动量方程:

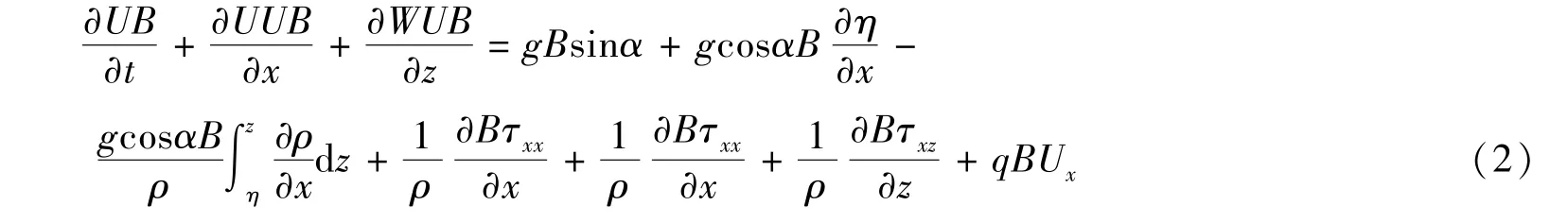
式中:Tw为水温;U,W为流速在水平方向和垂直方向上的分量;B为水面在y方向上的宽度;P为压力;g为重力加速度;子x,子z为x方向和z方向上的切应力;ρ为密度;η为水位;α为底坡;Ux为支流流速的x分量; q为单位宽度上的流量;qΦ为每单位体积横向入流/出流中的温度或组分质量流量;Φ为温度或组分浓度, Dx为纵向温度或组分分散系数,Dz为垂向温度或组分分散系数;SΦ为横向平均的源/汇项(本文计算中无横向入流/出流及源/汇项,故取值为0)。

上游入流边界给定逐月来流流量、水温,出流边界给定水库逐月下泄流量;水气交界面给定月平均气温、风速风向、云量等。

初始条件分两次设定,首次计算初始条件给定计算起始时刻水位,初始温度分布为计算起始时刻平均来流水温,经一个完整周期的计算得到稳定结果后,采用首次计算的结束时刻结果作为正式计算的初始条件。

本文选用有限差分法对控制方程进行离散求解,得出式(1)～(6)中的U,W,TW,P,ρ和η共6个变量。采用交错网格系统解决压力梯度和连续方程[6]的离散困难。

2 模型验证

模型验证的目的主要在于校核相关气象条件与计算参数的选择是否恰当,能否满足计算需要。根据现有实测资料,本文模型验证分为方案1水温验证和方案2水温验证2个步骤进行,其中方案1还包括水面线的验证。

2.1 方案1水温验证

根据A水库坝址、库区河段大断面及实测水面线资料进行水面线验证。选择A水库的天然河道作为水面线验证的计算验证区域,该区域河道长11.9 km,落差123.8 m。

图1 A库区水面线验证Fig.1 Verification of the flow profile in Reservoir A

根据选定的计算区域对网格进行划分,从30 m精度DEM地形图上确定该河段的走势,以便更好地模拟实际河道水流状态,主流方向的网格节点根据实测河道深泓点位置来布置,尺度为15～228 m,垂向网格尺度均为1 m。根据实测水位与河道断面资料由谢才公式反推来流流量,求得Q=360 m3/s,以此作为入流流量,下游边界设为水位边界,通过调整河道糙率使得计算值与实测值基本吻合,验证结果如图1所示。

由图1可知,计算值与实测值二者基本吻合,表明各项水动力参数及条件选择恰当,所建立数学模型可以准确模拟该河段的水动力计算。

以水面线验证为基础进行水温验证。通过该河道上游S1及下游S2两个水文站某年同一日期所测水温值的分析比较,可以得出逐月的单位千米温升值。由于A水库库区纵向长度仅为12 km,河段温升不显著,故根据所给库区中的30个实测地形断面资料,概化出一个平均断面,以此为基础,按照此段河道的河道底坡,向上下游分别对计算区域进行了一定长度的延伸,得到25 km的概化河道,为排除上下游边界对河道水温的影响,取该段河道中间的20 km为有效计算区域进行分析。计算区域沿主流方向网格尺度为200 m,垂向尺度为0.4 m。入流条件采用S2水文站该年逐日实测流量资料,上游边界给定S2水文站实测天然水温,并给定气温、风速风向、云量等气象资料,计算结果如图2所示。可见,计算最大误差为4%左右,计算值与实测值基本吻合,表明各项参数及条件选择恰当,所建立数学模型可以用于水温预测分析。

2.2 方案2水温验证

根据现有实测地形及水文资料,对下游D水库坝前垂向水温进行模拟验证。

D水库位于A水库下游16 km处,坝高110 m,坝顶高程1 654 m,正常蓄水位1 646 m,正常蓄水位下总库容1.25亿m3。根据国际科学数据服务平台提供的30 m精度DEM地形图,对D水库建模,沿河道方向网格尺度为100 m,网格数为122,垂向网格尺度为1 m,网格数为103。计算时采用的边界条件见图3。

通过模拟计算,对相关参数进行率定,得到D水库6月3日(典型年)坝前垂向水温分布,计算水温与实测水温的比较见图4,可见,计算结果与实测值吻合良好。

图2 水温验证Fig.2 Verification of the water temperature

图3 D水库入流出流过程及气温和水温分布Fig.3 Inflow and outflow,air temperature and inflow temperature of Reservoir D

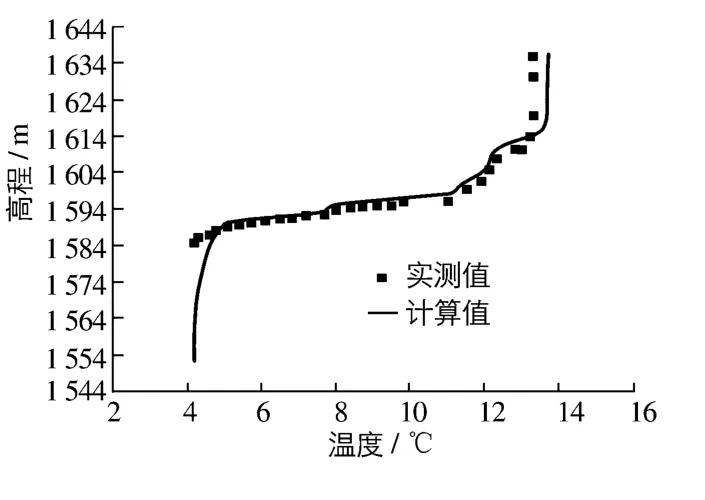
图4 D水库6月3日坝前水温验证Fig.4 Water temperature verification of Reservoir D in front of the dam

3 数值模拟结果及分析

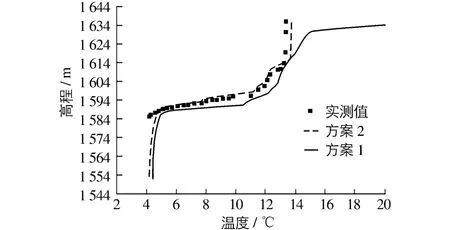
图5 两种方案下D水库6月3日坝前水温对比Fig.5 Water temperature comparison in front of the dam under two schemes

3.1 运用两组方案分别模拟D水库水温

为比较两组参数对水库水温数值模拟的影响,首先采用方案1(天然河道)率定好的参数对D水库水温进行了数值模拟,计算中其他初始条件、边界条件、计算时段与方案2保持一致。图5给出了同一时间节点上的数值模拟结果。从图5可以看出,由方案2验证资料得到的计算模型参数对D水库的水温模拟与实测值拟合程度较好,而由方案1得到的D水库的水温模拟与实测值有一定的偏差,其偏差在水库上层尤为明显,与实测资料相比,方案2表层水温相差约0.5℃,而方案1表层水温与实测值相差约6.5℃。另一方面,两种方案计算结果在水库中下层均与实测结果相近,且库区水温垂向分布呈现相同的规律,存在明显的水库分层结构,表温层、温跃层、低温层高度基本一致。

可见,由于水库建成后,与天然河道相比,水动力条件明显改变,水深增加亦使得底部边界热动力条件发生变化,故而采用方案1(天然河道)率定的参数用于水库水温计算时,应用条件存在明显差异,导致计算结果偏差较大,且偏差主要体现在水库表层。故采用邻近区域水库实测资料作为模型验证资料更为合理,其结果准确性与可靠性更高。

3.2 模拟A水库库区及下泄水温

A水库正常蓄水位为1 820 m,正常蓄水位下总库容约2.19亿m3。以A水库实测地形资料及枢纽特性为基础,构造计算区域的网格,主流方向的网格节点根据实测河道深泓点的位置来布置,尺度为15～228 m,垂向网格尺度均为1 m。另外从30 m精度DEM地形图上确定该河段的走势情况,以便更好地模拟水库水温分布情况。

根据S2水文站实测水温利用沿程增温率法推算A水库库尾的逐月水温值作为A水库的入库水温,模拟计算A水库平水年(P=50%)正常蓄水位1 820 m下的水库水温分布及下泄水温过程,A水库上层水温及电站引水口温度计算结果如图6所示。由图6可见,两组不同参数下的上、下层水体及电站引水口温度变化规律一致,12月,1月,2月处于冬季,气温低于0℃,水面会出现结冰现象,河道及水库上层温度接近0℃。在其他月份,由于水库内水流流动较天然状态下变缓,而相应的气温值高于水温值,故水库上层水体的温升比天然河道条件下大,水库表层温度高于天然河道的水温。由此可知,两组不同参数对A水库库区及下泄水温的计算结果遵循同样的变化规律,但在结果上存在一定差别。

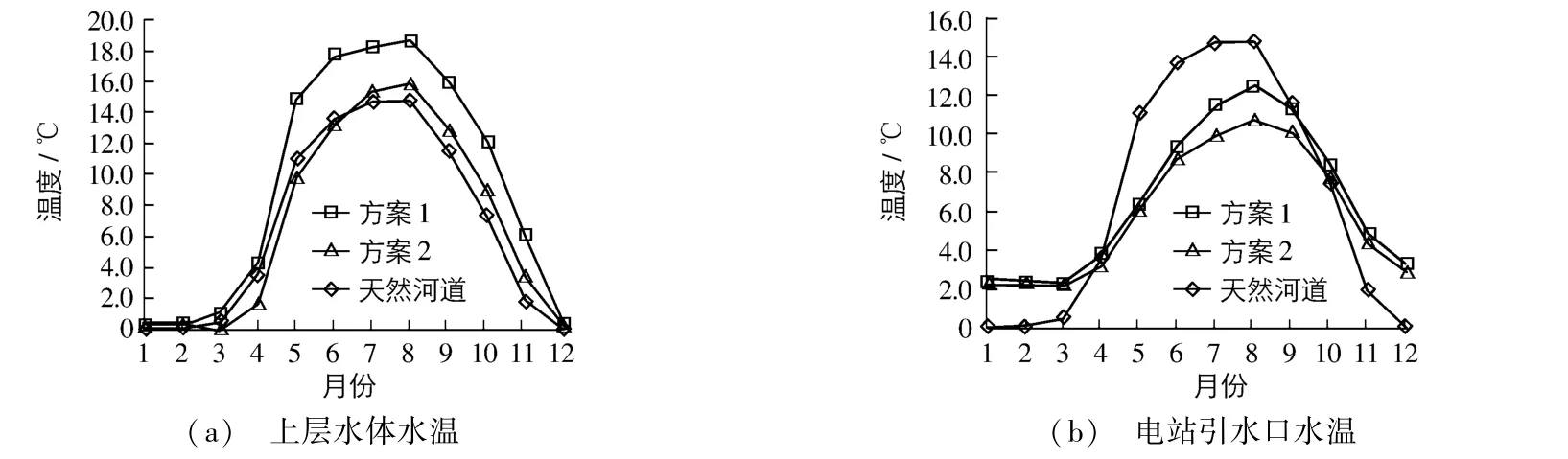
图6 上层水体及电站引水口水温对比Fig.6 Comparison between the water temperature of upper water body and that of intake of hydropower station

4 结 语

本文建立了立面二维水动力-水温模型,运用建库前天然河道及邻近区域同类型水库两组不同实测资料对模型进行参数率定。根据这两组计算参数分别模拟了验证时段内D水库库区水温分布,以及A水库库区水温变化完整过程,得出以下结论:

(1)由方案2(邻近水库)验证资料得到的计算模型参数对D水库的水温模拟与实测值拟合程度较好;而由方案1(天然河道)得到的D水库的水温模拟与实测值有一定的偏差,其偏差在水库上层尤为明显。

(2)两种方案计算结果在水库中下层均与实测结果相近,且库区水温垂向分布呈现相同的规律,存在明显的水库分层结构,表温层、温跃层、低温层高度基本一致。对A水库的完整水温变化过程数值模拟结果表明,两种方案对A水库库区及下泄水温的计算结果遵循同样的变化规律,但在数值上稍有不同。

(3)在其他条件保持一致的情况下,天然河道及邻近区域同类型水库资料均可用于数值模拟参数的率定,邻近区域同类型水库资料验证更符合实际情况,故在此类水库水温的数值模拟中,应尽量选择邻近区域同类型水库资料作为验证资料,若在条件不足的情况下,相关的天然河道资料也可以作为参考,仍能反映出水温变化的大致规律。

[1]蔡为武.水库及下游河道的水温分析[J].水利水电科技进展,2001,21(5):20-23.(CAI Wei-wu.Analysis of water temperature of reservoir and downstream river[J].Advances in Science and Technology of Water Resources,2001,21(5):20-23.(in Chinese))

[2]薛联芳,顾洪宾,崔磊,等.红水河干流梯级开发对水温累积影响的调查研究[J].水力发电,2010,36(11):5-8. (XUE Lian-fang,GU Hong-bin,CUI Lei,et al.Study on cumulative effects to water temperature caused by the hydropower cascade development in Hongshui River[J].Water Power,2010,36(11):5-8.(in Chinese))

[3]张士杰,刘昌明,王红瑞,等.水库水温研究现状及发展趋势[J].北京师范大学学报:自然科学版,2011,47(3):316-320.(ZHANG Shi-jie,LIU Chang-ming,WANG Hong-rui,et al.A review on water temperature of reservoirs[J].Journal of Beijing Normal University(Natural Science Edition),2011,47(3):316-320.(in Chinese))

[4]胡平,刘毅,唐忠敏,等.水库水温数值预测方法[J].水利学报,2010,41(9):1045-1053.(HU Ping,LIU Yi,TANG Zhong-min,et al.Numerical prediction of water temperature in reservoir[J].Journal of Hydraulic Engineering,2010,41(9): 1045-1053.(in Chinese))

[5]董壮,罗龙洪,郑福寿.岔管流动的数值模拟[J].河海大学学报:自然科学版,2007,35(1):15-17.(DONG Zhuang, LUO Long-hong,ZHENG Fu-shou.Numerical simulation of flow in bifurcated pipes[J].Journal of Hohai University(Natural Science),2007,35(1):15-17.(in Chinese))

[6]潘俊,高维春,田海龙,等.潜流式人工湿地的数值模拟与参数率定[J].水利学报,2010,41(11):1280-1285.(PAN Jun,GAO Wei-chun,TIAN Hai-long,et al.Numerical simulation and parameter calibration for subsurface flow wetland[J]. Journal of Hydraulic Engineering,2010,41(11):1280-1285.(in Chinese))

[7]董壮.三维水流数值模拟研究进展[J].水利水运工程学报,2002(3):66-73.(DONG Zhuang.Advances in 3D flow numerical simulation[J].Hydro-Science and Engineering,2002(3):66-73.(in Chinese))

[8]SHANKAR N J,CHAN E S,ZHANG Q Y.Three dimensional simulation for an open channel flow with a constriction[J]. Journal of Hydraulic Reserach,2001,39(2):187-201.

[9]FISCHER A T,STOESSER T,BATES P,et al.3D numerical modelling of open channel flow with submerged vegetation[J]. Journal of Hydraulic Reserach,2001,39(3):303-310.

[10]郝红升,李克锋,梁瑞峰,等.支流影响下的水库水温预测模型[J].水利水电科技进展,2006,26(5):7-9.(HAO Hong-sheng,LI Ke-feng,LIANG Rui-feng,et al.Water temperature prediction model for the reservoirs under the influence of branches[J].Advances in Science and Technology of Water Resources,2006,26(5):7-9.(in Chinese))

[11]王冠,韩龙喜,常文婷.基于立面二维水动力-水温耦合模型的水库水温分布[J].水资源保护,2009,25(2):59-63. (WANG Guan,HAN Long-xi,CHANG Wen-ting.Modeling water temperature distribution in reservoirs with 2D laterally averaged flow-temperature coupled model[J].Water Resources Protection,2009,25(2):59-63.(in Chinese))

Effects of parameter calibration schemes on numerical simulation results of water temperature

LIU Xiao1,CHEN Qing-sheng1,WEI Xiao-wang2
(1.College of Water Conservancy and Hydropower,Hohai University,Nanjing 210098,China;2.Surveying and Design Institute of Qiantang River Administration of Zhejiang Province,Hangzhou 310016,China)

A vertical two dimensional hydrodynamic-temperature model is established for calculating variation in water temperature in reservoirs.The parameter calibration is carried out by comparing two sets of the observation data from the natural channel and the same types of reservoirs located nearby.According to the two sets of calibrated parameters,the water temperature in Reservoir D during the verification period and the complete process of the water temperature distribution in Reservoir A have been simulated respectively.The numerically simulated results indicate that the data from natural channels and the same types of the reservoirs located nearby can be used in the model parameter calibration when the other conditions remain the same.The numerically simulated results show the same tendency but different values applying those two sets of calibrated parameters.It is confirmed that the parameters obtained from the nearby reservoirs are more reasonable and close to realities.Therefore,it is recommended that in the reservoir water temperature simulation,the data from the same types of reservoirs located nearby are preferred,and the data from the natural channels can be used as a reference for analysis and studies of variation in the reservoir water temperature when the data are insufficient.

parameter calibration;reservoir water temperature;numerical simulation

TV697.2+1

A

1009-640X(2014)04-0082-05

2013-12-09

刘 肖(1988-),女,湖南岳阳人,硕士研究生,主要从事工程水力学研究。E-mail:liuxiao_1224@163.com