无限深透水坝基上悬挂式防渗墙控渗试验研究

毛海涛,何华祥,邵东国,王晓菊

(1.重庆三峡学院 土木工程学院,重庆 404100;2.武汉大学 水利水电学院,湖北 武汉 430072;3.重庆三峡水利电力集团股份有限公司,重庆 404100)

无限深透水坝基上悬挂式防渗墙控渗试验研究

毛海涛1,2,3,何华祥3,邵东国1,王晓菊1

(1.重庆三峡学院 土木工程学院,重庆 404100;2.武汉大学 水利水电学院,湖北 武汉 430072;3.重庆三峡水利电力集团股份有限公司,重庆 404100)

无限深透水地基上巨厚覆盖层的渗流控制是大坝建设成败的关键问题之一。悬挂式防渗墙已在许多此类工程中使用,但其控渗效果和渗流机理的分析研究仍未达成共识。为了进一步研究悬挂式防渗墙的渗流机理和控渗效果,应用无限单元和有限单元结合法来模拟无限深透水地基,分析不同渗透系数、防渗墙深度和水头差时坝基渗流量和渗透坡降的变化规律,拟合出精度较高计算式,并通过渗流槽模型试验进行了验证。分析研究发现,悬挂式防渗墙在控制无限深透水地基渗透坡降方面效果明显,能有效遏制渗透破坏;在控制渗流量方面,悬挂式防渗墙深度越大效果越明显,但需要辅助措施联合控制才能实现经济合理、技术可行的目标。分析研究结果有利于进一步认清悬挂式防渗墙的控渗规律。

无限深透水坝基;渗流;土石坝;悬挂式防渗墙;无限单元法和有限单元法;渗透坡降

随着水电工程的进一步开发,良好坝址越来越少。我国西北及西南地区水坝建设常遇到无限深透水地基问题,而且还有进一步严重的趋势[1]。针对“无限深透水坝基”的巨厚覆盖层,采用悬挂式防渗墙(以下简称悬墙)控制渗流存在两种不同观点。观点一认为:悬墙深度越大,对坝基防渗越有利。理由是随着防渗墙深度增加,渗径相应延长,被保护土(覆盖层)中的平均坡降减小,有利于覆盖层的渗透稳定[2]。观点二认为:随着悬墙深度增加,悬墙底部渗透坡降增大,防渗能力增强。理由是随着成墙深度增加,悬墙上下游承担的水头差增加,悬墙底部坡降增加[3]。若遵循观点一,悬墙达到一定深度后,能够保证渗透流量和渗透坡降在允许范围内即可,不一定要封闭覆盖层。如果将防渗墙做到更深,只会对防渗有利,不会出现危险。按照观点二,防渗墙深度应控制在一定范围,不能太深,否则在防渗墙底部可能出现局部渗透破坏。

本文通过无限元和有限元的耦合建立数值模型,针对无限深透水坝基采用悬墙进行渗流计算。通过公式拟合、试验验证、对比分析对悬墙的控渗规律作进一步研究。

1 无限元数值计算模型

1.1 渗流无限元原理

无限元在概念上是有限元的延伸,是一种几何上可以趋于无限远处的单元[3-5]。广义地讲,无限元仍然属于有限元的范畴,因而它与有限元方法的“协调”与生俱在,比边界元等其他求解无界域问题的数值方法更具有优势[6]。

无限元渗流的拉普拉斯微分方程定义的边界问题转化为等效变分问题:

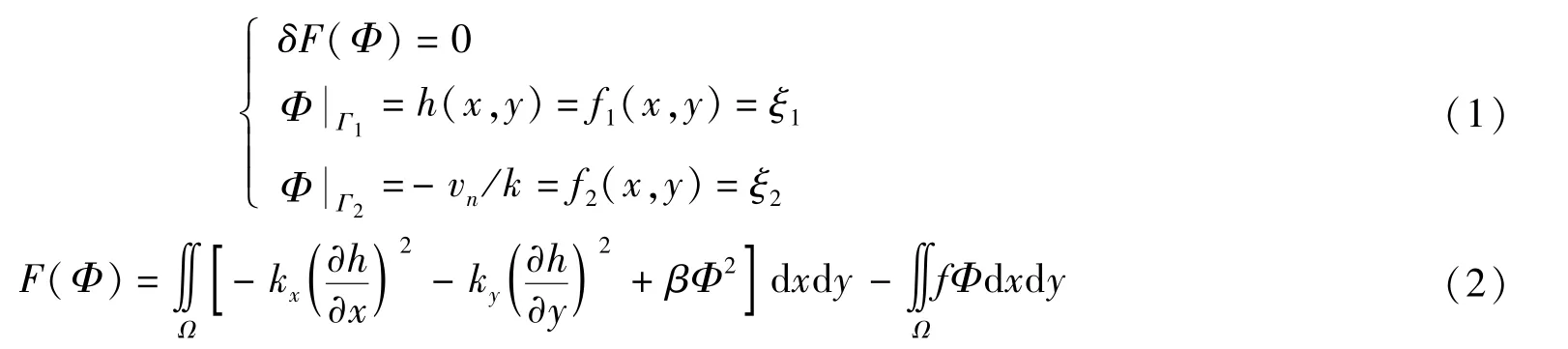
将渗流计算区域分成m个正方形单元,第e单元内任意一点渗流势函数值可以表示为:

式中:上标e为单元全局编码,下标i为节点局部编码,n为单元节点个数,这里选择n=4;f为边界条件函数,Φ为势函数。式中Ni为基函数,满足下式:

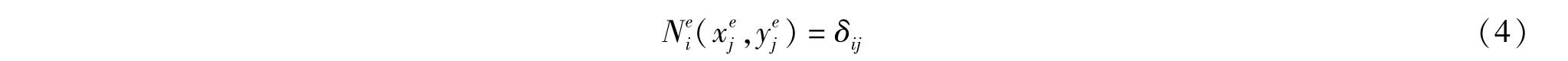
将式(2)离散化后得到

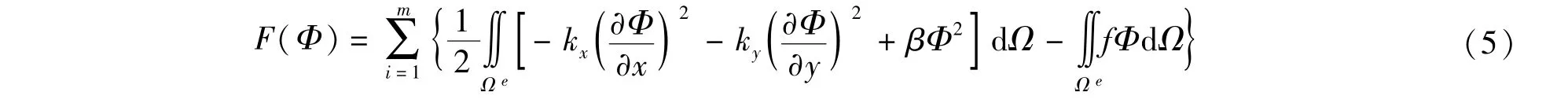
将式(5)代入式(3)对φe进行求导并写成矩阵形式为:

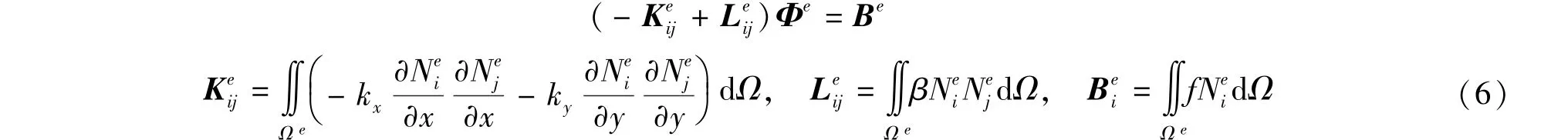
从上述推导过程可以看出,无限元和有限元渗流原理在函数形式、泛函离散和最终矩阵的基本形式相同。因此,二者完全可以结合使用解决无限域渗流问题。

有限单元和无限单元均可以是4结点单元,这给有限元软件的程序开发和技术实现上带来便捷[7],无限单元形成的单元矩阵同样按照整体结点号组装到系统系数矩阵当中,形成最终的稀疏对称复系数方程组。

1.2 数值模型

数值模型采用有限元和无限元结合方法,在大坝坝踵和坝趾前后各200 m和悬墙深度3～5倍的深度区域采用有限单元剖分,在有限单元边界采用无限单元,无限单元在左右和底部趋于无穷远处(见图1)。

计算中只考虑无限深透水坝基渗流,认为土石坝为不透水体。坝前水深在5～30 m内变化;考虑到与后期的试验相一致,坝基土体通过实验室人为配置其颗粒级配,分别采用黏壤土、粉土、粉砂三类,各类土基本物理性质见表1。

表1 数值计算土体物理性质指标Tab.1 Basic physical property indexes of soil used in tests

悬墙深度呈n倍水头递增,计算无限深透水坝基渗流量和渗透坡降的变化规律。以坝前水头5 m为例,当坝基土体为粉砂时,分别计算出防渗墙深度为5,10,15,20,25,…,200 m时的单宽渗流量、防渗墙底部和下游坝脚处的渗透坡降。进而变换坝基土体的渗透系数,重复上述计算。即获得坝前水深5 m时悬墙控渗的相关数据。进而再计算坝前水深为10,15,25和30 m时的相关数据。

文中采用有限元软件Geo-Studio(SEEP/W)模块链接无限元单元,需要注意的问题如下:①无限元模拟的是远场区域近似的线性变化,因此无限元的材料只能是线弹性材料;②无限元的节点和实体单元一样,应按逆时针方向编号,并且要确保无限元的第一个面是与有限元交接的面,这一项是建好模型后在Geo-Studio的输入文件(inp文件)里手动修改的[8];③无限元的延伸方向必须是发散的,不能交叉[9]。

有限元与无限元结合对无限深透水坝基进行单元剖分。当坝前水深为5 m时,计算云图如图2。

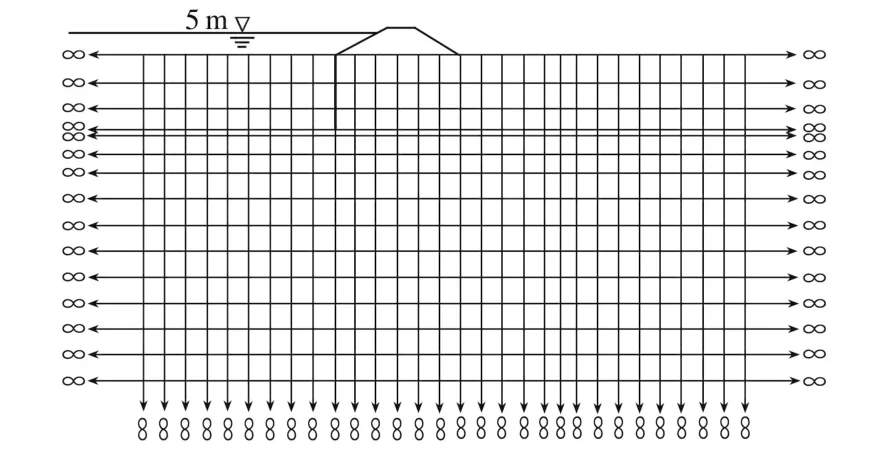
图1 有限元-无限元计算模型网格剖分Fig.1 Model unit subdivision IEM-FEM

图2 渗流数值计算等势线Fig.2 Seepage equipotential line given by numerical calculation

2 计算结果分析

2.1 渗流计算结果

通过上述数值模型计算坝后渗流量、渗透坡降随防渗墙深度的变化规律,如坝前水深5 m,坝基渗透系数为1×10-3cm/s时,不同防渗墙深度,渗流计算结果见表2。进而变换水头,计算出水头差△H=10～30 m时,渗流量q、渗透坡降J随防渗墙深度s增加时的数据,并绘制关系曲线;同理,计算并绘制出坝基不同土体时,渗流量q随悬墙深度s增加的变化曲线(见图3)。

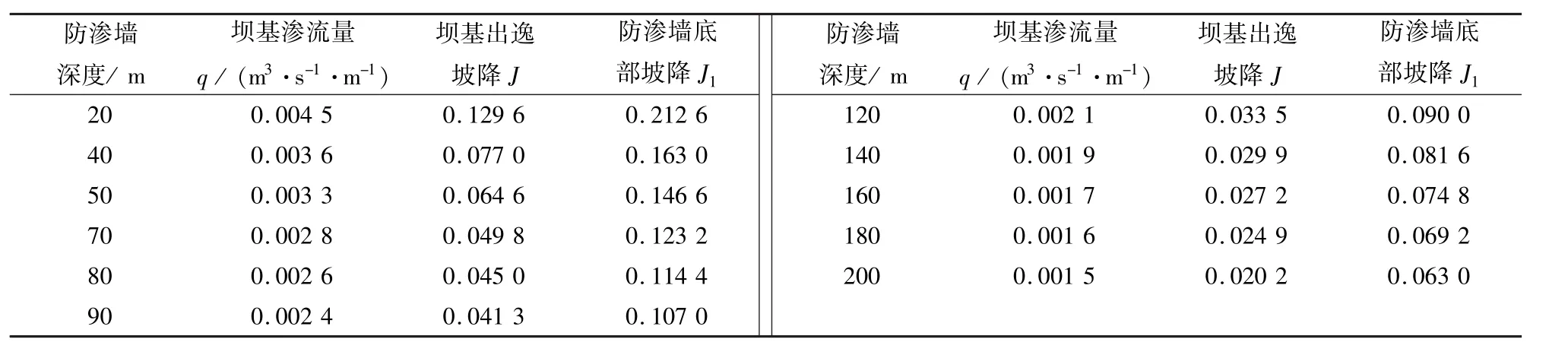
表2 坝基渗流量q和渗透坡降J随悬墙深度变化Tab.2 Variation of q and J with the depth of the cut-off wall

图3 各类土体时各水头下q随s变化曲线Fig.3 Curves of q-s of different kinds of dam foundation soil under different water heads

计算发现,对于均质坝基,渗流场各点坡降变化与坝基土体的渗透性无关,只与水头和防渗墙深度有关。因此各渗透系数下渗透坡降随防渗墙深度变化曲线是一致的(图4)。

2.2 坝基渗流量曲线拟合分析

针对图3,应用Origin8.0软件中多种函数进行拟合,结果发现渗流量变化曲线与对数函数曲线能高度拟合,汇总各渗透系数下计算结果拟合曲线函数见表3。

综合考虑坝基渗透系数k、上下游水头差ΔH和防渗墙深度s变量对公式的影响,得到统一计算式:

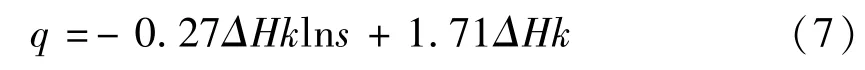
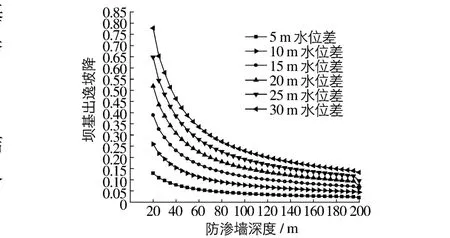
图4 各类土体时各水头下J随s变化曲线Fig.4 Curves of J-s of different kinds of dam foundation soil under different water heads

表3 不同渗透系数时q随s变化关系式Tab.3 Functions of q with s by different permeability coefficients of foundation

由式(7)可知,当坝基渗透系数k和防渗墙深度s一定时,渗流量ΔH与上下游水头差成正比;同理,当ΔH和s一定时,坝基渗透系数越大渗流量越大,且呈正比;当ΔH和k一定时,坝基渗流量则与lns呈一次线性关系,截距为1.71ΔHk。

由此可见,随着防渗墙深度的增加,坝基渗流量会越来越小,控渗效果也越来越好,但相应的工程造价和施工难度也会越大。以坝前水深10 m,坝基土体为粉砂土为例,若坝基渗流量趋于0,则防渗墙深度要达到558 m。这在目前的工程技术条件是无法实现的,也是不必要的。

2.3 出逸坡降分析

绘出不同渗透系数为渗流量和渗透坡降的关系曲线见图5,分析发现,在坝基渗透系数和水头一定情况下,随着防渗墙深度增加,二者的变化规律呈直线型。

由图5可知当坝基土体为粉砂时,坝后渗流量和渗透坡降的关系为:

当坝基渗透系数k发生变化后,式(8)可改写为:

由式(9)可反求出坝基渗透出逸坡降表达式为:

由式(10)可知,坝基渗透出逸坡降与悬墙深度呈非线性递减关系。可以通过延长防渗墙深度来减小坝基出逸坡降。

此外,通过计算还发现,防渗墙底部坡降随着悬墙深度的增加也呈递减趋势(见表2和图6),而非递增。这是因为对于无限深透水坝基来说,悬墙深度相对较小,渗透坡降递减趋势明显。但若坝基中存在弱透水层,防渗墙底部坡降会呈递增趋势。

图5 渗透坡降和渗流量关系曲线Fig.5 Relationship curves of seepage gradients and seepage discharge

图6 防渗墙深度与底部渗透坡降关系Fig.6 Relationship between seepage gradients at bottom of the cut-off wall and its depth

3 试验验证

3.1 试验设计与用土

为了验证上述计算式的正确性,在室内利用渗流槽来模拟无限深坝基悬墙防渗。根据文献[8]可知,渗流槽模型遵循Darcy定律比尺关系为:流速λv=λk;单宽流量λq=λλk;流量λQ=λ2λk。

本试验中渗流砂槽为立方体,长6.0 m,宽0.7 m,高2.7 m。砂槽模型的长度比尺取200,则

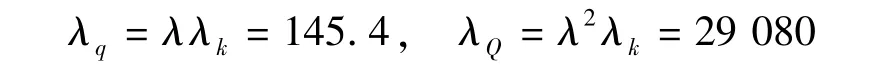
为了和数值计算时各模型渗透系数保持一致,试验用土选用表1中土体。

3.2 渗流槽结构设计

渗流槽长6 m,宽0.7 m,高2.7 m,槽一侧采用有机玻璃制成。整体结构由储水及溢流系统、槽身、测压管系统、出逸系统等部分组成(图7)。

储水及溢流系统用来维持坝前水头恒定,出逸系统用以收集坝后渗流水量,槽身的测压管,可以测量渗流槽内不同点水位。试验时由储水系统注水,并通过储水罐调整到要求高度。槽身填筑坝基土体,根据坝前水深不同,模型中土层厚度为2.5～2.8 m。渗流槽下游末端开有渗流观测孔,观测孔接量筒,用以观测渗流量变化。

坝基土体填筑完毕后,在坝基上修筑土石坝模型。土石坝模型采用黏土填筑,表面用土工膜包裹(图8),确保不透水。坝轴线距上游砂槽端部4 m,距下游端部2 m,上下游边坡均取1∶2;坝前水深可根据需要取5～30 cm。

长度比尺选为200,则由模型确定的原型尺寸为:坝前水深为5～30 m,坝基深度为410～440 m,属单层无限深透水地基,坝轴线距上游砂槽端部800 m,距下游端部400 m,上下游边坡均取1∶2。

图7 渗流模型Fig.7 A seepage model

图8 采用土工膜作为悬墙材料Fig.8 Geomembrane used as the suspended wall materials

3.3 试验步骤

(1)装样。按照干密度来控制试验用土,为了防止水沿渗流槽边壁侧渗,在槽内壁用红黏土涂抹,在有机玻璃一侧采用凡士林涂抹[10],再将定量的试验用土填入模型槽中,分层击实,并保持均匀。

(2)防渗墙模拟。用不透水的白色土工膜模拟防渗墙,同样通过涂抹凡士林和黏土来将土工膜防渗墙与槽身侧面进行无缝黏接,确保不侧渗。防渗墙位于上游坝角处。防渗墙深度根据试验要求分别是n倍水头差递增。

(3)渗流稳定。土体填入槽中后,通过储水和溢流系统在坝前供水,使水逐渐渗入到土体中使土体饱和。每次试验需要前期的稳定期,即土体的饱和时间,根据土体的不同饱和时间约为1～5 d,即在此时间段内的数据不能作为试验数据。

(4)渗流和渗透变形试验。储水系统和溢流系统将坝前水位保持恒定,待渗流稳定后观察测压管中的水位变化。同时用量筒收集下游出逸口水量,并记录单位时间内的水量。当下游单位时间内渗流水量保持不变时,确定各点的渗透压力和坝后渗流量。

(5)悬墙深度变化。某一深度的悬墙相关渗流数据测完后,需要改变悬墙的深度,则需要将坝前的土体挖开,延长悬墙深度,再进行土体回填,为了确保数据精度,回填土体也需要确保渗透稳定后才能开始采集数据。同一指标需采集3组数据,求平均值。坝前水位变换时,重复上述步骤,测出悬墙深度变化时,渗透坡降和渗流量的变换规律。

(6)换土。某一渗透系数的土体试验完毕后,需要更换砂槽内土体。重复试验步骤(1)～(5),收集不同渗透系数坝基渗流量和渗透坡降数据。

3.4 试验结果对比分析

由于试验渗流槽尺寸的限制,在室内只针对坝前水头5,10和15 m三种情况进行模拟试验。测得渗流量数据后通过λQ=λ2λk=29 080转换成实际流量。以粉砂土体为例,试验收集水头分别为5,10和15 m时坝基渗流量如表4所示。根据坝基渗流量试验值和理论计算数据绘制对比图(图9)。

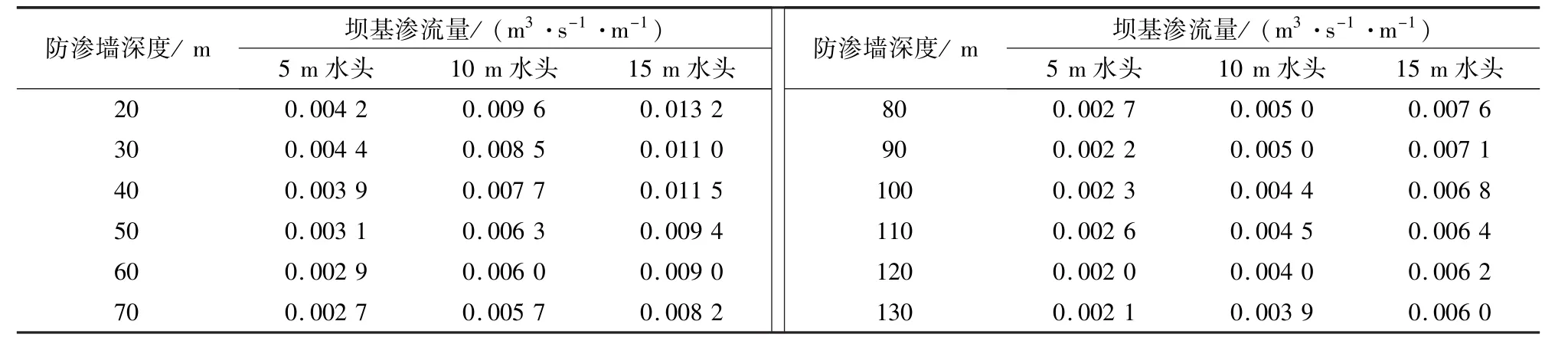
表4 粉砂土时不同水头坝基渗流量试验值Tab.4 Test values of silt sand under different water heads

图9 不同坝基土时渗流量试验值和理论值对比Fig.9 Comparison between the test and theoretically calculated values of different dam foundation soils

通过试验同样可见,坝基土体的渗透系数大小与坝基各点的坡降变化无关,只与上下游水头差和悬墙深度相关。绘制各土层情况下坝基渗透出逸坡降试验值与理论值对比见图10。

试验与理论值比较不难发现,试验数据虽有所变化,但总体变化趋势与理论值一致。从而验证了理论模型及计算结果的正确性。此外。通过分析发现试验数据变化的主要原因是模型中渗透系数差异、水位扰动、渗流槽侧渗和测压管堵塞等等人为和仪器误差造成的,此外与模型尺寸相对较小也有关系。

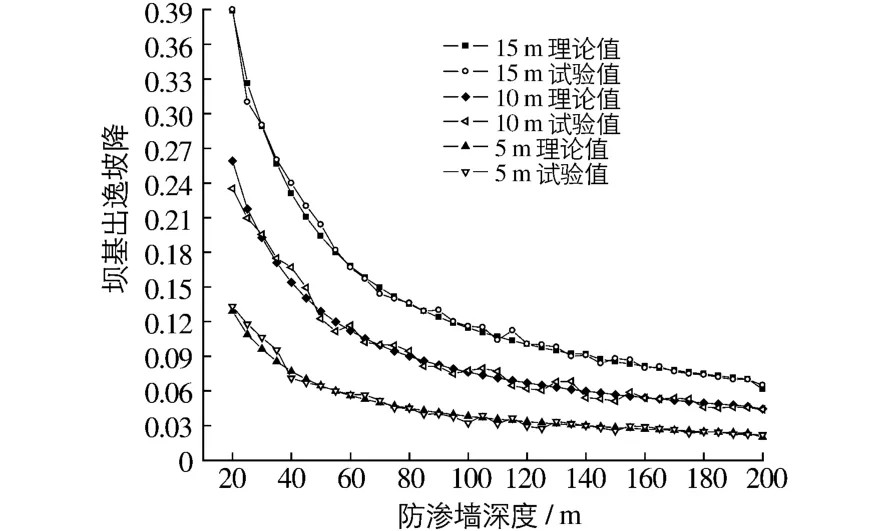
图10 各类土体坝基出逸坡降试验值与理论值比对Fig.10 Comparison between the test and theoretical values of exit gradient under different soils

4 结 语

通过建立有限元—无限元数值模拟,计算出无限深透水坝基上土石坝坝基渗流量、渗透坡降随悬墙深度的变化规律;在室内通过渗流槽模拟了无限深透水坝基不同渗透系数时,渗流量和渗透坡降随悬墙的变化规律,验证了理论计算的正确性。在此基础上本文得出以下几点结论:

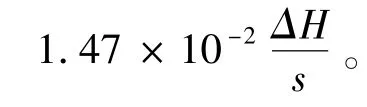
(2)当坝基为均质渗透介质时,坝基渗透坡降变化与坝基土体渗透系数无关,只与悬墙深度和上下游水头差相关。

(3)当坝体为低坝时,根据实验室常用级配良好土体的物理参数和文中计算结果不难发现,悬墙深度约为3～6倍坝前水头,渗透稳定基本可满足要求。

综上所述,无限深透水地基中采用悬墙控渗的情况下,理论上渗流量和渗透坡降都可以达到预期目标。但对于渗流量的控制需要防渗墙深度很大,有的在技术上无法实现。因此,实际上需要结合坝基内部的弱透水层或水平铺盖联合防渗,效果会更明显。本文数值计算和试验模型只针对均质单层透水介质,较理想化,具有局限性,但能为揭示悬墙控渗规律提供理论参考。

[1]唐益群,施伟华,张先林.关于流土和管涌的试验研究和理论分析[J].上海地质,2003(1):25-31.(TANG Yi-qun, SHI Wei-hua,ZHANG Xian-lin.The experiments study and theoretical analyses of piping and flow soil[J].Shanghai Geology, 2003(1):25-31.(in Chinese))

[2]杨桂芳,姚长宏.长江干堤管涌研究现状及其发展趋势[J].江西地质,2001,15(1):50-52.(YANG Gui-fang,YAO Chang-hong.Current situation and development trend in the study of piping in the main dam of the Yangzi River[J].Jiangxi Geology,2001,15(1):50-52.(in Chinese))

[3]高江林,陈云翔.基于渗流与应力耦合的防渗墙与坝体相互作用的数值模拟[J].水利水运工程学报,2013(2):58-63. (GAO Jiang-lin,CHEN Yun-xiang.Cut-off wall and dam body seepage and stress coupling based on the numerical simulation of the interaction[J].Hydro-Science and Engineering,2013(2):58-63.(in Chinese))

[4]刘忠玉,乐金朝,苗天德.无黏性土中管涌的毛管模型及其应用[J].岩石力学与工程学报,2004,23(22):3871-3876. (LIU Zhong-yu,YUE Jin-chao,MIAO Tian-de.Capillary-tube model for piping in no cohesive soils and its application[J]. Chinese Journal of Rock Mechanics and Engineering,2004,23(22):3871-3876.(in Chinese))

[5]李守德,徐红娟,田军.均质土坝管涌发展过程的渗流场空间性状研究[J].岩土力学,2005,26(12):2001-2004.(LI Shou-de,XU Hong-juan,TIAN Jun.Researches on three-dimensional seepage fields of soil dam under piping erosion[J].Rock and Soil Mechanics,2005,26(12):2001-2004.(in Chinese))

[6]毛海涛,侍克斌,李玉建.无限深透水地基上土石坝坝基垂直防渗的保角变换渗流计算[J].水利水运工程学报,2008 (4):71-77.(Mao Hai-tao,Shi Ke-Bin,Li Yu-jian.The infinite deep pervious foundation earth rock dam seepage cutoff conformal transformation[J].Hydro-Science and Engineering,2008(4):71-77.(in Chinese))

[7]肖四喜,李银平.大堤管涌形成机制分析及治理方法[J].湖南大学学报:自然科学版,1999,26(2):123-126.(XIAO Si-xi,LI Yin-ping.Mechanism analysis and remedy of water gushing through pipes in main dam[J].Journal of Hunan University (Natural Science),1999,26(2):123-126.(in Chinese))

[8]李士峰.佳木斯市松花江堤防防渗工程设计[J].水利水运工程学报,2003(1):75-78.(LI Shi-feng.Songhua River levee project design of Jiamusi City[J].Hydro-Science and Engineering,2003(1):75-78.(in Chinese))

[9]张家发,吴昌瑜,朱国胜.堤基渗透变形扩展过程及悬挂式防渗墙控制作用的试验模拟[J].水利学报,2002(9):108-111,116.(ZHANG Jia-fa,WU Chang-yu,ZHU Guo-sheng.Experimental study on seepage deformation propagation control using impervious wall of suspension type[J].Journal of Hydraulic Engineering,2002(9):108-111,116.(in Chinese))

[10]周健,张刚,孔戈.渗流的颗粒流细观模拟[J].水利学报,2006(1):28-32.(ZHOU Jian,ZHANG Gang,KONG Ge. The seepage of mesoscopic simulation of particle flow[J].Journal of Hydraulic Engineering,2006(1):28-32.(in Chinese))

[11]ERUIN M C,BENSON N D,MORGAN J R,et al.Melbourne′s south bank interchange:a permanent excavation in compressible clay[J].Canadian Geotechnical Journal,2004,41(5):861-876.

[12]TEDD P,JEFFERIS S A.The use of slurry trench cut-off walls to repair embankment dams in the UK[C]∥Proceedings of the British Dams Society Conference.[S.l.]:[s.n.],2000:425-438.

Experimental studies on seepage control of suspended cut-off wall on infinite deep pervious foundation

MAO Hai-tao1,2,3,HE Hua-xiang3,SHAO Dong-guo1,WANG Xiao-ju1
(1.College of Civil Engineering,Chongqing Three Gorges University,Chongqing 404100,China;2.School of Water Resources and Hydropower Engineering,Wuhan University,Wuhan 430072,China;3.Chongqing Three Gorges Water Conservancy and Electric Power Co.,Ltd.,Chongqing 404100,China)

Seepage control of foundation with the deep overburden layer which can be considered as the infinite deep pervious foundation is one of the key problems that determines the success or failure of dams construction.The suspended cut-off wall has been used as the anti-seepage structure in the same projects,but analysis of its seepage control effects and percolation mechanism has no common understanding in the theory.In order to make deep studies of the seepage control effects and percolation mechanism of the suspended cut-off wall,a model in combination with the infinite element method is established to simulate the infinite deep pervious foundation, analyzing the variation in seepage discharge and seepage gradients under the conditions of different permeability coefficients k,depth of the cut-off wall s and the water head difference ΔH,and fitting out the calculation formulas having high accuracy.The verification tests have been done in those studies.And the experimental study results show that the calculation formulas are right.From those studies it is found that the seepage control impacts of the cut-off wall are more significant than the infinite deep pervious foundation in controlling the seepage gradients,and the cut-off wall can effectively control seepage-induced damages;and in controlling seepage discharge,the greater the depth of the cut-off wall is,the more significant the effect is,but it needs auxiliary measures to realize reasonable goals in economy and technology.The analysis results of the studies are helpful to further understanding of the seepage control principles of the suspended cut-off wall.

infinite deep pervious foundation;seepage;earth-rock dam;suspended cut-off wall;infinite element and finite element;seepage gradients

TU223.4

A

1009-640X(2014)04-0044-08

2014-03-10

国家自然科学基金资助项目(51309262);重庆市教委科学技术研究项目(KJ121104);重庆三峡学院重点项目(12ZD20)

毛海涛(1980-),男,山西运城人,副教授,博士,主要从事土石坝渗流机理研究。E-mail:maohaitao1234@163.com