强夯地基垫层厚度对承载力与变形模量的影响

岳喜兵,江舜武,王宝善,邓永锋

(1.东南大学 岩土工程研究所,江苏 南京 210096;2.江苏省交通规划设计院股份有限公司,江苏 南京210014;3.连云港新海湾码头有限公司,江苏 连云港 222000;4.连云港港口集团有限公司 工程管理部,江苏 连云港 222000)

强夯地基垫层厚度对承载力与变形模量的影响

岳喜兵1,2,江舜武3,王宝善4,邓永锋1

(1.东南大学 岩土工程研究所,江苏 南京 210096;2.江苏省交通规划设计院股份有限公司,江苏 南京210014;3.连云港新海湾码头有限公司,江苏 连云港 222000;4.连云港港口集团有限公司 工程管理部,江苏 连云港 222000)

对江苏省连云港赣榆港区吹填土强夯地基进行了两组现场载荷试验,探讨不同强夯垫层厚度的强夯地基承载力特性。在现场试验基础上,采用有限元法分析垫层厚度对附加应力系数和传递深度的影响,结果表明强夯垫层能有效增大附加应力的扩散作用,明显提高地基承载力,附加应力在2倍板径深度范围内下降到板底应力的6%以下;但地基土屈服后会使附加应力往深层传递。综合数值模拟的结果分析,表明附加应力与自重应力比值为0.2时所确定的计算深度随板底应力水平的增大而增大,不是一个固定值。在此基础上探讨了载荷试验反演的地基变形模量与按垫层厚度的加权模量间的关系,结果表明按厚度加权获得的地基平均模量为载荷试验反演的变形模量的1.2倍。

载荷试验;垫层厚度;影响深度;变形模量;附加应力系数

载荷试验作为一种现场承载力测试方法,在地基勘察与检测中得到广泛应用。王成锋[1]、陈国政[2]认为大直径载荷试验可以克服因承压板尺寸造成的土体均匀性差异,能够全面反映地基的强度和变形特征,提出载荷板的影响深度约为2.0D～2.5D(D为载荷板直径或宽度)。李飞等[3]对多种不同垫层厚度的载荷试验研究,发现它们的p-s曲线存在明显差异,垫层厚的曲线舒缓,总沉降量小。地基处理中为了施工便利而人工设置一定厚度刚度较高的碎石或砂垫层,由于面积较大,可以将其看成“人工硬壳层”,由于具有壳体效应、封闭效应、反压护道作用等特点[4],常被用于软土地基中,从而形成上硬下软的双层地基。硬壳层的板体效应早在19世纪40年代已被国外学者所认识,A.E.Cummings[5]研究了圆形荷载作用下刚性底板双层地基中的应力问题,解出荷载中心线下不同深度处的垂直应力。D.M.Burmister[6]提出了一种用于计算含2层或3层成层土的应力和位移的计算解,并给出圆形面积上受均布荷载时地基土的应力和位移。

在国内,唐建中[7]等通过双层地基矩形均布载荷模拟试验,探讨了双层地基应力扩散特性;王晓谋等[8]指出竖向应力扩散作用随着垫层厚度的增加而扩大;杨果林[9]通过室内模型试验,得出了含软弱下卧层双层地基的界面附加应力分布规律。徐洋等[10]以弹性地基梁理论为依据解释双层地基的应力扩散效应,并在此基础上提出了应力扩散系数的计算公式。吴邦颖等[11]进行了公路软基人工硬壳层的研究,得出硬壳层起到了扩散应力、减少软土地基沉降和侧向位移的作用。但需强调的是,至今对于硬壳层的厚度和刚度对应力扩散的影响鲜有系统的研究。为此,本文在现场试验的基础上采用Geo-slope有限元数值模拟软件,对设置不同厚度和模量的人工垫层地基进行附加应力系数的计算分析,探讨载荷试验的影响深度与垫层厚度的规律,建立载荷试验反演地基综合变形模量与按地层厚度的加权模量间的关系。

1 场地及强夯工艺

本场地位于连云港赣榆港区,该港区入海大约10 km,由吹填深海中泥砂组成,由于吹填方式、吹填原土层、吹泥口位置和水力分选等因素导致吹填场地土层均匀性较差。场地中的砂层以松散状态的中粗砂为主,黏土层以软塑为主,黏土层中含砂量较大,局部含碎石及钙质结核。该场地地质条件如下:0～2 m段以黏性土为主,可塑,黄褐色,灰白色;2～4 m段黏性土混杂大量中粗砂砾,砂含量约40%～50%;4～6 m段中粗砂混黏性土,黏性土可塑～硬塑;6～8 m段以黏性土混中细砂为主,灰白色,黄褐色,可塑～硬塑;8～10.8 m段以中细砂混黏性土为主,局部含有淤泥质土。

本次强夯试验机械采用履带式夯机,夯锤底部为圆形,直径2.2 m,夯锤质量16 t,最大落距17 m。试验区场地夯前满铺约1.3 m厚碎石,碎石级配要求良好。首先进行间隔点夯,夯击能为2 000 kN·m,然后进料整平至初始标高,再进行夯击能为800 kN·m的满夯试验,最后整平场地至设计标高进行载荷试验。

2 现场载荷试验

图1 载荷试验p-s曲线Fig.1 p-s curves of plane loading test

选取试验段中心较平坦区域作为试验场地,先后进行0.2和1.3 m两组不同垫层厚度载荷试验,圆形载荷板面积为5.09 m2(板径为2.55 m),载荷试验的整个过程根据《建筑地基基础设计规范》(GB 50007-2011)附录C的有关要求进行。第1组(1#～3#试验点)在群夯后的碎石地面(碎石垫层厚度约为1.3 m)上进行,第2组(4#～6#试验点)在挖除碎石(碎石垫层厚度约为0.2 m)场地上进行。两组载荷试验的p-s曲线如图1,承载力和变形模量列于表1。其中承载力按《岩土工程勘察规范》(GB50021-2001)确定,变形模量为:

式中:E0为地基的变形模量(MPa);μ为泊松比,计算中按0.30取值,即表层碎石垫层与下层的黏土-砂混合层泊松比的均值;D为板直径(m),取2.55 m;p为比例界限荷载(kPa);s为比例界限对应的沉降(mm)。

表1 载荷试验结果Tab.1 Results of plane loading tests

图1表明,6个试验点载荷试验的沉降量在极限荷载下(设计承载力为165 kPa)均没有达到破坏标准(6%,15.3 cm),进而根据规范按极限荷载的一半和0.01D变形对应荷载的最小值确定。为此,第1组(1#～3#)载荷试验中承载力按极限荷载的一半进行确定,根据第1组(1#～3#)载荷试验的结果,地基承载力标准值为165 kPa。第2组(4#～6#)载荷试验的垫层厚度相对第1组较薄,载荷板的沉降量相对较大(均大于60 mm,但仍未达到0.06D的破坏变形),按变形确定的承载力标准值为160 kPa。单从承载力确定的结果上来看,垫层厚度效应不明显,主要原因在于设计承载较低,导致载荷试验时最大配载相对较小,在极限荷载作用下地基未能达到破坏。尽管如此,对比两者总沉降量可发现,碎石垫层的厚度对地基沉降的控制起到了一定的作用,较大刚度的垫层可以大大减小地基的总变形。进一步分析地基的变形模量,发现第1组载荷试验点的变形模量为12.2～38.0 MPa,平均为25.0 MPa;第2组载荷点的变形模量为7.8～9.0 MPa,平均为8.4 MPa,再次表明了碎石垫层厚度对地基刚度有较大的影响。

为进一步了解垫层刚度对地基变形和强度的影响,后续将以该载荷试验为原型,建立载荷试验有限元模型,进行数值模拟分析。

3 数值模拟与理论分析

在本文有限元数值计算中,垫层采用线弹性模型,根据现场载荷试验得知土体基本处于弹性变形阶段,在加载后期呈现塑性变形特征,地基土采用摩尔-库伦理想弹塑性模型,计算模型和参数如图2和表2所示。计算选用轴对称模型,模型大小为40 m×12.5 m,载荷板半径为1.25 m。边界条件为:土层底部采取固定水平向和竖向位移,竖向边界固定水平向位移。为了准确模拟载荷板附近应力和变形,将图2中的局部区域进行网格加密。计算中荷载施加方式同现场载荷试验相同。为了分析不同垫层厚度对地基承载力和压缩、变形模量的影响,计算中垫层厚度分别取为0,0.5,1.0,1.5,2.0和2.5 m。为了能够更加准确地模拟同一工况条件下土层的变形规律及变形模量,当垫层厚度逐渐增加时,保持计算土层厚度不变,即均取10 m。

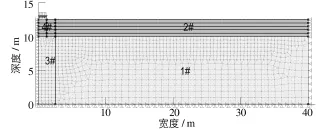
图2 数值模拟模型Fig.2 A numerical simulation model

表2 数值模拟参数取值Tab.2 Parameters in the numerical simulation

3.1 垫层效应分析

根据不同厚度垫层数值模拟所得的p-s曲线(图3),可见垫层越厚,总沉降量越小,在无垫层的情况下,土体的总沉降为122.9 mm,在逐渐增加垫层厚度时,沉降量呈现逐渐减小的趋势,并最终保持稳定。在垫层厚度取1 m时,载荷板的总沉降减小到46.7 mm,减小幅度约为62%。当垫层厚度增加到2.5 m时,载荷板总沉降量降至26.0 mm,总沉降量较不加垫层时降到原来的1/5。以上结果说明较大刚度的垫层能够有效地控制强夯地基总沉降量,垫层厚度越厚地基总沉降量越小。图3也表明板底应力在108 kPa时地基土基本呈弹性状态,在216 kPa时0.5 m垫层下的地基土进入塑性状态,而在324 kPa时垫层厚度大于1.0 m的地基土基本上仍处于弹性状态。不同垫层厚度的载荷板中心深度的附加应力系数的分析结果见图4,板底应力分别为108, 216和324 kPa,Z为试验点的深度。

图4表明,不同应力水平状态下,载荷板中心1倍板径深度范围附加应力系数k迅速降低到0.25左右,且随着垫层厚度的增加,附加应力系数k逐渐减小;在2倍板径深度范围内,附加应力系数k逐渐降低,降低幅度逐渐减小,并趋于稳定,稳定值约为0.06。深度继续增加,附加应力系数k变化微弱并趋于稳定。

结合图3的分析,图4(a)中地基土基本都处于弹性状态,此时附加应力系数的结果表明了垫层的应力扩散作用;同样图4(b)和(c)中弹性地基中垫层仍表现出应力扩散的作用,即垫层越厚扩散效应越明显。需要强调的是,对比图4中3种情况,发现没有垫层的地基附加应力是增大的,其原因为随着附加应力逐渐增加,表层土逐渐屈服,进而使附加应力往下传。

图3 不同垫层厚度的p-s曲线Fig.3 p-s curves with cushions having different thicknesses

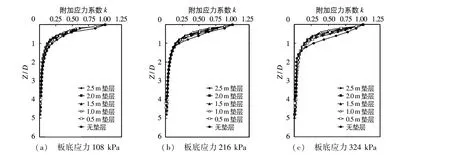
图4 不同应力水平下附加应力系数k随Z/D变化曲线Fig.4 Additional coefficient k at different stress levels

3.2 载荷试验影响深度

文献资料[12]表明,地基附加应力的影响范围为附加应力等于自重应力的20%,即σz=0.2σc。本文进一步探讨考虑地下水位以及应力水平对载荷试验深度的影响。分析计算中,地下水位按0和1.0 m计。各应力水平下,附加应力的分布与自重应力的分布如图5。

图5 附加应力随Z/D变化曲线Fig.5 Additional stress distribution

由图5可见,当应力水平为108,216和324 kPa时,载荷试验的影响深度(附加应力等于自重应力的20%的深度计)分别为1.2D～1.4D,1.8D～2.0D和2.0D～2.4D,即载荷试验的影响深度随着应力水平的增加而线性增加。换言之,已有研究成果[13-14]所提出的载荷板的影响深度约为2.0D～2.5D这一结论需要进一步商榷,即在评估载荷试验影响深度时应考虑应力水平。

3.3 地基平均模量算法

虽然通过载荷试验结合表达式(1)可以计算出地基的平均变形模量,但在工程具体实践中一般采用厚度的加权平均法进行计算。为此有必要评价目前常用的厚度加权平均法获得的地基平均变形模量与载荷试验获得的模量间的相关性。

根据对不同垫层厚度时数值模拟的地基承载力和变形模量统计分析,变形模量通过表达式(1)进行反演,计算结果如表3中“反演变形模量”所示。在公路工程中,地基的变形模量一般采用厚度加权(即“串联”和“并联”加权两种模式)进行计算,计算公式如下:

根据表2的参数和式(2)和(3)可以分别计算串联和并联的地基变形模量(表3)。需要强调的是,根据3.3节的分析,计算中取载荷板的影响深度为5 m,即H为5.0 m。

表3 不同厚度垫层对应的承载力与变形模量Tab.3 Bearing capacity and deformation modulus in contrast to cushions with different thicknesses

表3表明地基在不做任何垫层处理时,其承载力为144 kPa,在逐渐增加垫层厚度的过程中,承载力呈现逐渐增加的趋势,当垫层厚度超过0.5 m时,承载力即可达到160 kPa。变形模量也随着垫层厚度的增加而逐渐增加,即变形模量从不加垫层的8.1 MPa增加到20.6 MPa。图6为反演/计算得到平均变形模量和垫层厚度关系,表明了3种方法得到地基平均变形模量与垫层厚度间基本上呈线性增长的关系,但是式(1)和(2)确定的地基平均变形模量对垫层厚度变化敏感。

进一步分析图6和表3,通过载荷试验反演的地基平均变形模量与式(2)计算的变形模量值较为接近,相对误差仅在10%～30%以内,并逐渐趋于一个稳定值;而式(3)计算的变形模量的相对误差随着垫层的增加呈逐渐增加的趋势。同时,式(2)获得的地基平均模量较式(1)大,而式(3)则正好相反,其原因在于式(2)基于“串联”模式,其数值趋向于大值;而表达式(3)基于“并联”模式,其数值趋向于小值。

为了进一步分析明确根据载荷试验反演的地基平均模量与厚度加权模量间的关系,以反演的模量为横坐标,2种加权模量为纵坐标进行拟合(图7)。

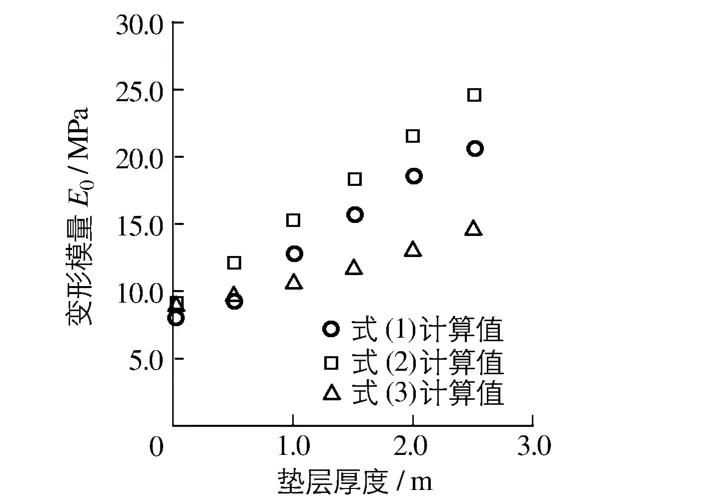
图6 变形模量与垫层厚度的拟合曲线Fig.6 Relationships between deformation modulus and cushion thickness

图7 反演模量与加权模量的拟合曲线Fig.7 Fitting curves of back modulus and weighted modulus

图7表明式(2)与式(1)获得的地基模量统计关系较好,离散性较小,二者为1.2倍的关系,即E02= 1.2E01;式(3)与式(1)间的模量关系为E03=0.8E01。通过建立的经验关系式,可为工程中存在硬壳层的双层地基的平均变形模量的预估提供参考。根据该经验关系(E02=1.2E01)计算得到现场垫层厚度为0.2和1.3 m的复合地基的变形模量为8.8和14.7 MPa,与现场载荷试验计算的变形模量较为吻合,验证了分析的合理性。

4 结 语

本文对连云港赣榆港区强夯地基现场载荷试验结果进行了分析,并结合了Geo-slope有限元数值模拟研究了垫层厚度对地基承载力及平均变形模量的影响,得到以下结论:

(1)通过数值模拟分析,得到附加应力系数随着深度的增加逐渐减小并趋于稳定,随着垫层厚度的增加而减小,垫层的设置有助于附加应力的扩散,明显提高了地基的承载力。但是当地基土屈服后,会加大往深层传递的附加应力。

(2)在2D深度范围内,附加应力系数减小到板底应力6%以下;附加应力与自重应力的比值为0.2时确定的影响深度随板底应力水平的增大而增大,不是一个固定值。

(3)根据载荷试验反演地基变形模量E01与按厚度加权模量存在线性关系,为E02=1.2E01,可为工程中存在硬壳层的双层地基平均变形模量的预估提供参考。

[1]王成锋,刘宏,高振鲲,等.载荷板尺寸效应对水泥土搅拌桩静载试验的影响[J].建筑科学,2007,23(11):53-55. (WANG Cheng-feng,LIU Hong,GAO Zheng-kun,et al.Influence of size effect of loading plate on static load test results of soilcement mixed piles[J].Building Science,2007,23(11):53-55.(in Chinese))

[2]陈国政.复合地基检测中现场小型载荷试验与大型载荷试验对比研究[J].工程勘察,1988(1):21-25.(CHEN Guozheng.Comparison between small-scale and large-scale loading tests in composite foundation test[J].Geotechnical Investigation and Surveying,1988(1):21-25.(in Chinese))

[3]李飞,刘松玉.水泥土桩复合地基承载力确定的几个问题[J].东南大学学报,1999,29(增1):94-98.(LI Fei,LIU Song-yu.On the bearing capacity of soil-cement mixing pile composite foundation[J].Southeast University Press,1999,29 (Suppl1):94-98.(in Chinese))

[4]付传飞.硬壳层软土地基工程特性研究[D].长沙:长沙理工大学,2009.(FU Chuan-fei.The engineering properties of hard shell layer soft soil foundation[D].Changsha:Changsha University of Science and Technology,2009.(in Chinese))

[5]CUMMINGS A E.Foundation stress in an elastic solid with a rigid underlying boundary[J].Civil Engineer,1941,11(11): 666-667.

[6]BURMISTER D M.The general theory of stresses and displacements in layered soil systems[J].Journal of Applied Physics, 1945,16(2):89-94.

[7]唐建中.双层地基应力扩散的特性研究[J].地基处理,1993,4(2):25-31.(TANG Jian-zhong.Research on properties of stress dispersion of double-layer foundation[J].Foundation Treatment,1993,4(2):25-31.(in Chinese))

[8]王晓谋,袁怀宇.河滩相软土地基路堤施工[J].长安大学学报:自然科学版,2003,23(3):26-29.(WANG Xiao-mou, YUAN Huai-yu.Embankment construction on alluvial soil foundation[J].Journal of Chang′an University(Natural Science Edition),2003,23(3):26-29.(in Chinese))

[9]杨果林.含软弱下卧层的双层地基工程特性试验研究[J].工程勘察,1998(1):1-5.(YANG Guo-lin.Research on engineering properties of double layer ground containing weak underlying stratum[J].Geotechnical Investigation and Surveying, 1998(1):1-5.(in Chinese))

[10]徐洋,谢康和.复合地基的平面应力扩散效应[J].土木工程学报,2002,35(2):57-60.(XU Yang,XIE Kang-he.A study of effect of plane stress dispersion in composite ground[J].China Civil Engineering Journal,2002,35(2):57-60.(in Chinese))

[11]吴邦颖,曹正康.公路软土路基人造硬壳层处理及研究[J].路基工程,1996(4):39-46.(WU Bang-ying,CAO Zhengkang.Treatment and research on artificial crust of soft soil foundation of highway[J].Subgrade Engineering,1996(4):39-46. (in Chinese))

[12]东南大学,浙江大学,湖南大学,等.土力学[M].北京:中国建筑工业出版社,2005.(Southest University,Zhejiang University,Hunan University,et al.Soil mechanics[M].Beijing:China Architecture&Building Press,2005.(in Chinese))

Analysis of impact of dynamic compaction foundation cushion thickness on bearing capacity and deformation modulus

YUE Xi-bing1,2,JIANG Shun-wu3,WANG Bao-shan4,DENG Yong-feng1
(1.Institute of Geotechnical Engineering,Transportation College,Southeast University,Nanjing 210096,China; 2.Jiangsu Province Communications Planning and Design Institute Limited Company,Nanjing 210014,China; 3.Xinhaiwan Port Co.,Ltd.,Lianyungang 222000,China;4.Project Management Department of Lianyungang Port Group Co.,Ltd.,Lianyungang 222000,China)

In this study,two groups of field loading tests are performed to study the influences of the cushion on the bearing capacity after the dynamic consolidation at Ganyu port in Lianyungang city.According to experimental data from two groups tests,the cushion thickness effects on the additional stress coefficient,influence depth of loading plate and average deformation modulus have been analyzed by using FEM numerical simulation.The analysis results show that the thickness of the cushion significantly reduces settlement and improves additional stress diffusion.And the additional stress coefficients would drop to below 6%of the stress at bottom of the plate at the 2 times of the plate diameter;when the foundation comes into yielding,the coefficients would be intensified.The influence depth of the plane load test would increase with the increase of the stress level at the plate bottom,not a constant ratio to the diameter of the plate.In addition,the relationships between the average deformation modulus weighted by the cushion thickness and that back-analyzed by the PLT tests are also discussed in this paper,and the results indicate that the the average deformation modulus weighted by the cushion thickness is 1.2 times higher than that of the latter,which can be used to estimate the reasonable foundation modulus.

plane loading test;cushion thickness;influence depth;deformation modulus;additional stress coefficients

TU472

A

1009-640X(2014)06-0084-07

2014-05-10

岳喜兵(1987-),男,安徽蚌埠人,硕士,主要从事公路路基路面设计工作。E-mail:yuexibing@seu.edu.cn 通信作者:邓永锋(E-mail:noden@sed.edu.cn)