基于黄金分割法的三视图识别
赵德胜,张 雪,李丽萍,郑 鹏,卜 康
(西安邮电大学 理学院,陕西 西安710121)
二维视图图纸原是工程技术人员进行技术交流的重要方式,但随着科学技术的发展,非专业技术人员与专业技术人员进行技术交流越来越普遍,而且,随着计算机技术和数控机床技术的发展,机械加工人员可以直接利用三维工程图进行机械零件加工,因此,二维图纸的发展受到一定的制约。与二维视图图纸不同,三维模型具有直观性强、交流便捷、以及可进行产品装配干涉检查等优点,因此,三维设计越来越受到人们的重视[1-3],所以,把二维工程图转化为三维图就很有必要。
把二维工程图转化为三维效果图算法的快速性、可靠性对于后续的三维重建具有决定性作用[4],而把二维工程图划分为主视图、俯视图、左视图以及辅助视图等各个视图区是其关键性的一步。
在视图划分时,由于三视图各个视图之间存在不连续特征,即在主视图与左视图、主视图与俯视图之间的空档中不存在任何图元,因此,可以利用这种特征找出主视图与左视图、主视图与俯视图之间的间隔区域,并在间隔区域各自画出一条直线作为二者分界线,从而把三个视图区别开[5-9]。
由于在实际工作中,工程图复杂程度不一。大部分工程图只有三个视图区(主视图、俯视图、左视图)组成,称为标准三视图。也有部分工程图有两个或多于三个视图组成。文[2,7]在视图识别时只考虑了标准三视图的情况,对于含有两个或多于三个视图的工程图则没有讨论。本文拟基于黄金分割优化算法给出一种视图识别方法,该算法不仅适用于标准三视图,而且适用于非标准三视图的情况。
1 优化模型建模原理
1.1 黄金分割法
黄金分割法是一种常用的一维搜索试探方法,又称0.618法。黄金分割法适用于搜索区间[a,b]上的任何单谷函数求极大(小)值问题,对函数没有连续性要求。其基本原理是:在搜索区间[a,b]内适当插入两点α1和α2,并计算其函数值。α1和α2将搜索区间分成三段。利用区间消去法原理,删去其中一段,使得搜索区间缩短。然后,在保留下来的区间上做同样的处理,如此迭代下去使区间无限缩小,从而得到目标值fmax(x)(或fmin(x))。黄金分割法要求插入点α1和α2相对于区间[a,b]的两端点具有对称性[10],即

其中λ为待定常数,通常取λ=0.618。
1.2 建模原理
黄金分割法通常用于对单谷连续函数f(x)求极大(或极小)值。其目标函数fmax(x)(或fmin(x))为未知量,通过不断缩小所搜区间[a,b],来求取一个x,使得

视图分界线的求取采用逐步试探的方式,即先作出一条直线,若不合格,则重作一条原直线的平行线进行再次判断,因此不同直线上的元素特征是不连续的。由于黄金分割法具有适用于离散函数的优点,故可用于视图识别。
由于视图分界线与工程图中的图元没有交点,而非视图分界线与图元存在交点,因此,把直线与图元交点的数量作为目标函数。由于视图分界线与图元无交点,取目标函数

把目标函数的直线作为视图分界线。
由于在工程图中,视图区分别按照横轴和纵轴方向分布,因此在视图识别时应分别按照横轴和纵轴方向进行识别。
在确定初始搜索区间时,也需要分别确定横轴和纵轴方向上的搜索区间。在纵轴方向上初始搜索区间应以纵轴方向上分布图元坐标的最大值和最小值作为初始搜索区间。在横轴方向与此相同。
2 纵轴方向上视图的识别
2.1 确定搜索区间及插入点
首先读取工程图中所有粗实线图元端点或顶点的坐标值。然后求出纵轴坐标值最大的点M1和最小的点M2。把M1的纵坐标值b作为区间上限,把M2的纵坐标值a作为区间下限,由此可得搜索区间[a,b]。
取λ=0.618,将M1和M2的纵坐标值b和a带入式(1)即可求得插入点α1和α2。
2.2 搜索并确定分界线
以(0,α1)为起点,作一条平行于横轴的直线l1。以(0,α2)为起点,作一条平行于横轴的直线l2。
判断l1、l2与图形中图元是否有交点,如果都无交点,则把直线l1和l2作为视图分界线。
若只有一条直线(假设为l1)没有交点,则把该直线l1作为视图分界线之一。取[α1,b]为新的搜索区间,开始新的搜索过程。如果在限定循环次数内仍不能确定分界线,则程序搜索终止。此时,程序认定不再有新的视图区。
如果l1、l2与图形中图元都有交点,则分别取l1和l2上所有交点中横坐标值最大点A1和A2,其横坐标值分别记为x1和x2,纵坐标值分别为y1和y2。再按以下步骤确定视图分界线。
设定ε的值,取点M2的横坐标值xM。如果
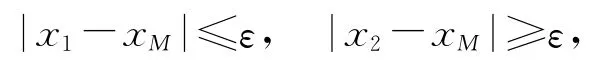
则取[y1,y2]和[y2,b]为新的搜索区间。如果

则取[a,y1]和[y1,b]为两个新的搜索区间。如果
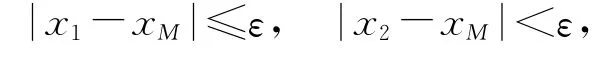
则取[y1,y2]为新的搜索区间。
确定新的搜索区间后,循环执行前述步骤即可得到视图分界线。如果经过有限次循环,仍不能确定视图分界线,且对于搜索区间[ymin,ymax]有
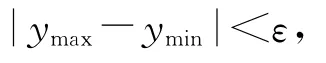
则程序自动终止。
3 横轴方向上视图的识别
利用已经读取的图形文件中所有图元端点或顶点的坐标值,求出横坐标值最大的点M1和最小的点M2。把M1的横坐标值by作为区间上限,把M2的横坐标值ay作为区间下限,由此可得搜索区间[ay,by]。
与纵轴方向上视图的识别过程相类似,可把主视图和左视图识别出来,并可判断是否存在右视图和后视图。
4 算例验证
例1(标准三视图的识别) 如图1所示三视图,L1为主视图和俯视图的分界线,L2为主视图与左视图的分界线。程序只需循环6次即可得到正确结果。
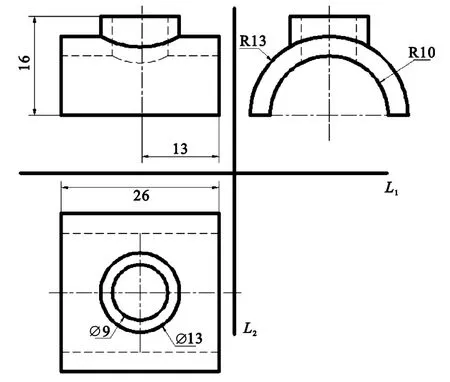
图1 标准三视图
例2(只含两个视图的工程图) 如图2所示的工程图只有两个基本视图,细实线为分界线。虽然主视图长度和左视图长度差别较大,循环次数较多,但程序只需循环10次即可得到正确结果。
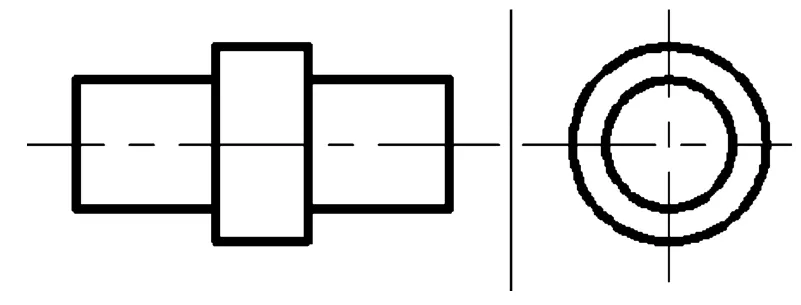
图2 少视图工程图
例3(具有多个基本视图的工程图) 如图3所示,图中细实线为各基本视图分界线。图中含有多个基本视图,程序循环次数较多,但仍能够把基本视图分开。
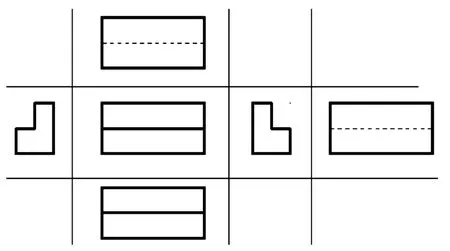
图3 多视图工程图
5 结语
利用黄金分割法适用于离散函数的特点,根据工程三视图的自身特性,建立了适用于黄金分割法的数学模型。该算法不仅可以识别标准三视图,而且可以识别非标准工程图。与其他算法相比,该算法具有运行速度快、效率高、应用范围广的特点。特别是对匹配精度高,几何和拓扑信息完整的三视图尤其有效。该方法可广泛应用于基于工程图的自动重建和识别系统当中,对计算机视觉、工业自动化检测、数控加工、逆向工程及其它计算机辅助设计与制造领域也有一定的参考作用。
在整个三维重建系统中,把视图分割开只是工程图三维重建中的关键一步,基本图元的特征匹配和准确的零部件三维重建才是研究的难点和重点。
[1]傅自钢.基于工程图的三维形体重建方法研究[D].长沙:中南大学,2011:3-5.
[2]张东昌.基于工程三视图的三维智能重建技术的研究[D].大连:大连理工大学,2008:1-3.
[3]史利民,郭复胜,高伟,等.基于语义交互的三维重建[J].计算机辅助设计与图形学学 报,2011,23(5):839-848.
[4]董玉德,赵韩.CAD二次开发理论与技术[M].合肥:合肥工业大学出版社,2009:10-30.
[5]Yan Qingwen,Chen C L P,Tang Zesheng.Efficient algorithm for the reconstruction of 3Dobjects from orthographic projections[J].CAD,1994,26(9):699-717.
[6]张怡文,龚洁晖,张慧.由三视图重建包含圆环面的形体[J].计算机辅助设计与图形学学报,2008,20(2):186-192.
[7]陆国栋,段鹏,彭群生.基于基元组合关系的形体重建技术研究[J].工程图学学报,2007,28(1):48-54.
[8]郑鹏飞,林大钧,刘小羊,等.基于三视图的实体重建技术研究[J].工程图学学报,2011.32(2):49-54.
[9]Furukawa Y,Curless B,Seitz S M,et al.Towardsint internet-scale multi-view stereo[C]//Proceedings of IEEE International Conference on Computer Vision and Pattern Recognition.USA San Francisco:IEEE,2010:1434-1441.
[10]孙靖民,梁迎春.机械优化设计[M].4版.北京:机械工业出版社,2006:9-52.

