面向顶点染色算法的专用指令集优化处理器
杜慧敏,李 萌
(1.西安邮电大学 电子工程学院,陕西 西安710121; 2.西安邮电大学 计算机学院,陕西 西安710121)
图形处理器(Graphics Processing Unit,GPU)的发展主要集中于3D图形渲染领域,如PowerVR、Nvidia、ATI和 BitBoys[1]等产品中都具有3D引擎所必备的高性能染色处理单元。顶点染色器(Vertex Shader)作为GPU的一个重要组成,是高性能染色处理单元不可缺少的部分,主要完成图形处理过程中几何变换、法向量标准化、光照处理等阶段的运算,其性能的提高将有利于改善图形处理器的性能。
目前已经提出的顶点染色器的结构包括:单指令多数据流(Single Instruction Multiple Data,SIMD)、超长指令字(Very Long Instruction Word,VLIW)、VLIW+SIMD、VLIW+SIMD+多线程(Multithreading)以及多核处理机制[2-3]。SIMD 结构通过对功能单元的复制,提高了向量处理的速度,便于实现矩阵运算,但是其对于性能的提高依赖于功能单元的个数,效果有限;VLIW着眼于通过指令级并行提高处理器性能,一条指令往往包含多个操作,虽然它在一定程度上提高了执行效率,但是编译起来比较困难;VLIW+SIMD结合了两者的优点,进一步提高了运算速度,但处理器的复杂度也相应提高;VLIW+SIMD+SMT在VLIW+SIMD基础上加入了SMT技术,充分利用了空闲资源,实现数据处理的并行化,但是硬件复杂度相对较高;多核处理器旨在用多个简单的核实现复杂运算,提高并行性的同时降低了单个内核的复杂度,但是难以对其进行程序的编写。
本文拟在分析顶点染色器功能和常用染色算法基础上,设计一款支持OpenGL命令处理的可编程顶点染色器(Programmable Vertex Shader),引入一种针对顶点染色处理的专用指令集,通过使用该指令集编程实现不同算法的移植,同时,为了提高硬件的运算速度,采用SIMD向量处理、多执行部件的流水结构等技术进行硬件设计。
1 顶点染色器的功能及算法分析
1.1 顶点染色器功能
顶点染色器主要功能是实现几何变换、法向量标准化以及顶点的光照处理。所谓光照处理就是利用一些特定的算法模拟现实世界中物体被光线照射后,反映到人眼中的样子,使最终描绘的场景看起来更加逼真,目前图形界最常用的经典光照模型是 Gouraud模型和 Phong模型[4-5]。
1.2 算法分析
1.2.1 几何变换
几何变换主要完成模型视图变换,通过对图形使用平移、旋转、缩放的操作,将模型坐标系下的图形转换为视图坐标系下的图形,便于在屏幕上显示。这种坐标系间的转换是通过顶点坐标乘以平移、缩放或旋转矩阵来实现的,涉及的矩阵有[6]平移矩阵

缩放矩阵
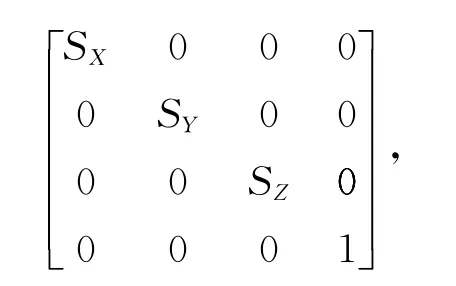
绕X轴旋转矩阵
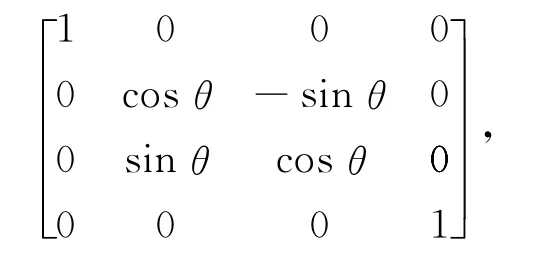
绕Y轴旋转矩阵
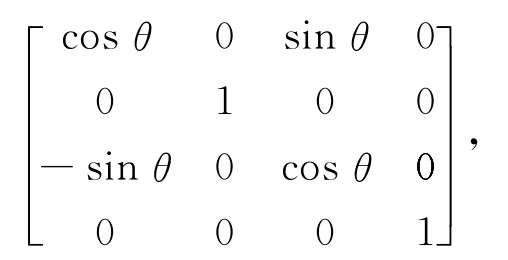
绕Z轴旋转矩阵

1.2.2 法向量标准化
法向量标准化就是将一个长度不为1的法向量单位化,使其变为一个单位法向量[5],即
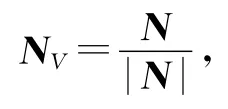
其中N代表归一化前的法向量,|N|代表该法向量的长度,NV代表单位化以后得到的单位法向量。
1.2.3 光照模型
在光照处理的过程中,无论是Gouraud模型还是Phong模型,都需要使用光照方程[5-6]来计算顶点的光照强度,即
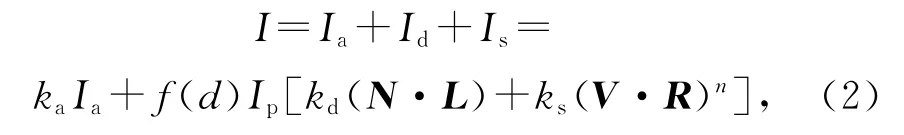
其中I代表拟染色顶点的最终光照强度,Ia代表环境光强度,Id表示漫反射光强度,Is表示镜面反射光强度,Ip代表聚光灯光照强度,ka,kd和ks分别代表环境光系数、漫反射光系数和镜面反射光系数,N代表顶点单位法向量,L代表反射光单位法向量,V代表进入人眼的光的单位法向量,R代表镜面反射光的单位法向量,n代表镜面反射指数,而f(d)为衰减因子,是一个跟光源与顶点的距离d相关的函数[5],即
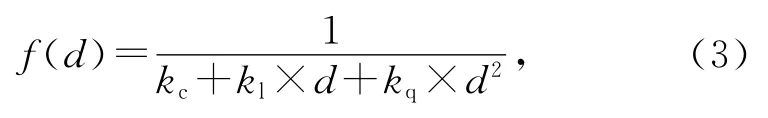
其中d为顶点到光源的距离,kc为常量衰减因子,kl为线性衰减因子,kq为二次衰减因子。
由于实际计算时可能存在多盏聚光灯对顶点进行照射,因此式(2)需要修改为

以将所有的聚光灯的光照结果进行累加,求得顶点的最终光照结果。
对于Gouraud模型,其核心思想是对顶点的法向量和与顶点相邻的多边形的法向量求一个平均值,使用该平均值代替顶点的法向量,并将其代入式(4)计算顶点的最终光照强度。
下面采用类pascal伪代码描述Gouraud模型计算顶点光照的流程,其中PV代表当前拟染色顶点坐标,为一个实数四元组(xV,yV,zV,wV),其中xV,yV,zV分别表示X 轴、Y 轴、Z轴的坐标,wV为齐次因子,通常取1。P1和P2代表与当前拟染色顶点相邻的多边形的另两个顶点,和PV一起构成一个三角形,均为实数四元组,分别表示为(x1,y1,z1,w1)和(x2,y2,z2,w2)。伪代码表示如下。
A:=P1-PV;//得到边〈v,1〉的向量 A(a1,a2,a3)
B:=P2-P1;//得到边〈1,2〉的向量B(b1,b2,b3)
N:=A×B;//求三角形的法向量N(a2b3-a3b2,a3b1-a1b3,a1b2-a2b1)
|N|:=sqrt[(a2b3-a3b2)2+(a3b1-a1b3)2+
(a1b2-a2b1)2];//对三角形法向量 N求模
|NV|:=sqrt(x2,y2,z2);//对PV法向量 NV求模
Nm:=(NV+N)/(|NV|+|N|);//求所有法向量的平均值 Nm,即实数三元组(x,y,z)
cosα:=Nm·L;//代表入射角的余弦值
cosβ:=V·R;//代表入人眼的光和镜面反射光夹角的余弦值
cosnβ:=exp{n ln(cosβ)};
max:=max(cosφ,0);//cosφ为聚光灯切角,代表了聚光灯可以照射的范围
if(max!:=0)//判断一个特定的顶点是否位于光锥的内部
then[It:=It+Ip];//It为所有聚光灯强度的和,初始值为0
else[It:=It]
I:=kaIa+f(d)It(kdcosα+kscosnβ)
与Gouraud模型不同,Phong模型不需要求平均法向量,而是将顶点的法向量直接带入光照方程(4),计算顶点光照强度。该模型下顶点的光照强度计算流程可表示如下。
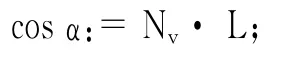
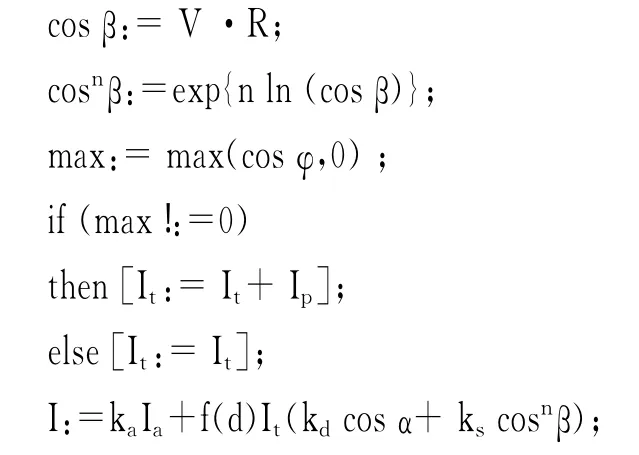
根据以上分析可以看出,Gouraud模型需要先求平均法向量,再计算顶点光照强度,而Phong模型可以根据已知的顶点法向量直接计算顶点的光照强度,似乎Phong模型的计算量更小,但是,对于整个图形绘制的过程来说,Gouraud模型对三角形内部各点采用双线性插值的方法求光照强度,而Phong模型则需要先利用顶点的法向量对三角形内部各点的法向量进行插值,然后逐点代入式(4)进行光照计算,实际上比Gouraud模型计算量更大。不过,Gouraud模型不能很好地反映物体的高光部分,而且由于使用了平均法向量,在图形绘制过程中还可能出现马赫带效应,即在物体表面出现过亮或过暗的条纹。在实际应用中,可以根据不同的需要对两种光照模型进行选择。
1.3 专用指令集定义
根据对算法的分析结果,定义如表1所示的专用指令集并统计指令的使用频度[7-9]。需要注意的是,由于执行单元是多周期的,且很多情况下前面的执行结果需要作为后面操作的输入,因此,在编写程序时需要适当加入空指令NOP。
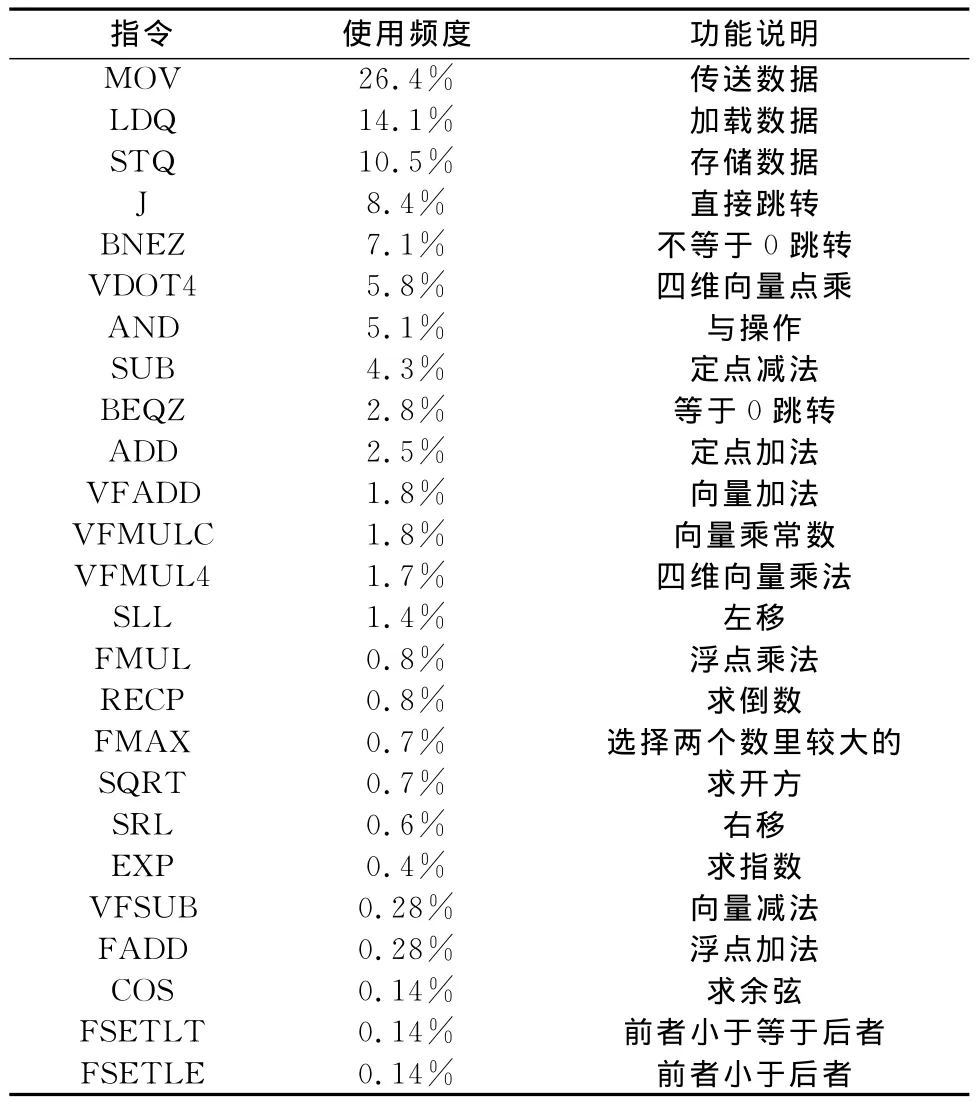
表1 顶点染色器专用指令集
在引入的指令集基础上,制定如下规则。
(1)可编程处理器采用64位固定长度的指令系统,其中低36位为有效指令格式,高28位为保留位,以便今后根据不同需求对指令集进行扩展。
(2)寻址方式包括:立即数寻址、寄存器直接寻址、绝对寻址、寄存器间接寻址四种寻址方式。
2 专用处理器设计
2.1 流水线设计
流水线[7,9]是利用执行指令所需要的操作之间的并行性,实现多条指令重叠执行的一种技术,传统的五级流水线结构如图1所示,包括取指、译码、执行、存储和回写五个阶段。

图1 传统五级流水线结构
采用五级宏流水线结构,如图2所示,包括取指阶段、译码1阶段、译码2阶段、执行阶段和回写阶段。
取指阶段访问指令存储器,获取将要执行的指令;译码阶段1对指令寄存器中的指令进行译码,并通过访问寄存器组获取操作数;译码阶段2根据指令的结构完成执行阶段需要的操作数的选择,产生LDQ和STQ操作访问数据存储器的数据和地址,使得存储访问阶段与执行阶段处于同一执行周期,跳转指令也在本级处理并通过对不同跳转指令产生的跳转PC值进行选择产生新的PC值;执行阶段为多周期操作,包括定点处理单元、浮点处理单元和向量处理单元,执行周期可以从最低的单周期操作到最高的二十多周期操作。回写阶段将计算结果按照指定的规则写入寄存器文件。
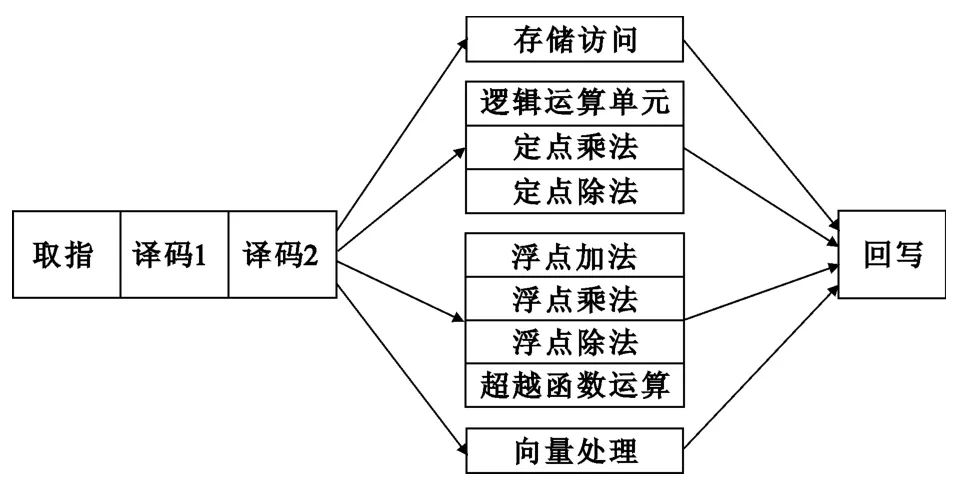
图2 五级宏流水线结构
流水线设计中还采用前递(Forwarding)技术[9],使得前一条指令的计算结果可以直接给下一条指令使用,而不用等到前一条指令将结果写回寄存器后再从寄存器中读取结果,以此缓解数据相关所带来的影响,如图3所示。
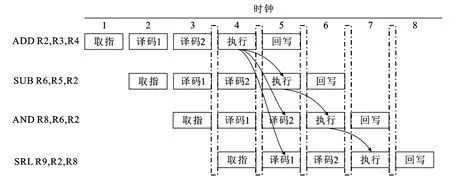
图3 使用前递技术的五级宏流水线
2.2 处理器结构设计
顶点染色器的整体结构如图4所示,共分为四个模块:命令分配器模块、存储管理模块、可编程处理器模块和指令存储结构模块。这四个模块分别完成以下功能。
(1)命令分配器
用于解析来自命令处理器的各种OpenGL命令,按照单参数、环境类、矩阵类、顶点类和透传将不同命令分类;提取命令中的参数并将参数存储于片上数据存储器中;根据不同的命令处理方式启动相应的处理程序;装配并发送新的OpenGL命令。
(2)存储管理
用于管理可编程顶点染色器所涉及的片上数据存储区、统一编址寄存器以及Dcache。
(3)可编程处理器
本模块是一个基于SIMD架构的复杂核处理器,具有五级宏流水线结构;拥有一个向量处理单元、一个标量处理单元和一个特殊函数处理单元;可以处理固定的几何变换和光照程序也可以处理用户自定义的程序[10-13]。
(4)指令存储结构
指令存储区包含了两部分,一部分为固定程序存储区,这部分存储区用于存放固定染色程序;另一部分为Icache存储区,用于存放用户自定义染色程序。
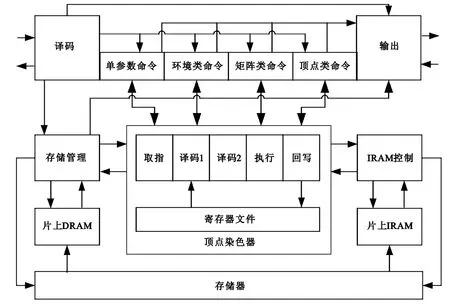
图4 可编程顶点染色器顶层结构
可编程处理器采用程序与数据分离存储的方式,结合五级宏流水线技术,以SIMD结构加速向量类命令处理,以定点和浮点通用结构处理标量类命令,以特殊功能结构加速超越函数处理(图5)。指令序列来源于指令Cache和指令固定程序存储区,数据来源于片上数据存储区和统一编制寄存器。
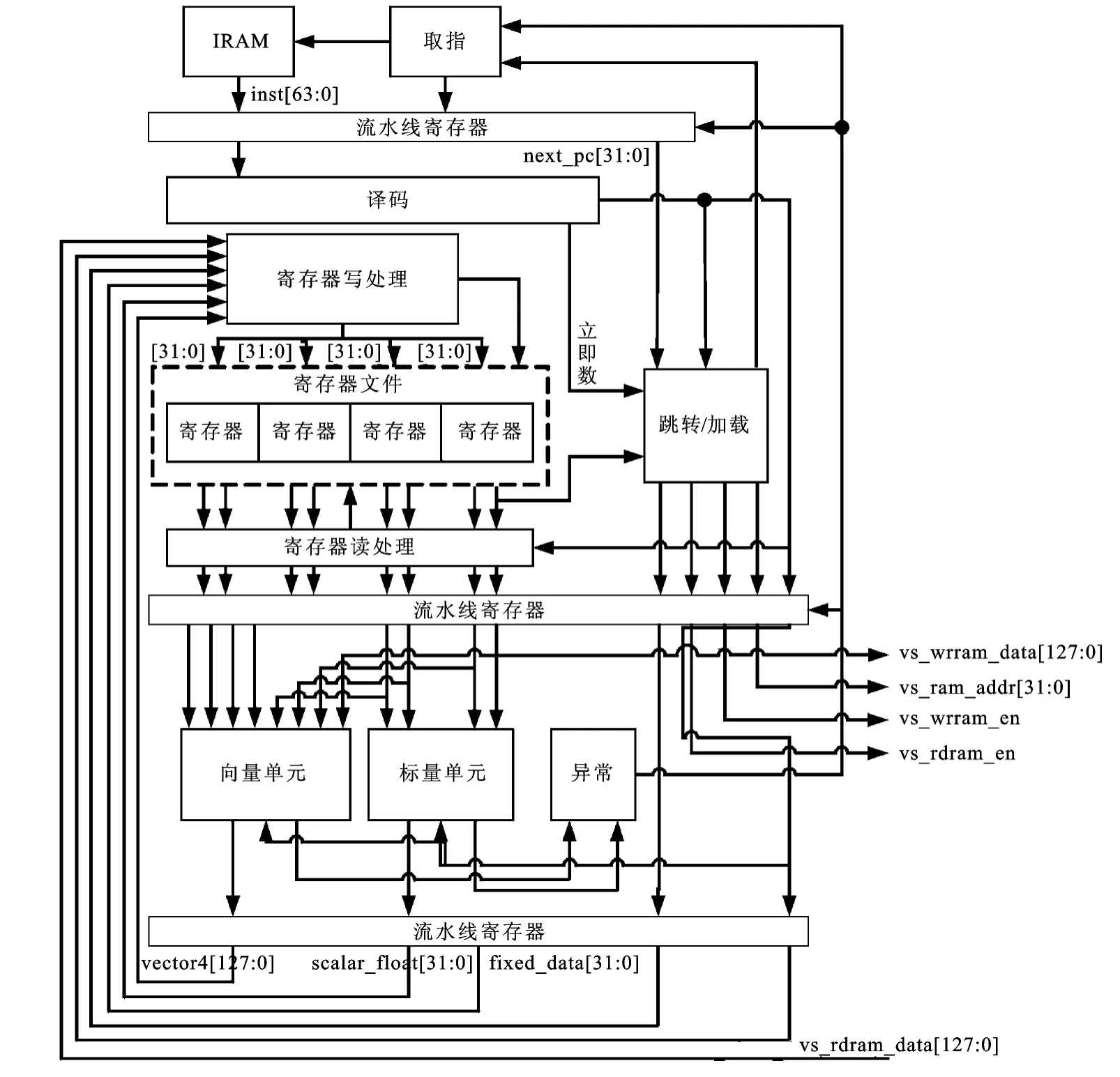
图5 可编程顶点染色器流水线设计
为了加速向量运算,特别设计了4路SIMD架构的向量功能单元,完成向量加减乘运算和向量点乘运算。每组浮点乘法单元和浮点加法单元都拥有4个完全相同的处理单元,根据数据输入时的标记不同,可以分别实现四维向量和三维向量乘法的相关操作,并根据向量指令的目的寄存器选择信号对处理结果进行重新分配。这样的结构可以大大缩短向量计算花费的时钟周期数,以四维向量的乘法为例,如果不采用SIMD架构,需要做4次浮点乘法,共花费28个周期,而在SIMD架构下可以同时做4个浮点乘法,7个时钟周期就可以得到结果,具体结构如图6所示。

图6 向量处理单元设计
除了采用SIMD结构外,处理器还拥有一个特殊函数运算单元来实现超越的运算。该单元采用CORDIC算法,通过对参数的设置,使用简单的移位操作和加法运算,以迭代的方式,实现复杂的超越函数运算,便于硬件实现,精度较高[14]。在保证设计需求的前提下,将浮点特殊函数运算单元采用浮点数-定点数转换模块和具有串行迭代结构的定点CORDIC单元实现,迭代次数为13次。由于使用定点加法器代替浮点加法器完成迭代过程中的加法操作,每一次迭代都减少了4个时钟周期(本设计中浮点加法花费5个时钟周期,定点加法在1个时钟周期内就可以完成),减少了运算周期数,提高了运算速度。
3 仿真结果及分析
3.1 仿真结果
本设计采用SystemVerilog搭建验证平台,在工作站上使用Linux环境下QuestaSim6.5b作为仿真工具,使用基于JAVA的图形转换软件对生成的数据进行图形绘制。整体功能验证平台如图7所示,该验证平台具有自动对比功能,包含输入单元、输出单元、参考模型和DUT四个部分。
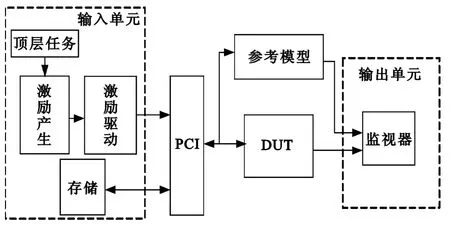
图7 整体功能验证平台
采用不同图形仿真所得结果如图8所示。可以看出,可编程顶点染色器功能正确,可以完成对顶点的染色处理,绘制出真实的图形。

图8 仿真结果
3.2 性能分析
采用Xilinx公司Virtex6-760对可编程顶点染色器电路进行逻辑综合,综合报告如图9所示,占用了3%的LUT以及1%的Slice寄存器,资源消耗适中。

图9 电路综合报告
电路的最大工作频率为197MHz,不加光照的情况下,可编程顶点染色器处理一个顶点大约需要40个周期,顶点处理能力达到5Mvertexx/s,能够满足设计要求。
4 结语
设计了一种基于SIMD架构的可编程顶点染色器,定义了专用的指令集,更适于进行向量类操作,不仅提高了顶点染色的速度,而且可编程的设计也提高了顶点染色器的灵活性,通过程序的移植,能够实现除顶点染色算法之外的其他算法。
[1]Moya V,Gonzalez C,Roca J,et al.A Single(Unified)Shader GPU Microarchitecture for Embedded Systems[C]//Proceedings of 1st International Conference on High Performance Embedded Architectures and Compilers(HiPEAC 2005).Spanish Barcelona:Springer-Verlag,2005:286-301.
[2]Lee Y,Avizienis R,Bishara A,et al.Exploring the tradeoffs between programmability and efficiency in data-parallel accelerators[C]// Proceedings of 38th Annual International Symposium on Computer Architecture(ISCA 2011).US CA San Jose:Institute of E-lectrical and Electronics Engineers Inc, 2011:129-140.
[3]李涛,肖灵芝.面向图形和图像处理的轻核阵列机结构:萤火虫2号[J].西安邮电学院学报,2012,17(3):41-47.
[4]Edward Angel.交互式计算机图形学:基于OpenGL的自顶向下方法[M].吴文国,译.4版.北京:清华大学出版社,2007:255-288.
[5]Shreiner D.OpenGL编程指南[M].李军,徐波,刘金华,等译.7版.北京:机械工业出版社,2010:123-148.
[6]孙刚德.基于自动线程和超长指令的统一架构着色器的设计研究[D].杭州:浙江大学电气工程学院,2012:11-15.
[7]Aasaraai K.,Moshovos A..Design Space Exploration of Instruction Schedulers for Out-of-Order Soft Processors[C]//Proceedings of 2010International Conference on Field-Programmable Technology(FPT’10).China Beijing: IEEE Computer Society, 2010:385-388.
[8]Munoz D M,Sánchez D F,Llanos C H,et al.Tradeoff of FPGA Design of Floating-point Transcendental Functions[C]//Proceedings of 17th IFIP International Conference on Very Large Scale Integration(VLSI-SoC 2009).Brazil Florianopolis:IEEE Computer Society,2011:239-242.
[9]胡伟武,陈云霁,肖俊华,等.计算机体系结构[M].北京:清华大学出版社,2011:55-139.
[10]Kubosawa H,Higaki N,Ando S,et al.A 2.5-GFLOPS,6.5Million Polygons per Second,Four-Way VLIW Geometry Processor with SIMD Instructions and a Software Bypass Mechanism[J].IEEE Journal of Solid-State Circuits,1999,11 (34):1619-1625.
[11]Jones A K,Hoare R,Kourtev I S,et al.A 64-way VLIW/SIMD FPGA Architecture and Design Flow[C]//Proceedings of 11th IEEE International Conference on Electronics,Circuits and Systems(ICECS 2004).Isreal Tel Aviv:Institute of Electrical and E-lectronics Engineers Computer Society, 2004:499-502.
[12]Hennessy J L,Patterson D A.计算机体系结构:量化研究方法(影印版)[M].4版.北京:机械工业出版社,2010:A2-B47.
[13]韩俊刚,蒋林,杜慧敏,等.一种图形加速器和着色器的体系结构[J].计算机辅助设计与图形学学报,2010,22(3):363-372.
[14]李全.浮点反正切函数的FPGA实现[J].电子技术应用,2010,36(8):9-10.

