有色噪声条件下的卡尔曼滤波
陈 方,吴小役,刘文逸,刘 芳
(西北机电工程研究所 第六研究室,陕西 咸阳712099)
卡尔曼(Kalman)滤波技术[1]诞生于20世纪60年代,是现代控制理论发展过程中产生的一种最优估计技术,是在动态噪声和观测噪声均为白噪声条件下推导出来的。其核心思想[2]是根据当前数据和前一时刻的诸量估计值,依据递推公式,计算出新的诸量估计值。卡尔曼滤波实际是对随时间变化的参数估计的一种顺序最小二乘逼近,特别适用于动态测量。
目前,卡尔曼滤波技术已经广泛应用在导航,数据融合技术,控制技术等领域,特别是在计算机图像处理方面,脸部识别,图像边缘处理中大都采用卡尔曼滤波技术[3]。而在实际工程当中,经常会遇到有色噪声。对于卡尔曼滤波,需要同时考虑有色动态噪声和有色观测噪声的双重影响。现有的处理方法,大都是采用白噪声驱动下的有色卡尔曼滤波技术,就是将有色噪声进行白化处理,即表达成白噪声函数[4],再进行滤波。或者通过差分、差分组合或加大采样间隔的方法来消除或减弱动态序列的有色噪声影响,若要减弱有色观测噪声,采用增广状态方程,即将有色噪声作为模型状态参数,与更正的状态参数一起求解[5-6]。这样也很难消除有色噪声的影响,还可能会造成滤波发散或者结果失真。
在卡尔曼滤波基本方程的基础上,通过增加计算噪声相邻历元间的协方差,利用线性变化,推导出了有色噪声条件下的卡尔曼滤波方程,最后通过Matlab仿真进行验证。
1 卡尔曼滤波技术及有色噪声
卡尔曼滤波技术的原理是考虑一个随时间变化的参数向量(即状态向量),通过一个线性系统(即观测方程),可以测得一组在不同时刻下与参数相对应的参数值。如果能够建立一个参数的确定性和不确定性随时间变化的模型(即系统模型),卡尔曼滤波就可以在任何时刻下对状态矢量进行估计,而且,它对状态矢量的估计是无偏的,方差最小的。
线性随机系统[1]

式中xk+1为k+1时刻的状态向量,νk为k时刻系统观测量。Ak、Γk和Ck分别是n×n、n×p、q×n已知常值矩阵,且1≤p,q≤n。基于初始条件E(x0)和D(x0),xk的线性无偏最小方差估计
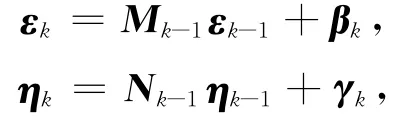
式中
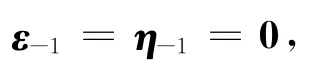
且{βk}和{γk}是不相关的零均值高斯白噪声序列,满足
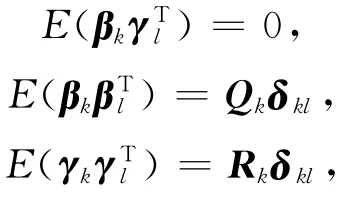
其中Mk-1和Nk-1为已知的p×p和q×q常值矩阵。若噪声序列{εk}和{ηk}满足上述条件,则称为有色噪声过程[1]。
2 有色动态噪声的处理
卡尔曼滤波是基于系统的动力学模型和观测序列来求解状态向量估计的算法,其函数模型和随机模型为[1]
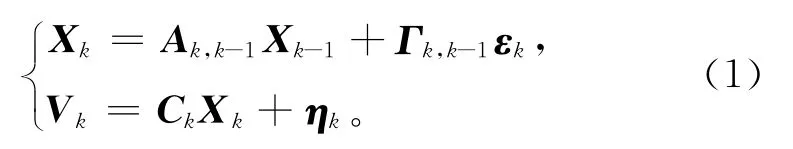
已知
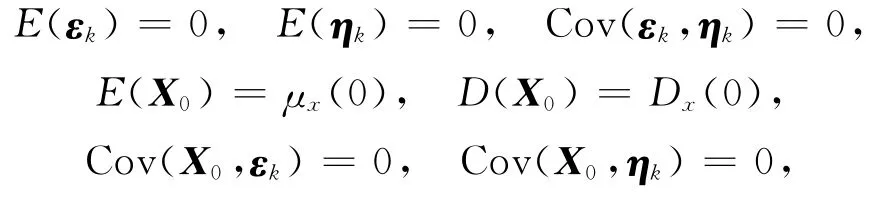
其中Xk为k时刻的系统状态,Ak为系统参数阵,Γk为噪声驱动阵,εk为动态噪声,Vk为k时刻实际量测值,Ck为量测系统参数阵,ηk为观测噪声。
卡尔曼滤波基本方程[1]
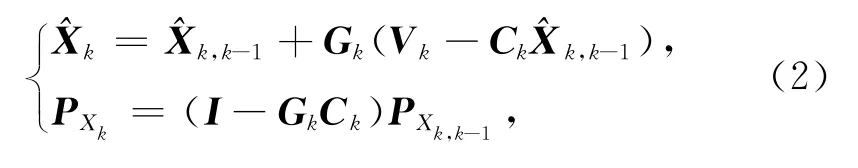
式中
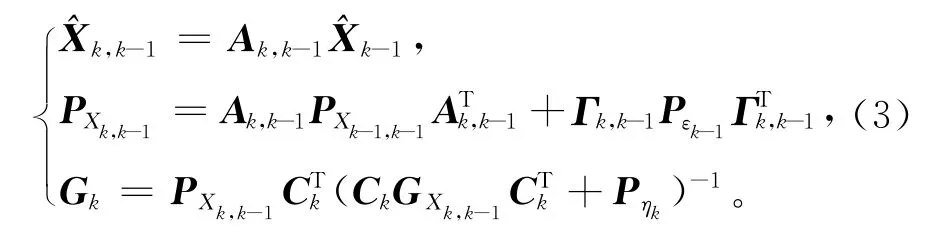
在方程中,εk和ηk为互不相关均值为零的白噪声。是滤波估计值,是一步预测量,PXk是协方差更新矩阵,PXk,k-1是一步预测协方差矩阵,Gk是状态增益阵。
若动态噪声εk和εj的协方差不等于零,则εk、ε2、…、εn为有色噪声序列。考虑动态噪声εk与相邻历元噪声εk-1、εk+1相关,不相邻的历元噪声不相关,则动态噪声的协方差矩阵为分块三对角矩阵

其中a1,a2,…,an-1为相邻历元动态噪声间协方差值。
假设卡尔曼滤波基本方程初始状态
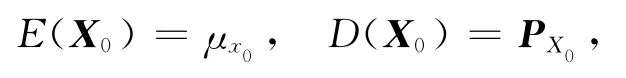
且X0与{εk},{ηk}都不相关。测量k-1次后,可得到的估计值,根据动态方程可以预测第k次计算的状态值。因为E(εk)=0,则的一步预测合理值为
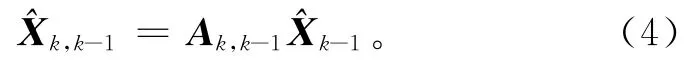
假设
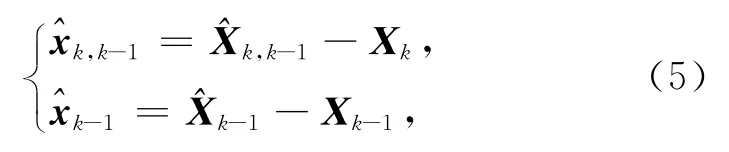
式(4)两边减去Xk即

可得

则有
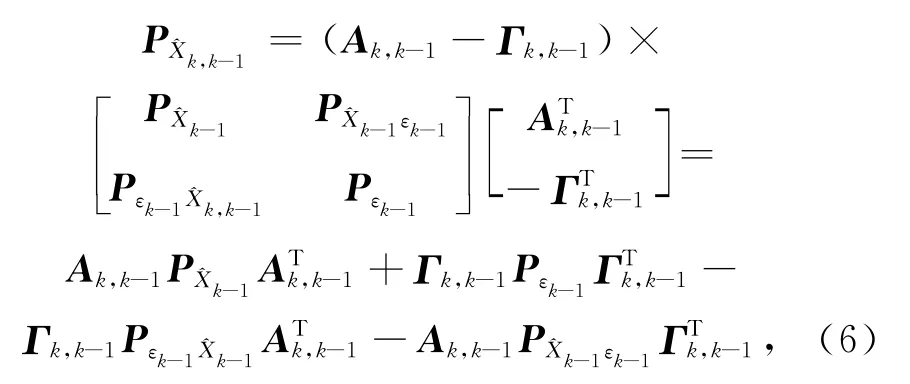
由于


则式(7)中

有色噪声滤波公式就化为白噪声条件下的卡尔曼滤波公式。因此可以认为,动态噪声为白噪声条件下的卡尔曼滤波是动态噪声为有色噪声条件下卡尔曼滤波的特殊情况。
3 有色观测噪声的处理
如果观测噪声的协方差不为零,则观测噪声为有色噪声序列,假设卡尔曼滤波的观测方程为[7]
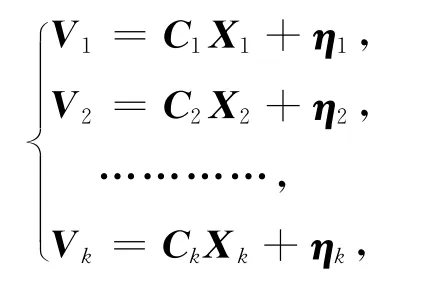
其中Vk为k时刻实际量测值,Ck为量测系统参数阵,ηk为观测噪声。
对于观测噪声为有色噪声的卡尔曼滤波,假设系统的动态噪声和观测噪声均值为零,互不相关,动态噪声εk为高斯白噪声,ηk为有色噪声序列,因而与ηk相关,由式(3)可得其协方差为[8]

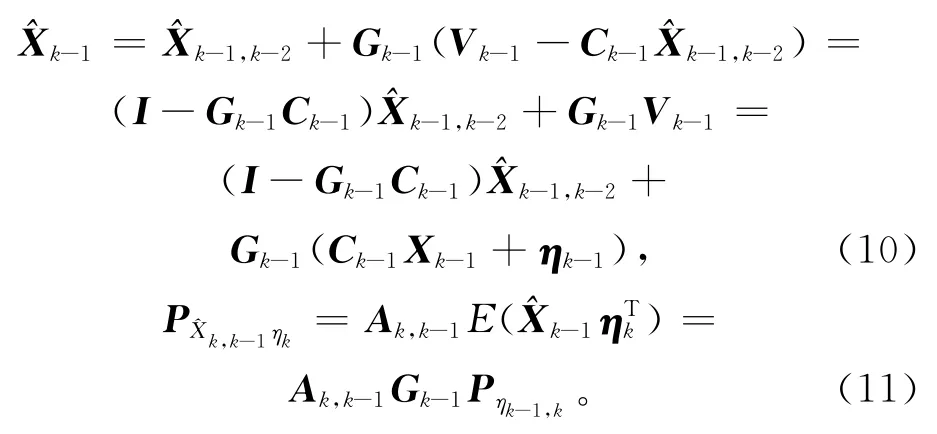
PXk,k-1ηk为k时刻下一步预测量与观测噪声间协方差。
考虑到相邻历元观测噪声相关的卡尔曼滤波公式为[9]
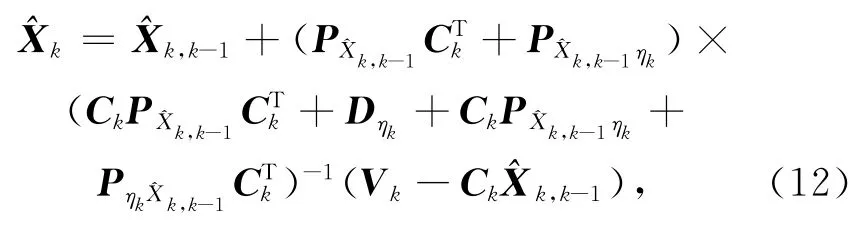
若设
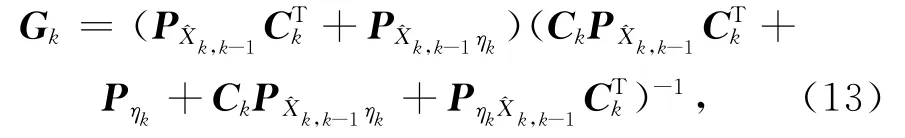
则式(12)可以化简为
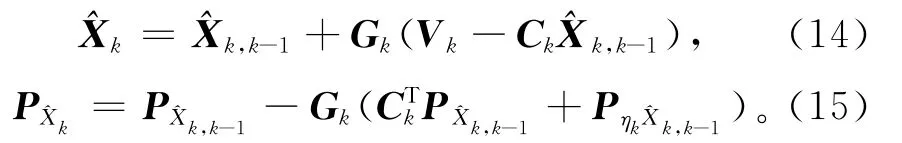
在式(11)中,当观测噪声为白噪声时,有

于是

此时,方程式退化为白噪声条件下的卡尔曼滤波公式。可见,观测噪声为白噪声条件下的卡尔曼滤波是观测噪声为有色噪声条件下卡尔曼滤波的特殊情况。
结合上面两种方法,就可以得到在动态噪声和观测噪声都是有色噪声情况下的处理方法,即有色噪声条件下的卡尔曼滤波。
4 仿真分析
利用Matlab软件进行仿真。给定周期为150s,幅值为1的正弦信号s作为系统输入信号,假设系统参数阵Ak、噪声驱动阵Γk、量测系统参数阵Ck均为1阶单阵,在动态噪声和观测噪声均为均匀白噪声和有色噪声的两种情况下,分别利用传统卡尔曼滤波和本文推导的有色噪声条件下相邻历元噪声相关的卡尔曼滤波方法进行滤波处理,并在同一个界面中,对相同信号的两种处理结果进行了对比。仿真结果分别如图1,图2所示。
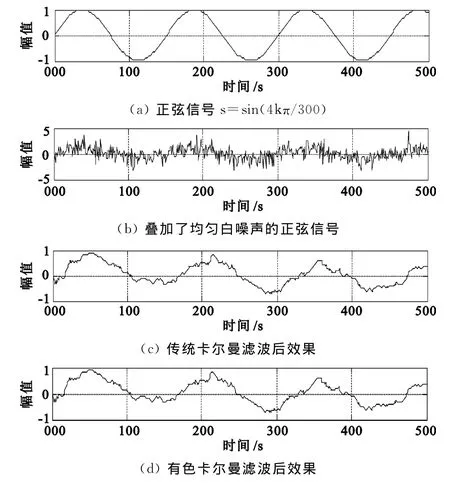
图1 白噪声作用下的卡尔曼滤波
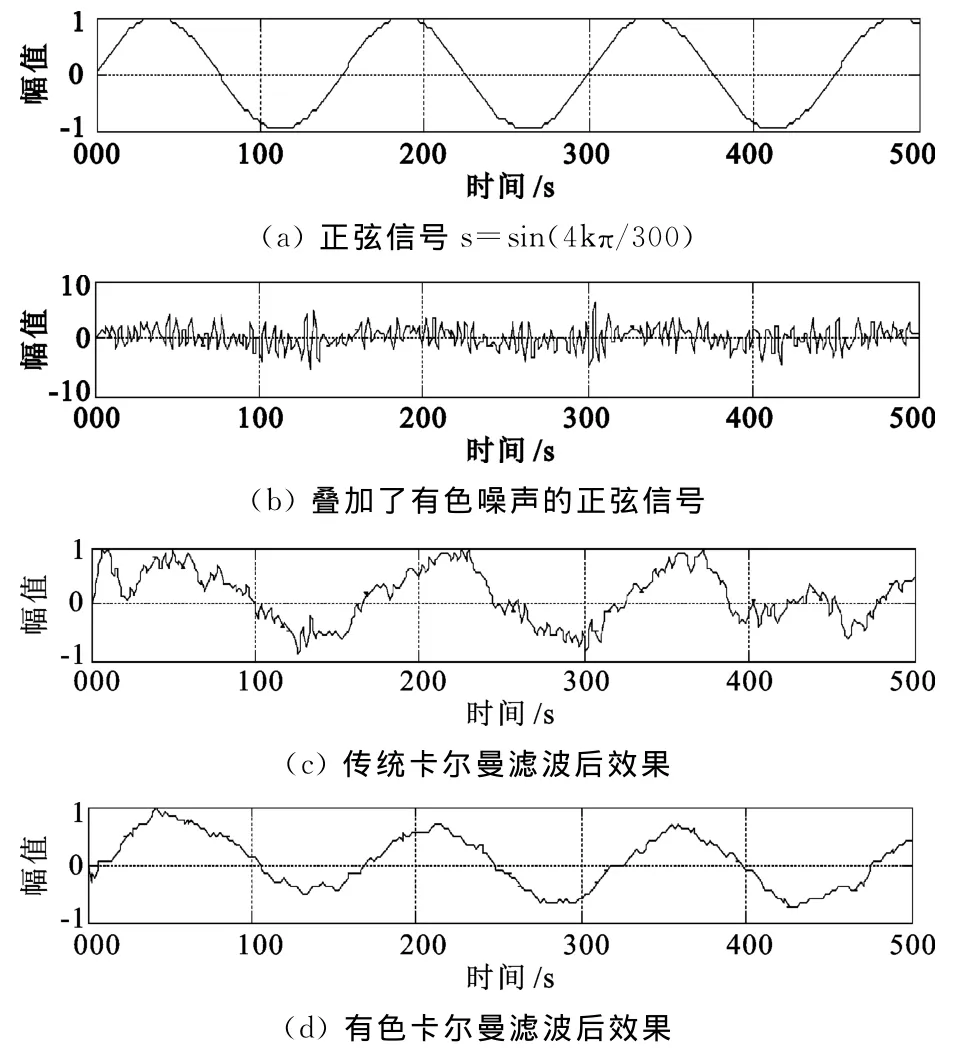
图2 有色噪声作用下的卡尔曼滤波
在图1和图2中,第一条曲线为输入的正弦信号;第二条曲线为叠加了噪声后的正弦信号,第三条曲线为利用传统卡尔曼滤波方法处理后的效果;第四条曲线为利用有色噪声条件下卡尔曼滤波方法处理后的效果。其中图1是对叠加了均匀白噪声的正弦信号进行的两种卡尔曼滤波处理,图2是对叠加了有色噪声的正弦信号进行的两种卡尔曼滤波处理。
由图1可以看出,当噪声信号为白噪声时,由于白噪声相邻历元之间无相关性,则传统的卡尔曼滤波与有色噪声条件下卡尔曼滤波对信号的处理效果相同,证实了当噪声信号为白噪声时,有色噪声条件下的卡尔曼滤波公式退化为白噪声条件下的卡尔曼滤波公式。
由图2中可以看出,当噪声信号为有色噪声时,利用传统卡尔曼滤波的方法,将有色噪声当作白噪声来处理,处理结果误差较大,效果不理想,而利用有色噪声条件下的卡尔曼滤波方法,处理后的信号曲线更为平滑,误差减少。可见,通过对同一信号叠加不同噪声,再对比两种卡尔曼滤波方法处理的结果,证实了白噪声条件下的卡尔曼滤波是有色噪声条件下卡尔曼滤波的特殊情况,并且有色噪声条件下的卡尔曼滤波方法优于传统的卡尔曼滤波方法,对噪声的处理效果更佳。
5 结论
依据有色噪声相邻历元间噪声相关的特点,推导出了有色噪声条件下的卡尔曼滤波方程,通过仿真实验,证明改进的方法可以减小计算误差,有效避免滤波发散和结果失真,对于处理有色噪声信号,效果更佳。
[1]崔锦泰,陈关荣.卡尔曼滤波及其实时应用[M].北京:清华大学出版社,2013:58-63.
[2]秦永元,张洪钺,汪叔华.卡尔曼滤波与组合导航原理[M].西安:西北工业大学出版社,1998:128-129.
[3]张建军.基于改进的扩展卡尔曼滤波伺服系统建模技术研究[J].计算机应用研究,2012,29(3):944-946.
[4]赵长胜.有色噪声观测量的主次静态滤波与配置[J].测绘通报,2004(4):17-18.
[5]张金槐,蔡洪.飞行器试验统计学[M].长沙:国防科技大学出版社,1995:161-182.
[6]白辉,卢光跃,王晓侃.非信任环境中一致卡尔曼滤波的数据融合算法[J].西安邮电学院学报,2012,17(5):10-14.
[7]宋国东,姜守达,林连雷.复杂有色噪声广义系统信息融合 Kalman滤波器[J].仪器仪表学报,2013,34(5):1195-1200.
[8]唐斌,陈金平,杨龙,等.基于有色噪声卡尔曼滤波算法在电力系统母线的GPS多径估计研究[J].北京理工大学学报,2010,30(10):1197-1225.
[9]崔希璋.广义测量平差[M].武汉:武汉大学出版社,2005:219-287.

