有效亮度温度测量中发射率影响的修正
原遵东, 邢 波, 柏成玉, 傅承玉, 陈桂生
(1.中国计量科学研究院,北京 100029; 2.湖北省计量测试技术研究院,湖北武汉 430223;3.中国测试技术研究院,四川成都 610021)
有效亮度温度测量中发射率影响的修正
原遵东1, 邢 波1, 柏成玉1, 傅承玉2, 陈桂生3
(1.中国计量科学研究院,北京 100029; 2.湖北省计量测试技术研究院,湖北武汉 430223;3.中国测试技术研究院,四川成都 610021)
经典的短波高温修正模型不适用于中长波红外温度计的发射率修正和不确定度评定。采用有效亮度温度概念,得到了对于温度范围和测温波长具有广泛适用性的发射率影响模型以及具有简明物理含义的微差近似形式,包含了经典亮度温度理论中的发射率影响修正和环境辐射误差修正。定量分析了经典的短波高温修正模型的误差。针对黑体辐射源的不同溯源方法,讨论了辐射温度计校准中的发射率影响修正方法,并给出修正实例。所用方法可用于辐射测温应用、辐射温度计校准和黑体辐射源校准中的发射率和环境影响修正以及辐射源发射率不确定度对校准结果不确定度贡献的计算。
计量学;发射率修正;有效亮度温度;辐射温度计;黑体辐射源;校准;不确定度
1 引 言
在辐射温度计的发展历程中,可见光波长的光学高温计和宽带的辐射感温器是典型的温度计,用于高温测量。在教科书中,被测物体发射率对测温的影响分析计算,常将前者视为单色温度计,采用Wien公式;将后者近似视为全辐射温度计,采用Stefan-Boltzmann辐射定律。
辐射测温的直接结果是以理想黑体特性表示的表观温度,被测对象的实际温度需要经发射率影响修正才能得到。因此,发射率修正是辐射测温应用的普遍需求。
随着辐射测温技术,特别是红外测温技术的发展,广泛应用的8~14μm宽带辐射温度计普遍能测量到0℃以下,而最大允许误差(或准确度)从典型的±1%到±0.75%乃至±0.5%;黑体辐射源(辐射源)的宣称有效发射率(以下简称发射率)从早期的0.98~0.99提高到典型的0.995,不低于0.998的也属常见。然而,已有辐射温度计规程JJG 856—94、JJG 415—2001和JJG 67—2003[1~3]在检定数据处理中均不修正辐射源发射率偏离1对检定结果的影响,在以往的不确定度分析中仅采用忽略环境辐射影响的高温测量模型。根据不确定度分析,规程对辐射源的技术要求用于检定1%级的8~14μm辐射温度计时远不够理想,特别是对发射率的技术要求。如在1 000℃时0.99的发射率对8~14μm温度计检定结果的影响约为7.5℃[4]。
目前正在起草中的辐射温度计新检定规程拟适当提高对辐射源发射率的技术要求,同时对发射率偏离1的影响进行修正。黑体辐射源有效发射率影响的修正及其不确定度评定是辐射测温计量中的关键因素之一。国际温度咨询委员会辐射测温工作组(CCT—WG5)发表了对银点以上温区的基标准级辐射温度计和银点以下温区标准级辐射温度计的校准不确定度评定指南[5,6],包含对发射率在经典亮度温度的影响修正和环境辐射反射的修正[6,7]。本文针对辐射温度计的检定或校准(以下简称检定),利用有效亮度温度概念,阐述辐射测温检定校准应用中的发射率修正,特别是采用不同量值溯源方式的辐射源时对发射率的修正方法。
2 辐射源的溯源方式
从技术合理性考虑,应要求辐射温度计检定结果的不确定度不超过被检温度计最大允许误差的1/3,但实际情况难以达到;即使要求标准装置的传递量值(辐射温度、亮度温度或比色温度)的不确定度不超过被检温度计最大允许误差的1/3,也部分地存在困难;仅要求标准温度计的不确定度不超过被检温度计最大允许误差的1/3(JJG 856为1/5,JJG 415为1/3,JJG 67略低于1/3),虽然是受当时条件的制约,但对有效控制辐射源引入的不确定度和引导计量部门建立具备更合理的不确定度水平的计量标准装置不利,对理解不够的读者有误导。现行规程对辐射源发射率的最高要求为1±0.005,对8~14μm辐射温度计检定结果的影响在1 000℃约为3.7℃,对于±1%最大允许误差的温度计已超过最大允许误差绝对值的1/3。因此,中国计量科学研究院已尝试进行辐射源的多波长(或波段)亮度温度校准,并正在建立新的标准辐射源组以提高辐射源校准水平。
新的溯源方式将辐射源(或与参考温度计的组合)视为计量器具,溯源方式为:(1)以接触式温度计为参考温度计;(2)以辐射温度计为参考温度计;(3)辐射源多波长(波段)亮度温度溯源。方式(2)和方式(3)将有效减小或基本上消除发射率偏离1的影响[8]。上述溯源方式将纳入新制定的辐射温度计检定规程,并且需要根据不同溯源方式和被检辐射温度计类型确定发射率影响修正方法。
3 发射率修正
3.1 辐射温度计的测温模型
辐射测温的理论基础是Planck黑体辐射定律
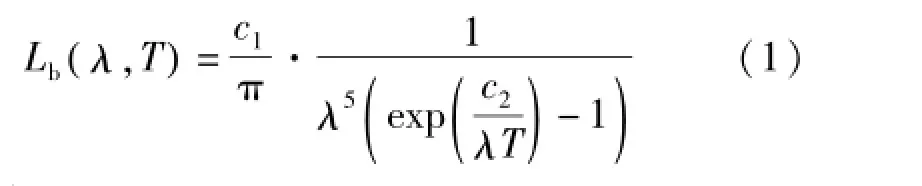
式中,Lb(λ,T)为黑体在波长λ和温度T的光谱辐射亮度;c1为第一辐射常数;c2为第二辐射常数,c2=0.014 388 m·K。
在存在环境辐射的条件下,单一带通辐射温度计测量的是有效亮度温度(或有效积分亮度温度)[9,10],是对经典亮度温度和辐射温度的概念扩展,以下简称亮度温度。由于发射率偏离1,黑体辐射源的亮度温度有别于其实际温度。本文以下分析基于均匀环境温度条件的室内测量,通常可将室内环境亮度近似视为环境温度下的黑体辐射亮度。黑体辐射源的亮度温度与实际温度和环境温度的关系为
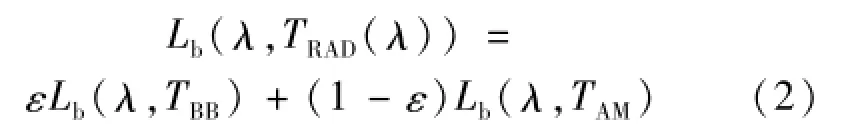
式中,TRAD为黑体辐射源在波长λ下的亮度温度;TBB为黑体辐射源实际温度;TAM为环境温度,ε为黑体辐射源发射率。
辐射源在波长λ的亮度温度为
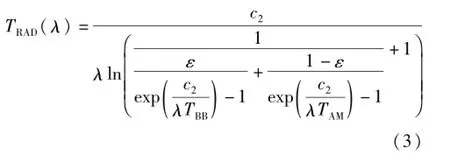
实际单带通辐射温度计的测温模型是对温度计光谱响应度的波长积分形式[4],计算较复杂。为简化计算、便于推导,对于窄带温度计,式(2)中的λ可用其中心波长表示;对于宽带温度计,可用有效波长(等效波长)[11]表示。
有效波长与发射率有关。对于发射率明显小于1的灰体,有效波长与极限有效波长的差异较小,一般在±1%以内[11]。对于黑体辐射源的发射率修正,有效波长可用极限有效波长近似表示。极限有效波长是温度计的特性。基于矩形光谱响应模型[11]计算了在-60~1 500℃下的2种常见光谱范围宽带辐射温度计的极限有效波长,并以Sakuma方程[12]中经典的波长项形式λ=A+B/(t+273.15),对上述计算结果拟合的最大相对偏差均小于±1%,结果见表1。8~14μm温度计的极限有效波长约为10μm,而非中心波长为11μm。Sakuma和Saunders讨论了适用于宽带温度计的Sakuma方程的更复杂的波长形式[6,13],但用于小温差修正,本拟合形式即可获得足够准确的结果。
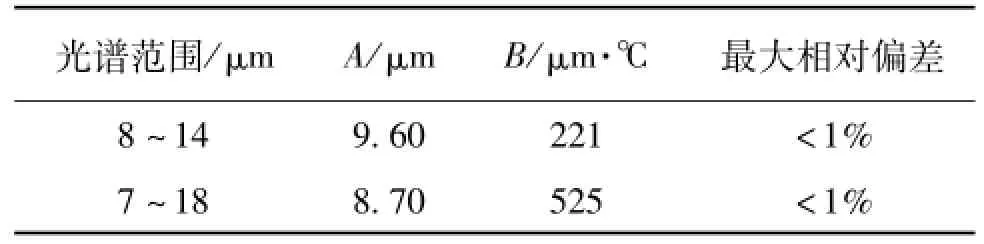
表1 宽带辐射温度计的极限有效波长拟合系数
3.2 亮度温度偏离实际温度
文献[6,7]基于经典亮度温度概念,分别修正发射率误差和环境辐射反射误差。本文利用有效亮度温度的概念,利用式(3)直接计算亮度温度偏离实际温度的程度
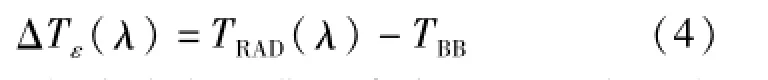
在辐射温度计检定的典型条件——环境温度20℃、发射率0.995下,基于式(3)和式(4)的典型计算结果见表2。发射率向小于1的方向偏离对亮度温度偏离辐射源实际温度的影响在TBB大于、等于、小于TAM时分别小于、等于、大于0℃,这与对经典亮度温度的影响(恒小于0℃)不同,绝对值随偏离环境温度的程度而增大,在环境温度以上随波长增大而增加,在环境温度以下随波长增大而减小。
3.3 简化的近似公式及其适用性
合理简化的公式利于定性理解、方便计算、减少错误,用于检定规程的计算方法是有意义的,特别是用于不确定度分析与计算。然而,了解其适用条件和近似引起的误差是必要的。
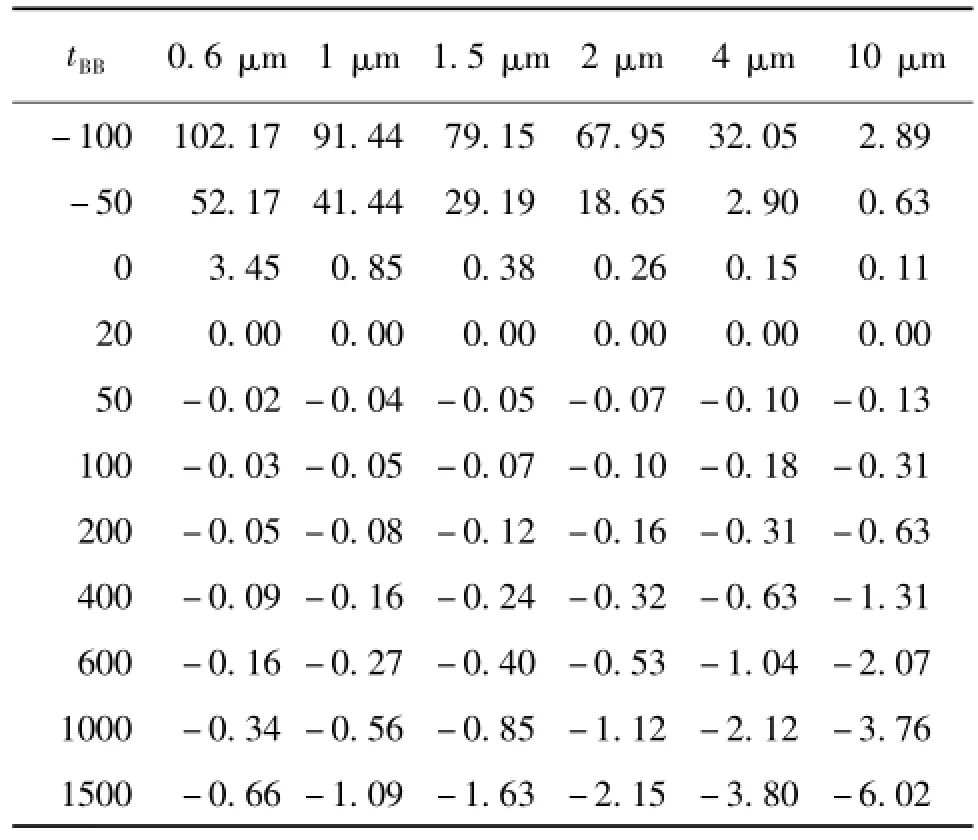
表2 典型条件下ΔTε(λ)基于式(3)和(4)的计算结果℃
经典亮度温度理论中,发射率对亮度温度的影响广泛采用Wien近似得到的公式进行计算
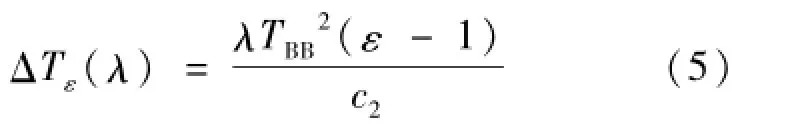
但随着红外测温范围的下延,常被沿用到非短波高温测量中的发射率修正与不确定度评定。表3列出式(5)与准确公式(4)之比,以说明式(5)的适用性,比值越接近1说明越准确。表中的斜体数据为因忽略环境辐射引起的误差超过±1%的区域,下划线数据为Wien近似引起的误差超过1%的区域。对于长波温度计,如8~14μm温度计,由于既忽略环境辐射又采用Wien近似,使式(5)对所有温度范围均不适用,其相对误差在1 000℃达到50%。
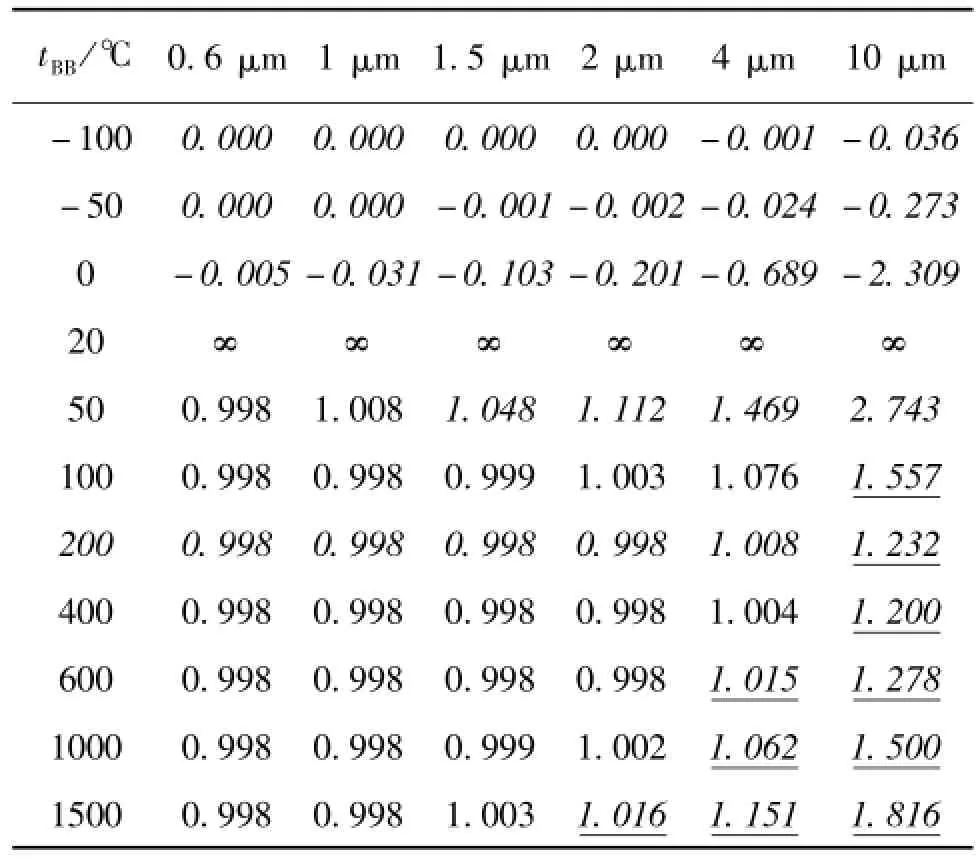
表3 环境温度为20℃辐射源发射率为0.995时不同温度波长下式(5)与式(4)的比值
根据式(4)得到微差形式的近似式
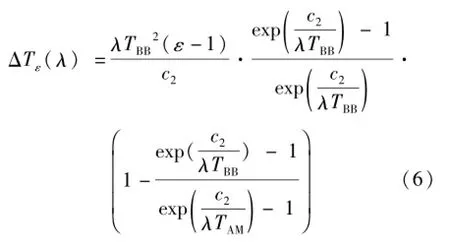
式中,等号右侧为3项因子形式,依次为式(5)等号的右侧项(与波长、温度的平方和发射率偏离1的程度成正比)、Planck修正项和环境辐射修正项(环境温度下为0,大于环境温度时大于0,小于环境温度时小于0)。此微差形式公式的突出优点是物理含义明显、易于理解与记忆,且因近似引起的不适用性很有限。
4 辐射温度计检定中的修正计算
为了对不同情形使用统一的公式表达,将辐射源发射率偏离1引起检定结果(被检温度计固有误差)的偏差ΔTVε分解为以参考值表示辐射源实际温度引起的误差ΔTSε和以被检温度计测量的亮度温度或比色温度示值表示辐射源实际温度引起的误差ΔTTε这2部分:
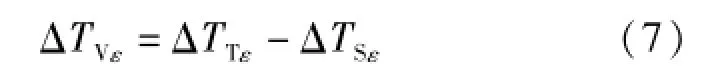
在确定固有误差(或校准示值误差)时,应减去ΔTVε修正黑体辐射源发射率偏离1的影响。
4.1 ΔTSε的计算
采用接触式参考温度计时,其测量结果表示的就是辐射源实际温度,故ΔtSε=0℃。
以标准器(辐射温度计或辐射源)在波长λS的亮度温度表示辐射源实际温度所引起的误差ΔTSε为
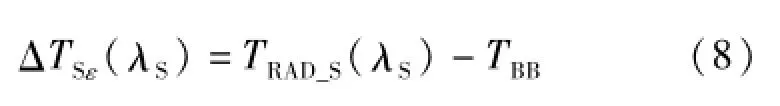
4.2 ΔTTε的计算
本文假设辐射源发射率的光谱选择性可忽略,即被检温度计为比色温度计时,比色温度等于辐射源实际温度,故ΔtTε=0℃。
被检辐射温度计为极限有效波长为λT的单带通辐射温度计时,以辐射源实际温度表示被检辐射温度计测量的亮度温度引起的误差ΔTTε为
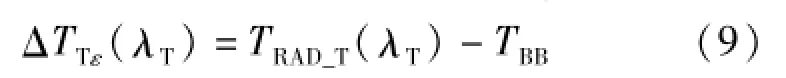
4.3 分类汇总
上述参考标准器和被检温度计类型下的ΔTVε的汇总表见表4。本文以标准器实际温度传递被检辐射温度计量值的思路分别给出发射率偏离1引起的标准器和被检温度计误差,是为了对不同的标准器溯源方式和不同类进行被检温度计给出统一形式的计算方法,便于比较,实际应用可直接用式(7)合并计算。

表4 计算ΔTVε汇总表
4.4 修正实例
在400℃校准一支8~14μm辐射温度计。所用黑体辐射源的发射率为0.995±0.003,标准值分别为辐射源在8~14μm的亮度温度校准数据、4 μm辐射温度计的亮度温度和精密铂电阻温度计的校准数据。被校辐射温度计在3种情形下的数据处理见表5。
需要注意的是,发射率的不确定度对标准辐射温度计和被校辐射温度计的影响是完全正相关的,两不确定度分量应按代数方法合成
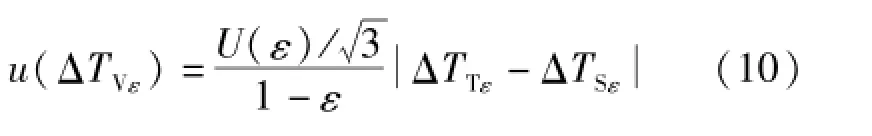
再与其他互不相关分量按不确定度传播率合成。
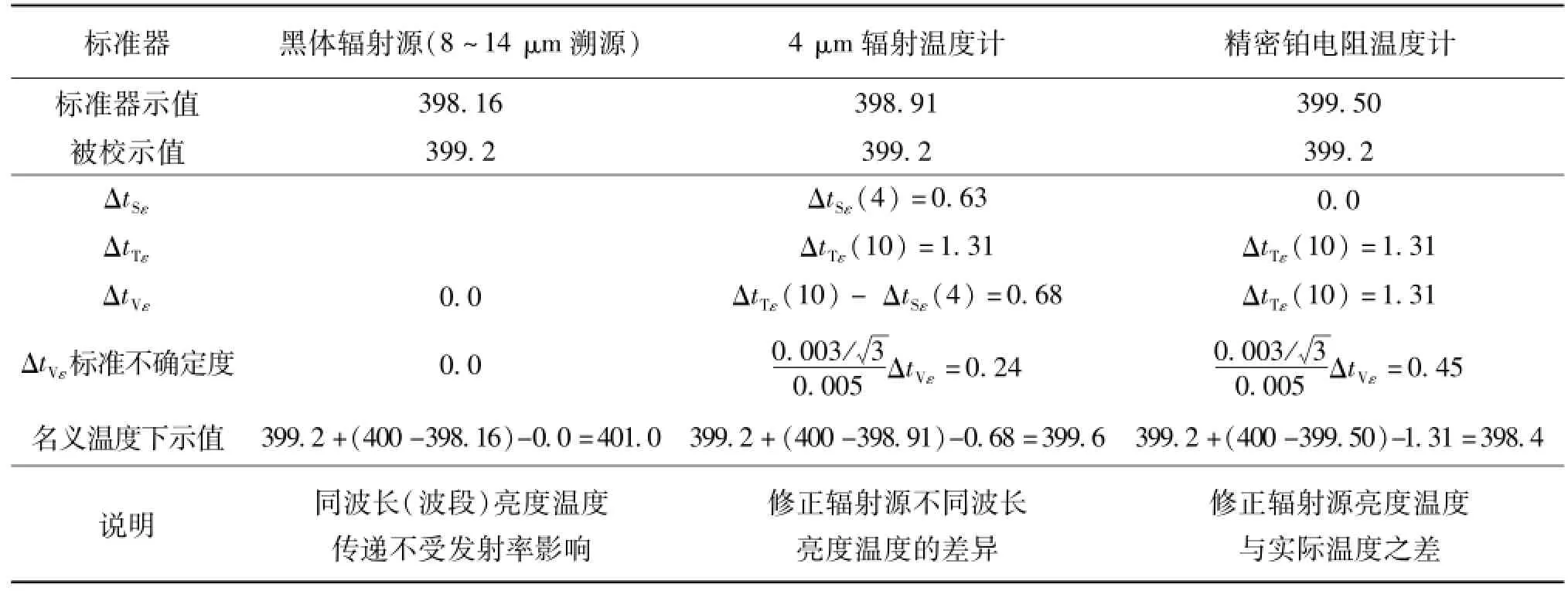
表5 名义温度400℃时辐射温度计校准中的发射率影响修正℃
5 结 论
本文采用有效亮度温度概念,得到由有效亮度温度直接修正到实际温度的公式,讨论的有效亮度温度的发射率修正包含了经典亮度温度的发射率修正和(等温)环境辐射影响修正两方面。有效亮度温度修正模型对于温度范围和测温波长具有广泛适用性,可用于存在环境辐射影响的红外波长测温结果的修正。
对两种近似修正公式的适用性分析表明,对于涉及波长和温度范围较宽的检定与校准,Wien近似和忽略环境辐射近似分别在高温端和低温端存在不适用性,在长波更为突出。广泛采用的经典的高温短波修正模型(采用Wien近似并忽略环境辐射影响,式(5)),对中长波温度计均不适用。式(3)、式(4)具有广泛适用性,其微差形式(式(6))有助于理解发射率影响的物理规律,可用于发射率小幅偏离1的情形。
本文给出辐射温度计检定与校准中不同标准器与不同辐射温度计类型组合时的发射率修正方法。该方法适用于辐射源发射率不确定度对校准结果不确定度传播的计算,也适用于黑体辐射源校准中对标准辐射源的发射率修正和被校辐射源应用中的环境辐射影响修正。
[1] JJG 856—1994 500℃以下工作用辐射温度计[S].
[2] JJG 415—2001 工作用辐射温度计[S].
[3] JJG 67-2003 工作用全辐射温度计[S].
[4] 原遵东.黑体辐射源发射率对辐射测温准确度的影响及修正方法[J].计量学报2007,28(3A):19-22.
[5] Fischer J,Battuello M,Sadli M,et al.Uncertainty Budgets for Realization of ITS—90 by Radiation Thermometry[J].Temperature:Its Measurement and Control in Science and Industry,2003,7:631-638.
[6] Saunders P,Fischer J,Sad liM.Uncertainty Budgets for Calibration of Radiation Thermometers below the Silver Point[J].Int J Thermophys,2008,29(3):1066-1083.
[7] Saunders P.Radiation Thermometry:Fundamentals and Applications in the Petrochemical Industry[M]. Bellingham,Washington:SPIEPress,2007.
[8] 原遵东,王景辉,郝小鹏,等.变温黑体辐射源溯源方式探讨[J].计量学报,2012,33(6A):1~3.
[9] 原遵东.有效亮度温度理论[J].计量学报,2009,30(6):493-497.
[10] Yuan Z D.Effective Radiance Temperature:Concept,Measurement and Effective Wavelength[C]//AIP Conf Proc,Los Angeles,2013.
[11] 原遵东.辐射温度计的等效波长及其应用[J].仪器仪表学报,2009,30(2):374-379.
[12] Sakuma F,Hattori S.Establishing a Practical Temperature Standard by Using a Narrow-band Radiation Thermometer with a Silicon Detector[J].Temperature:ItsMeasurementand Control in Scienceand Industry,1982,5:421/427.
[13] Sakuma F,Kobayashi M.Interpolation equations of scales radiation thermometers[C]//Proceedings of TEMPMEKO’96,6th International Symposium on Temperature and Thermal Measurements in Industry and Science,Torino,1997.
Correcting Effective Radiance Tem perature Measurem ent for Em issivity Effect
YUAN Zun-dong1, XING Bo1, BAICheng-yu1, FU Cheng-yu2, CHEN Gui-sheng3
(1.National Institute of Metrology,Beijing 100029,China;
2.Hubei Institute of Measurement and Testing Technology,Wuhan,Hubei430223,China;
3.National Institute of Measurement&Testing Technology,Chengdu,Sichuan 610021,China)
The classical correction model with the Wien and ambient-radiation-less approximations is not suitable for emissivity correction and uncertainty evaluation middle and low temperature infrared thermometry.The effective radiance temperature concept is adopted to obtain the emissivity effectmodel,with wide validity for measured temperature and measuring wavelength and its differential form with obvious physicalmeanings.The error using the classical correctionmodel is discussed under the midd le and low temperature measurements.The emissivity correction methods are described under different blackbody radiator traceable approaches in radiation thermometer calibration,and an example is given.Themethod discussed is suitable for the em issivity and reflected ambient radiation corrections and associated uncertainties calculations in the applications and calibrations of radiation thermometers and blackbody radiators.
Metrology;Emissivity correction;Effective radiance temperature;Radiation thermometer;Blackbody radiator;Calibration;Uncertainty
TB942
A
1000-1158(2014)06-0578-05
10.3969/j.issn.1000-1158.2014.06.12
2012-09-29;
2014-05-06
原遵东(1960-),福建莆田人,中国计量科学研究院研究员,主要研究方向为温度计量。yuanzd@nim.ac.cn

