基于实测轮廓线的岔道口三维实体建模方法

谭正华,王烈奇,王李管,陈建宏

(1.湘潭大学信息工程学院,湖南湘潭411105; 2.中南大学资源与安全工程学院,长沙410083)

基于实测轮廓线的岔道口三维实体建模方法

谭正华1,王烈奇1,王李管2,陈建宏2

(1.湘潭大学信息工程学院,湖南湘潭411105; 2.中南大学资源与安全工程学院,长沙410083)

在数字矿山系统中,为使错综复杂的地下巷道重建效果能达到矿山的验收标准,根据实测巷道交岔口轮廓线,采用分区(分块)建模思想,提出一种基于实测轮廓线的岔道口三维实体建模方法。将实测的岔道口轮廓数据按其特点分为顶底板和侧面轮廓线点集,采用凸包算法构造顶底板的简单多边形,并对其进行三角化。根据顶底板多边形顶点的先后顺序关系,建立侧面轮廓线的相邻关系,并采用连线框算法对相邻轮廓线进行三角化。实验结果表明,该方法简单有效,可解决任意断面形状、多个岔道口的建模问题,并且已经应用于DIMINE软件的测量插件中,效果良好。

地下巷道;岔道口;实测轮廓线;分区建模;三角剖分;凸包

1 概述

地下巷道岔道口的三维建模是指根据井下开拓、采准等工程验收测量的数据生成三维实体模型的方法,是矿业开发过程中不可缺少的基础技术工作。很多学者在岔道口建模方面做了深入研究。文献[1]仿照了弧段-节点的拓扑结构思想,利用曲线插值对巷道间节点进行处理,但其方法重建的岔道口三维模型会出现扭曲现象。研究者基于断面中线法实现了巷道三维实体建模,但在巷道交岔口的处理上各自存在一定缺点:文献[2]运用三维直线求交,但在岔道口处不能圆滑连接;文献[3]通过加载巷道断面,没有考虑岔道口各巷道宽度变化、巷道截面形状的多样化;文献[4]则运用布尔运算,但在巷道接口处没有进行圆滑处理;文献[5]通过提取CAD平面图的关键点,若岔道的宽度或形状不一样,则在接口处不能圆滑连接。文献[6]将巷道分为结点、节点和巷道中线三类基本元素,在巷道接口处,删除相交产生的公共面,添加相交未闭合的部分,实现了巷道的三维建模,但其处理过程复杂。文献[7]提出了巷道对称建模方法,在交岔口处把三岔口轮廓线分成三个对称多边形,把十字型岔道口轮廓线分为四个对称多边形,用线框建模原理进行重建,但此方法没有考虑巷道交岔口处平滑拼接问题。

地下矿山中存在许多实测的岔道口轮廓数据,形象描述了巷道间的贯通情况,因此基于实测轮廓线的三维建模更接近实际。本文采用分区建模思想,设计一种基于实测巷道交岔口轮廓线,构造顶、底板和腰,生成地下巷道岔道口三维实体模型的方法。

2 算法原理及流程

实测岔道口轮廓线,可以看作是由多个线圈组成,图1所示的三岔口轮廓线则是由S0,S1,S23个线圈组成。图1(a)中点A,B,C为三线圈高程值最大的点,点D,Q,T,P,M,N分别为线圈S0,S1,S2高程值最小的点。图1(b)中S0,S1,S2三线圈高程值最大的点分别为A-B,C-E,F-G之间一系列点。

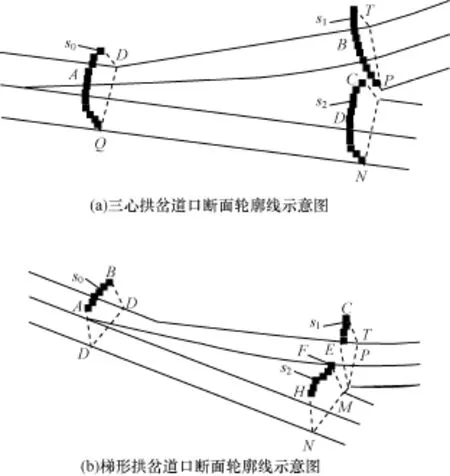
图1 岔道口断面轮廓线示意图

分区建模的思想如下:采用三维空间坐标点来表示线圈上的点,遍历各个线圈找出高程值最小和最大点(集);分别求取顶、底板点集凸多边形,并对顶、底板简单凸多边形进行快速三角化;根据顶(底)板简单多边形顶点之间的先后顺序关系,建立侧面轮廓线的相邻关系;最后采用连线框方法对相邻轮廓线进行建模。建模流程如图2所示。

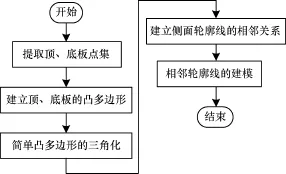
图2 三维岔道口建模流程

3 算法过程

3.1 顶底板数据的提取

点的类C语言定义如下,其中,m_x,m_y,m_z分别表示该点的x,y,z坐标。

遍历各个线圈所有数据,将高程值最小的点集存储到数组m_ptDownArray,将高程值最大的点集存储到数组 m_ptUpArray。每个线圈数据已分成4个部分:底板数据,顶板数据,以及以顶(底)板点为参考点的左边、右边线圈数据。表示如下:

3.2 顶底板凸多边形的建立

平面点集S的凸壳CH(S)是包含S的最小凸集[11]。求取凸壳算法已经相对成熟稳定。文献[8]利用排序算法与简单多边形凸包算法相结合的方法,采用文献[9]算法栈结构处理结构和文献[10]算法思想,简单而快速地求取平面点集的凸包。借鉴文献[8]的方法,快速求取顶、底板平面点集的凸包。由于底板与顶板凸壳求取方法类似,以顶板凸壳的求取方法为例:

步骤1 取出ptUPArray中的点集,将其投影到底板平面。

步骤2 将此点集按最优排序算法排序。

步骤3 顺序连结相邻的顶点,串连形成简单多边形。

步骤4 利用前瞻回溯法搜索简单多边形,得到平面点集的凸包。

步骤5 最后给顶板平面的点赋相应的高程。

生成的顶板凸壳与底板凸壳示意图见图3。

图3 三岔口顶板与底板凸壳

3.3 简单多边形的快速三角化

简单多边形的三角剖分就是在不产生新顶点的条件下将简单多边形分解为一系列不相重叠的三角形[13]。很多学者对简单多边的三角剖分算法有深入的研究[13-16]。其中文献[16]提出的快速三角化算法适合有序的任意简单多边形,时间复杂度为O(n),用此文献的方法,对岔道口轮廓的顶板与底板简单多边形进行三角化,生成结果示意图如图4所示。

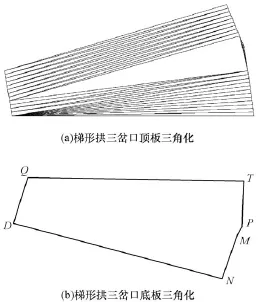
图4 多边形区域三角化示意图

3.4 相邻轮廓线关系的确立与建模

3.4.1 轮廓线相邻关系的确定

在求取顶、底板凸多边形的过程中已经对顶、底板上的点集进行了排序,因而可以把顶(底)板凸多边形上的顶点序列视为线圈序列。

三岔口俯视图如图5所示。假设线圈顺序与图中线圈S0,S1,S2顺序一致。对于实测轮廓线圈数据,利用已经提取出来了的底板数据与顶板数据,根据线圈上各点的x值或y值的差异生成以顶板顶点为参照点的左边、右边轮廓数据。

三心拱俯视图如图5(a)所示,线圈S0中A-Q所代表的轮廓数据与线圈S1中的B-T所代表的轮廓数据相邻,按顺时针方向遍历一周,所有线圈的相邻关系都已确定。梯形拱侧面轮廓数据示意图如图5(b)所示,线圈S0中B-Q所代表的轮廓数据与线圈S1中的C-T所代表的轮廓数据相邻,按顺时针方向遍历一周,可知,线圈S1中E-P所代表的轮廓数据与线圈S2中的F-M所代表的轮廓数据相邻,线圈S2中G-N所代表的轮廓数据与线圈S0中的A-D所代表的轮廓数据相邻。

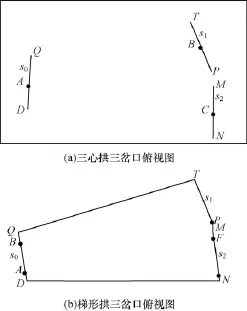
图5 三岔口俯视图

3.4.2 相邻轮廓线的建模

在生成了底板与顶板三角化网格之后,基于实测轮廓线的岔道口建模问题转化为基于底板与顶板轮廓线重建其相邻轮廓线表面的问题。基于物体表面轮廓线[17-19]的三维重建方法已经很成熟。根据相邻截面轮廓曲线一般具有相似这一性质,文献[18]首先对轮廓曲线上的点进行预处理后,采用角点测法与多边形法结合的方法来计算控制点,再对其进行分块,然后在分块后的小曲线段上进行三角划分,实现了一种对物体表面进行三角划分的方法。由于此方法没有考虑控制点一对多的情况,文献[19]对文献[18]的方法进行了改进:(1)采用一种改进的CSS方法对轮廓曲线角点进行提取。(2)采用了一种新的配对方法对角点进行配对,根据曲线间距离设定动态阈值。(3)轮廓相似性判断。(4)在相似轮廓线之间根据配对的情况来分块。在分块后的小曲线段上进行简单三角划分与文献[17]所用的方法一样。采用文献[19]中的方法对左右轮廓线进行连线框操作,生成了三维岔道口实体表面模型。基于分层轮廓线的网格三角化如图6所示。

图6 基于分层轮廓线的网格三角化

4 算法分析和应用

4.1 算法时间复杂度分析

该算法的时间复杂度分析如下:

(1)凸壳的形成,设顶板的顶点数目为k,排序算法的最坏时间复杂度为O(klog(k)),将点集按顺序连接成简单多边形的时间复杂度为O(k),求取简单多边形凸包的时间复杂度为O(k),因此,顶板建模的复杂度为O(klog(k)),同理,设底板的顶点数目为m,则底板建模复杂度为O(mlog(m))。

(2)简单多边形的三角化,顶、底板凸多边形的顶点数分别为k、m,三角化的时间复杂度为O(k)+O(m)。

(3)提取顶底板数据、连线框算法,时间复杂度与顶点数目都接近线性,故总的时间复杂度为:O(klog(k))+O(mlog(m))。

4.2 应用实例

在Windows XP操作系统上,通过VC++开发工具和 HOOPS可视化工具包实现了该算法。“DIMINE”数字矿山软件系统是中南大学数字矿山研究中心研发的一套集矿床地质建模、矿山工程测量和地下、露天矿床开采设等于一体的智能化、可视化软件系统。该系统的矿山工程测量和出图模型采用了该算法。此算法应用于某矿山巷道建模实例如图7所示,其局部精细图如图7(b)(图7(a)中①)、图7(c)(图7(a)中②)所示。

另外,当线圈顶点的数目为任意多个,此算法能稳定地重建出三维岔道口实体模型;当线圈形状为三角形、圆和不规则多边形等极致情况,算法也能稳定的重建出三维岔道口实体模型;当线圈数目为任意多个,算法依然能稳定的重建出三维岔道口实体模型。

图7 巷道渲染图

5 结束语

本文提出一种实测地下巷道岔道口三维建模方法。该方法采用分区建模思想,将实测岔道口轮廓数据按其特点进行分类,采用凸包算法、连线框算法和网格三角化算法,建立了虚拟系统中的三维岔道口实体,解决了数字矿山三维实测巷道重建的难点问题,该方法具有以下优点:(1)能有效地解决任意断面形状的岔道口建模问题。(2)能有效解决由任意多个巷道组成的岔道口建模问题。(3)适用于包含2个线圈的单体实测巷道建模问题。

［1］ 魏占营,王宝山,李青元.地下巷道的三维建模及C++实现［J］.武汉大学学报,2005,30(7):650-653.

［2］ 汪云甲,伏永明.矿井巷道三维自动建模方法研究［J］.武汉大学学报,2006,31(12):1097-1099.

［3］ 葛永慧,王建民.矿井三维巷道建模方法的研究［J］.工程勘察,2006,(10):46-49.

［4］ 徐志强,杨邦荣,王李管,等.巷道实体的三维建模研究与实现［J］.计算机工程与应用,2008,44(6):202-205.

［5］ 万 金,张 凯,陈建勋.一种三维地下巷道建模的改进方法［J］.工业控制计算机,2012,25(8):85-87.

［6］ 谢义林,汪云甲.姚连璧.巷道三维构模及虚拟交互研究［J］.计算机工程与应用,2009,45(23):231-235.

［7］ 张志华,侯恩科,赵 洲,等.一种新的3D巷道建模方法——对称建模法［J］.金属矿山,2009,39(5):107-111.

［8］ 金文华,何 涛,刘晓平,等.基于有序简单多边形的平面点集凸包快速求取算法［J］.计算机学报,1998, 21(6):533-539.

［9］ Chen Chern-Lin.Computing the Convex Hull of a Simple Polygon［J］.Pattern Recognition,1989,22(5):561-565.

［10］ Sklansky J.Measuring Concavity on Rectangular Mosaic［J］.IEEE Transactions on Computers,1972,21(12): 1355-1364.

［11］ 周培德.计算几何—算法分析与设计［M］.北京:清华大学出版社,2000.

［12］ 程三友,李英杰.一种新的最小凸包算法及其应用［J］.地理与地理信息科学,2009,25(5):43-45.

［13］ 马小虎,潘志庚,石教英.基于凹凸顶点判定的简单多边形Delaunay三角剖分［J］.计算机辅助设计与图形学学报,1999,11(1):101-104.

［14］ Gareym R,Johnsond S,Preparata F P.Triangulating a Simple Polygon［J］.Information Proceeding Letters, 1978,7(4):175-179.

［15］ Seidel R.A Simple and fast Incremental Randomized Algorithm Forcomputing Trapezoidal Decompositions and for Triangulating Polygons［J］.Comput Geom Theory Appl,1991,1(1):51-64.

［16］ 毕 林,王李管,陈建宏,等.快速多边形区域三角化算法与实现［J］.计算机应用研究,2008,25(10):3030-3033.

［17］ Keppel E.Approximating Complex Surface Interpolation Technique for Reconstruction 3D Objects from Serial Cross-sections［J］.Graphical Models and Image Processing,1989,48(1):124-143.

［18］ 周 焰,李德华,陈振羽,等.三维物体表面三角划分的快速算法［J］.中国图像图形学报,2000,5(9):764-768.

［19］ 周 焰,李德荣,徐长勇.一种基于区域分割的三角划分方法［J］.武汉大学学报:信息科学版,2003,28(2): 227-230.

编辑 索书志

3D Modeling Method for Fork Based on Measured Contour

TAN Zhenghua1,WANG Lieqi1,WANG Liguan2,CHEN Jianhong2
(1.College of Information Engineering,Xiangtan University,Xiangtan 411105,China;
2.School of Resources and Safety Engineering,Central South University,Changsha 410083,China)

In the digital mine system,in order to make intricate underground roadway reconstruction effect reach the acceptance criteria of the mine,a 3D modeling method for fork entity based on measured contour using a partition or block modeling idea is proposed,which is is based on the measured contour of the roadway cross fork.The measured contour data of fork is classified by features into top,bottom and side contour point set.The convex hull algorithm is used to construct the roof and floor of a simple polygon,and triangulation.Based on the order of the top(bottom)plate polygon vertices,the adjacent relationship of the lateral broadside contours is established,and connection box algorithm is used to triangulate for adjacent contours.Experimental results show that,the algorithm is simple and effective and can solve any cross-sectional shape and any multiple fork modeling problems.The algorithm has been applied to the measurement plug-in contained in DIMINE software,and has good results.

underground laneway;fork;measured contour;partition modeling;triangulation;convex hull

1000-3428(2014)11-0233-04

A

TP391.41

10.3969/j.issn.1000-3428.2014.11.046

国家自然科学基金资助项目(51374242);湖南省自然科学基金资助项目(14JJ3077);湖南省教育厅基金资助一般项目(13C917);湘潭大学科研启动费基金资助项目(11QDZ11)。

谭正华(1981-),男,讲师、博士,主研方向:计算机辅助设计,数字矿山理论与技术;王烈奇,硕士研究生、CCF会员;王李管、陈建宏,教授、博士生导师。

2013-11-06

2013-12-31E-mail:wanlieqi@163.com

中文引用格式:谭正华,王烈奇,王李管,等.基于实测轮廓线的岔道口三维实体建模方法[J].计算机工程,2014, 40(11):233-236.

英文引用格式:Tan Zhenghua,Wang Lieqi,Wang Liguan,et al.3D Modeling Method for Fork Based on Measured Contour[J].Computer Engineering,2014,40(11):233-236.