基于阈值分割与多边形扫描求交的明暗恢复形状重构模型冗余信息去除

吴凤和， 王金芬， 王 军， 王 鑫

（燕山大学机械工程学院，河北秦皇岛 066004）

基于阈值分割与多边形扫描求交的明暗恢复形状重构模型冗余信息去除

吴凤和， 王金芬， 王 军， 王 鑫

（燕山大学机械工程学院，河北秦皇岛 066004）

针对明暗恢复形状重构模型存在图像背景信息问题，提出基于阈值分割与多边形扫描求交的冗余信息去除方法。通过阈值分割将图像转换为二值图像，采用形态学方法修补二值图像中的缺陷，并利用微分算子提取图像的二维轮廓；通过多边形扫描求交将图像分割为目标区域和背景区域；根据由阴影恢复形状原理重构三维模型，并通过二维轮廓与三维形貌的信息匹配去除图像背景冗余信息。实例表明，该方法能够有效去除明暗恢复形状重构模型中的图像背景冗余信息，保证重构模型的形状精度。

计量学；背景去除；多边形求交；轮廓提取；形态学

1 引 言

作为计算机视觉中三维数据被动获取的重要手段，由明暗恢复形状（Shape from Shading，简称SFS）方法只需物体的单幅图像就能恢复物体表面的三维形貌，与其它基于图像信息的三维重建方法相比，具有操作简单、成本低、效率高等特点。SFS是由Horn［1］于1970年提出的，其基本原理是利用单幅图像中物体表面的明暗变化恢复物体表面各点的相对高度或表面法方向等参数值，从而得到反映物体三维形貌的模型。近年来，国内外的许多学者对其进行了研究［2～4］，并将其应用在检测与测量、医学图像处理、自然景物模拟、模式识别等领域［5～8］。

SFS方法借助图像中各像素点的灰度信息重构物体表面的三维模型，即图像像素点与SFS重构模型中的数据点间存在一一对应关系。由于任何图像都包含背景，因此，SFS重构模型中既包含图像中物体的信息也包括图像中背景的信息。对于逆向工程等应用来说，其目的是得到图像中物体的三维模型，而不应包含图像中的背景信息，因此，开展SFS重构模型的背景冗余信息去除研究有重要的理论意义和实用价值。本文综合运用阈值分割［9，10］、形态学修补［11］及多边形扫描求交等方法，提出一种实用的SFS重构模型冗余信息去除方法。首先，通过阈值分割将图像转换为二值图像，利用数学形态学方法修补二值图像中的缺陷，并通过微分算子进行边缘检测，从而得到图像中目标的二维轮廓；再将二维轮廓看做多边形，通过多边形扫描求交将图像分割为目标区域和背景区域；最后，通过SFS方法进行三维重构，并根据三维形貌数据点与二维图像像素点间的一一对应关系去除三维模型中的图像背景信息，得到物体的数字化模型。

1 三维形貌恢复

SFS过程是成像的逆过程，即根据二维图像恢复物体的三维形貌。为简化问题，传统的SFS模型做了3个假设：①光源为无限远处点光源；②反射模型为朗伯体表面反射模型；③成像几何关系为正交投影。在此基础上，根据光度学原理得到如下反射方程：

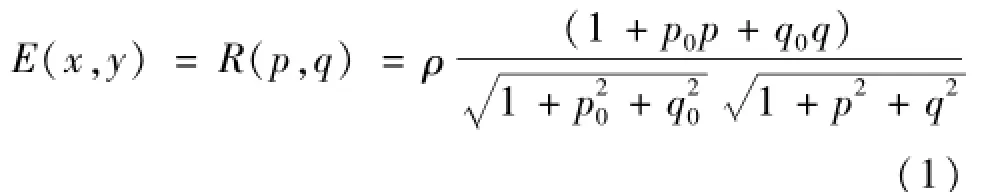
式中：E（x，y）为图像灰度；R（p，q）为反射函数；ρ为图像亮度，（p0，q0，－1）为光源入射方向；（p，q，－1）为物体表面法线方向。

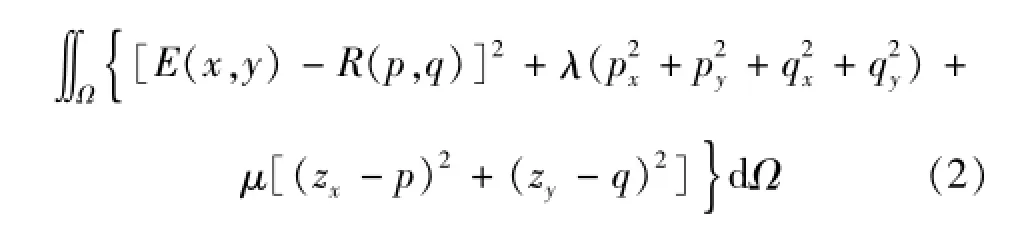
为解决式（1）的病态特性，分别引入光滑性约束、亮度约束和梯度一致性约束，构造全局性最优化函数：式中：第1项为亮度误差，第2项为光滑性误差，第3项为梯度一致性误差；λ和μ分别为表面光滑性误差和梯度一致性误差的加权因子；（x，y）为离散化的像素坐标。

对式（2）求变分后得到优化函数极值存在的必要条件

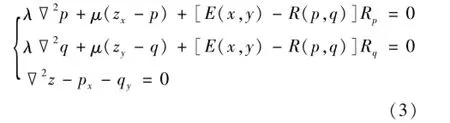
式中：∇2为拉普拉斯算子，Rp，Rq分别为函数R关于p和q的偏导数。

应用交错网格方法将p，q，z，px，qy，zx，zy及∇2算子离散化，再通过Gauss-Seidel迭代法，求解得到物体表面梯度p，q和表面高度z的网格值，从而实现包含图像背景信息的三维重构。

2 图像轮廓提取

2.1 阈值分割

由于常用的边缘检测算子［12，13］得到的边缘通常无法保证单像素宽，往往出现孤立或者分段连续的边缘，因而需要细化、连接等后处理，处理过程较复杂。因此，选择基于区域的阈值法进行图像分割。在逆向工程领域中，图像通常只包含工件和背景两类区域，因此采用单阈值法。其原理如下。

设图像的灰度区间为［Zmin，Zmax］，选取阈值Zt，且Zmin＜Zt＜Zmax，令图像中灰度大于或等于Zt的像素的灰度值为1，小于Zt的像素的灰度值为0，则输出的二值图像为：

2.2 形态学修补

由阈值分割得到的边缘存在断线、凹洞等缺陷，使提取的轮廓包含多个闭合的小区域。为了简化轮廓，便于处理，采用形态学法对二值图像进行缺陷修补。其原理是：利用结构元素对图像进行膨胀、腐蚀、开启、闭合等形态学变换，通过选取合适的结构元素和运算形式使图像在一定方向上增厚或减薄，从而达到修补缺陷、去除噪声的目的。为达到这一目的，形态学运算形式的选择必须遵循以下原则：

（1）在保持图像基本形状特征的基础上，平滑边界，消除图像中的细小孔洞和毛刺等缺陷；

（2）为保证轮廓提取精度，应保持图像中目标的尺寸及形状基本不变。

由形态学各种运算的定义及性质可知，只有开运算和闭运算在修补缺陷的同时能够保证不产生全局的几何失真。因此，只能采用开运算和闭运算的组合形式进行形态学缺陷修补处理。

2.3 轮廓提取

由于二值图像只有黑、白2种灰度值，本文采用Robert微分算子法［14］进行边界点判断及轮廓提取。Robert算子采用对角线方向相邻像素之差近似梯度来进行边缘点的判断，对数字图像f（x，y）每一像素点，取其梯度值：

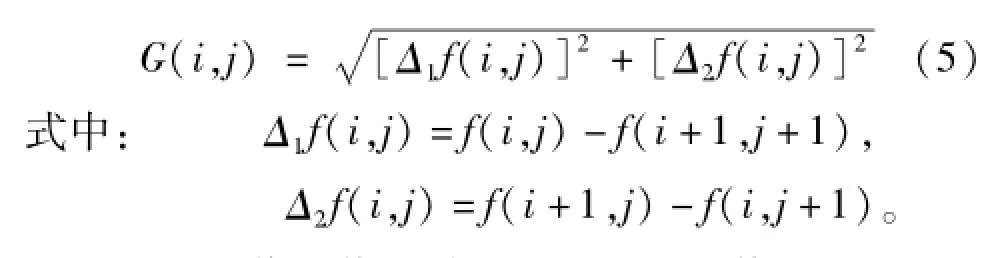
由于二值图像的特殊性，选取阈值G0（i，j）＝0，当G（i，j）＞G0（i，j）＝0时，该像素点为边界点，取灰度值为1；否则为背景或目标内部点，取灰度值为0。

3 多边形区域分割

经过轮廓提取处理后就得到了连续的二维轮廓。由于任意复杂的二维轮廓均可看做多边形，因此利用多边形扫描求交方法进行区域分割，其技术路线如图1所示。

3.1 多边形扫描求交

多边形扫描求交是指通过扫描线与二维轮廓线求交，得到每行中的边界点。如图2所示的扫描线①与多边形P01P02P03P04P05P06P07交于E、F、G、H四点，则E、F、G、H四个交点即为边界点。

得到边界点之后，需根据边界点的性质，决定边界点的取舍。交点取舍应遵循如下步骤：

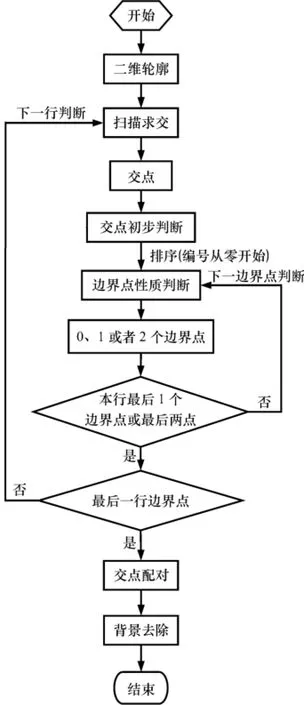
图1 多边形扫描求交

步骤1：交点的初步判断：

首先保留多边形求交中得到的孤立的边界点和边界点中小线段的端点。如图2所示，扫描线②与多边形P01P02P03P04P05P06P07相交于A、B、C、D四点的同时，还相交于BC线段，这时只保留A、B、C、D四点。

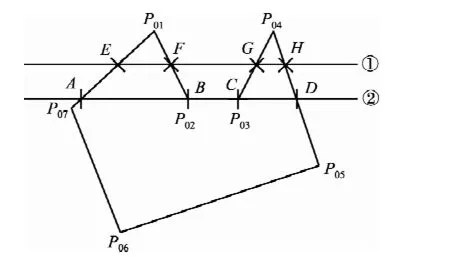
图2 交点的初步判断

步骤2：边界点性质的判断：

边界点可分为局部最高点、局部最低点、小线段的端点等，在交点性质判断的过程中，首先对每行中经初步判断得到的边界点进行排序，并按照从左到右的顺序依次进行判断。

（1）局部最高点

对于本行中的一点，若上一行经步骤1保留下来的边界点的纵坐标与该点的纵坐标之差的绝对值小于等于1的边界点个数为0，下一行经步骤1保留下来的边界点的纵坐标与该点的纵坐标之差的绝对值小于等于1的边界点个数大于等于2，并且此点为非小线段端点，则该点为局部最高点，算作0个边界点，并去掉。如图3所示，扫面线⑥与多边形P01P02P03P04P05P06P07P08P09P10P11P12P13P14P15P16P17P18P19交于0、1、2、3、4、5、6七点，其中1点为局部最高点，算作0个边界点。

图3 交点性质判断

（2）局部最低点

对于本行中的一点，若上一行经步骤1保留下来的边界点的纵坐标与该点的纵坐标之差的绝对值小于等于1的边界点个数为2，下一行经步骤1保留下来的边界点的纵坐标与该点的纵坐标之差的绝对值小于等于1的边界点个数为0，且该点为非小线段端点，则该点为局部最低点，算作2个边界点。如图3所示，扫描线④与多边形交于0、1、2三点，其中1为局部最低点，算作2个边界点。

（3）小线段的端点

首先做如下定义：

①若小线段的左端点的纵坐标与上一行（或下一行）中经步骤1保留下来的边界点的纵坐标之差的绝对值小于等于1的边界点个数为非0，且小线段的右端点的纵坐标与下一行（或上一行）中经步骤1保留下来的边界点的纵坐标之差的绝对值小于等于1的边界点个数为非0，则定义a＝1；

②若小线段的左、右端点的纵坐标与上一行（或下一行）中经步骤1保留下来的边界点的纵坐标之差的绝对值小于等于1的边界点个数均非0，则定义a＝2；

边界点的个数根据上述定义和如下规则确定：

①若小线段的左端点的序号为奇数，且a＝1，则左端点算作2个边界点，右端点算作1个边界点。如图3所示，扫描线①与多边形交于0、1、2三点，小线段左端点算作2个边界点，右端点算作1个边界点；

②若小线段的右端点的序号为奇数，且a＝1，则右端点算作2个边界点，左端点算作1个边界点。如图3所示，扫描线②与多边形相交于0、1、2三点，则小线段左端点算作1个边界点，右端点算作2个边界点；

③若小线段的左端点的序号为奇数，且a＝2，则去除左、右端点，均算作0个边界点。如图3所示，扫描线③与多边形交于0、1、2、3、4、5六点，其中小线段的左右端点3、4均算作0个端点，扫描线⑤与多边形交于0、1、2、3四点，其中小线段的左右端点1、2均算作0个端点；

④其余情况，左、右端点均算作一个端点。如图3所示，扫描线⑦与多边形交于0、1、2、3四个端点，小线段左右端点均算作1个边界点。

3.2 冗余信息去除

通过以上多边形扫描求交算法得到了每行中的边界点，为了防止边界区域的扩大，需保留左边界点，而去除右边界点。因此冗余信息去除的步骤如下：

（1）交点配对：将多边形扫描求交算法保留下来的交点按照第一个与第二个，第三与第四个……依次类推的规则进行配对，两两成对。

（2）背景去除：根据二维图像像素点与SFS恢复的三维形貌数据点间的一一对应关系，借助多边形扫描求交及交点配对结果去除SFS重构模型中的图像背景冗余信息。去除原则是：只保留SFS重构模型中交点配对区间之内的信息，去除配对区间之外的冗余信息。

4 实 例

为验证图像背景冗余信息去除的效果，以骆驼图像为例进行试验，结果如图4所示。图4（a）为输入的原始图像；图4（b）为图4（a）经SFS方法得到的三维形貌；图4（c）为图4（a）经阈值分割得到的二值图像，由图可看出经阈值分割得到的二值图像边缘存在断线、凹洞等缺陷；图4（d）为对图4（c）经过形态学修补之后的二值图像，消除了图4（c）中二值图像边缘的断线、凹洞等缺陷；图4（e）为图4（d）经轮廓提取后得到的连续的二维轮廓；图4（f）为由图4（b）和图4（e）经信息融合，去除配对区间之外的冗余信息得到的数字化模型。由图可知，图像的背景去除效果较好，保留了图像中物体边缘的细节信息。

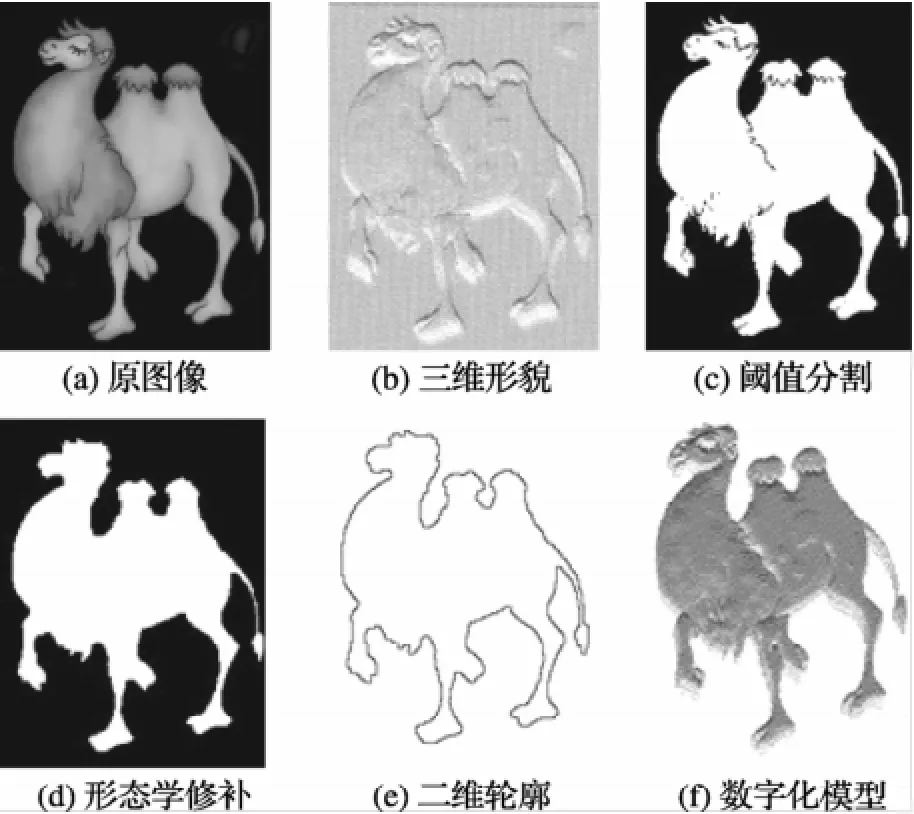
图4 背景去除

5 结 论

针对SFS重构模型存在图像背景冗余信息问题，本文提出基于阈值分割与多边形扫描求交的冗余信息去除方法。将阈值分割、形态学修补及多边形扫描求交等方法相结合，精确获取二维轮廓边界点信息，并通过二维轮廓与三维形貌的信息匹配去除重构模型中的图像背景信息。由实验结果可以看出，该方法能有效去除SFS重构模型中的图像背景冗余信息，保证重构模型的形状精度，对拓展SFS方法的应用领域具有重要意义。

［1］ Horn B K P.Shape from Shading：method for obtaining the shape of a smooth opaque object from one view［R］. MIT ProjectMAC TR-79，1970.

［2］ Hisashi S.A Shape-from-Shading Method of Polyhedral Objects Using Prior Information［J］.IEEETransactions onPatternAnalysisandMachineIntelligence，2006，28（4）：612－624.

［3］ Takayuki O，Koichiro D.Shape Reconstruction from an Endoscope Image by Shape from Shading Technique for a Point Light Source at the Projection Center［J］.Computer VisionandImageUnderstanding，1997，66（2）：119－131.

［4］ Dimitris S，Dim itris M.Incorporating Illum ination Constraints in Deformable Models for Shape from Shading and Light Direction Estimation［J］.IEEETransactionson PatternAnalysisandMachineIntelligence，2003，25（2）：247－264.

［5］ Wu Fenghe，Sun Lei.Single image based reverse engineering method［J］.JournalofComputational InformationSystems，2009，5（1）：193－199.

［6］ 王国珲，韩九强，张新曼，等.一种新的基于从明暗恢复形状的月球表面三维形状恢复算法［J］.宇航学报，2009，30（6）：2265－2269.

［7］ 宋丽梅，周兴林，徐可欣，等.基于单幅测量图像的三维缺陷检测技术［J］.光学学报，2005，25（9）：1195－1200.

［8］ 严涛，陈彦云，吴恩华.一种基于单幅图像的树木深度估计与造型方法［J］.计算机学报，2000，23（4）：386－392.

［9］ 吴凤和，张晓峰，施法中.基于单幅图像数据的三维重构方法研究.中国机械工程，2007，18（17）：2071－2075.

［10］ 程琦，赵军，刘宇.指针式仪表示值识别系统研究［J］.计量学报，2009，30（5A）：192－195.

［11］ 吴凤和.基于计算机视觉测量技术的图像轮廓提取方法研究［J］.计量学报，2007，18（1）：18－22.

［12］ 吕哲，王福利，常玉清，等.机器视觉测量中一种新的边缘检测算法［J］.计量学报，2009，30（3）：193－196.

［13］ 张洪涛，段发阶，丁克勤，等.带钢表面缺陷视觉检测系统关键技术研究［J］.计量学报，2007，28（3）：216－219.

［14］ 章毓晋.图象理解与计算机视觉［M］.北京：清华大学出版社，2000.

Redundant Information Removing of SFS Reconstructed Model Based on Threshold Segmentation and Polygons Intersecting

WU Feng-he， WANG Jin-fen， WANG Jun， WANG Xin
（College of Mechanical Engineering，Yanshan University，Qinhuangdao，Hebei066004，China）

To remove the redundant points of shape from shading reconstructed model，a practical methods based on threshold segmentation and polygons intersecting is proposed.The image is converted into binary image through threshold segmentation technique，the defects contained in image are remedied by morphological method，and the 2D contour is extracted by using the differential operator，the binary image is divided intoobjective region and background region by using the polygons intersectingmethod；the 3D model is reconstructed by using shape from shading method，and the redundant points of shape from shading reconstructed model are removed through fusing the information of 3D profile and 2D contour.Experiment results showed that themethod proposed can effectively remove redundant points of shape from shading reconstructed model，and it is helpful for improving the shape precision of shape from shading reconstructed model.

Metrology；Background removing；Polygons intersecting；Contour extraction；Morphology

TB96

A

1000-1158（2014）01-0044-05

10．3969／j．issn．1000-1158．2014．01．10

2012-10-08；

2013-03-06

国家科技重大专项（2011ZX04002-111）；河北省自然科学基金（E2011203091）；教育部博士学科点专项基金（20121333110011）作者简介：吴凤和（1968－），男，内蒙古扎兰屯人，燕山大学教授，博士生导师，主要研究方向为数字化测量与建模、数字化制造。risingwu＠ysu.edu.cn