骨折创伤断面微型二维力传感器研制

朱坚民， 黄之文， 李海伟， 翟东婷， 王 军

（上海理工大学机械工程学院，上海 200093）

骨折创伤断面微型二维力传感器研制

朱坚民， 黄之文， 李海伟， 翟东婷， 王 军

（上海理工大学机械工程学院，上海 200093）

针对骨折创伤断面轴向压力和径向剪切力的实时精确测量要求，设计了基于E型圆膜片式结构弹性体的微型二维力传感器，建立了传感器弹性体应变的理论分析模型。根据理论分析模型对传感器弹性体的主要结构尺寸进行了优化，设计了弹性体上应变片的贴片位置和组桥方式。对传感器进行了标定实验，获得了标定数据。标定实验结果表明：传感器灵敏度为2.9MPa／N，轴向力满量程非线性误差为1.1783%，径向力满量程非线性误差为1.0416%。

计量学；二维力传感器；骨折创伤；应变分析；弹性体；标定

1 引 言

给予骨折创伤断面合理的刺激力可以促进骨骼的生长，提高骨折愈合的速度及质量［1］。目前应用于骨折临床治疗的各种类型的固定器都可对骨折端施加刺激力，但对于施加于骨折创伤断面的力的大小和方向均无法获知，依赖于手术医生的感觉。另外，由于固定器本身所存在的加工误差和安装误差，骨折愈合过程中的创伤断面处于由轴向压力和径向剪切力构成的二向应力状态。适宜的轴向压力能促进骨骼的生长，而径向剪切力会破坏骨桥的搭接，延迟骨折愈合时间，甚至会引起骨折治疗的失败［2］。在骨骼力传感器的研究方面，文献［3］采用空心圆柱形航空铝外表面贴应变片封装成传感器实现了对干骨轴向力的测量，文献［4］采用S型应变式力传感器，实现了对活体山羊股骨轴向力的测量，文献［5］采用两根对称布置的辐条作为力敏元件，设计了一种用于骨外固定器的横向力测量传感器，上述传感器只能实现单维力测量。在多维力传感器的研究方面，文献［6～18］采用悬臂梁、薄壁圆筒形、双E膜片、十字梁等多种弹性体结构设计了一系列多维力传感器，但这些力传感器很难用于创伤断面二维力的测量，主要原因有：（1）传感器的体积较大，无法串接于骨外固定器的施力杆中；（2）传感器无测力保护装置，难以适应临床骨折治疗的特殊要求；（3）传感器的重量较大，不便于骨折治疗病人的活动；（4）传感器大多能实现创伤断面轴向压力的测量，但无法同时对创伤断面径向剪切力进行检测。

为了保证骨折愈合的速度及质量，必须对骨折愈合过程中创伤断面的二维应力状态进行实时测量与控制。本文基于E型圆膜片式结构弹性体，设计了串接于骨外固定器施力杆中的微型二维力传感器。

2 传感器弹性体的结构设计

设计的二维力传感器由弹性体和刚性底座组成，结构如图1所示。骨折愈合过程较长，愈合初期骨折创伤断面上的轴向压力大约为70 N，而在愈合的后期，轴向压力接近1 N。创伤断面上的径向剪切力主要由固定器的安装误差引起，径向剪切力相对于轴向压力要小的多，一般在5 N以下。因此，所设计的二维力传感器应具有测量范围大、灵敏度高的特点。本文采用一个弹性体实现对轴向压力和径向剪切力的同时测量。弹性体采用E型圆膜片结构作为弹性敏感元件，其结构如图2所示。弹性体中间凸起的部分是硬中心，与骨外固定器的加力杆相连接，直接承受作用力F。力F可以分解为垂直于硬中心表面的轴向压力F1和平行于硬中心表面的径向剪切力F2，通过在弹性体的相应位置粘贴应变片，即可实现对创伤骨骼轴向压力F1和径向剪切力F2的测量。弹性体的主要结构尺寸有内径a、外径b、膜厚h及硬中心高度l。

图1 骨折创伤断面微型二维力传感器的结构图

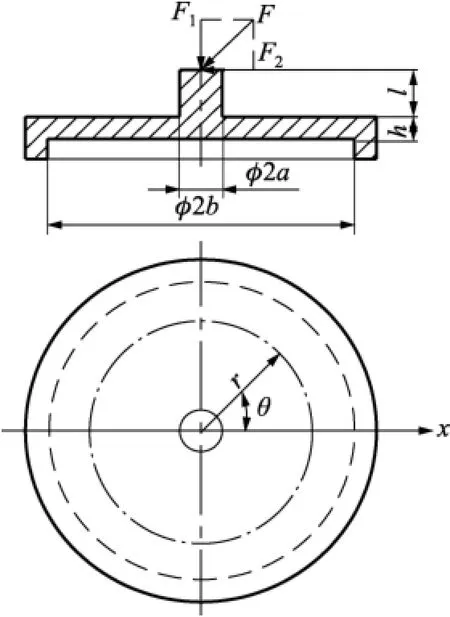
图2 E型圆膜片式弹性体

3 传感器弹性体的应变分析

弹性体的设计是二维力传感器设计的关键，分析弹性体受力后的应变特性，对于确定弹性体结构尺寸、应变片贴片和组桥方式极其重要。考虑到弹性体结构的对称性，其受力变形依据圆薄板小挠度变形处理。下面分别求解弹性体在轴向压力F1和径向剪切力F2作用下的应变分析。因弹性体具有x方向结构的对称性，极坐标r轴取x轴正向，极坐标θ角表示和径向剪切力F2作用方向的偏转角度。

3.1 轴向力F1作用下的弹性体应变分析

如图2，在轴向力F1的作用下，弹性体边界条件可以等效为外圆周固定，集中力作用在硬中心的圆形薄板。根据板的小挠度变形理论和虚功原理可求得弹性体上任意一点的法向位移w（r）为：

由式（2）、式（3）可以看出：在传感器结构尺寸和材料确定的情况下，εr1、εθ1和F1成正比。只要通过应变片测得弹性体上的径向应变εr1或切向应变εθ1，即可以实现对轴向力F1的测量。

3.2 径向剪切力F2作用下的弹性体应变分析

如图3，在径向剪切力F2作用下，F2作用于硬中心可等效为集中力偶矩M作用于弹性体中心。设q0为弹性体膜片内受到的横向载荷，令膜片挠曲面为w（r，θ），其反对称变形如式（4）所示。

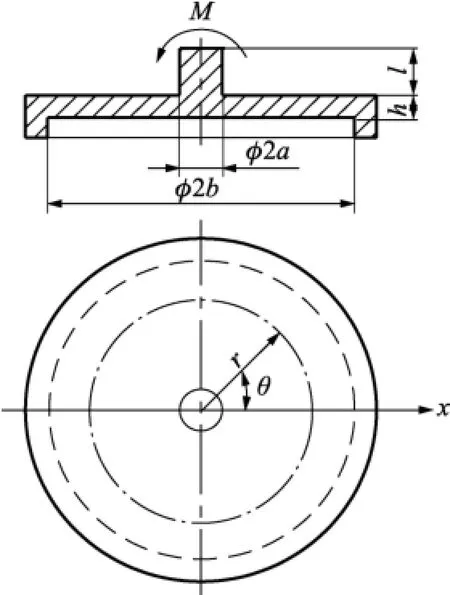
图3 径向剪切力F2等效模型

由式（7）、式（8）所示的弹性体应变的解析解可知：当传感器的结构尺寸和材料确定的情况下，弹性体所产生的应变εr2、εθ2和径向剪切力F2成比例关系。只要通过应变片测得弹性体上的径向应变εr2或切向应变εθ2，即可实现对径向剪切力F2的测量。

4 传感器弹性体的结构尺寸优化

传感器设计过程中，弹性体材料的选择十分重要。一方面，材料的后效、蠕变、品质因数直接影响传感器的迟滞、重复性、满量程漂移；另一方面，作为弹性体的材料必须易机械加工、研磨和抛光。本文采用40CrNiMo作为弹性体的材料，其屈服极限高，弹性模量的温度系数小，线膨胀系数小，弹性模量接近于常数，材料的弹性滞后小，加工方便，加工后的残余应力小。这些特性能满足创伤断面应力测控环境的要求。40CrNiMo的机械性能如表1所示。

表1 40CrNiMo的机械性能表

由图2和图3，传感器弹性体的主要结构尺寸包括膜片内外半径a和b，膜厚h和硬中心高度l。其中，硬中心高度l对传感器性能的影响不大，考虑到力杆螺纹连接的长度，确定为l＝4 mm。膜厚h影响传感器的测量范围，厚度h越大，传感器的测量范围越大，但灵敏度会降低。膜厚h过小，则传感器的强度和刚度不足，有可能会产生不可恢复的形变。内外圆半径比a／b则影响传感器的线性度和灵敏度，a／b越大，传感器的灵敏度越低，同时线性度也会降低。本文以内外圆半径比a／b和膜厚h为优化参数，以传感器的灵敏度和线性度为优化目标，对传感器的主要结构参数进行优化。

4.1 内外圆半径比a／b的优化

当轴向力F1单独作用时，由公式（2），可认为F1、μ、E、h为定值，这种假定不会影响应变的变化趋势。根据弹性体变形的小挠度理论，内外半径比a／b需满足1／80≤h／（b－a）≤1／8，a≤r≤b，r为膜片上任意点至膜片中心的距离。考虑到传感器硬中心会受到径向剪切力作用，a不能过小，否则在传感器测量范围内将会使硬中心产生无法恢复的变形或断裂，经计算需保证a／b≥0.2。基于以上要求，确定内外半径比a／b的变化范围为0.2≤a／b≤0.9。由式（2）可计算在轴向力F1单独作用时径向应变εr1与r之间的关系曲线，如图4所示。

图4F1单独作用时εr1与r／b的关系

在径向剪切力F2单独作用时，由式（7），可认为D、E、C为定值，这种假定不会影响应变的变化趋势。同样，a／b变化范围为0.2≤a／b≤0.9，取θ＝0°，由公式（7）可计算出在径向剪切力F2单独作用时径向应变εr2与r之间的关系曲线，如图5所示。

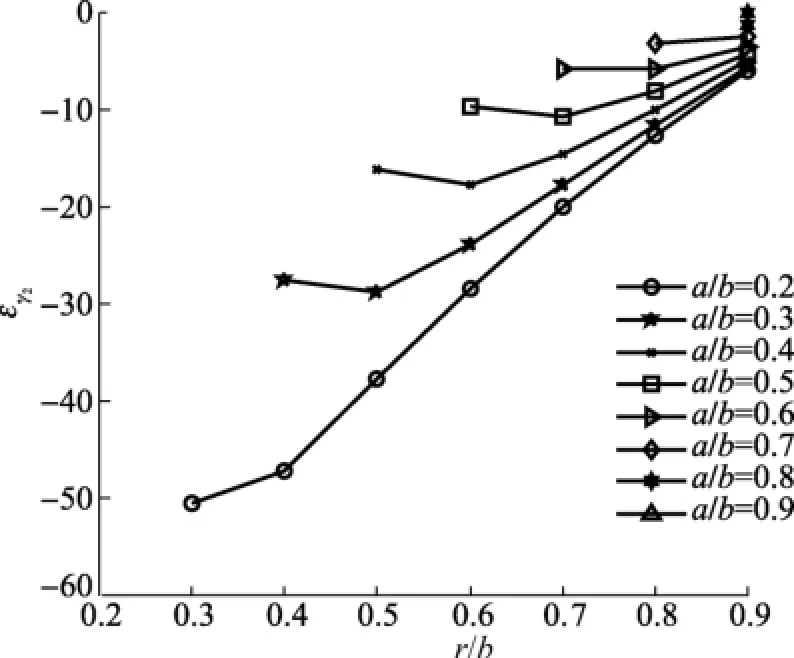
图5F2单独作用时εr2与r／b的关系

从图4、图5可得到：内外半径比a／b的比值越小，弹性体上的应变越大，灵敏度越高。在a／b＝0.2时，弹性体上的应变最大，由此确定传感器弹性体的内外半径比为a／b＝0.2。根据骨外固定器安装空间的限制，传感器不能太大，确定弹性体外半径b＝15mm，则内半径a＝3mm。

4.2 厚度h的优化

在考虑弹性体厚度h的优化时，由于弹性体的变形挠度很小，属于小挠度范围，则在轴向力及径向剪切力共同作用下弹性体的应力应变分析适用叠加原理，即通过分别算出轴向压力及径向剪切力单独作用下的应力应变后再进行叠加。当弹性体在轴向力F1作用下，根据式（2）、式（3）可以求出最大径向应力σr1max和最大切向应力σθ1max。最大径向应力和切向应力互相垂直，假设轴向力作用下弹性体表面上的最大应力为σ1max，且切向应力小于径向应力，则

式（15）中，σc为比例极限，以公式（15）作为h的优化目标。由式（2）、（3）、（7）、（8），弹性体上的最大应力出现在半径r＝3 mm和角度θ＝0°处。在传感器的工作范围内，最大轴向拉力为F1max＝70N，假设最大径向剪切力为F2max＝10 N，M＝0.04 N·m，由σmax≤σc，经计算得到：h≥0.817 6 mm。为了保证传感器具有一定的过载能力，且为了加工的方便，确定h＝1 mm。

5 应变片的贴片与组桥方式

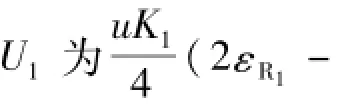
由于εR2比εR1大很多，同时2个应变方向相反，数值上没有正负的消减，因此，运算后的电压值最大，故这种组桥方式的输出电压最大。

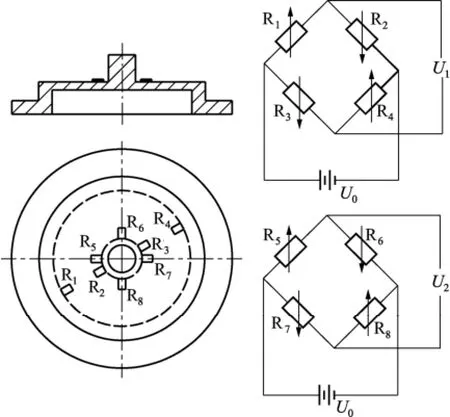
图6 应变片贴片位置及组桥方式示意图

图7 贴片后的传感器弹性体照片

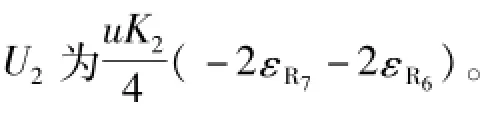
此时εR7和εR6符号相同，没有正负的消减，故桥路2的输出电压值是最大的，因此这种组桥方式的输出电压也是最大。

通过以上分析，图6的应变片组桥方式实现了对轴向力F1和径向力F2的动态解耦，同时也使得测量电桥的输出电压最大，保证了传感器具有较高的灵敏度。

6 传感器弹性体的标定实验

传感器弹性体的标定是通过实验测定的方法建立输入量和输出量之间的关系，标定过程采用“逐级加／卸载法”，分别施加和卸载两个单维力，对弹性体分别进行轴向力和径向力的标定。

标定实验装置包括动态应变仪、二维力传感器、标定装置、砝码、计算机。标定时将传感器固定在标定装置上，利用砝码进行加载和卸载，动态应变仪采集2组应变片桥路的输出。弹性体的标定曲线如图8至图11所示。从图8、图9可以看出：单独施加轴向压力时，测量径向剪切力的桥路2的输出接近于零。由图10、图11可以看出：单独施加径向剪切力时，测量轴向拉压力的桥路1的输出接近于零。说明传感器弹性体测量的轴向力与径向力之间的耦合很小，接近于零，达到了从贴片和组桥方式上实现二维力解耦的要求。

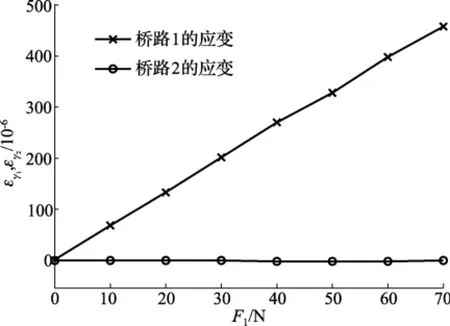
图8 轴向力的正向加载

图9 轴向力的反向加载

图10 径向力的正向加载

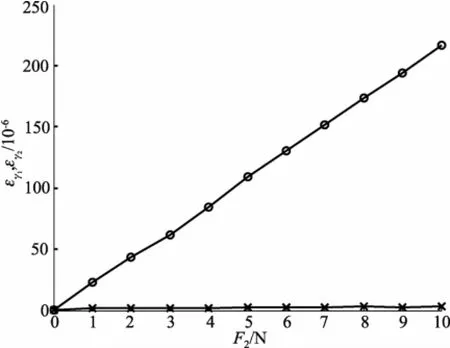
图11 径向力的反向加载

通过标定实验数据，经计算得到传感器的性能指标为：轴向力满量程非线性误差为1.1783%，径向力满量程非线性误差为1.0416%。轴向力测量重复性误差为0.7029%，径向力测量重复性误差为0.5012%，传感器灵敏度为2.9MPa／N。

7 结 论

研制了一种基于E型圆膜片式结构弹性体的微型二维力传感器，将其串接于骨外固定器中可实现对骨折愈合过程中创伤断面的二维应力状态进行实时检测。研制的微型二维力传感器的重量为47 g，最大半径为17mm。传感器体积小、重量轻，具有较高的灵敏度和测量精度，能满足骨折治疗中创伤断面应力测控系统的使用要求。

［1］ 孟和，顾志华.骨伤科生物力学［M］.北京：人民卫生出版社，2000，1－36.

［2］ 孟和.中国骨折复位固定器疗法［M］.北京：北京医科大学中国协和医科大学联合出版社，1993，60－95.

［3］ 王龙江，戴景兴，张磊，等.可动态检测骨折断端压力的单边加压外固定架的设计与测评［J］.中华创伤骨科杂志，2005，7（6）：541－543.

［4］ 杨俊英，李孟源，郭爱芳.微型S梁拉压力传感器的研制［J］.洛阳工学院学报，1998，19（3）：33－37.

［5］ 郭爱芳，李孟源，杨俊英.骨外固定横向力测量传感器的研制［J］.洛阳工学院学报，1999，20（2）：59－61.

［6］ 荣伟彬，王家畴，赵玉龙，等.基于MEMS技术的微操作三维力传感器研究［J］.仪器仪表学报，2007，28（4）：692－698.

［7］ Song A，Wu J，Qin G，etal．A novel self-decoupled four degree-of－freedom wrist force／torque sensor［J］.Measuremen，2007，40：883－891.

［8］ 崔维娜，王巍.一种新型水下机器人用六维腕力传感器［J］.仪器仪表学报，2001，22（4）：388－390.

［9］ Yao J，Hou Y，Chen J，etal．Theoretical analysis and experiment research of a statically indeterminate prestressed six-axis force sensor［J］.SensorsandActuators A：Physical，2009，150：1－11.

［10］ Liang Q，Zhang D，Song Q，etal．Design and fabrication of a six-dimensionalwrist force／torque sensor based on E-type membranes compared to cross beams［J］.Measurement，2010，43：1702－1719.

［11］ 杨卫超，余永，邓小红，等.一种基于双E型膜片的维小六维力传感器的设计［J］.仪器仪表学报，2008，21（7）：1137－1142.

［12］ 王鹏，付宜利，刘洪山，等.创伤手指康复外骨骼手关节力传感器研究［J］.传感器技术学报，2009，22（8）：1109－1113.

［13］ 雷运洪，吴正东，王建新，等.十字梁结构六维腕力传感器标定研究［J］.计量学报，2009，30（1）：34－37.

［14］ 郑红梅，刘正士，郑传荣，等.机器人六维腕力传感器标定试验台误差分析与研究［J］.计量学报，2005，26（4）：333－336，342.

［15］ 张晓辉，高峰.Stewart结构六维力传感器力矩各向同性研究［J］.计量学报，2005，26（1）：30－33，52.

［16］ 郑红梅，刘正士，王勇.机器人六维腕力传感器标定方法和标定装置的研究［J］.计量学报，2005，26（1）：43－45，85.

［17］ 金振林，张晓辉，高峰.Stewart型指尖力传感器结构尺寸对其灵敏度的影响研究［J］.计量学报，2004，25（3）：262－265.

［18］ 马弘跃，童淑敏，安珍.用于沙柳切削力检测的小型力传感器的设计与应用［J］.计量技术，2007，（12）：33－35.

Developm ent of Miniature Two-dim ensional Force Sensor for Fracture Trauma Cross-section

ZHU Jian-min， HUANG Zhi-wen， LIHai-wei， ZHAIDong-ting， WANG Jun
（School of Mechanical Engineering，University of Shanghai for Science and Technology，Shanghai200093，China）

Tomeet the real-time precisionmeasurement requirements of axial compressive force and radial shear force for fracture trauma cross-section，aminiature two-dimensional force sensor based on the E-type round diaphragm structure was designed.The theoretical analysismodel for sensor elastomer strain was established.Themain structure sizes of sensor elastomer were optimized according to the theoretical analysis model，and the strain gauge position and the combination bridgeways on the elastomer were designed.The calibration experiments for the sensor were carried out to obtain the calibration data.The experimental results show that the sensitivity of the sensor is 2.9 MPa／N，the full scale nonlinear error of axial force is 1.1783%，and the full scale nonlinear error of radial force is 1.0416%.

Metrology；Two-dimensional force sensor；Fracture trauma；Strain analysis；Elastomer；Calibration

TB931

A

1000-1158（2014）01-0061-06

10．3969／j．issn．1000-1158．2014．01．13

2012-09-20；

2013-01-28

国家自然科学基金项目（50975179）；上海市教委科研创新项目（11ZZ136）；上海市科委科研计划项目（1DZ2252300）

朱坚民（1968－），男，江苏如东人，上海理工大学教授，博士生导师。主要从事精密测量与智能控制的研究。jmzhu6688＠163.com