基于时频原子灰色关联的小电流接地故障选线方法

王晓卫,侯雅晓,田 书,李玉东,高 杰,魏向向

(河南理工大学电气工程与自动化学院,河南焦作 454000)

基于时频原子灰色关联的小电流接地故障选线方法

王晓卫,侯雅晓,田 书,李玉东,高 杰,魏向向

(河南理工大学电气工程与自动化学院,河南焦作 454000)

提出一种时频原子灰色关联的小电流接地故障选线方法。根据当前小电流接地系统分支线路数目,计算故障线与非故障线的线路基准值;以Gabor原子库为索引,利用匹配追踪法将各分支线路故障后首个1/4周期内的暂态零序电流进行时频原子分解,求得表征各分支线路故障特征信息的衰减正弦量原子;采用改进灰色关联分析对各衰减正弦量原子进行关联度分析,求得各分支线路的特征值;将各特征值分别与故障线和非故障线的基准值求欧式距离并比较大小,通过所求欧式距离大小的比较,可实现准确选线。仿真结果表明,该方法计算量小,选线精度高,尤其适用于多分支线路的小电流接地系统。

匹配追踪;衰减正弦量原子;灰色关联;欧氏距离;区间域

目前,对于小电流接地系统故障选线问题,众多学者提出了多种故障选线方法。主要采用S变换[1]、希尔伯特-黄变化(HHT)[2]、普罗尼(Prony)算法[3]、分形理论[4]、经验模态分解(EMD)[5]、遗传算法[6]等信号处理工具提取信号,然后采用神经网络[7]、支持向量机[8]、贝叶斯分类法[9]、信息熵[10]、Hough变换[11]等建立选线判据。

S变换是对连续小波变换和短时傅里叶变化的发展,具有良好的时频特性,但分解后信息量太多。HHT与Prony算法能够得到解析的信号分解形式,但这2种算法均不能表达不连续的信号。分形理论需要选择恰当的分形维数以描述其特征,分形维数选择不当时,会增加运算量,增大误差。EMD适合分析非线性、非平稳时间序列信号,但当信号的采样频率过低时,容易造成虚假模态和模态混叠频繁出现等问题。遗传算法具有自适应性,其鲁棒性强,便于并行处理,但退化现象明显,可变的灵活程度较小。神经网络存在局部最优问题,且收敛性较差,训练时间较长,可靠性有限。支持向量机在解决小样本、非线性及高维模式识别问题中具有优势,但识别能力易受自身参数的影响。贝叶斯分类法需要已知确切的分布概率,而实际上并不能给出确切的分布概率。信息熵可用来描述一个变量的不确定性,但需有足够多的数据作为依据,才能有效判别信号所具有的特征。Hough变换在参数空间不超过2维的情况下,有优异的表现,但若参数空间增大,其计算量急剧上升,同时耗费巨大的存储空间,耗时也随之猛增。

本文提出一种时频原子(time-frequency atom decomposition,TFAD)灰色关联(greycorrelation analysis,GCA)的小电流接地故障选线方法[12-16],该方法将测得的暂态零序电流进行时频原子分解,构建出表征暂态零序电流的衰减正弦量原子,再经改进灰色关联分析求得各线路的特征值,与计算好的线路基准值进行欧氏距离求解,最后,通过比较欧式距离大小,判定故障发生线路。

1 暂态零序电流分析

单相接地暂态零序等值电路如图1所示,其中, C0为线路零序电容;L0为线路零序等值电感;Rg为接地点的过渡电阻;Rp和Lp分别为消弧线圈的等效电阻和电感;e(t)为零序电压。

在补偿电网中发生故障的瞬间,由图1可得流过故障点的暂态零序电流为

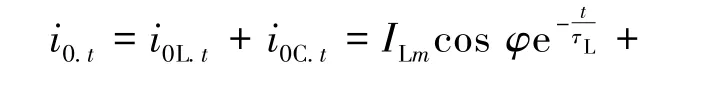
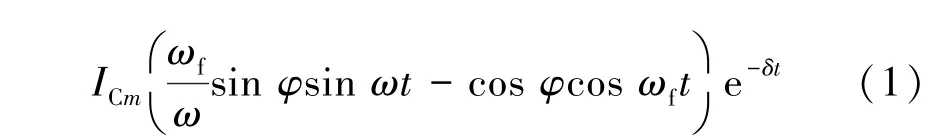
式中,i0L．t为暂态零序电流中的电感电流分量;i0C．t为暂态零序电流的电容电流分量;ILm和ICm分别为电感电流和电容电流的初值;ω为工频角频率;ωf和δ分别为暂态零序电流容性分量的振荡角频率和衰减系数;τL为电感电流的衰减时间常数;φ为接地时故障线路相电压的初始相位。

图1 单相接地暂态零序等值电路Fig．1 Transient zero sequence equivalent circuit of single-phase to ground

振荡角频率ωf和衰减系数δ分别为

由式(1)可以得知,暂态零序电流由正弦函数分量组合而成,并且其波形具有衰减特性。由式(2),(3)分别可知,振荡角频率ωf受L0,C0,Rg的影响,衰减系数δ受L0,Rg影响,并且可以得出,随着过渡电阻Rg数值的增大,ωf减小,δ增大,反映在实际中,表现为暂态零序电流波形振荡趋势变缓,衰减较快,暂态过程将很快结束并进入到稳态。因此,能在大电阻接地故障时准确提取出暂态分量并实现精确选线,将是检验故障选线方法适用性的重要指标。

图2为某实际配电网架空线路1单相接地故障时测得的各条线路的暂态零序电流,从图2可以看出,不管是架空线路,电缆线路,还是缆线混合线路,其暂态零序电流均具备振荡衰减特征。

2 理论分析

2.1 TFAD原理

传统的信号分解算法主要有傅里叶变换和小波变换,但这2种算法所表示信号的能力和范围具有一定的局限性。针对此现状,本文引入TFAD算法[18],该算法能够将故障时各分支线路的暂态零序电流信号进行自适应分解,最后用一系列时频原子的线性叠加来表示暂态零序电流。它可用于提取信号中的瞬态冲击响应特征[19]。

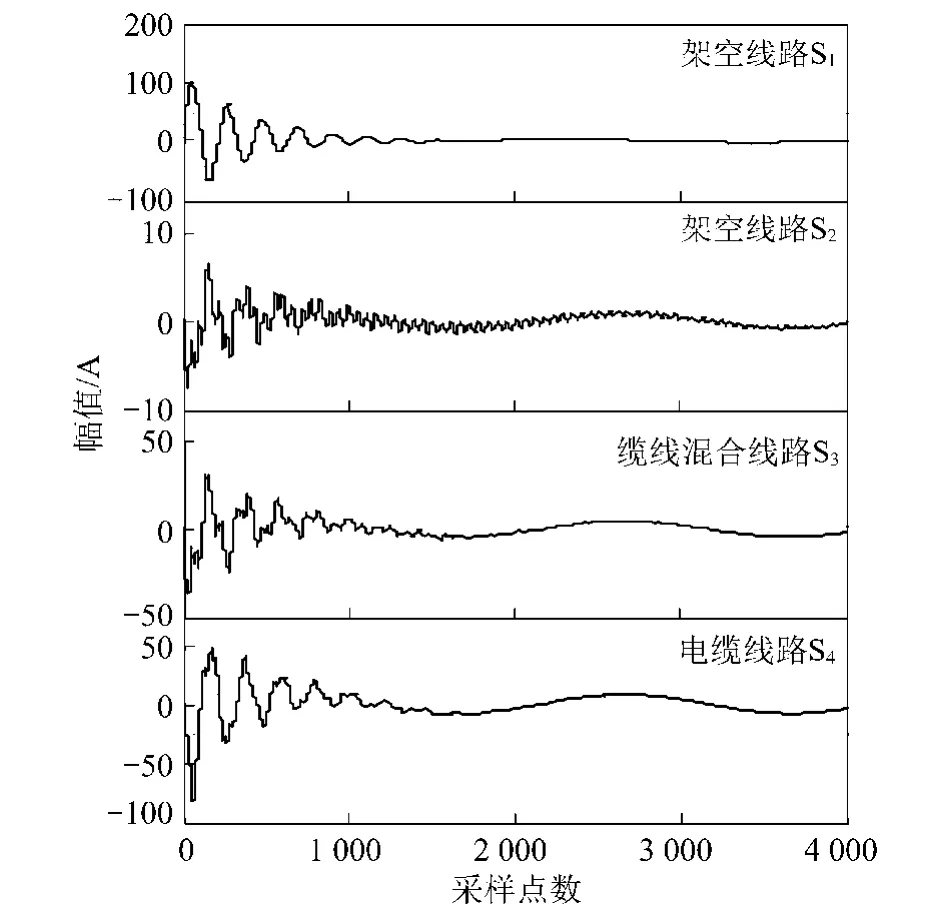
图2 暂态零序电流Fig．2 Transient zero sequence current

设信号为X,D为过完备的原子库,g为原子库中经归一化的原子(‖g‖=1),信号分解时,在过完备原子库D中选择与信号X最匹配的原子,其选择原则为内积最大,设第1个最匹配原子为g1。则

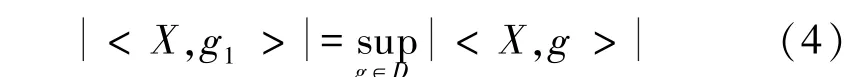
式中,〈·,·〉表示两者的内积。

已知原子满足归一化条件,因此,信号X可以分解为2部分：原子g1上的分量和残差c1,即

接着对每次匹配的残差进行分解,直到达到终止条件为止,若对信号分解了M次,则信号可以表示成

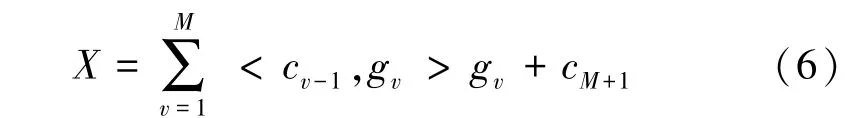
为达到信号稀疏分解的目的,将暂态零序电流分解成一系列原子信号的线性组合,而这些原子是从一个冗余的原子库中选取的。为了使选取的原子最佳地匹配原始信号的特征,TFAD算法采取一种自适应的分解策略。

在处理信号的过程中,TFAD算法有它特定的级联原子库,只有选择合适的级联原子库才能对所分析的信号进行精确分析。本文采用最基本的Gabor原子库来分析信号,Gabor原子表达式为

式中,g(t)=21/4e-πt2为高斯窗函数;定义索引γ=(s, τ,ξ,φ),其中,s为尺度参数,τ为位移参数,ξ为频率因子,φ为相位因子。

由于式(7)是一个连续函数,故所得到的原子空间库是无穷的,在实际中不可能搜索一个无穷的空间,所以对原子库进行离散处理。令

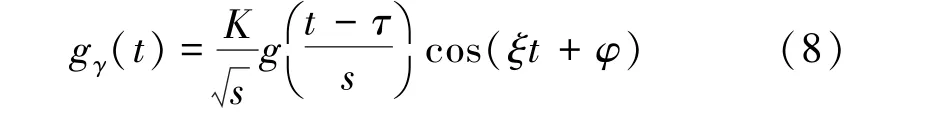
式中,K是信号幅值归一化的系数。

可见,Gabor原子实质上是由正弦函数调制后的高斯窗函数构成的。令待分析暂态零序电流信号的长度为N,则对索引γ=(s,τ,ξ,φ)进行离散化处理后可得γ=(2λ,p2λ,kπ21-λ,φ),其中,λ,p,k∈Z,φ∈R,且参数λ,p,k可满足如下关系

通过对Gabor原子库进行时频分析可以发现, Gabor原子库的时频分布为一椭圆[20],其时频聚集性相对较弱。而在电力系统中,暂态零序电流的特征频带会随着电网结构、故障模式等因素而处于不同区域,且特征频带内不同频率暂态电流信号在时间段上的分布也各不相同[21]。故不能直接由Gabor原子库来分析暂态零序电流,需要和其他原子相互配合。因此,为能够对暂态零序电流进行分析与处理,还需建立一个符合电网暂态零序电流的原子。

2.2 暂态零序电流衰减正弦量原子求解

由上文可知,暂态零序电流经Gabor原子库分解之后,需建立一个适合分析电网信号的暂态零序电流衰减正弦量原子,并对其做进一步分析。

由暂态零序电流的特性可知,其波形具备振荡衰减的趋势,因此,本文采用衰减正弦量原子来拟合故障后的暂态零序电流,暂态零序电流衰减正弦量原子的构造为

式中,每一个衰减分量都有固定的时间支撑区且包含6个参数(Aq,fq,αq,φq,ts,te),其中,Aq为最大幅值; fq为频率;αq为衰减因子;φq为相位;ts与te分别为暂态零序电流的起始时刻和终止时刻;u(t)为单位阶跃函数。

以Gabor原子库为索引,按匹配追踪(matching pursuit,MP)算法对暂态零序电流进行分析处理之后,可得到其最佳原子gγ和最优4参变量(s,τ,ξ, φ)[22],进而可求得暂态零序电流衰减正弦量原子的基本参数,具体实现过程如下。

(1)利用MP算法将暂态零序电流在Gabor过完备原子库中进行稀疏分解,得到第一个最匹配原子gγ0。

(2)每次迭代时将新原子与残差信号做内积计算,同时对4参变量(s,τ,ξ,φ)按顺序进行优化。

(3)当内积增加值不足当前的1%,或当前参变量的增加值不足自身值的10%时,迭代终止。

(4)程序运行结束,得到最佳原子gγ以及其最优4参变量(s,τ,ξ,φ)。

(6)根据“从大到小”的排序方法,寻找最佳原子gγ幅值的最大值,即为衰减正弦量原子gi(t)的最大幅值Aq。

由以上6步可求得原子的最大幅值Aq、衰减因子αq,以及暂态零序电流的最优4参变量(s,τ,ξ, φ)。由暂态零序电流的最优4参变量(s,τ,ξ,φ),可求得暂态零序电流衰减正弦量原子参数中的频率因子fq和相位因子φq(fq=ξ,φq=φ)。

2.3 改进的GCA

传统的灰色关联度只考虑事物间静态差值之间的关联[24],若从动态的角度来衡量,如波形曲线的变化率和斜率,则需利用曲线的几何形状变化趋势来计算关联度。因此,本文定义一种适合分析暂态零序电流关联度的计算式。

设有2个暂态零序电流信号Xi(t)(代表参考信号),Xj(t)(代表比较信号)。这样,在关联分析中,参考信号Xi(t)和比较信号Xj(t)的关联度计算如下

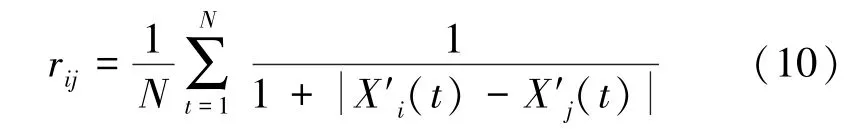
式中,X′i(t),X′j(t)分别为信号Xi(t)和Xj(t)对时间t的导数。

假设小电流接地系统具有n条分支线路,线路编号分别为1,2,…,n,当系统发生故障时,通过采样装置获得各分支线路的暂态零序电流,然后利用式(10)可计算各分支线路间的灰色关联度rij。其中,n条分支线路共计算次,即可获得该小电流接地系统的关联度矩阵R[25]为

关联度矩阵R中的每一元素rij均表示第i条线路和第j条线路之间暂态零序电流的关联程度,据此,可计算出第i条线路与其余的n-1条线路的平均关联度为

3 分支线路基准值求解

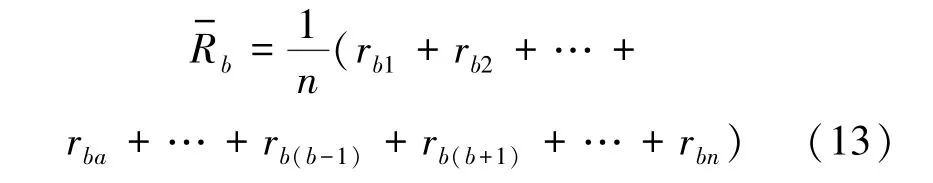
暂态零序电流特征：对于实际的小电流接地系统,各条非故障线路之间的暂态零序电流波形相似,而故障线与非故障线之间的暂态零序电流波形差异大[26]。故得出：

(1)任意2条非故障线路间的暂态零序电流关联度数值相似度极高,即近似相等;

(2)故障线路与任1条非故障线路间的暂态零序电流关联度数值相似度极高,即近似相等;

(3)故障线路与非故障线路间暂态零序电流关联度数值与任2条非故障线路间的暂态零序电流关联度数值相似度差,即不相等。

由此,式(13)中具备如下关系其中,rbn表示任意2个非故障线路之间的关联度;rab表示1条故障线与1条非故障线之间的关联度。当小电流接地系统的分支线路数n确定时,影响式(14)结果的仅有2个变量rbn和rba,由上述设定可知,rbn和rab的值不随n和b的变化而变化,故可得各条非故障线路的平均关联度的大小与b无关。

因此,各分支线路的平均关联度具有以下关系

由此,根据式(12),可得

(1)故障线路的平均关联度差值之和为

(2)非故障线路的平均关联度差值之和为

因此,故障线路与非故障线路的平均关联度差值之和满足如下关系

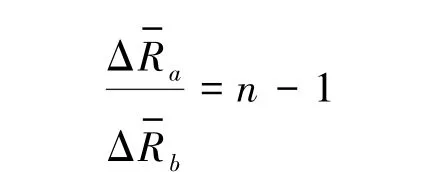
式中,0≤a,b≤n。

为量化各线路的固有特性,本文提出线路基准值概念,定义：将分支线路i的平均关联度差值和与其他分支线路平均关联度差值和的比值称之为线路i的基准值,其计算式如下

上述基准值只与线路分支数n有关,因此,只要知道小电流接地系统中的线路条数,即可求得表征故障线路与非故障线路物理特征的基准值Ja,Jb。

4 故障选线机制及流程

4.1 选线机制

为分析分支线路的属性及其动态特征,本文提出线路特征值和区间域的概念。

(1)特征值。将各分支线路衰减正弦量原子gi(t),gj(t)对应的平均关联度差值和之比定义为线路特征值Ti。具体的求解如图3所示。

图3 特征值Ti的求解Fig．3 Calculation of proper value Ti

(2)区间域。将在水平数轴上属于基准值Ja,Jb的所有特征值的集合分别定义为Ja,Jb的区间域,也即故障线与非故障线区间域。以线路n=3,4为例,由式(16),(17)可得：当n=3时,Ja=4,Jb=1．5;当n=4时,Ja=9,Jb=2．33,则各自的区间域如图4所示。

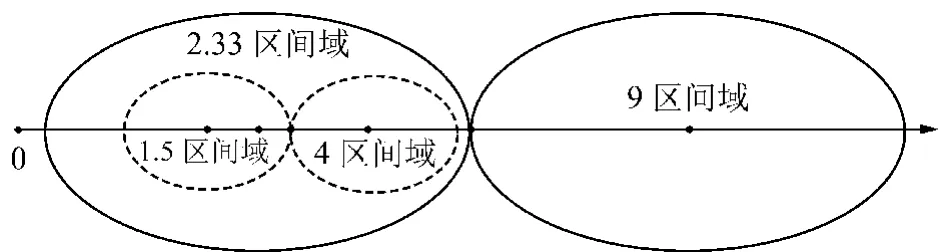
图4 区间域Fig．4 Interval domain

如图4所示,若所求分支线路特征值Ti的数值落于故障线路基准值Ja的区间域,则判定第i条分支线路具备故障线路属性,反之,则具备非故障线路属性。

另外,随着小电流接地系统中分支线路数的增多,故障线与非故障线区间域总体覆盖范围Δ显著增大,如图4所示：当n=3时,总体覆盖范围：Δ=(4-1．5)×2=5;当n=4时,总体覆盖范围：Δ=(9-2．33)×2=13．34,反映在实际的故障选线系统中,总体覆盖范围的增大,使得所求得的特征值Ti落在各自基准值Ja,Jb区间域的概率大大增加,更利于实现准确选线,也即,随着小电流接地系统中分支线路数的增多,该选线方法更有利于准确选线。

欧氏距离可度量分类对象之间的接近与相似程度。在此,为分析各条分支线路的特征值与基准值之间的关系,将Ti与Ja,Jb分别求欧氏距离,具体计算为

式中,Via,Vib分别为第i条线路的特征值Ti与线路基准值Ja,Jb之间的欧氏距离。

实际应用中,通过比较Via和Vib的大小以实现故障线路的精确判断,具体如下：若Via＜Vib,则Ti落到了Ja的区间域,由此判定第i条线路为故障线路;若Via≥Vib,则Ti落到了Jb的区间域,判定第i条线路为非故障线路。

4.2 选线步骤及流程

为实现小电流接地系统的故障选线,本文方法的具体步骤如下。

(1)当系统零序电压大于0．15倍的母线额定电压时,分别检测TV与消弧线圈是否发生断线与串联谐振,若TV未发生断线,且消弧线圈也未发生串联谐振,则判定小电流接地系统发生故障,同时启动采样装置,记录各分支线路故障发生时刻起首个1/4周期内的暂态零序电流信号。

(2)根据当前小电流接地系统分支线路数目,计算故障线与非故障线的线路基准值Ja,Jb。

(3)以Gabor原子库为索引,利用MP算法对各分支线路的暂态零序电流进行时频原子分解,获得各分支线路对应的最优4参变量(s,τ,ξ,φ)和最佳原子gγ。

(4)利用4参变量(s,τ,ξ,φ)和gγ确定暂态零序电流衰减正弦量原子参数,进而求得该小电流接地系统中第i条线路与其余n-1条线路的衰减正弦量原子关联度rij。

(5)由衰减正弦量原子关联度rij,求得小电流接地系统的线路关联度矩阵R,进而求得分支线路的特征值Ti。

(6)求出各分支线路的2个欧氏距离Via和Vib,并比较大小。若Via＜Vib,判定第i条分支线路为故障线路,选线结束;若Via≥Vib,判定第i条分支线路为非故障线路,继续检测下一条线路。

(7)当所有分支线路均被判定为非故障线路时,则可判定母线发生故障。

具体的选线流程如图5所示。

5 算例分析

图5 选线流程Fig．5 Flow chart of line selection

线路S1,S2为架空线路,线度长度分别为13．5, 24．0 km,线路正序参数为R1=0．17 Ω/km,L1= 1．2 mH/km,C1=9．697 nF/km,零序参数为R0= 0．23 Ω/km,L0=5．48 mH/km,C0=6 nF/km。线路S4为电缆线路,长度10 km,线路正序参数为R1= 0．193 Ω/km,L1=0．442 mH/km,C1=143 nF/km;零序参数为R0=1．93 Ω/km,L0=5．48 mH/km,C0= 143 nF/km。线路3为缆线混合线路,其中电缆线长度为5 km,架空线路长度为12 km;消弧线圈L的过补偿度为10%,消弧线圈的电感值经计算为1．574 H。

其中,消弧线圈的电阻值取电抗值的10%,经计算为48．576 Ω。仿真模型如图6所示。

以线路S1发生单相接地故障,初相角0°,接地电阻Rf=5 Ω的情况为例进行分析。采样频率f= 105Hz,仿真时长0．06 s,故障发生时刻设定为0．02～0．04 s。

图6 中性点经消弧线圈接地系统故障仿真Fig．6 Fault simulation of the neutral point arc suppression coil

5.1 衰减正弦量原子参数计算

根据所述方法,当S1发生故障时,利用Gabor原子库分别求出各分支线路暂态零序电流的最优4参变量(s,τ,ξ,φ)以及最佳原子波形分别如表1及图7所示。

表1 分支线路的最优4参变量Table 1 The optimal 4 parameters of branch lines

图7 各条线路暂态零序电流最佳原子Fig．7 Best atoms of transient zero sequence current

由表1数据可求出衰减正弦量原子的参数。由前文可知,衰减正弦量原子共需确定6个参数(Aq, fq,αq,φq,ms,me),其中,所需的频率因子fq和相位因子φq与经Gabor原子库分解后得到ξ和φ大小相等。另外,开始与终止的采样时刻可根据总的采样点数与采样频率计算得出。故只需计算衰减正弦量原子参数中的幅值Aq及衰减因子αq。

由图7可知,各分支线路暂态零序电流的最佳原子具有衰减特性,故采用求衰减系数αq,同时,求得暂态零序电流衰减正弦量原子的最大模值Aq。所得暂态零序电流衰减正弦量原子的参数见表2。

表2 暂态零序电流衰减正弦量原子参数Table 2 The decay sinusoidal atom parameters of transient zero sequence current

根据表2数据,可构建初相角0°,接地电阻5 Ω,线路S1发生故障时,各分支线路的衰减正弦量原子表达式为

5.2 特征值求解

对式(20)中的每条分支线路的衰减正弦量原子求导,并利用式(10)求出第i条线路与第j条线路之间的关联度rij,以此为基础,求得算例中各线路间的衰减正弦量原子关联度矩阵R为

由于算例中具有4条分支线路,即n=4,故由式(16),(17)可知：故障线路与非故障线路的基准值分别为：Ja=9,Jb=2．33。

利用式(18),(19)分别计算欧氏距离Via和Vib并比较其大小。当Via＜Vib时,判定第i条线路为故障线路;当Via≥Vib时,判定第i条线路为非故障线路。所得结果见表3。

表3 线路S1故障时选线结果Table 3 Selection results of line S1fault

由表3可知,判定结果准确。为全面验证本文方法的正确性,在不同线路,不同故障初相角及接地电阻值的情况发生故障,所得各条分支线路的特征值见表4。

表4 架空线路S1,S3,S4和母线故障Table 4 Overhead line S1,S3,S4and bus fault

限于篇幅,以表4中S1的数据为例,求得4条分支线路在不同故障情况下的欧氏距离Via与Vib,在此,为表述方便,取纵坐标为Via-Vib,则分析结果如图8所示。

图8 架空线路S1故障时V1a与V1b关系Fig．8 The relation of V1aand V1bin overhead line S1fault

观察图8可知,在不同故障条件下,线路S1的V1a-V1b＜0恒成立,即V1a＜V1b成立,故可判定S1为故障线路。线路S2,S3,S4的Via-Vib＞0(i=2,3, 4)恒成立,即Via＞Vib成立,可判定S2,S3,S4为非故障线路。同理,对表4中S3,S4的数据做同样处理,也可准确地判定出故障发生的线路。对于母线故障而言,表4所求得的欧氏距离均满足：Via-Vib≥0(i=1,2,3,4),由此,可判定出4条分支线路均为非故障线路,那么故障此时必发生在母线上,判定结果准确。

由上述分析可知,本文方法特别适合于分支线路数目较多的小电流接地系统,当分支线路数目大于3条以上时,能准确判定出故障发生线路。

6 结 论

(1)将暂态零序电流经TFAD算法分解,构建出的衰减正弦量原子,能精确表征各分支线路的故障特征,较之其他算法,TFAD不仅能有效提取模态参数,而且具备时间量定位功能,能够处理非连续信号。

(2)改进GCA理论紧紧抓住了各分支线路间的暂态零序电流特征,通过推导,本文得出了故障线与非故障线的基准值,该数值只与线路数目有关,计算简便,并且随着线路数的增多,其区间域总体覆盖范围增大,更利于准确选线。

(3)欧式距离的大小可有效衡量两个数值之间的相似程度,距离越近就越相似,通过欧式距离大小的判断,可较好地实现故障线与非故障线的有效分类,欧式距离的求解,计算量小,便于在实际的选线装置中进行应用。

[1] 张 钧,何正友,贾 勇．基于S变换的故障选线新方法[J]．中国电机工程学报,2011,31(10)：109-155．

Zhang Jun,He Zhengyou,Jia Yong．Fault line identification approach based on S-transform[J]．Proceedings of the CSEE,2011,31(10)： 109-155．

[2] 杨德昌,C Rehtanz,李 勇．基于改进希尔伯特-黄变换算法的电力系统低频振荡分析[J]．中国电机工程学报,2011,30(10)： 102-108．

Yang Dechang,C Rehtanz,Li Yong．Researching on low frequency oscillation in power system based on improved HHT algorithm[J]．Proceedings of the CSEE,2011,30(10)：102-108．

[3] 王晓卫,吴继维,李然月．基于Prony相对熵的故障投票选线新方法[J]．中国电力,2013,46(1)：59-65．

Wang Xiaowei,Wu Jiwei,Li Ranyue．A novel method of fault selection based on voting mechanism of prony relative entropy theroy[J]．Electric Power,2013,46(1)：59-65．

[4] 杜延辉．多重分形和小波理论在小电流接地系统单相接地故障选线中的应用研究[D]．成都：西南交通大学,2008．

[5] 张淑清,翟欣沛,董 璇．EMD及Duffing振子在小电流系统故障选线方法中的应用[J]．中国电机工程学报,2013,33(10)： 161-167．

Zhang Shuqing,Zhai Xinpei,Dong Xuan．Application of EMD and duffing oscillator to fault line detection in un-effectively grounded system[J]．Proceedings of the CSEE,2013,33(10)：161-167．

[6] 郭壮志,陈 波,刘灿萍．基于遗传算法的配电网故障定位[J]．电网技术,2007,31(11)：87-92．

Guo Zhuangzhi,Chen Bo,Liu Canping．Fault location of distribution network based on genetic algorithm[J]．Power System Technology,2007,31(11)：87-92．

[7] 林 圣,何正友,臧天磊．基于粗神经网络的输电线路故障分类方法[J]．中国电机工程学报,2010,30(28)：72-79．

Lin Sheng,He Zhengyou,Zang Tianlei．Novel approach of fault type classification in transmission lines based on rough membership neural networks[J]．Proceedings of the CSEE,2010,30(28)：72-79．

[8] 张全明,刘会金．最小二乘支持向量机在电能质量扰动分类中的应用[J]．中国电机工程学报,2008,28(1)：106-110．

Zhang Quanming,Liu Huijin．Application of LS-SVM in classification of power quality disturbances[J]．Proceedings of the CSEE, 2008,28(1)：106-110．

[9] 李 强,徐建政．基于主观贝叶斯方法的电力系统故障诊断[J]．电力系统自动化,2007,31(15)：46-49．

Li Qiang,Xu Jianzheng．Secondary voltage control considering network transmission delays[J]．Automation of Electric Power Systems, 2007,31(15)：46-49．

[10] 李天云,王 飞,祝 磊．基于固有模态能量熵的配电网单相接地故障选线新方法[J]．电网技术,2008,32(2)：128-132．

Li Tianyun,Wang Fei,Zhu Lei．A new method of distribution network single-phase ground fault line selection based on the intrinsic mode energy entropy[J]．Power System Technology,2008, 32(2)：128-132．

[11] 束洪春,高 利,段锐敏．利用零序电流全量Hough变换的配电网故障选线方法[J]．电力系统自动化,2013,37(9)：1-7．

Shu Hongchun,Gao Li,Duan Ruimin．A novel hough transform approach of fault line selection in distribution networks using the total zero-sequence current[J]．Automation of Electric Power Systems, 2013,37(9)：1-7．

[12] Wu Xueming,Yu Dejie．Atomic decomposition method based on adaptive chirplet dictionary[J]．Advances in Adaptive Data Analysis,2012,4(1)：1-19．

[13] Mallat Stephane,Zhang Zhifeng．Matching pursuit with time-frequency dictionaries[J]．IEEE Transactions on Signal Processing, 1993,41(12)：3397-3415．

[14] Lisandro Lovisolo,Michel P Tcheou,Eduardo A B da Silva．Modeling of electric disturbance signals using damped sinusoids via atomic decompositions and its applications[A]．EURASIP Journal on Advances in Signal Processing[C]．2007：1-15．

[15] Lisandro Lovisolo,Eduardo A B da Silva,Marco A M Rodrigues．Efficient coherent adaptive representations of monitored electric signals in power systems using damped sinusoids[J]．IEEE Transactions on Signal Processing,2005,53(10)：3831-3846．

[16] 罗 毅,李昱龙．基于熵权法和灰色关联分析的输电网规划方案综合决策[J]．电网技术,2013,37(1)：77-81．

Luo Yi,Li Yulong．Comprehensive decision-making of transmission network planning based on entropy weight and grey relational analysis[J]．Power System Technology,2013,37(1)：77-81．

[17] 赵化时,姚李孝,柯丽芳．配电网选线和测距新方法研究[J]．电力系统保护与控制,2010,38(16)：6-10．

Zhao Huashi,Yao Lixiao,Ke Lifang．A novel method for fault line selection and location in distribution system[J]．Power System Protection and Control,2010,38(16)：6-10．

[18] Mark R McClure,Lawrence Carin．Matching pursuits with a wavebased dictionary[J]．IEEE Transations on Signal Processing,1997, 45(12)：2912-2926．

[19] 贾清泉,于连富,董海艳．应用原子分解的电能质量扰动信号特征提取方法[J]．电力系统自动化,2009,33(24)：68-71．

Jia Qingquan,Yu Lianfu,Dong Haiyan．Power quality disturbance features extraction based on atomic decomposition[J]．Automation of Electric Power Systems,2009,33(24)：68-71．

[20] 朱 明,金炜东,胡来招．基于原子分解的辐射源信号二次特征提取[J]．西南交通大学学报,2007,42(6)：659-664．

Zhu Ming,Jin Weidong,Hu Laizhao．Cascade feature extraction for radar emitter signals based on atomic decomposition[J]．Journal of Southwest Jiao Tong University,2007,42(6)：659-664．

[21] 张大波．复小波变换在小电流单相接地故障选线中的应用研究[D]．成都：西南交通大学,2007．

[22] 李 勋,龚庆武,贾晶晶．基于原子稀疏分解的低频振荡模态参数辨识方法[J]．电工技术学报,2012,27(9)：124-133．

Li Xun,Gong Qingwu,Jia Jingjing．Atomic sparse decomposition based identification method for low-frequency oscillation modal parameters[J]．Transactions of China Electrotechnical Society,2012, 27(9)：124-133．

[23] 王 宁,李林川,贾清泉．应用原子分解的电能质量扰动信号分类方法[J]．中国电机工程学报,2011,31(4)：51-58．

Wang Ning,Li Linchuan,Jia Qingquan．Classification of power quality disturbance signals using atomic decomposition method[J]．Proceedings of the CSEE,2011,31(4)：51-58．

[24] 王 韶,朱姜峰．基于改进相关性分析法的配电网络单相接地故障选线[J]．电力系统保护与控制,2012,40(15)：76-81．

Wang Shao,Zhu Jiangfeng．Faulty line selection of single-phase to ground fault in distribution network based on improved correlation analysis method[J]．Power System Protection and Control,2012, 40(15)：76-81．

[25] 张慧芬,潘贞存,田质广．基于可辨识矩阵的单相接地故障选线新方法[J]．中国电力,2006,39(11)：33-36．

Zhang Huifen,Pan Zhencun,Tian Zhiguang．Discernable matrix method based method for detecting single phase grounding feeder[J]．Electric Power,2006,39(11)：33-36．

[26] 束洪春．电力工程信号处理应用[M]．北京：科学出版社,2009．

A novel fault line selection method based on time-frequency atom decomposition and grey correlation analysis of small current to ground system

WANG Xiao-wei,HOU Ya-xiao,TIAN Shu,LI Yu-dong,GAO Jie,WEI Xiang-xiang

(School of Electrical Engineering and Automation,Henan Polytechnic University,Jiaozuo 454000,China)

This paper proposed a small current to ground fault line selection method with time-frequency atom and grey correlation analysis．Firstly,it calculated the base values of fault line and non-fault line based on the number of branch line of small current to ground system．Secondly,it used the matching pursuit method to decompose the transient zerosequence current of the first 1/4 cycle indexed by Gabor atom,and calculated the damped sinusoidal atoms of every branch line which expressed the characteristic of fault state．Thirdly,it used the theory of grey relational analysis to compute the correlation degree of every damped sinusoidal atom,and got the characteristic value of every branch line．Finally,it calculated the Euclidean distance value between the characteristic values and the base values of fault line and non-fault line,and compared the size of Euclidean distance values to achieve the fault line selection accurately．The method has a lower computational complexity,an accurate fault selection proved by a large number of simulations．It is especially suitable for the multi-branch lines of small current to ground system．

matching pursuit;damped sinusoidal atom;grey correlation;Euclidean distance;interval domain

TD611

A

0253-9993(2014)10-2147-10

2013-10-18 责任编辑：许书阁

国家自然科学基金资助项目(61403127);河南省教育厅科学技术研究重点资助项目(12B470002,14A470004)

王晓卫(1983—),男,陕西凤翔人,讲师,硕士。E-mail：proceedings@126．com

王晓卫,侯雅晓,田 书,等．基于时频原子灰色关联的小电流接地故障选线方法[J]．煤炭学报,2014,39(10)：2147-2156．

10．13225/j．cnki．jccs．2013．1493

Wang Xiaowei,Hou Yaxiao,Tian Shu,et al．A novel fault line selection method based on time-frequency atom decomposition and grey correlation analysis of small current to ground system[J]．Journal of China Coal Society,2014,39(10)：2147-2156．doi：10．13225/j．cnki．jccs．2013．1493