改进的岩石Burgers流变模型及其试验验证
徐 鹏,杨圣奇,陈国飞
(中国矿业大学深部岩土力学与地下工程国家重点实验室,江苏徐州 221008)
改进的岩石Burgers流变模型及其试验验证
徐 鹏,杨圣奇,陈国飞
(中国矿业大学深部岩土力学与地下工程国家重点实验室,江苏徐州 221008)
为了准确描述不同轴压下岩石流变过程中的瞬时应变变化规律,提出一种用于描述岩石流变试验中瞬时塑性应变变化规律的裂隙塑性元件,将该元件与传统Burgers模型相结合组成改进的Burgers模型,给出了模型加卸载流变方程,对该模型的蠕变特性进行了分析。对莒山矿粉砂岩进行瞬时三轴压缩试验,得到试样在不同围压下全应力-应变曲线,给出了围压与峰值强度的线性关系,对粉砂岩试样进行多级增量循环加卸载流变试验,对试验数据进行辨识和分析,结果表明:瞬时塑性应变在模型参数辨识过程中不能忽略。使用改进的Burgers模型对不同应力水平条件下粉砂岩加卸载流变试验结果进行了拟合,效果较为理想,同时与传统Burgers模型对试验数据的拟合效果进行比较,验证了改进模型的正确性和合理性。
改进的Burgers流变模型;瞬时塑性应变;裂隙塑性元件
岩石的流变特性是指岩石在外界荷载、温度、辐射等条件下呈现的与时间有关的变形、流动和破坏等性质,即时间效应。其主要表现在弹性后效、蠕变、松弛、应变率效应、时效强度和流变损伤断裂等方面,流变变形是岩石的基本力学特性,岩石流变是岩土工程围岩变形失稳的重要原因之一[1-3]。
近年来,人们在岩石的蠕变试验研究及其本构模型建立方面,取得了不少成果。夏才初等[4-5]通过分析不同应力水平下加卸载流变试验过程中的弹性、塑性和黏性等流变性态,提出了统一流变力学模型[4],该模型及其导出的15个退化模型可以包含所有的理论流变模型及其等效模型,根据流变过程中各性态试验参数的提取,给出了模型参数的确定方法[5]。
随着流变理论的发展,许多研究者提出了流变模型中的一个或几个模型参数不是常数而是应力或时间或两者函数的参数非线性流变力学模型。杨圣奇等[6]通过对龙滩水电站泥板岩的剪切流变特性的研究,提出了岩石非线性剪切流变模型,用于描述加速流变过程。邓荣贵等[7]通过研究岩石的蠕变试验数据,提出了一种非线性黏滞阻尼器,并将该元件与传统元件组合构成复合模型。徐卫亚等[8]通过分析绿片岩加速流变阶段中损伤量的变化,在衰减和稳态蠕变阶段引入一非线性函数,在加速蠕变阶段引入损伤,建立绿片岩的蠕变损伤本构关系。
但是前人研究和改进工作主要集中在对流变过程中加速流变的改进和模拟,而对于加载初期产生的瞬时变形没有过多的研究。李娜等[9]通过对深部岩石进行分级增量循环加卸载蠕变试验,表明该岩石试件抵抗瞬时塑性变形的能力随着应力水平的提高而增强。刘栋等[10]对粉砂岩进行了单体分级增量循环加卸载流变试验,试验表明随着应力循环的增加,该岩样材料抵抗瞬塑性变形的能力逐渐增强。程龙等[11]对红砂岩进行了分级增量循环加载流变试验,探讨了围压、水压对红砂岩瞬时变形、蠕变变形、长期强度以及破坏荷载的影响规律。杨圣奇[12]通过不同尺寸的岩石单轴压缩试验指出,不同尺寸岩样的变形模量由于受加载初期非线性变形的影响,表明了加载初期非线性变形部分的重要性。赵延林等[13]通过对软弱节理矿岩进行蠕变试验,按瞬时弹性应变、黏弹性应变、瞬时塑性应变与黏塑性应变对流变试验数据进行分析,探讨了软弱节理矿岩的黏弹塑性变形特性。
综上所述,前人对分级增量循环加卸载蠕变试验数据中的瞬时塑性应变的研究不多,在模型参数识别过程中没有考虑瞬塑应变值的大小[14-15],特别是在卸载条件下,这将给模型参数的计算带来误差,因此将瞬塑应变从瞬时应变中辨识以及分离出来,并采用合理的数值模型进行描述,同时与传统流变模型相结合建立改进模型来描述岩石流变试验结果,对提高岩石物理参数的精确度和准确性有意义。
1 岩石流变模型的建立
1.1 瞬时塑性元件
通过观察岩石的应力-应变曲线可以发现,在加载初期,应力-应变曲线在加载初期呈上凹形,这是由于在加载过程中岩体内部的结构调整、结构面在受压过程中产生闭合、滑移与错动造成的[9-10]。同时,由于软岩材料内部存在大量的微观裂隙和孔隙,故在其受力变形的瞬间会存在一微观裂隙的有限压密闭合阶段,由此表现出随应力增加其应变增长率减小的瞬时塑性,随着岩石中微裂隙的不断闭合,其抵抗该瞬时塑性变形的能力(刚度)将会不断增强[9]。
在岩石流变中采用模型元件来模拟这种因裂隙闭合效应而产生的变形,以往的研究还没有很好解决。本文在此引入一种裂隙塑性体元件。如图1所示,该裂隙塑性元件所受应力随应变的变化率与应变的大小成正比,即

式中,k1为比例系数;k2为应力初始值,MPa;σ为应力,MPa;ε为应变。

图1 岩石裂隙塑性体Fig.1 Crack plasticity of rocks
当该裂隙塑性元件的应变为0时,其所受的应力也应该为0,即当ε=0时,有σ=0。根据这一初值条件,将式(1)积分可以得到

1.2 岩石流变模型的建立
将虎克模型(H)、圣维南模型(S)和牛顿模型(N)与本文提出的裂隙塑性元件(E)按如图2所示的方式连接成改进的Burgers模型。其中,H体模拟瞬时弹性;E体模拟瞬时塑性;H/N体模拟黏弹性;N体模拟黏塑性。该模型的力学参数见表1。
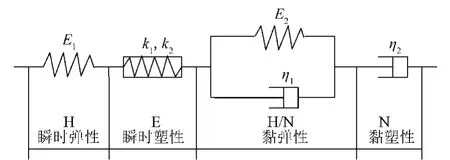
图2 改进的Burgers流变模型Fig.2 Modified Burgers model of rocks
该模型能反映岩石流变过程中表现出的瞬时弹性、瞬时塑性、黏弹性和黏塑性,由改进模型的组合特征可以得到,其应力-应变关系为

表1 改进的Burgers模型的力学参数Table 1 Parameters of modified Burgers model

式中,σ1,σ2,σ3,σ4分别为图2所示模型中4部分所受应力;ε1,ε2,ε3,ε4分别为模型中4部分在压应力作用下的轴向应变。
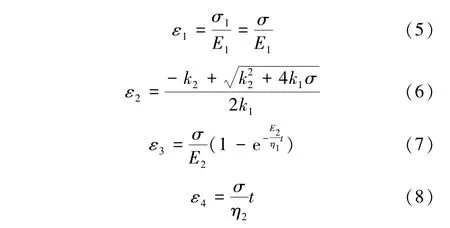
由此得到改进Burgers模型的本构方程为

式中,η1,η2为牛顿体黏性系数;E1,E2为虎克体弹性系数。
该流变状态方程在蠕变和恒加载速率情况下比较简单,而对于松弛和恒应变速率情况却相对复杂。为了进一步认识该复合力学模型,下面对其加卸载蠕变力学特性进行一些讨论。
模型受恒定偏应力σ0作用下时发生蠕变,其应变值会随着时间逐渐增大,由流变方程得其加载蠕变方程为

通过研究模型本构方程,可以发现此模型具有瞬时弹性、瞬时塑性、黏弹性和黏塑性,相应的模型具有瞬时弹性应变、瞬时塑性应变、衰减蠕变以及等速蠕变,蠕变速率随时间逐渐减小最终趋于某一恒定值。这反映了过渡蠕变阶段的特性。观察式(10),(12)可以看出,改进的Burgers模型与传统的Burgers模型的蠕变方程形式完全相同,但2种模型表示的瞬时弹性应变、瞬时塑性应变以及等速蠕变值差别较大。
1.3 改进的Burgers流变模型参数的确定
改进的Burgers模型中总应变由瞬时弹性应变εme、瞬时塑性应变εmp、黏弹性应变εce和黏塑性应变εcp四部分组成,如图3所示。

图3 黏弹塑应变分离示意Fig.3 Separation of viscoelastic plasticity strain
将流变试验数据中应变量分离成瞬时应变分量(试验曲线部分斜率较大的初始阶段)和蠕变应变分量(试验曲线斜率逐渐减小并最终趋于稳定)2部分。通过试验获得试样在不同应力水平下的加卸载蠕变试验数据,分离出试验数据中εme,εmp,εce以及εcp。可以很方便的求解出各元件的力学参数。具体步骤如下:
(1)对于虎克体,利用试验所得的各应力水平σi作用下的瞬弹性应变εmei,取其中的某一应力σi对应的应变εmei,据公式εmei=σi/E1。可计算得到虎克体的力学参数E1i,对多组试验数据得到的E1i进行数据处理,最后求均值得到最终虎克体参数E1。
(2)对于裂隙塑性体,利用试验所得的各应力水平σi作用下的瞬塑性应变εmpi,取其中的任意2组数据(σi,εmpi),(σj,εmpj),代入裂隙塑性体的本构方程即可解得其力学参数k1,k2。

(3)对于开尔文体,根据各低应力σi水平作用下的黏弹性应变稳定值,可解得参数E2。选取某一时刻t1在应力水平σi作用下的εcei,可解得参数η1,所用公式为

(4)对于牛顿体,从式(10),(11)可以看出,在加载条件下,岩石蠕变速率逐渐减小,最终趋于稳定值,岩石流变函数在加载后期趋于一个线性函数。选取某一应力水平σ0加载条件下的流变试验曲线的后期线性部分,采用线性函数y=kx+b进行拟合,得到直线段斜率k和截距b的拟合值,其中k=σ0/η2。由此可以得到黏塑性部分的参数η2拟合值。
至此,改进的Burgers流变模型的所有力学参数全部解出。
2 模型的验证
为了验证本文提出的裂隙塑性体以及改进的Burgers模型的正确性与合理性,基于莒山矿粉砂岩不同围压下瞬时全应力-应变曲线和单体分级加卸载流变试验结果,对本文提出的裂隙塑性体和改进流变模型进行验证和分析。
2.1 不同围压下粉砂岩全应力-应变分析
岩石瞬时力学性质试验方案的荷载设计可以按照等差序列进行设计,也可以按照等比序列进行设计,为了能通过有限个试样的力学试验,全面反映粉砂岩在不同围压下的力学性质,试验设计围压水平分别为0,5,15及25 MPa,获得了粉砂岩在不同围压下的应力-应变曲线,如图4所示。由图4应力应变曲线可以看出,不同围压作用下粉砂岩应力-应变曲线都出现了裂隙压密阶段和弹性变形阶段。
裂隙压密阶段粉砂岩应力-应变曲线出现明显的上凹段,该阶段应力-应变曲线的斜率不断增大。这主要是由于粉砂岩试样内部分布着大量的裂隙、孔洞等天然缺陷,在外荷载的作用下试样内部缺陷不断地挤压密实。随着试样中原生裂隙等的逐渐压密,试样整体刚度不断增大,试样轴向变形减缓,应力-应变曲线斜率增大。

图4 不同围压下粉砂岩应力-应变曲线Fig.4 Stress-strain curves of siltstone under different confining pressures
根据不同围压下粉砂岩试样瞬时力学性质试验结果,分析粉砂岩强度特性,围压为0时试样的峰值强度为133.51 MPa,围压增加到5,15,25 MPa时,峰值强度分别为157.87,181.16,205.24 MPa。粉砂岩试样峰值强度随围压的提高而提高,围压对粉砂岩的峰值强度有强化作用。将粉砂岩峰值强度与围压关系绘制于图5中,并根据粉砂岩试样试验数据拟合出围压与峰值强度的关系式:σ′1=3.75σ′3+138.55,其相关系数R2=0.99,峰值强度与围压水平呈较好的线性关系,符合摩尔-库伦准则。

图5 峰值强度与围压的关系Fig.5 Relationship between peak strength and confining pressure
将摩尔-库伦准则以主应力的形式表示,如式(16)所示。
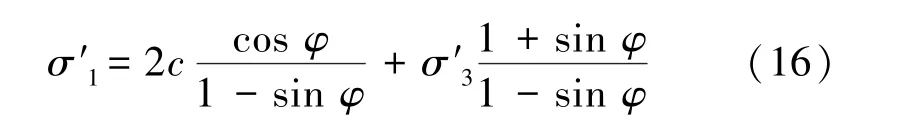
其中,c为黏聚力;φ为内摩擦角。将围压和峰值强度的拟合关系式代入式(16)中可以求得粉砂岩试样黏聚力c=35.8 MPa,内摩擦角φ=35.4°。
2.2 粉砂岩试样蠕变变形规律
采用多级增量循环加卸载方式,获得了不同围压下红砂岩试样加卸载流变试验曲线,这里取围压为10 MPa,应力水平分别为120,140,163和168 MPa条件下试样的加卸载流变试验结果进行分析,对试验数据进行简单处理后得到的蠕变曲线如图6所示。
(1)瞬时变形性质。

图6 不同荷载下粉砂岩加卸载流变试验曲线Fig.6 Creep strains under different loading conditions
基于围压为10 MPa条件下粉砂岩试样蠕变试验结果,对试验数据进行整理和分析,辨识出每一级荷载作用下试件的瞬时应变εm、加载最终稳定应变ε∞1、黏弹性回复点ε1和最终塑性应变εp,根据这些已知量间接求出瞬时弹性应变εme、瞬时塑性应变εmp、黏弹性应变εce和黏塑性应变εcp,见表2。
从表2中数据可以看出,该粉砂岩的瞬时应变由瞬时弹性应变和瞬时塑性应变组成,其中瞬时弹性应变占主要部分,但瞬时塑性应变所占比例超过了20%,因此在模型参数计算中不能忽略。

表2 黏弹塑应变共存特性试验数据Table 2 Visco-elastic-plastic strain measured data
在加载过程中,分析瞬时弹性应变与轴向应力的关系,结果如图7所示。从图像上看,瞬时弹性应变与应力水平高度线性相关,采用线性关系拟合试验结果,得到瞬时弹性应变与应力水平的关系为:σ= 28.89×103εme,拟合相关性系数R2=0.99。这表明该试样在不同应力水平下其瞬时弹性应变与应力水平成高度线性关系,瞬时弹性模量并未随着应力水平的变化而变化,即E1可以取为28.89 GPa。

图7 瞬时弹性应变与应力水平的关系曲线Fig.7 Stress-instantaneous elastic strain curve
分析瞬时塑性应变与应力水平的关系,并采用本文提出的瞬时塑性元件进行拟合,结果如图8所示。得到瞬时塑性应变与应力水平之间的关系式为:σ=参数拟合相关系数达到了0.9。从关系曲线可以看到,试验值与本文提出的裂隙塑性体元件拟合较好,证明了本文提出的裂隙塑性体对于描述该种岩石的瞬时塑性应变是正确合理的。
观察粉砂岩加卸载流变试验曲线,在本试验中,蠕变部分都出现了衰减蠕变分量和稳定蠕变分量,但稳定蠕变分量很小,从表2黏弹塑应变共存特性试验数据中也可以看出,由于黏塑性应变分量十分小,表中应变值会受到取值精度的影响。试验表明试样的黏塑应变值远小于瞬塑应变值,因此在该粉砂岩流变过程中,可以认为塑性应变值主要由瞬塑应变构成,瞬塑应变值的忽略将会给黏塑性元件参数η2的计算带来较大误差。
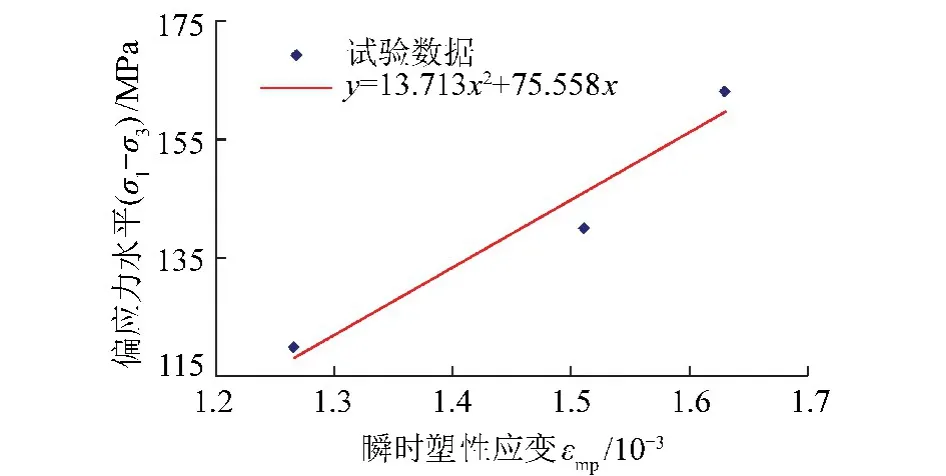
图8 瞬时塑性应变与轴向应力关系曲线Fig.8 Stress-instantaneous plasticity strain curve
(2)黏性变形性质。
基于对围压为10 MPa、不同应力水平下粉砂岩流变试验结果进行整理分析(表2),观察试样试验蠕变曲线(图6),可以认为粉砂岩的流变特性与改进的Burgers模型较为吻合,这里采用改进的Burgers模型来描述粉砂岩的流变特性。瞬时变形部分参数前文已经求出,黏性蠕变部分参数可以按照式(10)拟合得到,模型拟合参数见表3,参数拟合的相关性系数都达到了0.9,拟合得到的模型蠕变方程如下所示。
①应力水平为120 MPa时,拟合流变方程为加载条件下:

表3 围压10 MPa下改进Burgers模型拟合结果Table 3 Fitting result of modified Burgers model at a confining pressure of 10 MPa
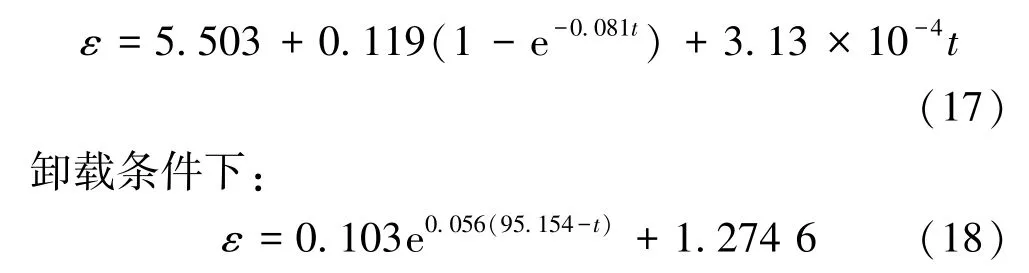
②应力水平为140 MPa时,拟合流变方程为加载条件下:

③应力水平为163 MPa时,拟合流变方程为加载条件下:
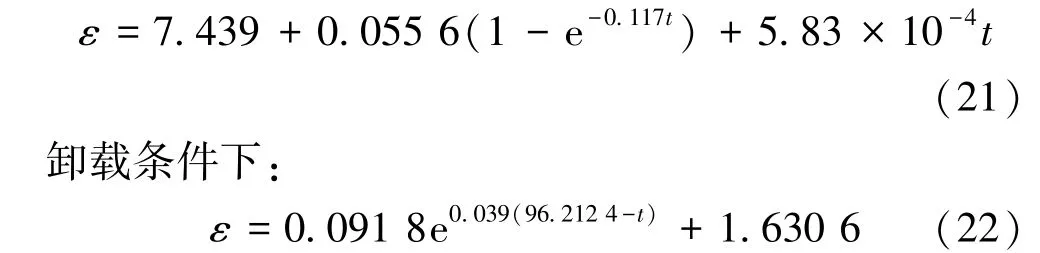
图9给出了围压为10 MPa、应力水平分别为120 MPa和140 MPa下粉砂岩试样加载流变试验结果与改进流变模型拟合结果的对比,从图中可以看出,改进的Burgers模型与试验结果吻合较好。
根据使用试样的加载流变试验数据拟合得到的加载蠕变方程,可以求解出模型的卸载蠕变方程,根据方程画出卸载流变理论曲线,将模型理论曲线与卸载流变试验数据进行对比。图10给出了围压为10 MPa、应力水平分别为120 MPa和140 MPa下粉砂岩试样卸载流变试验结果改进的Burgers模型拟合结果的对比,从图中可以看出,改进的Burgers模型能较好的描述粉砂岩的流变特性,包括加载状态和卸载状态。
(3)与传统Burgers模型的对比。
采用传统的Burgers模型对围压为10 MPa、应力水平分别为120,140和163 MPa下粉砂岩试样加载流变试验结果进行描述,其结果与改进流变模型拟合结果完全相同,蠕变方程见式(17),(19)和(21)。这是由于改进的Burgers模型与传统Burgers模型相比并未改变总的瞬时变形和黏性变形值,因此在加载条件下二者的拟合方程和拟合曲线完全相同。

图9 围压10 MPa加载条件下改进Burgers模型拟合结果Fig.9 Fitting results of modified Burgers model at a confining pressure of 10 MPa on load condition
根据在加载条件下得到的流变方程,可以按照式(12)求解出卸载条件下相应的蠕变方程,将式(12)改写为ε=aexp[b(c-t)]+d的方程形式,通过加载模型,计算得到传统Burgers模型与改进模型的卸载蠕变方程系数见表4。
分析式(17)~(22),当应力水平分别为120,140以及163 MPa时,试样的塑性应变值(×103)分别近似为1.274 6,1.431 7和1.630 6,采用传统Burgers模型的蠕变方程(式(12))计算所得的塑性应变值(×103)分别为0.029 8,0.015 7和0.054 9,而采用改进的Burgers模型的蠕变方程计算所得的塑性应变值(×103)分别为1.378 8,1.529 7和1.955 7。传统Burgers模型计算出来的塑性应变值与试验结果差别较大,这是由于传统的Burgers模型没有将瞬时塑性应变值分离出来,使得模型的卸载方程中塑性应变计算值与试验结果差别较大,但在改进的Burgers模型中,模型的瞬时应变被分为了瞬时弹性应变和瞬时塑性应变2部分,能较好的描述试样的瞬时变形特性,使得改进模型的塑性应变值与试验值差别较小,较为吻合。

图10 围压10 MPa卸载条件下模型拟合结果Fig.10 Fitting results of model at a confining pressure of 10 MPa on unload condition

表4 卸载条件下模型计算结果与试验结果Table 4 Comparison of the calculated results and the tests result at a confining pressure of 10 MPa on unload condition
将传统Burgers模型的卸载方程曲线与卸载试验曲线以及改进的Burgers模型卸载曲线进行对比。图10也给出了围压为10 MPa、应力水平分别为120 MPa和140 MPa条件下粉砂岩试样卸载流变试验与模型模拟的结果对比。
对比模型拟合曲线与试验曲线(图10)可以看出,与改进的Burgers模型卸载曲线相比,传统的Burgers模型的卸载曲线与试验卸载曲线差别较大。
3 结 论
(1)岩石的瞬时塑性变形是在岩石蠕变过程中(尤其是软岩)普遍存在的现象,且随应力水平的增高,瞬时塑性应变增大,不同岩石流变试验中瞬时塑性应变的大小并不同,在某些岩石流变试验中其大小不容忽视。
(2)提出了一种用于描述瞬时塑性应变的裂隙塑性体,并将该元件与传统的Burgers模型结合,构成改进的Burgers流变模型,给出了该模型加卸载流变方程,并对该模型的蠕变特性进行了分析,给出了模型参数确定方法。该模型能描述岩石在不同应力水平下的衰减蠕变和稳态蠕变。
(3)选取莒山矿粉砂岩的试验结果对本文提出的模型进行验证。对该粉砂岩试样进行瞬时三轴压缩试验,得到了该试样的全应力-应变曲线,以及峰值强度与围压之间的线性关系式。采用改进的Burgers模型对不同应力水平下的流变试验曲线进行描述,效果较好。采用传统Burgers模型对试验曲线进行描述,加载条件下的蠕变方程与改进的Burgers模型完全相同,在卸载条件下与试验曲线差别较大,而改进的Burgers模型卸载方程与试验曲线相似性较高,验证了模型的正确性和合理性。
[1] 周维垣.高等岩石力学[M].北京:水利电力出版社,1990:173-174.
Zhou Weiyuan.Advanced rock mechanics[M].Beijing:Water Resources and Electric Power Press,1990:173-174.
[2] 蔡美峰,何满潮,刘东燕.岩石力学与工程[M].北京:科学出版社,2009:198-219.
Cai Meifeng,He Manchao,Liu Dongyan.Rock mechanics and engineering[M].Beijing:Science Press,2009:198-219.
[3] 孙 钧.岩土材料流变及其工程应用[M].北京:中国建筑工业出版社,1999.
Sun Jun.Rheological behavior of geometrical and its engineering applications[M].Beijing:China Architecture and Building Press, 1999.
[4] 夏才初,王晓东,许崇帮,等.用统一流变力学模型理论辨识流变模型的方法和实例[J].岩石力学与工程学报,2008,27(8): 1594-1600.
Xia Caichu,Wang Xiaodong,Xu Chongbang,et al.Method to identify rheological models by unified rheological model theory and case study[J].Chinese Journal of Rock Mechanics and Engineering,2008, 27(8):1594-1600.
[5] 夏才初,王晓东,许崇帮,等.统一流变力学模型参数的确定方法[J].岩石力学与工程学报,2009,28(2):425-431.
Xia Caichu,Wang Xiaodong,Xu Chongbang,et al.Method for parameters determination with unified rheological mechanical model[J].Chinese Journal of Rock Mechanics and Engineering,2009, 28(2):425-431.
[6] 杨圣奇,徐卫亚,杨松林.龙滩水电站泥板岩剪切流变力学特性研究[J].岩土力学,2007,28(5):895-902.
Yang Shengqi,Xu Weiya,Yang Songlin.Investigation on shear rheological mechanical properties of shale in Longtan hydropower project [J].Rock and Soil Mechanics,2007,28(5):895-902.
[7] 邓荣贵,周德培,张倬元,等.一种新的岩石流变模型[J].岩石力学与工程学报,2001,20(6):780-784.
Deng Ronggui,Zhou Depei,Zhang Zhuoyuan,et al.A new rheological model for rocks[J].Chinese Journal of Rock Mechanics and Engineering,2001,20(6):780-784.
[8] 徐卫亚,周家文,杨圣奇,等.绿片岩蠕变损伤本构关系研究[J].岩石力学与工程学报,2006,25(S1):3093-3097.
Xu Weiya,Zhou Jiawen,Yang Shengqi,et al.Study on creep damage constitutive relation of green schist specimen[J].Chinese Journal of Rock Mechanics and Engineering,2006,25(S1):3093-3097.
[9] 李 娜,曹 平,衣永亮,等.分级加卸载下深部岩石流变试验及模型[J].中南大学学报(自然科学版),2011,42(11):3465-3471.
Li Na,Cao Ping,Yi Yongliang,et al.Creep properties experiment and model of deep rock with step loading and unloading[J].Journal of Central South University(Science and Technology),2011, 42(11):3465-3471.
[10] 刘 栋.深部围岩蠕变特性试验研究[D].长沙:湖南科技大学,2011:45-70.
Liu Dong.Experimental study on creep characteristics of deep surrounding-rock[D].Changsha:Hunan University of Science and Technology,2011:45-70.
[11] 程 龙.高围压高水压下红砂岩流变力学特性试验与模型研究[D].徐州:中国矿业大学,2013.
Cheng Long.Experiment and model study on rheological mechanical behavior of red sandstone under high confining pressure and hydraulic pressure[D].Xuzhou:China University of Mining and Technology,2013.
[12] 杨圣奇.裂隙岩石力学特性研究及时间效应分析[M].北京:科学出版社,2011:33-36.
Yang Shengqi.Fractured rock mechanics characteristics research and time effect analysis[M].Beijing:Science Press,2011:33-36.
[13] 赵延林,曹 平,陈阮江,等.分级加卸载下节理软岩流变试验机模型[J].煤炭学报,2008,33(7):748-753.
Zhao Yanlin,Cao Ping,Chen Ruanjiang,et al.Creep properties experiment and model of jointed soft rocks under step load and unload [J].Journal of China Coal Society,2008,33(7):748-753.
[14] 王永岩,李剑光,魏 佳,等.黏弹性有限元反分析方法及其在软岩流变问题中的应用[J].煤炭学报,2007,32(11):1162-1165.
Wang Yongyan,Li Jianguang,Wei Jia,et al.Viscoelastic finite element back analysis method and its application in problem of soft rock rheology[J].Journal of China Coal Society,2007,32(11): 1162-1165.
[15] 李栋伟,汪仁和,范菊红,等.软岩屈服面流变本构模型及围岩稳定性分析[J].煤炭学报,2010,35(10):1604-1608.
Li Dongwei,Wang Renhe,Fan Juhong,et al.Yield surface constitutive creep model and stability analysis of soft rock roadway[J].Journal of China Coal Society,2010,35(10):1604-1608.
Modified Burgers model of rocks and its experimental verification
XU Peng,YANG Sheng-qi,CHEN Guo-fei
(State Key Laboratory for Geomechanics and Deep Underground Engineering,China University of Mining and Technology,Xuzhou 221008,China)
To describe the change law of instantaneous plasticity strain under different axial stresses,a new crack plasticity component was put forward based on the previous study results on instantaneous plasticity strain in rheological experiments of rocks.Combining this component with the classic Burgers model to constitute an improved rheological model,the load-unload rheological equations of the improved model were given.In this paper,the creep property of the model was analyzed,and the method for parameters determination with improved Burgers model was introduced.The instantaneous experiment on siltstone in Jushan Mine under different confining pressures were carried out,the stressstrain curves of siltstone under different confining pressures and the relationship between axial strength and confining pressure were obtained.Considering the load-unload creep experimental data of siltstone in Jushan Mine under different stress levels,the instantaneous plasticity strain cannot be ignored.The modified Burgers can effectively describe the creep properties of the siltstone under different stress levels.The study demonstrates the validity and rationality of the improved Burgers rheological model by comparing the traditional Burgers model with the test results.
modified Burgers model of rocks;instantaneous plasticity strain;crack plasticity component
TD313
A
0253-9993(2014)10-1993-08
2013-09-16 责任编辑:王婉洁
国家重点基础研究发展计划(973)资助项目(2014CB046905);国家自然科学基金资助项目(41272344);江苏省自然科学基金面上资助项目(BK2012568)
徐 鹏(1992—),男,湖北荆州人,硕士研究生。E-mail:2009301550146@whu.edu.cn。通讯作者:杨圣奇(1978—),男,教授,博士生导师,博士后。E-mail:yangsqi@hotmail.com
徐 鹏,杨圣奇,陈国飞.改进的岩石Burgers流变模型及其试验验证[J].煤炭学报,2014,39(10):1993-2000.
10.13225/j.cnki.jccs.2013.1337
Xu Peng,Yang Shengqi,Chen Guofei.Modified Burgers model of rocks and its experimental verification[J].Journal of China Coal Society, 2014,39(10):1993-2000.doi:10.13225/j.cnki.jccs.2013.1337

