高地应力断层破碎带衬砌力学特性对比与分析

刘 凯,孔 超,唐浚哲,徐雨平

(西南交通大学交通隧道工程教育部重点实验室,土木工程学院,成都 610031)

高地应力断层破碎带衬砌力学特性对比与分析

刘 凯,孔 超,唐浚哲,徐雨平

(西南交通大学交通隧道工程教育部重点实验室,土木工程学院,成都 610031)

以高地应力区某穿越断层破碎带隧道为工程依托,通过三维数值模拟来分析随着掌子面推进过程中的围岩空间应力场的状态及其变化趋势。首先,根据弹性衬砌模型计算结果判断衬砌结构是否还处于弹性状态;其次,按照弹塑性衬砌模型进行某穿越高地应力断层破碎带隧道三维数值模拟。计算结果表明:高地应力区穿越断层破碎带隧道三维数值模拟应该采用弹塑性衬砌结构;弹性计算模型与摩尔—伦计算模型分别计算所得衬砌结构关键点位移量差别较大,弹性衬砌模型计算得到关键点位移均小于摩尔—库伦衬砌模型所得到的量值,且约为摩尔—库伦模型计算所得量值的50%;拱顶和拱腰主应力波动范围在掌子面通过z=-50 m平面前0.5B(B为隧道宽度)和通过后1.5B范围,墙脚主应力波动范围在掌子面通过前1B和通过后0.5B范围;弹塑性衬砌计算的主应力较弹性衬砌计算的主应力大;揭示了某穿越高地应力断层破碎带隧道衬砌的破坏形式与潜在破坏面。

隧道;高地应力;断层;围岩;弹性;弹塑性;摩尔-库伦准则;三维数值模拟

高地应力条件下进行隧道开挖一直是困扰当今隧道建设的难题之一[1,2]。加之隧道开挖中又遇到软弱断层带,对于隧道建设来说无疑更是难上加难。目前,广大学者针对于此类问题的研究还是比较少,主要运用数值模拟、室内模型试验或者现场经验来指导隧道的设计与施工。

在高地应力、软弱断层带条件下,三维数值模拟大多将衬砌结构视为弹性模型来处理。然而,在高地应力、软弱破碎带条件下,由于围岩受到很大的应力作用,再加上软弱破碎带不利影响,衬砌结构会产生较大的变形,如果将衬砌以弹性模型进行处理,往往是不合理的。根据数值模拟计算发现,将混凝土视为弹性和把混凝土视为弹塑性材料进行计算,其结果差别甚大。计算结果表明,高地应力、软弱断层带隧道衬砌结构应采用弹塑性模型进行计算。

由于高地应力区以及断层破碎带是隧道施工中常见不良地质条件,极易出现塌方、大变形、突水突泥等工程事故,给施工带来重大损失。因此,开展针对此不良地质的隧道施工力学、围岩破坏规律以及围岩稳定性研究,以及隧道穿越此不良地质条件引起的三维应力场重分布就显得尤为重要。本文以国内某穿越高地应力软弱断层带的隧道为例进行计算与分析。

1 三维数值建模

围岩级别为Ⅰ级,穿越断层破碎带,带宽为15 m,其走向垂直于隧道轴线方向,倾角为75°,具体物理力学参数如表1所示。隧道埋深为500 m,最大水平应力为23.35 MPa,属于高地应力区。采用上下台阶法施工,开挖进尺C为5 m,台阶长度L为5 m,上下台阶初支均落后于上下掌子面5 m。例如,第10施工步时,上台阶掌子面开挖到z=-50 m,下台阶到z= -45 m。隧道宽度为10.3 m,高度H为8 m。开挖断面面积为66.47 m2。初支混凝土厚度为0.2 m,采用C35喷射混凝土进行支护,钢筋混凝土配筋率为6.0%。计算模型采用应力边界条件,根据表2所示应力数据,沿着隧道轴线和垂直于隧道轴线的水平地应力通过测压力系数Kz=1.54和Kx=1.38施加在模型边界上。

表1 材料物理力学参数

表2 初始地应力MPa

本文采用有限差分软件FLAC3D进行模拟计算,拟采用摩尔-库伦准则,计算模型三维尺寸为x×y×z: 110 m×90 m×100 m,如图1所示。

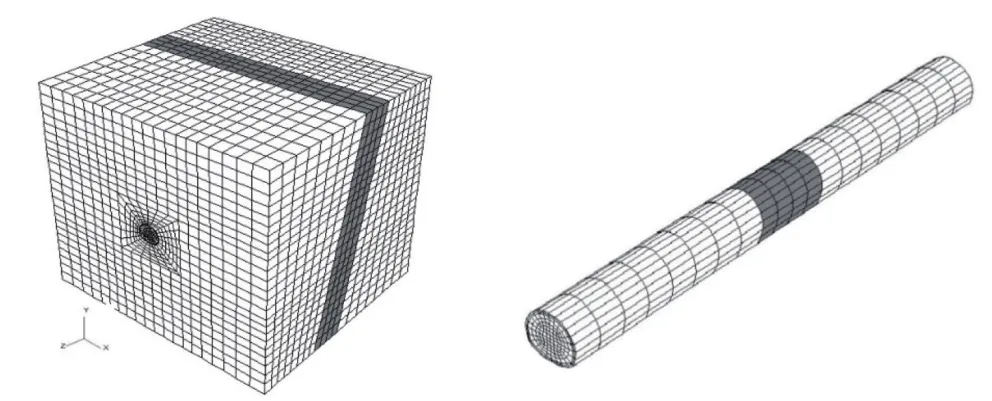
图1 三维模型

2 弹性本构模型与摩尔-库伦准则选用

高地应力条件下,隧道穿越断层破碎带往往伴随围岩发生塑性变形,因而对于围岩,计算应采用摩尔-库伦本构模型;钢筋混凝土衬砌,同样会因为高地应力和相对较软弱的断层而产生较大的变形。因此,进行穿越高地应力断层破碎带的隧道模型计算时,对隧道衬砌采用弹性模型往往是不合理的,应该采用摩尔-库伦准则进行计算。

2.1 假定弹性计算

计算模型假设为弹性来计算,结果显示:衬砌结构上每个混凝土条的应变已经超过了混凝土的极限压应变。其中,将每个条带简化为一根直杆来计算其产生的应变,如图2所示。表3列出衬砌断面(z=-50)在弹性模型下时衬砌各个单元的应变值。

图2 衬砌结构分段与受力变形

表3 衬砌结构应变10-3

混凝土发生屈服需满足如下方程

其中,[ε]为混凝土极限应变。

当混凝土应变满足方程(1)时,混凝土发生屈服,混凝土已经由弹性进入到塑性阶段。从表3可以看出,杆件1～24的应变值均大于混凝土极限压应变值0.002。因此,衬砌假定为弹性来计算是不合理的,应采用弹塑性本构模型进行计算。

2.2 衬砌结构等效模型参数[3]

结合文献[3]针对沉管衬砌受力特点,对钢筋混凝土材料进行等效计算,推导出深埋隧道钢筋混凝土结构受力特点的公式。

2.2.1 等效抗剪强度指标c、φ值

假设钢筋混凝土截面总面积为A,混凝土截面面积为AC,钢筋截面面积为AS。混凝土截面处于剪力S的作用下时,剪力S由混凝土产生的抗力SC与钢筋产生的抗力共同来承担,有

其中,SC为混凝土承担的剪力;SS为钢筋承担的剪力。

由材料的摩尔-库伦强度准则

对于混凝土有

式中,AC为受力混凝土截面面积;τC为混凝土截面所受的剪应力;φC为混凝土材料的摩擦角;cC为混凝土材料的黏聚力。

由上式可得,混凝土应变为

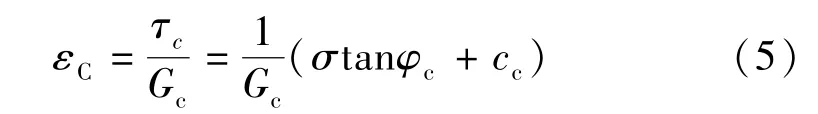
式中,εc为混凝土材料的剪切应变;Gc为混凝土剪切模量。

根据钢筋混凝土材料变形协调原则,钢筋剪应变与混凝土剪应变相等,有

式中,εs为钢筋的剪切应变。

因此,钢筋承担的剪力Ss为

式中,Gs为钢筋剪切模量;As为钢筋截面面积。

对于混凝土材料等效模型,等效摩擦角φc以及等效黏聚力ce与等效材料所承受的剪力的关系表示如下

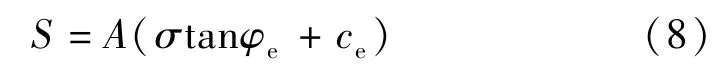
由式(7)结合式(2)、(4)、(7)可得,混凝土材料的等效摩擦角φe以及等效黏聚力ce为

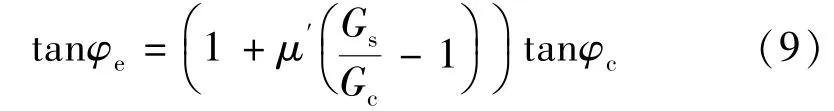
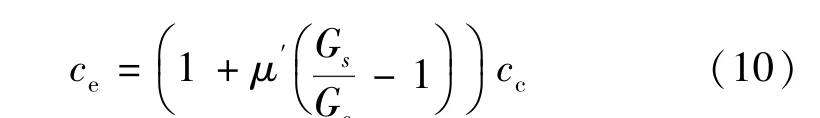
其中,μ′为钢筋配筋率。

2.2.2 混凝土材料等效抗拉强度指标

(1)混凝土和钢筋共同承担荷载阶段

混凝土在此阶段由弹性阶段一直到裂缝贯穿截面为止。混凝土的抗拉强度较小,当钢筋混凝土处于受拉状态时,如果屈服也是混凝土材料先达到屈服强度。假定钢筋和混凝土材料变形协调,混凝土屈服时的应变为

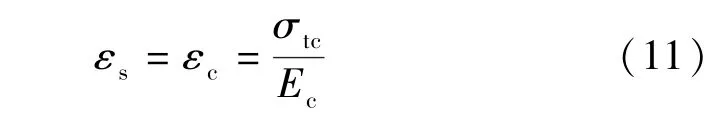
式中,σtc为混凝土的抗拉强度;Ec为混凝土的弹性模量。

因此,混凝土和钢筋中的拉应力分别为

其中,Es为钢筋的弹性模量。

假设钢筋混凝土截面总面积为A,混凝土截面面积为Ac,钢筋截面面积为As,钢筋混凝土等效模型的抗拉强度为σt。混凝土截面处于拉力T的作用下时,拉力T由混凝土产生的抗力Tc与钢筋产生的抗力Ts共同来平衡,有

将式(12)、式(13)代入式(14)有

(2)混凝土退出工作,钢筋承担全部荷载

混凝土已经屈服退出了工作,钢筋混凝土截面产生的拉力T全由钢筋来承担,即式(14)中的Tc=0。此时,式(14)有

式中,σts为钢筋的抗拉强度。

3 衬砌弹性、弹塑性影响与分析

3.1 位移分析

拱顶沉降随施工步变化如图3所示。弹性模型计算表明,对于拱顶沉降,最终沉降值为17.20 mm;最大位移量发生在由第10施工步向第12施工步开挖时,为11.85 mm,约占最终沉降量的68.9%;在开挖至第10施工步时,发生位移量为1.02 mm,约占最终沉降量的5.9%;第12施工步至最后一个施工步,发生位移为2.00 mm,约占最终沉降量的11.6%。当采用摩尔-库伦模型计算时,最终沉降值为42.40 mm;最大位移量发生在由第10施工步向第11施工步开挖时,为30.62 mm,约占最终沉降量的72.2%;在开挖至第10施工步时,发生位移量为4.88 mm,约占最终沉降量的11.5%;第11施工步至最后一个施工步,发生位移为3.70 mm,约占最终沉降量的16.3%。由弹性模型与摩尔-库伦本构模型计算表明,弹性模型的最终沉降量始终小于摩尔-库伦模型计算所得最终沉降量,约为摩尔-库伦模型计算的40%。

仰拱隆起随施工步变化如图3所示。采用弹性模型得到的最终隆起量为6.12 mm;在第8施工步向第12施工步推进时,仰拱隆起快速地由0.44 mm增长到4.95 mm,占最终沉降量的73.7%;第12施工步向后推进,隆起量从4.95 mm缓慢增长到6.12 mm,占最终沉降量的19.1%。采用弹塑性衬砌模型得到的最终隆起量为20.70 mm;在第8施工步向第12施工步推进时,仰拱隆起快速地由0.40 mm增长到20.88 mm,占最终沉降量的98.9%;之后以小于0.7 mm波动,说明仰拱隆起已经基本完成。由弹性模型与摩尔-库伦本构模型计算表明,弹性模型的最终隆起量始终小于摩尔-库伦模型计算所得最终值,约为摩尔-库伦模型计算的30%。

净空收敛计算结果随施工步变化如图4所示。当衬砌采用弹性模型计算时,净空收敛的最终值为49.40 mm;在第8施工步时,净空收敛为1.29 mm,约占最终值的2.6%;在第13步时,净空收敛达到49.30 mm,约占最终沉降值的100%,此后一直以小于4 mm在波动,说明在第13施工步时,净空收敛已经完全释放完毕;由第8施工步向第13施工步开挖所引起的净空收敛值为48.01 mm,约占最终沉降的97.2%;施工步影响净空收敛的范围大致为监测点处±1.5B。当衬砌采用弹塑性模型计算时,净空收敛的最终值为97.27 mm;在第8施工步时,净空收敛为1.79 mm,约占最终值的1.8%;在第13步时,净空收敛达到97.27 mm,约占最终沉降值的100%,此后一直以小于3 mm的幅度在波动,说明在第13施工步时,净空收敛已经完全释放完毕;在由第8施工步向第13施工步开挖所引起的净空收敛值为95.48 mm,约占最终沉降的98.2%;施工步影响净空收敛的范围大致为监测点处±1.5B。由弹性模型与摩尔-库伦本构模型计算表明,弹性模型的最终收敛值始终小于摩尔-库伦模型计算所得最终值,约为摩尔-库伦模型计算的50%。

采用弹性模型与弹塑性模型分别计算出地表点S (0,0,-50)的沉降量随施工步变化如图5所示,两条沉降曲线几乎呈线性变化。采用弹性衬砌模型时,地表最终沉降量约为5.43 mm;采用塑性衬砌模型,地表最终沉降量约为10.30 mm。采用弹性衬砌模型所得到的最终沉降量约为摩尔-库伦衬砌模型所得到的最终沉降量的50%。平面z=-50 m上地表关键点编号如图6所示。图7表明衬砌弹性与弹塑性衬砌导致垂直于隧道轴向方向z=-50 m的地表形状的变化趋势与形状。弹性衬砌模型计算得到的地表中心点最大沉降量约为5.43 mm;摩尔-库伦衬砌模型计算得到的地表中心点最大沉降量约为10.30 mm。且两种计算模型计算得到的地表形状均呈现两边高,中间低的态势。且弹性模型计算得到的地表沉降观测点的沉降量值均小于采用摩尔-库伦弹塑性模型得到的观测点的最终沉降量值,弹性模型观测点最终沉降量值约为摩尔-库伦模型相同点最终沉降量值的50%。

图3 拱顶沉降与仰拱隆起

图4 净空收敛

图5 地表沉降

3.2 应力及破坏形态分析

选取隧道轴线方向z=-50 m平面上的拱顶、拱腰、墙脚这3个关键点的主应力作为观测对象。其应力曲线随施工步变化如图8～图10所示。从图中可以看出,当掌子面通过破碎带时,各关键点主应力均有一定的波动,这是由隧道开挖卸荷回弹所致。对于拱顶主应力,当采用弹性和弹塑性衬砌时,波动范围均为掌子面到达前0.5B和掌子面通过后1.5B范围;对于拱腰主应力,当采用弹性和弹塑性衬砌时,拱腰处主应力突变范围均为掌子面到达前0.5B和掌子面通过后1.5B范围;对于墙脚主应力,当采用弹性和弹塑性衬砌时,墙脚处主应力突变范围约为掌子面通过前的1B和掌子面通过后0.5B范围。且由图9～图11可以看出,塑性衬砌中最大主应力比弹性衬砌计算结果的最大主应力要大;塑性衬砌中最小主应力较弹性衬砌计算结果的最大主应力要大。拱顶、拱腰、墙脚处在掌子面通过时的最大和最小主应力变化均较大,由于断层破碎带处岩体强度较低,经历如此较大的应力波动后,容易发生破坏,导致塌方灾害的发生。

对于弹性模型来说,衬砌结构不会产生破坏。但采用摩尔-库伦本构模型计算结果显示,隧道衬砌在高地应力穿越断层破碎带的条件下,进入过塑性区,如图11～图12所示。由图11可以看出,隧道周围岩土体的潜在破坏面呈现一圆形面,破坏形态为拉伸破坏。图12可以看出,衬砌在此应力条件下呈现整体的剪切和拉伸破坏。

图6 地表关键点编号

图7 地表形状

图8 拱顶主应力

图9 拱腰主应力

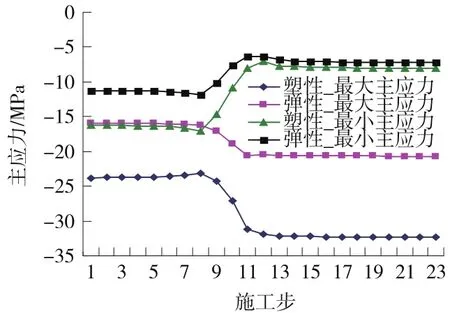
图10 墙脚主应力

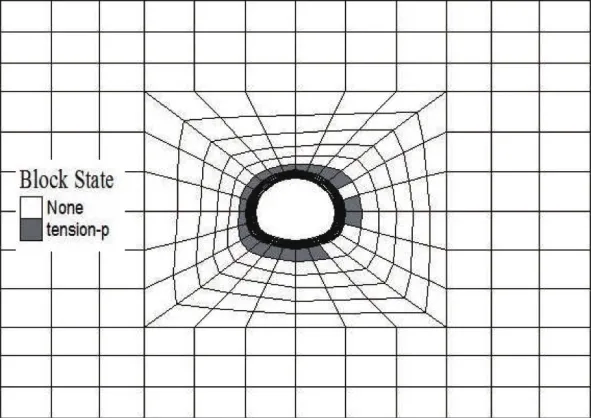
图11 围岩塑性区

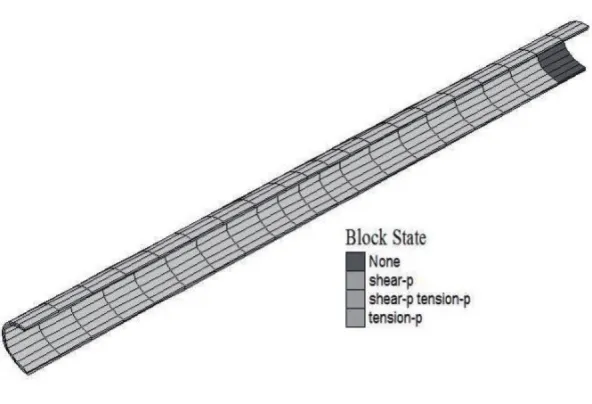
图12 衬砌结构塑性区

断层破碎带的存在不利于围岩的稳定,在隧道开挖过程中,z=-50 m平面上拱顶沉降、仰拱隆起、净空收敛、地表沉降都是先小幅增大后趋于稳定,当掌子面通过时,位移发生突变;弹性衬砌模型计算结果均小于塑性衬砌模型计算结果。对于关键点应力,当掌子面通过破碎带时,各关键点主应力均有一定的波动:对于拱顶和拱腰主应力,当采用弹性和弹塑性衬砌时,波动范围均为掌子面到达前0.5B和掌子面通过后1.5B范围;对于墙脚主应力,当采用弹性和弹塑性衬砌时,墙脚处主应力突变范围约为掌子面达到前1B和掌子面通过后0.5B范围。隧道开挖后,洞周围岩曾进入过拉伸塑性区,其潜在破坏面呈现一圆形面;而衬砌曾进入过拉伸和剪切塑性区,在此应力条件下,衬砌结构呈现整体剪切和拉伸破坏。在断层破碎带地区施工隧道时,可采用三维数值分析方法进行模拟分析,找出易发生塌方区域,提早加强支护,防患于未然。

4 结论

(1)高地应力区隧道穿越软弱断层带条件下进行数值模拟计算,采用弹性衬砌模型是不合理的,应该采用弹塑性衬砌模型计算。

(2)相同条件下,弹性衬砌模型计算得到的监测点位移和应力结果与弹塑性衬砌计算模型得到的结果相差较大:弹性衬砌模型得到的监测点的位移均小于弹塑性模型中对应点的位移,约为弹塑性计算结果的50%。

(3)相同条件下,弹塑性衬砌模型计算得到的主应力几乎全部大于弹性衬砌模型计算所得到的主应力。

(4)计算模型在高地应力穿越软弱断层条件下围岩周围发生张拉破坏,潜在破坏面包围隧道洞周向外扩展。本文的研究对高地应力区隧道穿越断层破碎带的围岩稳定性、数值模拟、制定合理的开挖方案具有一定的工程意义。

[1] 李廷春.毛羽山隧道高地应力软岩大变形施工控制技术[J].现代隧道技术,2011,48(2):59-61.

[2] 张梅,何志军,张民庆,等.高地应力软岩隧道变形控制设计与施工技术[J].现代隧道技术,2012,49(6):13-14.

[3] 李秀地,郑颖人,袁勇,石少卿.沉管海底隧道强度折减法分析探讨[J].岩土工程学报,2013,35(10):1876-1877.

[4] 顾洪源.大断面小净距隧道断面优化及其设计参数研究[J].铁道标准设计,2013(2):85-86.

[5] 郇澜.浅埋隧道施工监测与三维有限元仿真模拟[J].铁道标准设计,2012(1):81-82.

[6] 梁庆国,李德武.对岩土工程有限元强度折减法的几点思考[J].岩土力学,2008,29(11):3053-3056.

[7] 陈志敏.高地应力软岩隧道围岩压力研究和围岩与支护结构相互作用机理分析[D].兰州:兰州交通大学,2012:46-67.

[8] 史克臣.特大断面隧道高地应力条件下变形控制技术研究[J].现代隧道技术,2013,50(5):146-149.

[9] 张优利,刘胜春,梁顺,等.隧道穿越断层破碎带关键技术研究[J].武汉理工大学学报,2013,37(3):529-531.

[10]靳晓光,李晓红.高地应力区深埋隧道三维应力场数值模拟[J].重庆大学学报,2007,30(6):97-101.

[11]佘健,何川.软弱围岩段隧道施工过程中围岩位移的三维弹塑性数值模拟[J].岩石力学与工程学报,2006,25(3):623-629.

[12]李文华,李昊,古银城,等.断层对隧道围岩稳定性影响的有限元分析[J].施工技术,2013,42(7):93-96.

Comparison and Analysis of Mechanical Properties of Lining in Fault Fracture Zone with High Geostress

LIU Kai,KONG Chao,TANG Jun-zhe,XU Yu-ping
(MOE Key Laboratory of Transportation Tunnel Engineering,Southwest Jiaotong University,Chengdu 610031,China)

On the basis of a given tunnel through fault fracture zone with high ground stress,the paper analyzes the spatial distribution of stress field of rock mass by simulation with 3D numerals.First,the lining structure in elastic state is determined based on the calculation results of elastic lining model. Second,lining structure as elastic-plastic one is assumed to simulate the excavation with Finite Difference Software FLAC3D.The results show that elastic-plastic lining structure should be used when a tunnel running through high ground stress and fault fracture zone is simulated;there is a big difference between elastic lining structure and elastic-plastic lining structure when they are applied to simulate the dynamic process of excavation respectively and displacement at the key-points in the elastic model;approximately 50%of key-points displacement in Mohr-Coulomb model is smaller than that in Mohr-Coulomb model; the disturbance range of principal stress at crown and at side is 0.5B(B is the width of tunnel)before z=-50 m(central plane)plane and 1.5B after z=-50 m;the disturbance range of principal stress at side foot is 1B before z=-50 m and 0.5B after z=-50 m;the principal stress of elastic-plastic lining structure is higher than that of elastic lining structure;and the research reveals failure mode and potential failure surface.

Tunnel;High ground stress;Fault fracture zone;Elastic;Elastic-plastic;Mohr-Coulomb; 3D numerical simulation

U451+.4

A

10.13238/j.issn.1004-2954.2014.12.024

1004-2954(2014)12-0099-05

2014-03-11;

2014-04-09

刘 凯(1989—),男,硕士研究生。