基于灰色理论和PSO的牵引供电系统可靠性研究

张庆平,赵 峰,王思华

(兰州交通大学自动化与电气工程学院,兰州 730070)

基于灰色理论和PSO的牵引供电系统可靠性研究

张庆平,赵 峰,王思华

(兰州交通大学自动化与电气工程学院,兰州 730070)

采用灰色GM(1,1)模型预测其相关设备中长期的故障数据,增大建模所需数据样本量,提出以威布尔分布模型为基础,基于粒子群算法的智能拟合方法,建立牵引供电系统各设备可靠性分析的数学模型,所建模型全部通过拟合优度K-S检验,证明该方法十分适合于牵引供电系统设备的可靠性建模。运用BDD算法得到用最小割集表示的牵引变电所和接触网故障树模型,综合得到牵引供电系统整体的可靠性模型,并计算出系统的可靠度和平均使用寿命。最后分析可知接触网的可靠性在很大程度上决定了牵引供电系统整体的可靠性,其分析结果为牵引供电系统以后的维护工作提供了理论依据。

牵引供电系统;可靠性;灰色GM(1,1)模型;粒子群算法;威布尔分布

截止2013年,我国电气化铁路总里程突破5.2万km,随着电气化铁路的大规模兴建,牵引供电系统的安全可靠运行问题日益突出,严重影响铁路的安全发展,因此对其可靠性问题进行深入研究,提高其可靠性显得尤为重要。

目前,牵引供电系统的可靠性研究已经取得了一定的成果。文献[1,2]采用故障树分析法分别对牵引供电系统接触网以及列车自动监控系统的可靠性进行分析,但对其相关组成部件的可靠性考虑不全面;文献[3]在原始数据缺乏的情况下,采用分段多项式法对设备的可靠性参数进行估计,并对其故障率特性进行了简单的分析,但由于原始数据偏少,导致建立模型失败的可能性较大;文献[4]运用Markov过程模型对接触网系统的可靠性进行了分析,但其分析的基础是设备的寿命服从指数分布;文献[5,6]采用威布尔分布作为牵引供电系统及其设备的可靠性分析模型,提出一种基于遗传算法的智能拟合方法,一定程度上提高了拟合的精度,但拟合优度检验结果不是十分理想;文献[7,8]将成功流法引入到牵引供电系统可靠性分析中,方法较为简便清晰。

本文针对牵引供电系统相关设备失效率数据相对较少的特点,在获得部分失效率样本的基础上采用灰色GM(1,1)模型对其进行中长期预测,在此基础上提出了一种以威布尔分布为可靠性模型,基于粒子群算法的智能拟合方法,并采用matlab编程实现了该过程,完成了牵引供电系统各主要设备的可靠性分析;采用故障树分析法对牵引变电所和接触网2个子系统进行可靠性分析并得到其可靠性模型,最后综合分析得到整个牵引供电系统的可靠性模型并计算得到其可靠度和平均使用寿命,为今后的维修计划提供了科学的依据。

1 基于灰色GM(1,1)模型的故障率预测

1.1 灰色GM(1,1)模型的特点

灰色理论以“部分信息已知,部分信息未知”的小样本、贫信息、不确定性系统为研究对象,通过对部分已知信息的生成和开发来提取有价值的信息,实现对系统行为、规律的正确认识和有效控制[9],GM(1,1)模型是作为一种最常用最有效的灰色预测模型,运用在时间序列上排列的数据建立模型,分析数据自身内在的规律性,进行预测,已被应用到工业、农业、能源等众多科学研究的大量实际问题中,取得了显著成果。本文中用来建模的故障率数据样本容量较小,导致建立威布尔分布模型失败的可能性极大,不利于牵引供电系统设备的可靠性分析,而采用灰色GM(1,1)模型对故障率数据进行预测,正好克服了这一缺点。

1.2 灰色GM(1,1)模型的建立

设原始数据序列为λ(0)=(λ(0)(1)、λ(0)(2)、…λ(0)(i)…、λ(0)(n)),对其进行累加生成新的数据序列,为λ(1)=(λ(1)(1)、λ(1)(2)、…λ(1)(j)…、λ(1)(n)),其中λ(1)(j)=∑ji=1λ(0)(i),j=(1,2,3,…,n)。

序列Z(1)=(z(1)(2)、z(1)(3)、…z(1)(k)…、z(1)(n))为λ(1)的紧邻均值生成序列,其中z(1)(k)=(λ(1)(k)+λ(1)(k-1)),k=2,3,…,n。

对累加后的数据序列λ(1)建立GM(1,1)模型的微分方程

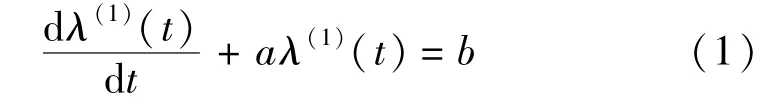
解上述微分方程得

其中,-a为发展系数;b为灰色作用量。

设参数向量^a=[a,b]T,且Y=[λ(0)(2)、λ(0)(3)、…λ(0)(n)]T,并且有

则可以用最小二乘法估计出^a的近似解为^a= (BTB)-1BTY。

将方程(2)还原得到预测函数为

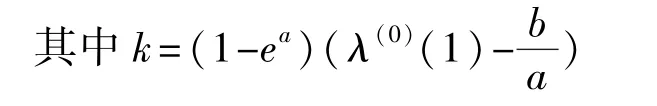
其预测流程如图1所示。

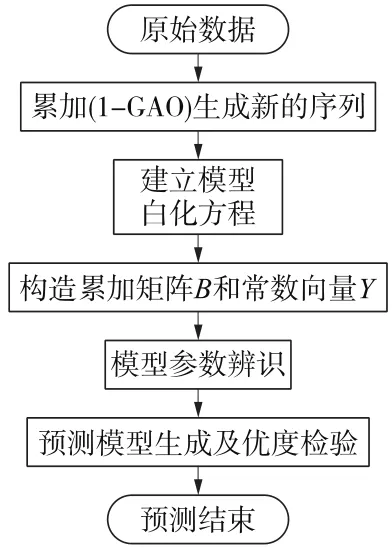
图1 预测流程

2 基于粒子群算法的智能拟合

由文献[10,11]可知威布尔分布是一种适用于描述牵引供电系统组成设备可靠性的概率分布模型之一,常用来进行设备的可靠性建模,本文采用双参数形式的威布尔分布进行牵引供电系统设备的可靠性建模,其可靠度函数和故障率函数分别为

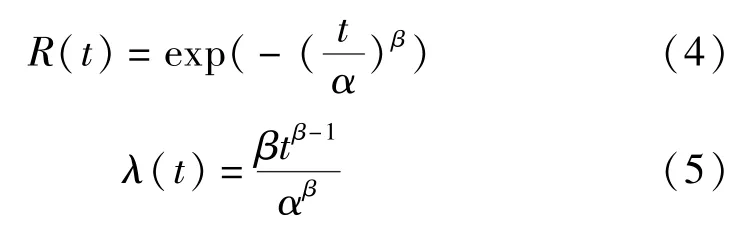
采用粒子群算法对故障率数据进行拟合,找到最优的威布尔分布的模型参数值。拟合的具体过程如下,拟合流程见图2。

(1)建立优化模型,确定目标函数的类型。取目标函数为

式中,λi与^λi分别为故障率的原始值和拟合值。

(2)设置算法的参数。速度更新参数c1=c2= 1.414 5,迭代次数=1 000,种群规模N=200。

(3)随机初始化粒子位置和粒子速度,并计算其粒子适应度值。

(4)根据初始粒子适应度值寻找个体极值和群体极值。

(5)更新粒子自身的速度和位置,迭代寻优。

(6)结果分析,找出最优的个体适应度值。

图2 拟合流程

3 模型应用实例

3.1 牵引供电系统主要设备可靠性分析

文献[3]收集了京广线郑州南段牵引供电系统(该系统共负责11个车站,约127 km线路的牵引电力供给,包括2个牵引变电所、2个AT所、1个开闭所和2个分区亭)主要设备168个月(12个月为一个统计单位)的故障率原始数据,如表1所示。

灰色GM(1,1)模型的特点是应用较少的数据建模,更重要的是不需要原始数据服从某个确定的概率分布,本文采用灰色GM(1,1)模型对108～168月的牵引供电系统相关设备的故障率数据进行模拟,得到各个设备的模型参数及模拟误差如表2所示。

由文献[12]可知,当发展系数-a≤0.3时,灰色GM(1,1)模型可用于中长期预测,因此利用已建立的灰色GM(1,1)模型对牵引供电系统各相关设备故障率进行预测,预测结果如表3所示。

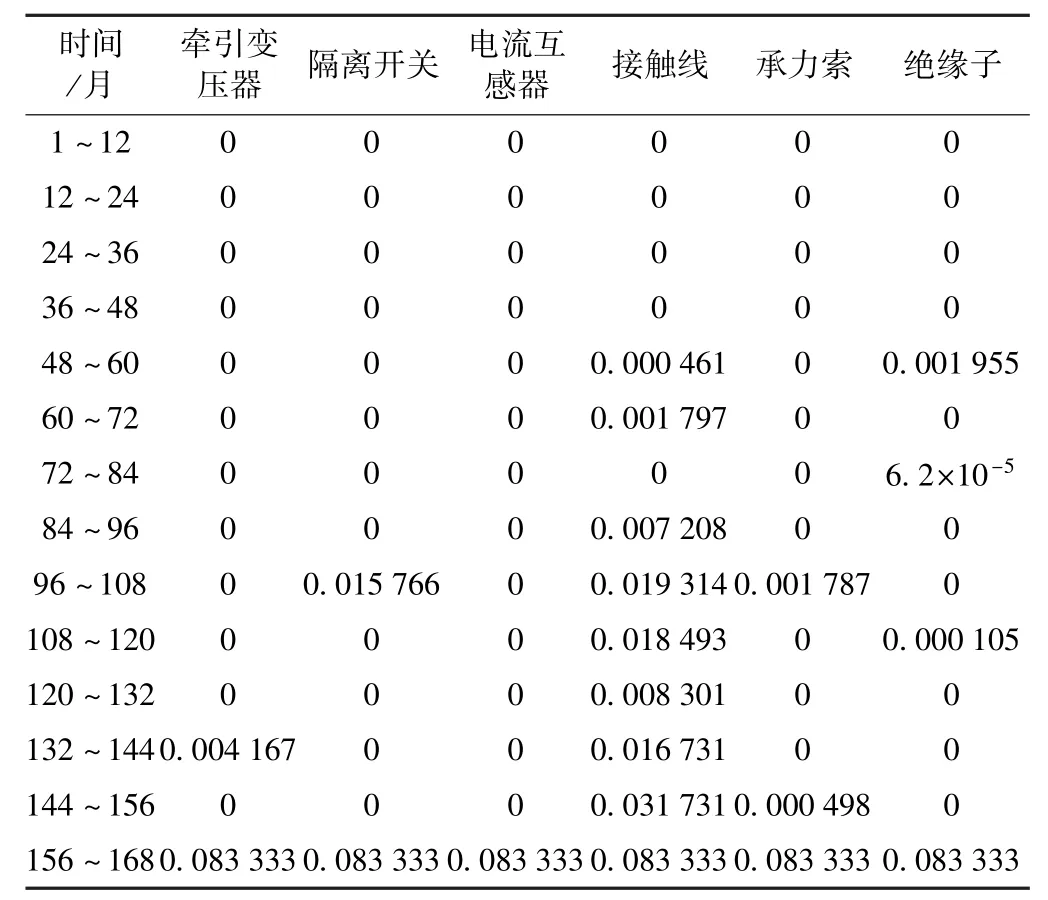
表1 原始故障率数据

表2 GM(1,1)模型参数及模拟误差

表3 故障率预测值

各设备的故障率预测值增大了建立其可靠性模型所需的样本数据,采用粒子群算法对各设备的故障数据进行拟合,可得到各设备可靠性模型的参数,同时对拟合结果采用K-S检验进行拟合优度检验,拟合优度检验结果、模型参数以及粒子群算法寻优过程的适应度值如表4所示。

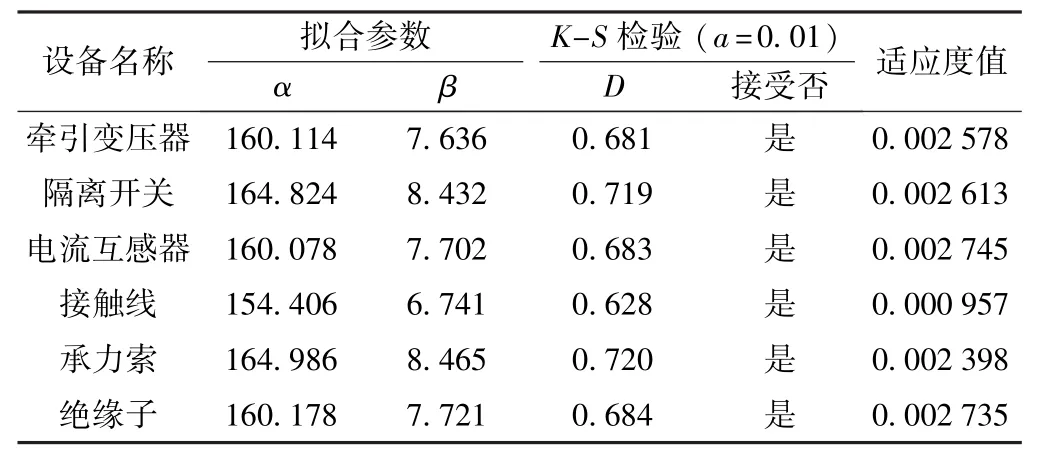
表4 可靠性模型参数及适应度值

通过所得到的可靠性模型,可以计算出168个月间每个设备故障率拟合的平均相对误差,与文献[4, 5]进行对比,其结果如表5所示。

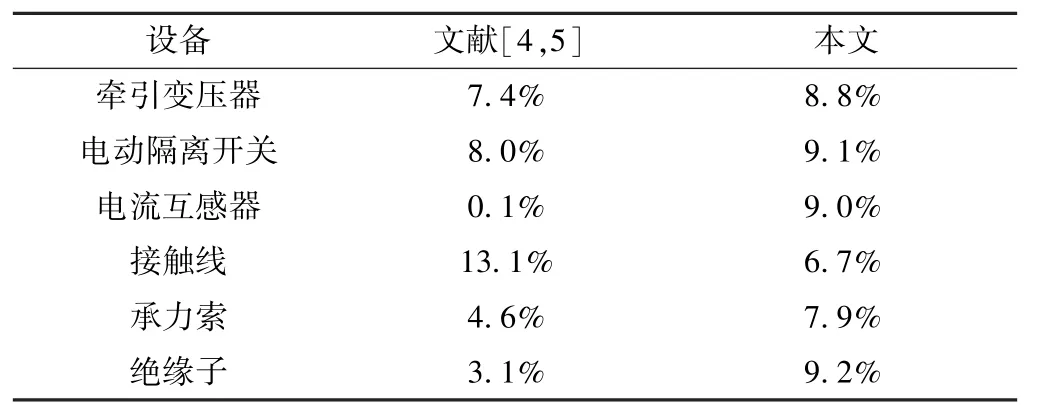
表5 拟合误差对比

由表4可知,本文所有设备的可靠性拟合结果均通过了K-S检验,而文献[4,5]中电流互感器和接触导线的拟合结果未能通过K-S检验,由表5可知文献[4,5]与本文所有设备的拟合精度都较高。这就有力地证明了本文所采用的在使用GM(1,1)模型预测相关设备故障率的基础上,基于粒子群算法的智能拟合方法是一种更加适合于牵引供电系统可靠性分析的方法。同时分析可知,拟合精度并不能直接说明所建模型的正确性,如文献[4]中的电流互感器,拟合精度极高,但未能通过可靠性检验,建模是失败的。究其原因为用来建模的数据属于截尾数据,没有完全显示出设备的寿命特征,这就从另一方面显示了灰色预测的必要性。

3.2 牵引供电系统整体可靠性模型的构建

本文以AT供电方式的交流牵引供电系统为研究对象,将其看作是一个不可修复的系统,并且认为其内部的单个设备的失效对其他设备无显著的影响。

牵引供电系统的结构复杂,对其整体进行可靠性分析十分困难,为避免建模过程过于繁琐复杂,因此将其从功能和结构上划分为牵引变电所和接触网两大子系统。利用故障树分析法,在牵引供电系统设备可靠性研究的基础上对这两个子系统分别进行可靠性建模,然后综合建立整个牵引供电系统的可靠性模型,并进行可靠性分析得到其平均使用寿命和可靠度。

3.2.1 牵引变电所的可靠性分析

由于电气化铁路牵引供电系统的上下行供电设备相同,其牵引变电所的主接线图可化简为如图3所示,其主要设备如表6所示。

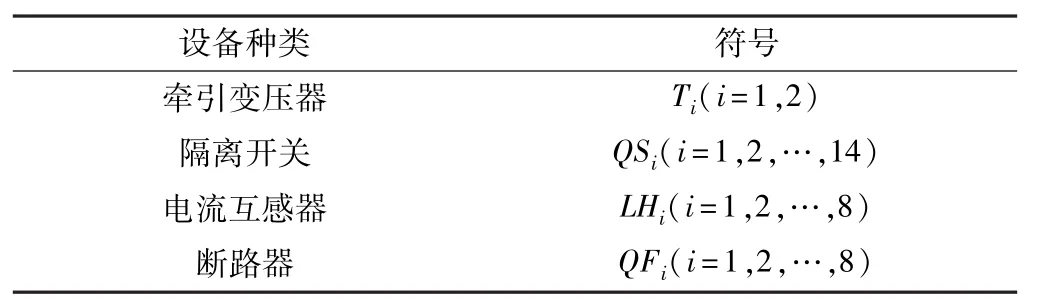
表6 牵引变电所主要设备

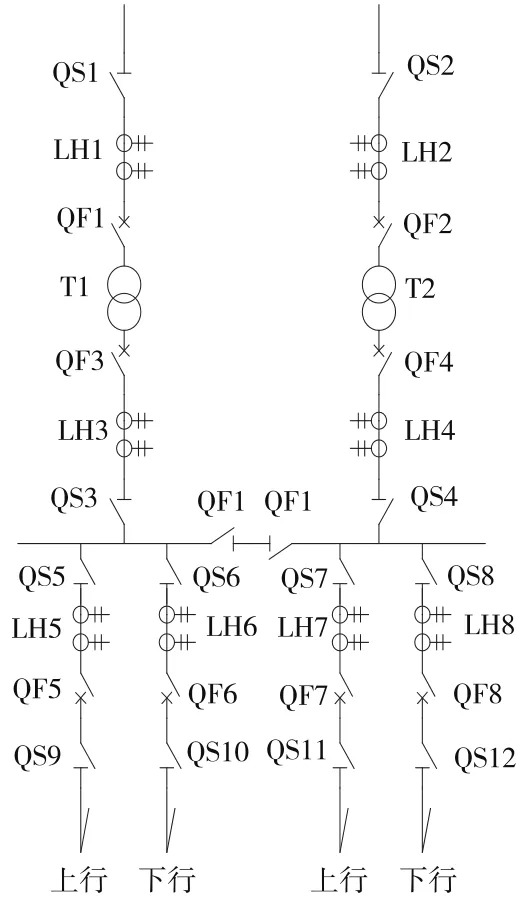
图3 牵引变电所主接线简化图

为使分析过程简洁明了,可将图3看成是元件的串联组合,组合后的故障率为组合前各元件的故障率之和,可表示为

由于BBD算法具有更高效率的结构以及基于这种结构的运算,BDD算法成为了解决故障树问题的一种有效工具[13],采用BBD算法可得到系统故障树的最小割集,进一步简化故障树模型,得到用最小割集表示的等效故障树,如图4所示。

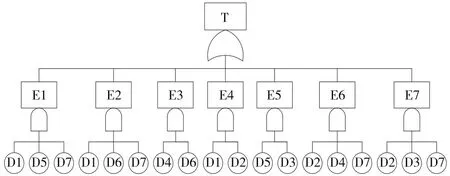
图4 牵引变电所最简故障树模型

由图4可得,牵引变电所故障树顶事件T发生的概率即其发生故障,不能向接触网区间正常供电的概率为

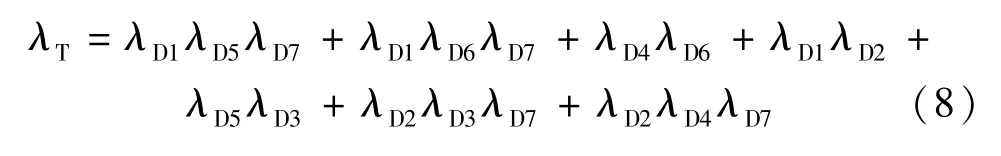
由式(8)可以计算出牵引变电所的故障率函数为

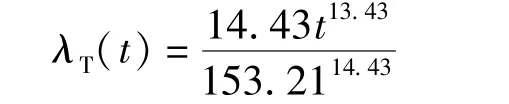
从而,其可靠度函数为

3.2.2 接触网的可靠性分析

接触网是牵引供电系统中一个重要的子系统,主要负责向电力机车受流,其主要设备包括接触导线、承力索、绝缘子、补偿器、中心锚段关节,在其组成结构上,可以认为它们是串行方式连接的,由于没有冗余配置,某一设备发生故障时,整个接触网系统将面临较大的失效风险。本文所研究的供电分区共有338组结构相似的区段,因此接触网的可靠度为

式中,Ri(i=1,2,3,4,5)分别为接触网各种设备的可靠度。

由式(9)可以算出接触网的可靠度函数为

3.2.3 牵引供电系统的可靠性分析

在牵引变电所和接触网可靠性分析的基础上,完成整个牵引供电系统的可靠性分析,其可靠度可表示为

最后计算出牵引供电系统的可靠度函数为

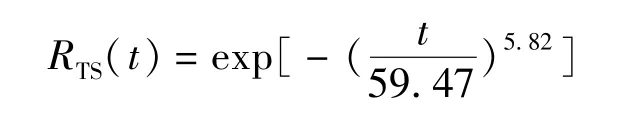
3.3 结果分析

通过拟合可以得到系统的可靠性模型,并计算得到评估年限中系统每年的故障率以及可靠度,继而计算出系统的平均使用寿命。平均使用寿命可以通过下式计算得到

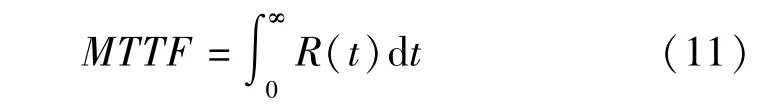
分别计算得到牵引变电所、接触网以及牵引供电系统整体的平均使用寿命分别为147.77、56.11、55.08个月。

图5为牵引变电所、接触网以及牵引供电系统整体的可靠度曲线图,由图5可知整个牵引供电系统的可靠度主要取决于接触网的可靠度,牵引变电所和接触网的可靠度随着使用时间的增长而下降,当分别运行了135、43个月之后,其可靠度明显下降,将严重威胁电气化铁路的安全运营。

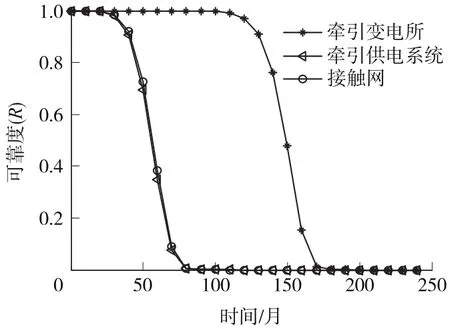
图5 系统可靠度曲线

4 结语

牵引供电系统各组成部分在运行过程中协调关系的不确定性以及相关零件材料性质在运动过程中随时间和荷载的变化而变化的特点,可以将它看成一个复杂的灰色系统,因此灰色GM(1,1)模型可以良好地对牵引供电系统各设备的故障率进行中长期预测,增大建立其可靠性模型所需的原始数据样本;基于粒子群算法的智能拟合,很大程度上提高了建模精度,对各设备可靠性模型进行的拟合优度检验结果十分理想,表明本文提出的方法是一种更加适合于牵引供电系统可靠性建模的方法。

[1] 赵琼,王思华,尚方宁.基于故障树分析法的接触网可靠性分析[J].铁道标准设计,2014(1):105-108.

[2] 朱爱红,杨亮,李博.基于故障树分析法的ATS可靠性仿真及应用[J].铁道标准设计,2013(11):105-109.

[3] 陈绍宽.铁道牵引供电系统维修计划优化模型与算法[D].北京:北京交通大学,2006.

[4] 万毅,邓斌,李会杰,等.铁路接触网系统的Markov分析[J].应用科学学报,2006,24(6):633-636.

[5] 谢将剑,吴俊勇,吴燕.基于遗传算法的牵引供电系统可靠性建模[J].铁道学报,2009,31(4):47-51.

[6] 谢将剑,吴俊勇,吴燕.牵引供电系统可靠性建模方法[J].交通运输学报,2008,8(5):23-26.

[7] 赵健.基于GO法的交流牵引供电系统可靠性研究[D].西安:西安理工大学,2010.

[8] 李军智.基于GO法的牵引变电所可靠性研究[D].成都:西南交通大学,2012.

[9] 于文东,赵进.基于灰色理论的加工中心可靠性分析[J].机床与液压,2012,40(13):193-195.

[10]杨媛.高速铁路供电系统RAMS评估的研究[D].北京:北京交通大学,2011.

[11]王灵芝.以可靠性为中心的高速列车设备维修决策支持系统研究[D].北京:北京交通大学,2011.

[12]刘思峰,党耀国,等.灰色系统理论及其应用[M].北京:科学出版社,2010.

[13]袁静,胡昌华,等.基于改进BDD算法的导弹安控系统故障树仿真分析[J].系统仿真学报,2007,19(1):9-12.

Research on the Reliability of Traction Power Supply System Based on Gray Theory and PSO

ZHANG Qing-ping,ZHAO Feng,WANG Si-hua
(School of Automation and Electrical Engineering,Lanzhou Jiao Tong University,Lanzhou 730070,China)

In order to increase the amount of sample data required to establish models and predict the failure-rate data of the relevant equipment in medium and long terms,gray GM(1,1)model is used based on particle swarm optimization(PSO)and a reliability modeling method of traction power supply system based on Weibull distribution model is proposed.Such models so established satisfy K-S goodness of fit test,and justify the feasibility of the method.The fault tree analysis(FTA)model of traction substation and catenary system in terms of minimum cut set is established by using binary decision diagram(BBD)algorithm,the reliability model of TPSS is obtained,and the reliability and the average useful time of system are calculated.The results of analysis demonstrate that the reliability of the traction power supply system as a whole depends largely on the reliability of catenary system,and provides a theoretical basis for future maintenance for traction power supply system.

Traction power supply system;Reliability;Gray GM(1,1)model;PSO;Weibull distribution

U223.6

A

10.13238/j.issn.1004-2954.2014.12.029

1004-2954(2014)12-0120-05

2014-04-17;

2014-04-28

中国铁路总公司科技研究开发计划课题(2013j010-E)

张庆平(1989—),男,硕士研究生,E-mail:13919078695@ 139.com。