基于随机解调器压缩采样的宽带频谱检测方法
罗昌林,许 翔
(嘉兴学院南湖学院,浙江嘉兴 314001)
基于随机解调器压缩采样的宽带频谱检测方法
罗昌林,许 翔
(嘉兴学院南湖学院,浙江嘉兴 314001)
宽带频谱检测的目的是完成对宽频段内信号的检测。在Nyquist采样理论下,为瞬时覆盖这么宽的带宽会对模数转换器(ADC,analog-to-digital)的采样率提出过高要求。研究了基于随机解调器压缩采样的宽带频谱检测方法。该方法能够以低于Nyquist采样率的速率完成对宽频段的采样,降低了ADC的负担。仿真结果表明,在频谱满足稀疏性的条件下,所研究的方法能够较准确检测宽频段内的各个信号。
频谱检测;随机解调器;压缩采样
0 引 言
宽带频谱检测是认知无线电的一大关键技术,也是通信侦察等军事应用的重要能力支撑。认知无线电中,由于次用户对频谱使用的优先级低于主用户,因此次用户需要利用宽带频谱检测(也称频谱感知)来找到当前频谱中未被主用户使用的频谱空穴[1,2]。而在通信侦察应用中,往往需要对宽频段内的各个信号进行快速搜索,以找到目标信号。
目前常用的宽带频谱检测方法有频域能量检测法、滤波器组法[3]、小波变换法[4]、多子带联合检测法[5]等。频域能量检测法先估计信号功率谱,再计算特定频率上的能量,进行判决。滤波器组法则采用多相滤波技术估计各个窄带信号的能量,相比于频域能量检测其复杂度要低。小波变换法对功率谱密度进行小波变换,找到功率谱密度的突变点,从而找到各个窄带信号的频率位置。多子带联合检测则对多个主用户信号进行联合检测,在实际条件下表现良好。这些方法所要求的采样系统均为传统的Nyquist采样。但是,宽带频谱检测要检测的频段通常很宽,要瞬时覆盖这么宽的带宽对模数转换器的采样率提出了过高的要求,当前商用ADC通常无法满足性能。为了降低对采样率的要求,人们提出利用压缩采样技术[6]来实现宽带频谱检测[7,8]。
随机解调器(RD,random demodulator)[9]是一种能够以低于Nyquist采样率实现对模拟信号采样的压缩采样技术。将随机解调器应用于宽带频谱检测需要满足频谱稀疏的条件。基于当前频谱利用率低下的局面,该条件往往能够得到满足。在讨论RD采样的基础上,研究了基于RD的宽带频谱检测方法,最后通过仿真分析该方法的性能。
1 随机解调器压缩采样
RD执行三个功能:解调、低通滤波及低速采样,其采样框图如图1所示[9]。
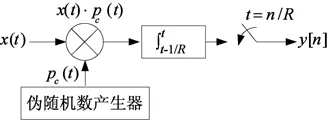
图1 RD采样框图
伪随机发生器产生离散时间序列ε0,ε1,…,其值以等概率取自±1,用来产生信号pc(t)

因此,pc(t)以Nyquist速率(即W)在±1间随机切换。然后,混频器将连续时间输入信号x(t)与pc(t)相乘得到

RD后面两个组件执行标准ADC的功能:低通滤波及采样。这里,低通滤波由累加器(积分器)实现。经过滤波的信号每隔1/R秒采一个点,得到采样序列{ym},ym为

RD最为关键的一点在于R要远远小于Nyquist速率W(即其为压缩采样),这样有利于采用低速ADC实现宽频带采样功能。
RD针对的信号模型为多音模型。令W/2为正整数,其值大于或等于待分析的连续信号x的最高频率,Nyquist频率fNYQ=W。假设K为单音数目。则包含各个单音信号的信号模型为

式中,F表示K个频率(值为整数)集合,其满足

{af:f∈F}为复值幅度集合。
令xn表示信号x(t)在时间段[tn,tn+1/W)内的平均值,tn=n/W,则



对于RD,有重要式(9)成立[9]

其中Φ是R×W维的RD矩阵,Φ=HDE,H为R×W维矩阵,H的第r行元素从第rW/R+1列开始有W/R个连续的1,其余均为0,其中r=0,1,…,R-1;D为W×W对角矩阵

RD压缩采样的重构问题即为根据已知的采样序列y及RD矩阵Φ,求解未知向量s的问题。由于R≤W,该问题为欠定问题,但是当未知向量s满足稀疏性条件时,该问题可以得到唯一的最优解。该重构问题在数学上可以表示为

压缩感知领域中,已有大量的重构算法可以用来求解该问题。
2 基于RD的宽带频谱检测方法
宽带频谱检测的目的是判断原信号x(t)的哪些频率被信号占用,哪些频率为噪声(频谱空穴)。本文采用重构后频域能量检测法。首先通过正交匹配追踪法(OMP,orthogonalmatching pursuit)[10]重构得到未知向量s,然后采用能量检测判断信号是否存在,即如果¯sf>λ,认为频率f被信号占用,否则为频谱空穴,其中 λ为判决门限。OMP算法流程见表1。

表1 OMP算法流程
3 仿真分析
仿真中假设频谱被划分成100个信道,W/R= 3,即采样率为Nyquist采样率的1/3。仿真中,主用户信号为二进制FSK信号,码速率为100 ks/s。噪声幅度服从均值为0、方差为某些值的正态分布。af在[6,12]之间随机取值。不同的信道占用数目下的检测概率和虚警概率,如图2所示,同时给出OMP的重构概率作为参考。噪声方差为0.015。门限η取值为幅度向量s中元素的幅度最小可能值的1/2。

图2 本文方法检测概率和虚警概率
由图可知,在重构概率接近于1的区域(即频谱稀疏的区域,图2中对应于信道占用数目小于等于11的时候),本方法的检测概率接近于1,虚警概率接近于0,从而说明了所研究方法的有效性。需要注意的是,当频谱不稀疏时,OMP算法重构概率很低,由此,检测概率也较低、虚警概率较高,这也进一步验证了RD压缩采样重构依赖的频谱稀疏这一条件。因此,在频谱不稀疏的场合,不适合应用RD压缩采样技术来实现宽带频谱检测。
不同噪声方差下的算法性能如图3所示。由图3可知,随着噪声方差的增加,算法性能会受到影响,特别是当噪声功率大于1时,检测概率下降明显,虚警概率上升明显。但是在噪声方差小于0.1时,本文方法性能非常优越。由此可知,基于RD的宽带频谱检测方法适用于噪声功率不是太大的场合。

图3 不同噪声方差下的算法性能
该研究方法与Nyquist采样的频域能量检测法的性能比较,如图4所示。由图4可知,相对于传统的以Nyquist采样率对款频段进行采样继而频域能量检测的方法来说,此方法在信噪比(SNR,signalto-noise ratio)上有所损失,这也是压缩采样技术内在的噪声折叠问题导致的。但是,当SNR较高时,该方法仍然能够获得可靠的检测性能,从而也进一步说明了基于RD的宽带频谱检测方法适用于噪声功率不是太大的场合。

图4 性能对比
4 结 语
研究了一种基于随机解调器压缩采样的认知无线电宽带频谱检测方法,该方法能够在低于Nyquist采样率的情况下对款频段进行检测,降低了ADC的负担。仿真结果表明,在频谱满足稀疏的条件下,该方法能够较准确检测各个信道的信号,完成对款频段的电磁频谱普查。当噪声功率增加时,检测性能有所降低,因此,该方法比较适合于信噪比不是太低的情况。另外,与所有压缩采样方法一样,基于RD的宽带频谱检测方法也需要在频谱满足稀疏度要求的情况下才适用。后续研究可以考虑绕过重构环节的检测方法,进一步降低复杂度。
[1]SUNH,NALLANATHAN A,WANGCX,etal.Wideband Spectrum Sensing for Cognitive Radio Networks:a Survey[J].IEEEWireless Communications,2013,20(2):74-81.
[2]AXELL E,LEUSG,LARSSON EG,et al.Spectrum Sensing for Cognitive Radio:State-of-the-art And Recent Advances[J]. IEEE Signal Processing Magazine,2012,29(3):101-116.
[3]FARHANG-BOROUJENY B.Filter Bank Spectrum Sensing for Cognitive Radios[J].IEEE Transactions on Signal Processing,2008,56(5):1801-1811.
[4]TIAN Z,GIANNAKISG.A Wavelet Approach to Wideband Spectrum Sensing for Cognitive Radios[C]//Proc. IEEE Cognitive Radio Oriented Wireless Networks and Communications,Mykonos Island,Greece,2006:1-5.
[5]QUAN Z,CUI S,SAYED A H,et al.Optimal Multiband Joint Detection for Spectrum Sensing in Cognitive Radio Networks[J].IEEE Transactions on Signal Processing,2009,57(3):1128-1140.
[6]DONOHO D.Compressed Sensing[J].IEEE Transactions on Information Theory,2006,52(4):1289-1306.
[7]ZENG F,LI C,TIAN Z.Distributed Compressive Spectrum Sensing in Cooperative Multihop Cognitive Networks[J].IEEE Journal of Selected Topics in Signal Processing,2011,5(1):37-48.
[8]YEN C P,TSAIY,WANG X.Wideband Spectrum Sensing Based on Sub-Nyquist Sampling[J].IEEE Transactions on Signal Processing,2013,61(12):3028-3040.
[9]TROPPA,LASKA N,DUARTE F,etal.Beyond Nyquist:Efficient Sampling of Sparse Bandlimited Signals[J].IEEE Transactions on Information Theory,2010,56(1):520-544.
[10]TROPP J,GILBERT A.Signal Recovery from Random Measurements Via Orthogonal Matching Pursuit[J].IEEE Transactions on Information Theory,2007,53(12):4655-4666.

罗昌林(1981—),主要研究方向为认知无线电、信号检测;
E-mail:luochanglin@139.com
许 翔(1963—),浙江嘉兴人,副教授,主要研究方向为无线通信、数字信号处理。
W ideband Spectrum Sensing Based on Random Demodulator Compressed Sampling
LUO Chang-lin,XU Xiang
(Nanhu College,Jiaxing University,Zhejiang Jiaxing 314001,China)
Wideband spectrum sensing aims at detecting signals in a wide frequency range.Under Nyquist sampling framework,a very high sampling rate of analog-to-digital converter(ADC)is required in order to cover such awide frequency range.A spectrum sensingmethod based on random demodulator compressed sampling is studied,which is capable of sampling a wide frequency range at sub-Nyquist rate,and therefore reducing the burden of ACD.Simulation results show that themethod can detect signals in a wide frequency range when spectrum is sparse.
spectrum sensing;random demodulator;compressed sampling
TN92
A
1673-5692(2014)03-300-04
10.3969/j.issn.1673-5692.2014.03.015
2014-03-24
2014-05-15

