并网运行的储能逆变器小信号稳定性分析

周丹，赵波，张雪松，汪科

（国网浙江省电力公司电力科学研究院，杭州310014）

输配电技术

并网运行的储能逆变器小信号稳定性分析

周丹，赵波，张雪松，汪科

（国网浙江省电力公司电力科学研究院，杭州310014）

储能系统是目前平抑间歇式可再生能源功率波动的一种有效手段。推导了并网运行模式下储能逆变器的小信号数学模型，分析了主要控制参数对逆变器并联运行小信号稳定性的影响，并利用PSCAD搭建了并网运行的储能逆变器仿真模型，验证了逆变器控制参数对系统小信号稳定性的影响。

储能系统；并联运行；小信号稳定性；控制参数

目前，多数可再生能源诸如太阳能、风能等，具有不均匀性和不可控性等特点，转换输出的电能随时可能发生变化，由此造成发电的间歇性和波动性给电力系统的运行带来了不利的影响[1]。采用一定容量的储能装置与可再生能源发电装置联合运行，集成并网，通过实时调整储能系统的充/放电功率以及充/放电状态的迅速切换，使可再生能源随机变化的输出功率转换为相对稳定的平滑输出，从而保证电网的安全稳定运行。这种方式实质上是通过储能系统发出与可再生能源波动分量反向的输出功率来平抑波动，这对储能系统在小扰动下的稳定性提出了较高的要求，所以储能系统的小信号稳定性就成为一个重要的研究内容[2-4]。

由此建立了并网运行模式下的储能逆变器小信号模型，利用特征值法分析了并网运行的储能逆变器直接无穷大电源时的小信号稳定性，研究了相关控制参数、滤波器参数对系统小信号稳定性的影响。利用PSCAD仿真软件搭建了仿真模型进行了时域仿真，仿真结果验证了理论分析的正确性。

1 并网运行模式的储能逆变器

并网运行的储能逆变器控制结构如图1所示，主要包括功率控制环、LCL滤波器、脉冲发生电路、开关桥电路及电压/电流反馈环、锁相环（PLL）、abc-dq0坐标变换（park变换）等部分。图中，vi为逆变器全桥电路的输出端电压；v0为LCL滤波器电容电压；vMG为母线电压；idref和iqref分别为储能逆变器有功电流和无功电流指令值；id和iq分别为有功电流和无功电流反馈值；rf，Lf，rc，Lc，Cf为LCL滤波器电感电容参数；il为流过电感Lf的电流；i0为流过电感Lc的电流；ω为电压电流角频率。

功率控制环的控制流程如图2所示，kqd3，kqp3为功率控制环比例系数；kid3，kiq3为功率控制环积分系数；vd_out，vq_out为功率控制环输出给脉冲发生电路的调制信号；L为LCL滤波器电感值。

图1 并网运行的储能逆变器结构

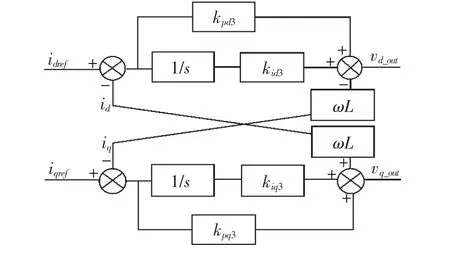
图2 功率控制环

将系统施加小扰动后，通过线性化处理建立功率控制环的小信号模型，如式（1）所示：

式中：状态变量xu=[ΦduΦqu]T，为输入变量；uu1= [idrfiqref]T，uu2=[idiq]T，为输出变量；yu=[vd_outvq_out]T，

储能逆变器滤波器环节的小信号模型见式（2）：

式中：xf=[ildilqvdvqidiq]T，为状态变量；Δωref为输入量；uf1=[vd_outvq_out]；uf2=[vMGdvMGq]T；输出量为ycon=[idiq]T；

储能逆变器完整的小信号数学模型输入量取自逆变器输入参考电流、母线电压及其角频率：

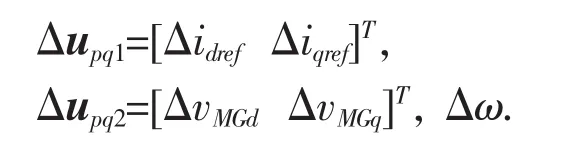
输出量为：

状态变量为：

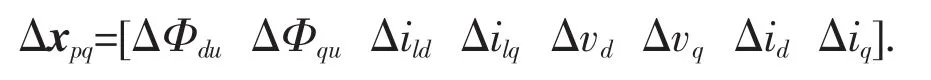
所以，其小信号模型可以写成式（3）：

式中：

Af1，Af2，Af3分别是Af的第12列、第34列、第56列；

当并网运行的储能逆变器与无穷大电源相连，如图3所示。

图3 储能逆变器连接无穷大电源

图3中无穷大电源的输出电压就是储能逆变器出口母线处的电压，即

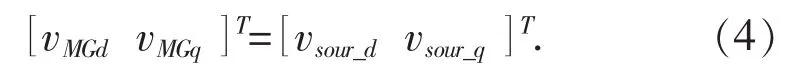
把式（4）代入式（3）表示的储能逆变器小信号模型后，可得图3中系统的小信号模型为：

2 并网运行储能逆变器的小信号分析

2.1 系统参数的设置及特征值

系统参数设置如表1所示。

根据以上参数设置可以求得式（5）的系统特征值，如表2所示。

表1 系统参数

表2 特征值

该系统的特征值共有4对复数根，其中第1与2对特征值靠近虚轴，虚部较大，振荡频率较高，第3与4对特征值离虚轴较远，阻尼相对较大，虚部小，振荡频率低。

2.2 控制参数对系统特征值影响分析

当其他控制参数固定，比例系数kpd3与kpq3从0.01～5变化时，系统的根轨迹如图4所示。第1与2对特征值的实部随比例系数kpd3与kpq3增大向远离虚轴方向运动，kpd3与kpq3较小时，这2对特征值会引起系统不稳定；第3与4对特征值的实部随kpd3与kpq3增大而增大，当kpd3与kpq3大于0.2时，特征值的实部开始大于0，系统开始不稳定。kpd3与kpq3取0.05～0.1比较合适。

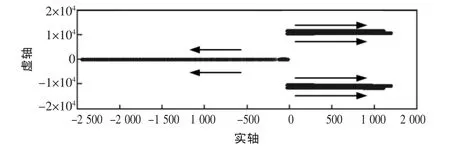
图4 kpd3，kpq3与系统根轨迹关系

当其他控制参数固定，积分系数kid3与kiq3变化时，系统的根轨迹如图5（a）所示。当从1～150变化时，有2对特征值变化比较明显，其根轨迹如图5（b）所示，kid3与kiq3从20开始，2对特征值的实部基本不再变化，所以kid3与kiq3取20～40比较合适。

图5 kid3，kiq3与系统根轨迹关系

3 时域仿真及结果分析

3.1 仿真模型及参数设置

为了验证小信号分析结果的正确性和有效性，在PSCAD中建立了仿真模型如图6所示，仿真参数设置与表1参数一致。

图6 系统仿真模型

3.2 控制参数对系统运行稳定性影响

其他参数按表1设置，比例系数kpd3与kpq3分别取0.01，0.1，1时，有功功率参考值在1 s时发生突变，系统输出三相电流波形及功率如图7所示。当kpd3与kpq3为0.01时，系统失稳，根据根轨迹分析结果可知，主要是由图4中的第1与2对特征根太靠近虚轴引起；当kpd3与kpq3为0.1，有功功率参考值发生波动时，系统仍能保持稳定；

图7 不同的kpd3与kpd3时PCS输出波形

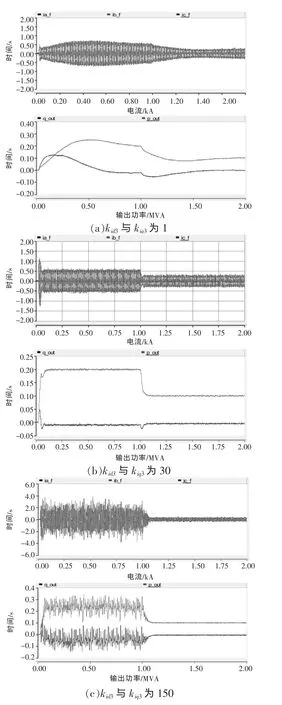
图8 不同的kid3与kiq3时PCS输出电压波形

当kpd3与kpq3为1时，系统失稳。根据根轨迹分析结果可知，主要是由图4中的第3与4对特征根实部已经大于0引起。

其他参数按表1设置，积分系数kid3与kiq3分别取1，30，150的时候，负载在1 s时发生突变，系统输出三相电流波形及功率输出如图8所示。当kid3与kiq3为1，负载发生波动时，系统输出电流波形没有失真，但输出功率到达稳态值的调整时间非常长；当kid3与kiq3为30，负载发生波动时，系统仍能保持稳定，此时输出电流经过0.05 s左右就已达到稳态值；当kid3与kiq3为150时，系统负载较大时出现了高频振荡分量，系统稳定性变差。

4 结论

主要研究了并网运行的储能逆变器小信号稳定性问题，通过特征值分析法，分析了采用PI控制时控制参数对逆变器并联运行小信号稳定性的影响，获得的主要结论有：

（1）比例系数对系统小信号稳定影响很大，过大或过小的参数设置都会使储能逆变器失稳；

（2）积分系数对系统达到稳态值的调整时间影响较大，积分系数过小会造成调整时间很长，储能逆变器对指令的响应速度过慢，另外，积分系数很大时也会造成系统不稳定。

[1]丁菲.含多种分布式电源和储能的低压微网系统的暂态建模与仿真[D].天津：天津大学，2010.

[2]肖朝霞，王成山，王守相.含多微型电源的微网小信号稳定性分析[J].电力系统自动化，2009，33（6）∶81-85.

[3]高范强，王平，李耀华，等.基于时变相量小信号模型的逆变器并联控制系统分析与设计[J].中国电机工程学报，2011，31（33）∶75-84.

[4]张明锐，黎娜，杜志超，等.基于小信号模型的微网控制参数选择与稳定性分析[J].中国电机工程学报，2012，32（25）∶9-19.

（本文编辑：陆莹）

Analysis on Stability of Small Signal for Grid-connected Energy Storage Inverter

ZHOU Dan，ZHAO Bo，ZHANG Xuesong，WANG Ke
（State Grid Zhejiang Electric Power Research Institute，Hangzhou 310014，China）

Energy storage system is an effective means for stabilizing power fluctuations of intermittent renewable energy.This article derives small signal mathematical model of energy storage inverter in grid-connected operation and analyzes the impact of main control parameters on small signal stability of inverter；furthermore, it uses PSCAD to build a simulation model of the operating grid-connected energy storage inverter，for the purposes of verifying the impact of inverter control parameter on small signal stability.

energy storage system；grid-connected operation；small signal stability；control parameter

TM133

：A

：1007-1881（2014）01-0001-04

2013-09-18

周丹（1983-），男，浙江桐庐人，博士，工程师，主要从事分布式电源和微电网相关技术的研究。