接入风电场的电力系统无功优化研究
彭涛,王斌,蔡昌春
(1.国家电网苏州供电公司,江苏苏州215011;2.河海大学,江苏常州213022)
接入风电场的电力系统无功优化研究
彭涛1,王斌1,蔡昌春2
(1.国家电网苏州供电公司,江苏苏州215011;2.河海大学,江苏常州213022)
研究了考虑大型风电场接入的电力系统无功优化问题。针对风电场接入时的无功优化模型,分析讨论了接入风电场的系统无功潮流计算,提出了一种改进遗传算法解决传统遗传算法在无功优化中面临的问题。采用混合编码方式处理连续变量和离散变量共存,利用自适应交叉和变异操作提高算法的搜索能力和跳出局部最优解的能力,利用精英代保持进化策略提高算法的可靠性和鲁棒性,在IEEE30标准系统引入风电场验证了该算法的适用性。
电力系统;无功优化;分布式发电;潮流计算;遗传算法
0 引言
电力系统无功功率平衡是保证电力系统电压质量的必要条件,可通过调节发电机端电压、投切电容器组或电抗器组和可调变压器分接头优化电网无功潮流,改善电压质量、减少网络损耗和提高电压稳定性[1]。基于可再生能源的分布式发电系统技术日益成熟,成为未来电力系统的有力补充,随着分布式能源的大量接入将影响传统电力系统的各个方面,无功电压控制将是其中一个重要的问题[2]。分布式发电的随机性必然对系统潮流大小和方向产生影响,并影响电压调节设备正常工作,使系统电压波动频繁,严重影响系统电能质量。
无功优化问题是一个高维、离散、有约束非线性组合优化问题,因此,无功优化问题的求解相对较困难。传统无功优化问题的求解方法主要有线性规划[3]和非线性规划[4]。线性规划在处理无功优化时需将目标函数和约束函数线性化,若迭代步长选取不合适,可能会引发振荡或收敛缓慢。非线性规划能直接处理非线性的目标函数约束函数,但非线性规划目前还没有一个非常成熟的算法。针对无功优化问题的非线性、多约束、控制变量的离散性和连续性并存等特点,智能算法如遗传算法、粒子群算法、蚁群算法在无功优化的求解过程中得到了广泛的应用[5-7]。
在传统无功优化模型的基础上,分析了大型风电场接入对电网无功电压控制的影响,提出了一种考虑风电场并网接入的无功优化模型。针对遗传算法在处理无功优化过程中的问题,通过混合编码、自适应交叉和变异率、倒位操作以及精英代保持进化策略等改进措施,提高遗传算法的收敛性。最后,在标准IEEE0节点系统中接入大型风电场,验证算法的合理性和适用性。
1 无功优化数学模型
1.1 无功优化模型
静态无功优化目标函数包括经济目标、电压水平目标及安全性目标等。以有功网损最小为目标函数建立无功优化模型:
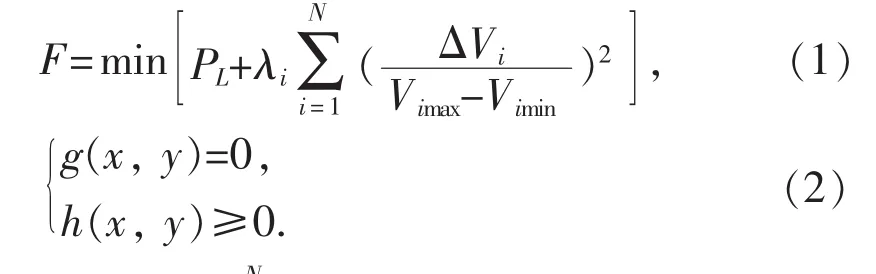
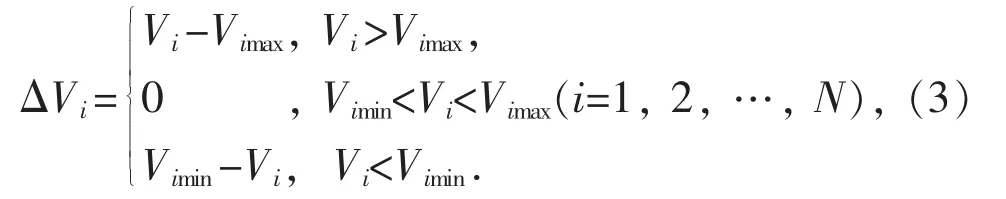
式(2)中等式约束条件g(x,y)为潮流平衡方程,即节点i注入的有功和无功功率应满足如式(4)约束:
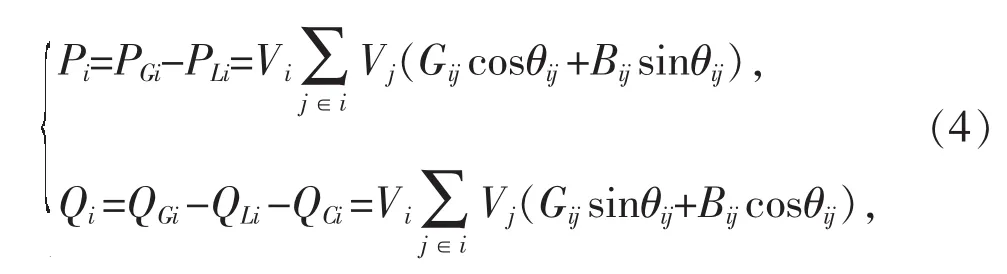
式中:Pi和Qi表示节点i注入的有功和无功功率;PGi和QGi分别为发电机节点i的有功和无功出力;PLi,QLi和PCi分别表示节点i的有功负荷、无功负荷和无功补偿容量。
式(2)中不等式约束h(x,y)≥0包含支路电流、发电机出力、节点电压、可调变压器分接头变化、电容器(电抗器)投切容量等限制。在无功优化问题中选取发电机机端电压VG、容性无功补偿容量QC以及可调变压器分接头Tl作为控制变量,选取发电机无功出力QG、节点电压幅值Vi和系统支路电流IL为状态变量。控制变量约束方程:
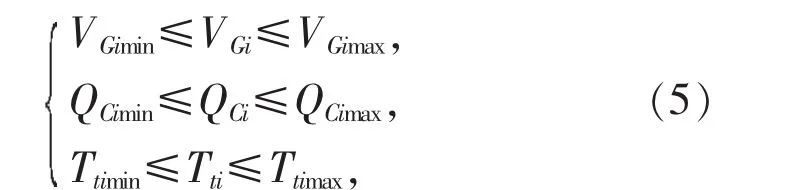
式中:VGimin和VGimax分别为发电机端电压上、下限;QCimin和QCimax分别为容性无功补偿容量的上、下限;Ttimin和Ttimax分别为可调变压器分接头位置的上、下限值。
状态变量约束方程:
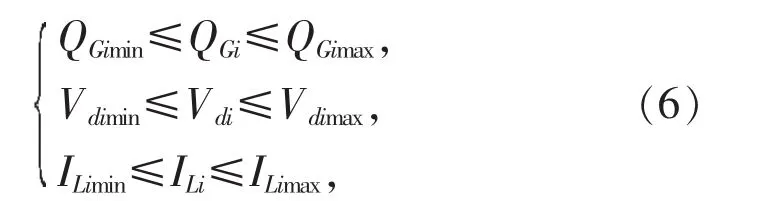
式中:QGimin和QGimax分别为发电机无功功率的上、下限;Vdimin和Vdimax分别为节点电压幅值的上、下限;ILimin和ILimax分别为支路电流的上、下限。
1.2 风电场并网潮流模型
风电机组多为异步发电机,其等值电路见图1,在进行潮流计算时常用PQ模型。PQ模型是根据风电场的有功功率和给定的功率因数来估算风电场吸收的无功功率,将其作为1个普通的负荷节点参与潮流计算。PQ模型的优点是潮流计算第1次迭代时有功功率是风速的函数,并被视之为常数,无功功率仅取决于功率因数,由于没有考虑风机内部参数,容易造成计算误差。由异步电机稳态功率方程可知,风力发电机的输出有功功率由风机决定,而风机吸收的无功功率和风电场输出有功功率以及风力发电机初始滑差、接入母线电压有关。因此,在潮流计算过程中必须综合考虑有功、无功之间的关系,而不能简单地将其定义为PQ节点模型。
风电场输出有功功率由风机功率决定,风力发电机输出的机械功率Pw可以表示为:

式中:S为风机叶片扫掠面积;ρ为空气密度;v为风速;Cp为风力机的风能利用系数。
风力发电机的输出功率与受风面积以及风速的3次方成正比,跟风机的电气参数无关,因此只要确定风速以及风机的物理参数就可得到风机的理论输出功率。
图1中V为异步发电机机端电压;R1为定子电阻;X1为定子电抗;Xm为励磁电抗;Rr/s为机械负载等效电阻;X2为转子电抗;s为转差率。
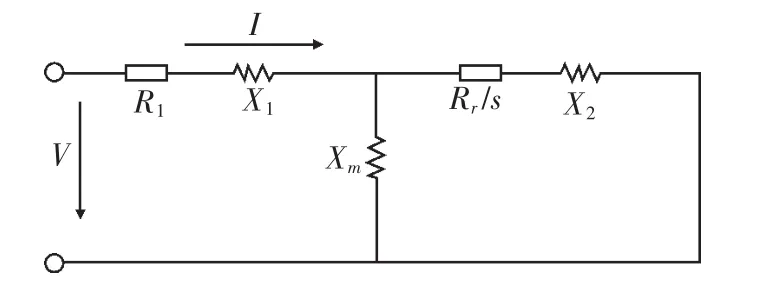
图1 异步发电机等值电路
忽略定子电阻,异步发电机输出的电磁功率Pw和tgφ分别为:
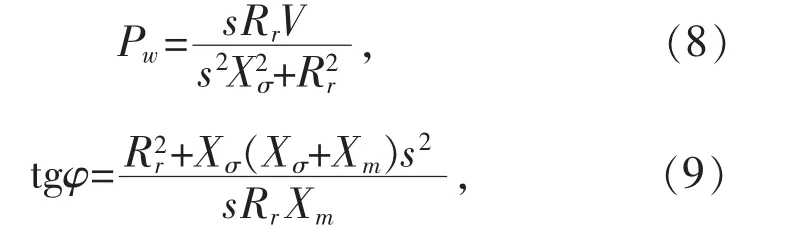
式中:φ为功率因数角;Xσ=X1+X2。
同时,异步发电机转差率s为:
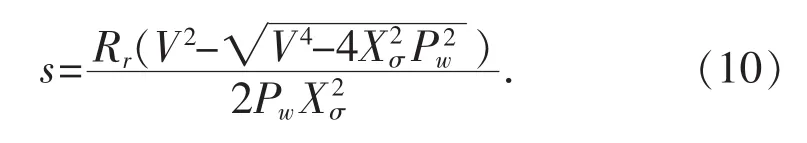
由此可得异步风力发电机吸收的输出功率Q为:
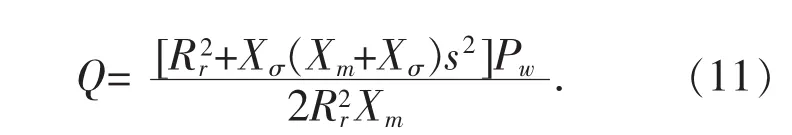
由式(11)可知,异步发电机吸收的无功功率为有功功率和母线电压幅值的函数,其中有功功率可以由风速确定。因此在潮流计算时,只需将风电场节点视为特殊的PQ节点,其注入的无功功率为节点电压的函数,在形成雅克比矩阵时补充风电场注入节点无功对电压的导数,以修正雅克比矩阵J=∂θ/∂V。
由无功功率的计算公式可得无功对电压的偏导:
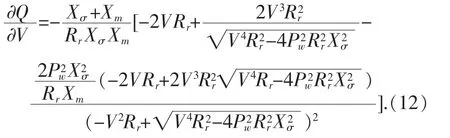
2 基于改进遗传算法的无功优化
2.1 混合编码
由于无功优化问题中既包含离散变量也包含连续变量,因此,利用浮点数编码和二进制编码相结合的编码方式分别处理连续变量和离散变量。其中发电机机端电压为连续变量,电容器投切和变压器分接头档位为离散变量。在离散变量编码时,根据电容器投切组数以及变压器分接头档位数进行二进制编码。比如,共有7组电容器投切,变压器的可调分接头有15档,可以用3位二进制数表示电容器投切组数,4位二进制数表示变压器档位。
2.2 自适应的交叉率和变异率
交叉和变异是维持个体多样性的重要保证,较大的交叉可以提高算法的搜索能力,但是会增加算法的随机性;变异能够使算法跳出局部最优解,较小的变异率会导致群体多样性的降低。因此,采用自适应的交叉和变异,在算法的初期尽量扩大搜索范围,增加搜索空间,降低早熟;在算法后期能够有效地跳出局部最优解,使算法更具有鲁棒性和全局最优性。自适应变异率Pc如式(13)所示:
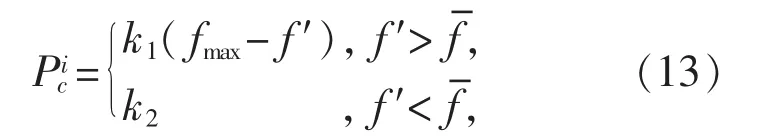
变异率采用渐变的Signoid函数,如式(14)所示:
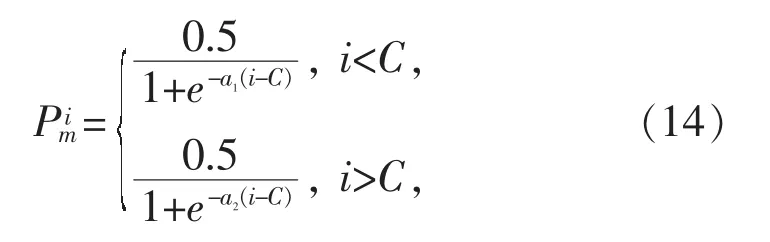
为了保证种群的多样性防止提前收敛,通过动态调整C来达到目的,即算法初期时,C较大,使种群个体能够通过交叉充分混合,算法进入后期,减少C使种群中较多个体具有较大变异率,增强种群探索能力。
2.3 倒位算子
倒位操作是指颠倒个体编码随机指定的2个基因座之间的基因排序,从而形成新的染色体。倒位操作改变了个体编码串中的部分基因排序,使遗传算法更有利于生成较好的模式。
2.4 精英代保留策略
在遗传算法中通过个体的交叉、变异不断产生新的个体,同时也会产生越来越多的优良个体。但是由于选择、交叉、变异的随机性,也可能破坏种群中适应度较好的个体,采用最优个体保存策略进化,将优良基因得以保存并进行遗传操作,使得最优个体的优良基因能够在进化中不被淘汰。
3 仿真分析
为了验证算法的合理性和适用性,采用IEEE-30节点标准系统作为算例系统(见图2),其中风电场通过110 kV线路接入系统的17节点母线,风电场中包含100台额定容量为600 kW的异步风力发电机,风力发电机参数如下:定子电抗X1=0.099 85 p.u(p.u为标幺值),定子电阻r1= 0.008 33 p.u,转子电抗X2=0.109 06 p.u,转子电阻r2=0.003 73 p.u,励磁电抗Xm=4.547 08 p.u,额定转差s=-0.004,额定功率因数=0.89。风力发电机参数的基准值为其自身额定容量,系统功率的基准值为100 MVA。
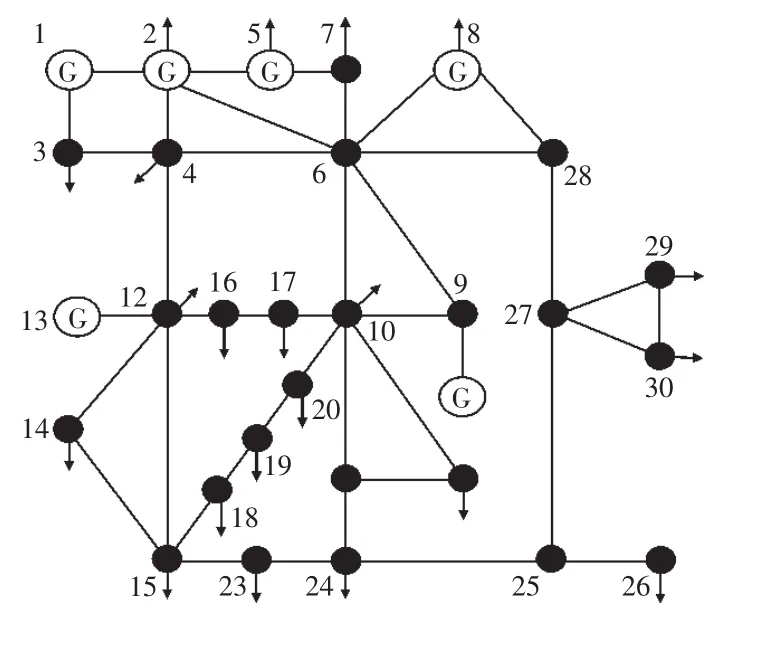
图2 IEEE 30节点电力网络系统
由图2可知,IEEE-30系统中有41条支路、6个发电机节点和22个负荷节点。发电机节点号为1,2,5,8,11,13,节点1为平衡节点,其余为PV节点。可调变压器支路为L6-9,L6-10,L4-12,L27-28,电容器补偿点有9个,分别连接在10,12,15,19,21,24,26,27,30。
为了验证算法的可靠性,通过对比风电场接入前后系统有功损耗来验证。当风电场接入系统运行后,风电场在输出有功功率同时吸收大量的无功功率,风电场功率的输出改变了整个系统潮流,从而影响无功电压控制策略和方式。随着风电场输出功率的不同,其吸收无功功率的量也不同。在风电场不同输出功率条件下,对风电场接入系统后进行无功优化计算,得出不同风电场输出功率下的无功优化结果。表1给出了不同风电场输出功率时对系统有功损耗的影响。

表1 不同风电场输出功率下的系统有功损耗p.u
由表1可知,随着风电场输出功率的增加,风电场吸收的无功功率也随之增加。当风电场输出功率从0.3 p.u增加至0.6 p.u时,风电场吸收的无功功率从0.132 p.u增加至0.264 p.u。当风电场接入后,系统运行状态将改变,通过无功优化将有效降低系统有功损耗。
表2,表3给出了当风电场输出功率为0.3 p.u时,系统发电机端电压和变压器档位优化前后的对比,优化后系统电压都在合理范围内,没有越限。
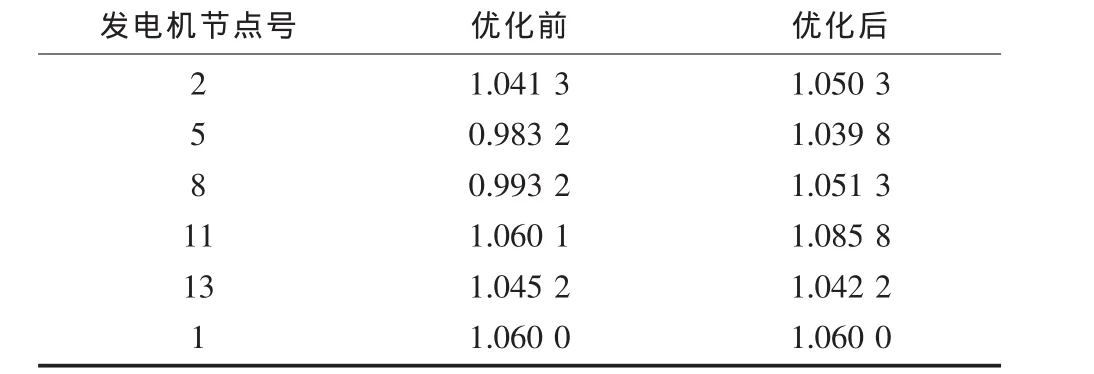
表2 发电机端电压优化前后对比p.u
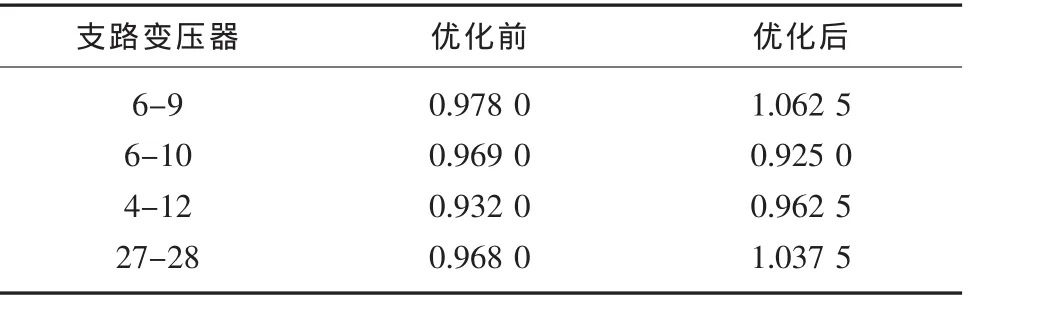
表3 变压器档位优化前后对比p.u
4 结语
随着分布式能源技术的不断提高,越来越多的分布式发电机组并入电网,由此对电网的安全稳定必然带来影响。着重研究了大型风电场接入对于电力系统无功电压控制的影响,分析了风电场接入的潮流计算模型、无功优化模型,应用改进遗传算法进行求解。通过仿真系统的算例验证了提出算法的合理性和有效性,能够在保证系统安全的情况下最大限度的降低系统损耗,提高系统运行的安全性和经济性。
[1]张鹏,刘玉田.配电系统电压控制和无功优化的简化动态规划法[J].电力系统及其自动化学报,1999,11(4)∶49-53.
[2]韦钢,吴伟力,胡丹云,等.分布式电源及其并网时对电网的影响[J].高电压技术,2007,33(1)∶36-40.
[3]E HOBSON.Active and reactive power security control us ing successive linear programming[J].IEEE Trans On Power Apparatus and System,1982,101(1)∶644-654.
[4]张文,刘玉田.自适应粒子群优化算法及其在无功优化中的应用[J].电网技术,2006,30(8)∶19-24.
[5]娄素华,熊信银,吴耀武.电力系统无功优化的变尺度混沌优化算法[J].电网技术,2005,29(11)∶20-25.
[6]HIROTAKA YOSHIDA,KENICHI KAWATA.A particle swarm optimization for reactive power and voltage control considering voltage security assessment[J].IEEE Trans on Power Systems,2000,15(4)∶1232-1239.
[7]张勇军,任震,钟红梅,等.实时无功优化调度中的邻域搜索改进遗传算法[J].电网技术,2003,27(1)∶22-25.
(本文编辑:陆莹)
Research on Reactive Optimization of Power System Connected to Wind Farm
PENG Tao1,WANG Bin1,CAI Changchun2
(1.State Grid Suzhou Power Supply Company,Suzhou Jiangsu 215011,China;2.Hohai University,Changzhou Jiangsu 213022,China)
Reactive optimization of power system connected to large wind farm is investigated in this paper. Calculation on reactive power flow of the system connected to wind farm is analyzed and discussed.The paper proposes an improved genetic algorithm to solve problems in conventional reactive power.The mixed code approach is employed to coordinate the coexistence of continuous variables and discrete variables.By using selfadaptive crossing and mutation,the abilities of searching and skipping from local optimal solution;by using elite generation,the revolution strategy is maintained to improve the reliability and robustness of the algorithm. In the final,the wind farm is introduced to IEEE30 to verify the effectiveness and adaptability of the method.
power system;reactive power optimization;distributed generation;power flow calculation;genetic algorithm
TM732
:A
:1007-1881(2014)01-0009-04
江苏省输配电装备技术重点实验室开放基金资助(2011JSSPD11)
2013-09-09
彭涛(1980-),男,江西泰和人,助理工程师,主要研究方向为电力系统运行与控制。

