提升机故障诊断不确定性推理方法

李娟莉,杨兆建

(太原理工大学机械工程学院,山西太原 030024)

提升机故障诊断不确定性推理方法

李娟莉,杨兆建

(太原理工大学机械工程学院,山西太原 030024)

针对提升机故障诊断过程中的若干不确定性问题,提出一种新的基于本体和贝叶斯网络的故障诊断不确定性知识融合推理方法。该方法对本体贝叶斯网络进行了形式化的定义,运用OWL本体语言扩展了本体对领域知识的不确定性表示,通过一系列的翻译规则和程序,实现了本体结构到贝叶斯网络结构的转换;然后建立了基于本体和贝叶斯网络的融合推理模型,利用本体推理完成对故障诊断本体知识的语法检查、语义一致性的验证以及本体的解析,采用基于启发式搜索树的贝叶斯网络进行不确定性推理,并在贝叶斯网络可视化推理平台Netica上进行了验证。矿井提升机制动系统故障诊断实例表明,该融合推理模型具有较好的故障识别效果,处理所得的诊断结果具有较高的可信度。

贝叶斯网络;本体;提升机;故障诊断;不确定性推理

提升机在运行过程中,由于其自身结构的复杂性、运行条件的特殊性和其它各种因素的影响,不可避免地发生各类故障,甚至是多发关联故障。目前很多提升机故障诊断系统在实际中得到了应用,并在设备技术维护中发挥了重要的作用,但现有的很多系统仍然面临着一些问题,如对提升机故障诊断概念、诊断问题描述、诊断知识的处理等方面没有统一的描述,在知识的表示、获取和更新方面没有形成统一的认识和规范,不能完全适应系统诊断推理的需求,且系统的异构性使相互之间缺乏共同的理解。因此,提升机故障知识库的构建和故障知识的描述问题有待进一步的研究。在人工智能研究领域,本体能够以一种明确的、形式化的方式来表示领域知识,提高异构系统间相互交流学习的能力,已经成为知识工程领域中一种有效的理论指导和实践工具。鉴于此,国内外不少学者开始将本体理论应用于故障诊断,并进行了进一步的探索[1－3]。

虽然本体作为一种能在语义和知识层次上描述知识的建模工具,提供了共享概念模型形式化的规范说明,为知识的共享和使用奠定了基础,但本体不能表示实际应用中存在的不确定信息,也不能支持模糊信息的推理。为了解决这一问题,国内外众多学者在本体语言OWL的概率扩展和模糊扩展方面进行了诸多研究,从而使本体能表示不确定知识,并进行有效推理。在不确定性推理方面,贝叶斯网络推理是目前最有效的方法之一,它是一种概率推理方法,能解决数据间不一致甚至相互独立的问题,使推理结果更为准确可信[4]。因此近年来,对Web本体语言的概率扩展研究,主要集中在把Web本体语言和贝叶斯网络相结合的方面。Costa在文献[5]中提出了基于多本体贝叶斯网络的OWL概率扩展语言(PROWL);Ding等在文献[6]中提出了一种基于标准的贝叶斯网络的OWL概率扩展语言Bayesowl,为OWL本体直接转换为贝叶斯网络提供了一系列的规则和流程,它支持本体内部、本体之间的推理,也支持贝叶斯网络推理;Volker和Hsuehleng在文献[7]中研究了对描述逻辑的扩展方法,该方法利用了概率和对OWL的依赖关系注释来表示贝叶斯网络中的不确定性信息。从以上研究可以看出,对本体进行概率扩展可以支持本体在不确定性知识上的表示与推理,为故障本体诊断方法的实现提供了依据。

本文主要通过增加本体语义,对Web本体语言进行概率扩展,制定了一系列的翻译规则和程序完成故障诊断知识本体到贝叶斯网络的结构转换,为不确定性推理提供诊断基础,然后设计基于概率约束的不确定性推理框架,制定详细的推理任务,并用实例进行验证,从而实现对矿井提升机故障诊断知识的不确定性推理研究。

1 贝叶斯网络模型与本体模型

1.1 本体贝叶斯网络形式化定义

从直观上讲,贝叶斯网络是一个有向无环图(directed acyclic graph,DAG),表现为一个赋值的因果关系网络图,网络中的每一个节点表示一个变量,各变量之间的弧表示事件发生的直接因果关系。贝叶斯网络应用于故障诊断,是把故障现象和故障原因作为网络节点,获得的征兆作为证据,通过历史数据的信息和诊断规则知识加以处理,根据节点间的因果关系和概率值可以推理出各种原因发生的后验概率,从而诊断推理出正确的结论[8]。为了将贝叶斯网络与本体知识有机结合,对其网络模型做形式化的定义。

定义1 贝叶斯网络模型的形式化定义为BN= {〈N,E〉,θ},其中,N为节点的集合,N中的每个节点都代表一个随机变量,因此每个节点都有一个概率分布;E为边的集合,这些边用来表示节点之间的影响关系;θ为一个条件概率表,用来指明节点之间的因果概率关系。

定义2 故障诊断本体O=(C,AC,R,AR,H,I, X),其中,C表示故障诊断概念集;AC表示每个概念的属性集;R表示概念之间的关系集;AR表示每个关系的属性集;H表示概念层次;I表示实例集;X表示公理集。

定义3 将上述两个定义有机结合,转换后的贝叶斯网络模型的可以形式化地表示为OBN={〈N, E〉,AC,X,I,θST},其中,概念节点集合N和边集合E组成贝叶斯网络模型的结构框架;AC表示概念节点的属性集合;X表示贝叶斯网络模型的公理集合;I表示概念节点的实例集合;θST表示概念节点的概率表集合。为方便描述,本文将转换后的贝叶斯网络模型称之为本体贝叶斯网络模型OBN。

1.2 本体模型的概率扩展

本体描述语言OWL作为一种知识表示方法,能够对特定领域的概念、术语及关系进行明确化、形式化的描述。概念的明确表示,使得本体推理结果也很明确,为了进行不确定性推理,需要对本体模型进行概率的扩展。

首先,对本体语言OWL增加额外的概率标注,在已构建好的本体中,将每个概念的概率信息以属性的方式附加到OWL本体中。根据贝叶斯网络的要求,这些概率信息包括先验概率、条件概率和后验概率等。先验概率是由以往的数据分析得到的,在无历史资料或历史资料不全的时候,凭主观经验来判断取得概率,用P(A)表示在没有训练数据前假设A拥有的初始概率,称为A的先验概率;在发生A的条件下,发生B的概率,称为条件概率,记做P(B|A)。机器学习中,关心的是P(A|B),即给定B时A成立的概率,称为A的后验概率,贝叶斯数据分析就是先验分布在经过了数据所提供的证据修订之后所形成的后验分布。

在提升机故障诊断本体中,先对故障本体附加对象属性hasProb表示概念有概率属性,数据类型属性hasPriorPr和hasCondPr属性来分别表示概念所具有的先验概率和条件概率属性,是一个浮点型数据。部分OWL代码如下所示:

2 本体模型到贝叶斯网络模型的转换

2.1 转换规则

2.1.1 概念与概念节点之间的转换

贝叶斯网络节点的确定,依赖于已经构建好的本体中的类。在本体结构转换为贝叶斯结构的过程中,节点的转换可通过以下几个规则[9－10]进行:

(1)将本体模型的概念集合C转换成OBN模型中的概念节点集合Nc,概念和概念节点之间的关系是一对一的映射关系。

(2)本体中域D定义的对象属性p,映射到贝叶斯网络的节点Np。

(3)本体中每个类的子类,映射到贝叶斯网络中为Nc的子节点SUB_Nc。

2.1.2 关系到边的转换

节点确定之后,就是本体结构中的关系到贝叶斯网络中边的转换,在本体OWL描述中,本体类之间的关系通过类公理和逻辑操作的构造函数进行描述,具体转换规则如下:

(1)构造函数“rdfs:subClassOf”。将本体模型的概念之间的上下位关系,在OWL中用标签＜rdfs:sub-ClassOf rdf:resource="#xxx"/＞表示上下位关系,即类与子类的关系,转换为OBN模型中边的集合Ec,并用两个节点之间的条件概率标识。

(2)通过对象属性限制的两个类C1和C2,他们之间的关系通过属性p相关联,在转换的OBN中,各节点之间的有向弧连接。

2.1.3 属性值、实例、公理的转换

(1)属性值的转换。

本体域中概念类的属性是通过本体限制提供的约束来完成的,包括对象属性和数据类型属性。其中本体模型中概念之间的非上下位关系R,通过对象属性体现,在本体OWL文件中,用标签＜owl:onProperty rdf:resource="xxx"/＞表示概念名为“xxx”的属性,转换成OBN概念节点的属性集Ep。

(2)实例的转换。

将本体模型中概念的实例集合I,在本体OWL文件中,用标签＜rdf:Description rdf:ID="xxx"＞来表示,转换成OBN模型概念节点的实例集合I。

(3)公理的转换。

将本体模型中公理的集合X转换成OBN模型中的公理集合X,在本体模型中,任何一个完整的OWL片段都可被看作是公理,用＜owl:xxx＞…＜/xxx＞来表示,它可被用来描述概念、属性和实例,所以公理转换的实现,可以通过概念、属性和实例的转换规则来实现。

至此,完成了本体模型到OBN模型的结构转换,不难发现,本体模型形式化定义中的各个元素,利用上述翻译规则,可以分别转换成OBN模型形式化定义中的元素,它们之间的对应关系是:Cfa→N,Hfa→E,AC→AC,X→X,Ifa→I,Rfa→θST。这也就证明了本文提出的本体模型到贝叶斯网络模型的转换规则是完备的。

2.2 条件概率表的构建

在本体中通过设置概率属性来表示不确定性的知识之后,在将本体模型和贝叶斯网络进行结构转换时,需要把这些概率信息也进行相应的转换,即建立每个节点的条件概率分布表(conditional probability table,CPT)。CPT表明了故障原因与故障现象之间的概率依赖关系,是处理故障诊断系统中不确定性知识的推理依据[11]。

2.2.1 先验概率的计算

在本文中,OBN模型的每个节点先验概率的计算方法是:用该概念节点所包含的实例数除以整个OBN模型所包含的实例数。这种方法的基本思想是概念的语义内容越丰富,它所包含的实例数就越多,这样对应的OBN模型中概念节点的出现的概率就越大。

2.2.2 条件概率的计算

根据1.2节对先验概率及条件概率的定义,设试验E的样本空间为S,A、B为E的事件,事件A发生的概率记为P(A),事件B发生的概率记为P(B),事件A和事件B同时出现的概率记为P(AB),在A已经发生的条件下,B发生的概率称为A发生的条件下B发生的条件概率,记为

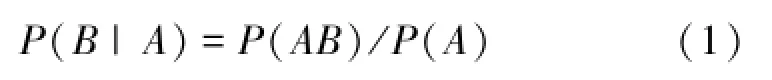
在OBN模型中,B和A分别表示OBN模型中的子概念节点和父概念节点,由于概念B是概念A的子概念,它们之间的语义包含关系为:B⊆A,或A∩B=B,那么P(AB)=P(B),因此OBN模型中条件概率公式可简写为

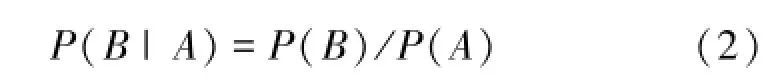
在得到这两个概念节点的先验概率后,利用式(2)计算OBN中节点之间边的条件概率,并形成相应的条件概率表。

依据以上算法,完成对OBN中各节点条件概率的计算,并构建相应的条件概率表。以提升机制动系统中空动时间过长的故障现象为例,该征兆的出现是由制动力矩不足的原因引起的,而引起制动力矩不足的子原因又有弹簧故障(spring fault)、闸瓦故障(break shoe fault)、油缸故障(cylinder fault)、残压过高(high residual voltage)等。要判定具体的故障原因,需要对闸瓦位移、弹簧力、闸瓦摩擦系数、液压站油压、左右偏摆量、提升速度、提升加速度等进行测量,由此构建贝叶斯网络如图1所示。

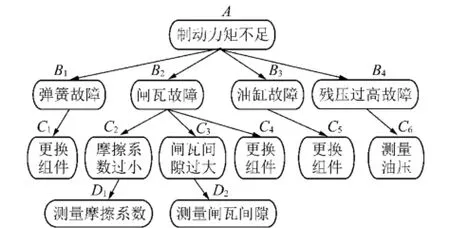
图1 贝叶斯网络构建Fig.1 Bayesian network construction

在样本学习和领域专家参与的情况下,计算先验概率。假设制动力矩不足的先验概率是0.2,依据以上规则对各节点的条件概率进行计算,并构建条件概率,如图2所示。

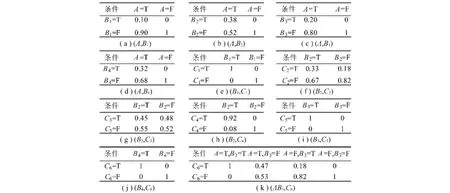
图2 引起制动力矩不足的条件概率Fig.2 CPTs of insufficient braking torque

3 提升机故障诊断不确定性知识融合推理方法

3.1 基于本体的贝叶斯网络的模型构建

本文使用基于本体的贝叶斯网络方法实现矿井提升机智能故障诊断系统中的不确定性知识的推理,实质上结合了本体和贝叶斯网络两种推理方式。本体推理是建立在描述逻辑之上,提供了基本的描述逻辑推理服务,用以完成对故障诊断知识进行语法、语义一致性的验证以及本体的解析,然后通过贝叶斯网络推理方法,借助Netica API贝叶斯网络可视化推理平台进行推理,构建集本体推理与贝叶斯网络推理于一体的融合推理模型。故障诊断框架如图3所示。

本文使用由惠普实验室开发的Java软件开发工具包Jena提供的OWLAPI读取本体信息,对语法进行检查;使用本体自带的推理机Pellet和本体解析工具Jena对本体进行语义验证及解析。

3.2 启发式故障诊断搜索树

概率推理和最大后验概率解释是贝叶斯网络推理的两个基本任务[12－13]。基于搜索的算法是将贝叶斯网络中需要计算的节点变量取值看作一个状态空间,运用启发式搜索在整个状态空间中对计算结果影响较大的状态,并用这些状态代替整个状态空间进行计算。在矿井提升机故障诊断领域,由于故障发生的概率较小,要求诊断推理的实时性强,这种情况采用基于搜索的方法最为适用。

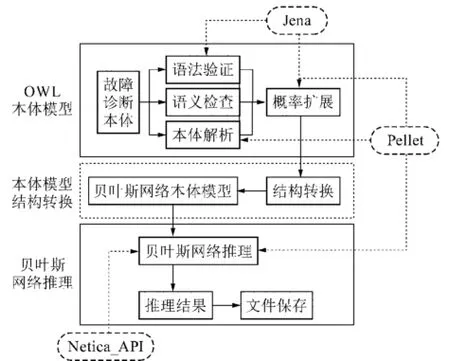
图3 基于贝叶斯网络和本体的故障诊断推理框架Fig.3 The inference framework of fault diagnosis based ontology and Bayesian network

在问题求解之前,首先定义状态和状态空间,由N个节点构成的所有有向无环图的集合,称为贝叶斯网空间[14－16]。本文中启发式搜索就是在状态空间中对每一个搜索的节点进行后验概率评估,选择概率值最高的状态节点,再从该节点进行搜索直到未考察到的叶节点的概率之和小于误差限定,找到目标状态为止[17]。本文按照上述搜索方法,从观察到的故障征兆集E={E1,E2,…,Em}开始,通过选择具有最大后验概率P(N)的故障节点,并对其进行检查,判定其运行的状态,并将结果加入证据集中进行下一轮的诊断,最终搜索到目标节点。以节点的概率估计函数作为搜索的启发函数f,算法描述如下:

(1)输入证据集E={E1,E2,…,Em},诊断集D= {Φ}。

(2)计算每个证据先验概率或后验概率P(E)。

(3)从证据集中选择具有最大后验概率的节点Ei。

(4)以Ei为初始状态,建立与Ei相关的故障节点N、故障诊断D和故障征兆E的状态空间,计算f(Ei)。

(5)按照原贝叶斯网络中节点之间的关系,建立以Ei为初始状态的搜索树。

(6)启发式搜索该搜索树。计算所有故障节点的后验概率P(N),与f(Ei)比较,删除多余节点;选择具有最大后验概率的故障节点进行诊断推理。

(7)若找到目标节点,则把该节点加入到诊断集D中,返回该节点的后验概率。

(8)若未找到目标节点,则返回步骤(3),从证据集中选择其他节点重复步骤。

4 矿井提升机故障诊断推理实例

以矿井提升机制动系统中的制动器故障为例,说明基于贝叶斯网络的提升机故障诊断本体的诊断推理过程。

实例1:空行程时间过长故障原因判定。

本文使用了贝叶斯网络的方法对矿井提升机故障诊断领域中的不确定知识进行诊断推理,因此对于某一故障现象,并不需要列出导致它产生的所有故障原因,只需要选取与现象最相关的事件子集来代替导致该现象出现的完备集合进行概率的计算。现如果只考虑故障现象与故障之间的因果关系,把故障现象节点均设为二元变量,即表示故障现象是否出现,可以得到故障现象与故障原因关系。对其进行贝叶斯网络结构的转换,得到的贝叶斯网络模型部分结构如图4所示,图中的每个节点对应图2中的一个条件概率。在矿井提升机故障中,制动器故障主要原因就是制动力矩过大或过小,图4中,空行程时间超限、制动缓慢、过卷、溜车等故障现象彼此独立,根据故障现象分析产生其的具体故障原因需要应用本文的推理方法。

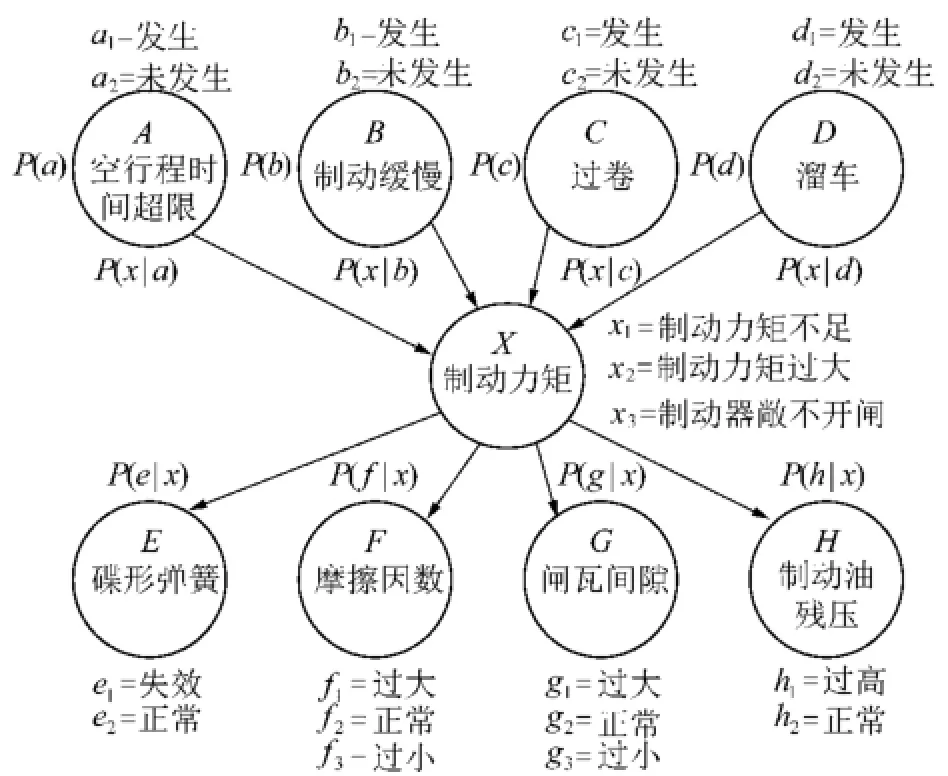
图4 转换后的贝叶基斯网络模型结构Fig.4 The transformed Bayesian network model structure

根据已建立的贝叶斯－本体故障诊断模型,利用Norsys公司提供的接口Netica API在贝叶斯网络推理平台上进行可视化推理,打开上述贝叶斯网络模型的OWL文件或者直接录入节点条件概率值,初始状态下,依据贝叶斯网络推理得到的结果如图5所示。

图5 贝叶斯网络推理结果Fig.5 The Bayesian network inference result

由现场监测得出,在整个制动过程中,出现了空行程时间过长(指在贴闸过程中,全松闸状态即闸瓦间隙最大状态到闸瓦间隙变为零(贴闸)的过程所花费的时间,《煤矿安全规程》规定空行程时间不得超过0.3 s)的现象,其它故障现象并未产生,引起空行程时间超限的直接原因是制动力矩不足,现加入证据及诊断规则。在实验前,对每个闸的弹簧预压缩量和弹簧刚度进行了测试和调换,使其都达到了规定标准,故排除弹簧故障。由贝叶斯网络推理得到的结果如图6所示。

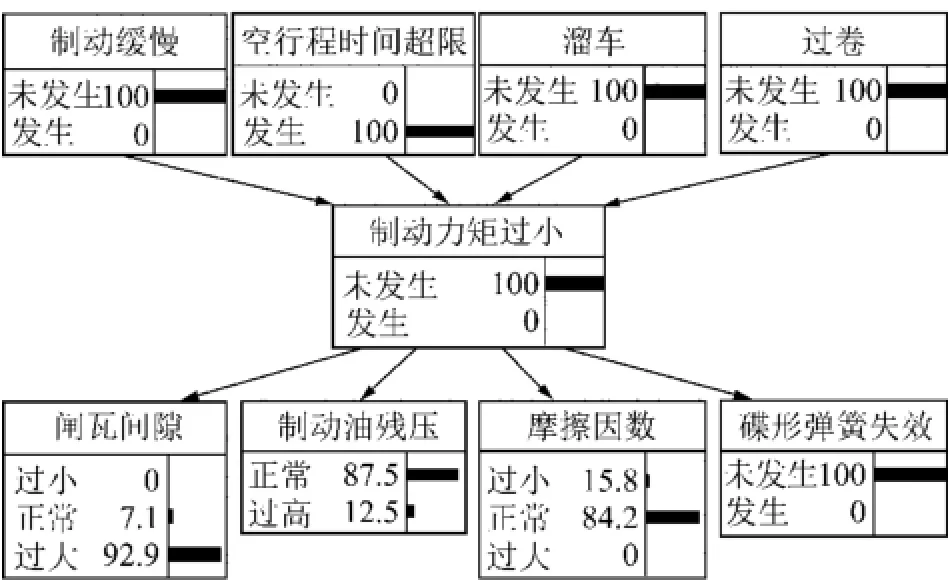
图6 加入证据的贝叶斯网络推理结果Fig.6 The Bayesian network inference result with evidences

由此可知,闸瓦间隙过大引起的制动力矩过小的可能性大,为了验证该结果的正确性,根据监测数据做如下分析:

在提升机运行过程中,摩擦因数在正常范围内(＜0.4);绘制制动油压曲线如图7所示,该图表明制动过程中制动油残压值在正常范围(＜0.5 MPa)内;绘制闸瓦位移曲线如图8所示,从图中可以看出,闸瓦间隙超限(＞2 mm),由此可判定该故障为闸瓦间隙过大引发的空行程时间超限故障,与上述推理结果完全相符,需要对闸瓦间隙进行调整。

实例2:制动时间过长故障的原因判定。

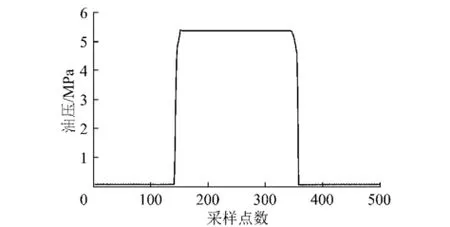
图7 制动油油压曲线Fig.7 The brake oil pressure curve

图8 闸瓦位移曲线Fig.8 Brake shoe displacement curve

在提升机运行的过程中,根据监测数据曲线显示,表明出现了制动时间过长的故障现象,由本文中的推理方法,根据上述推理过程,得出其故障原因概率最大值为0.87,对应的故障原因为制动液压缸卡缸,下面对该诊断结论进行验证。实验过程中,在提升机爬行阶段结束后,利用制动器进行减速的阶段即由爬行速度减为零的这个过程所用时间过长,减速度值偏小,表明出现了制动时间过长的现象。从4号闸的闸瓦位移曲线(图9)可看出在贴闸过程中,它所花费的时间明显大于其他各闸,并且中间有一些采样点值保持不变。绘制油压曲线如图10所示,从图中可以看出残压不高。结合图9和图10可得出在贴闸过程中,当油压不断变化时,有一段时间4号闸的位移值不发生变化,符合卡缸故障的故障机理。

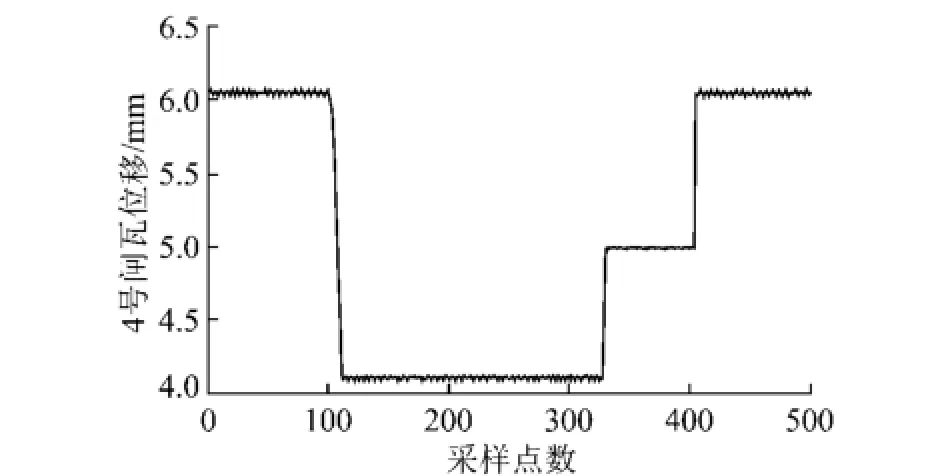
图9 4号闸闸瓦位移曲线Fig.9 Brake shoe displacement of number 4 brake

上述两个实例表明,本文提出的提升机故障诊断不确定性推理方法具有良好的适应性。推理结果文件可直接保存成Hoist diagnosis.neta,供Java程序直接调用,完成提升机故障诊断系统的诊断推理功能。

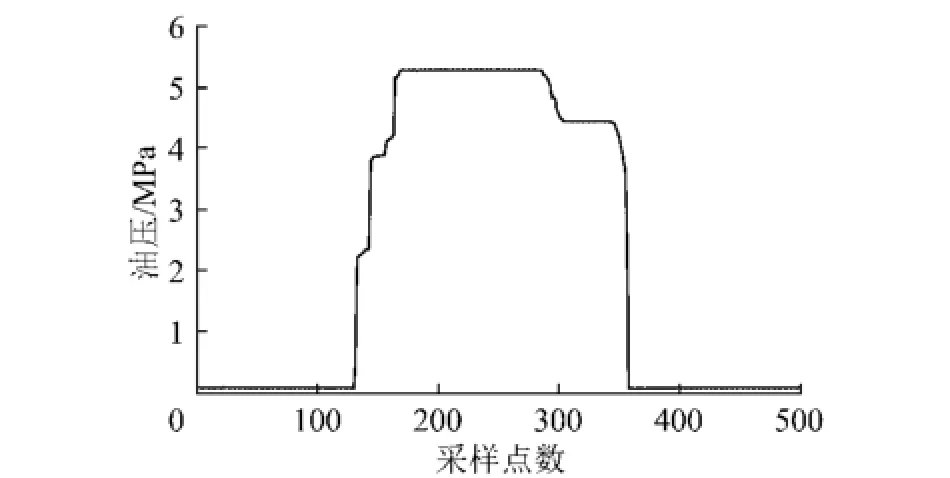
图10 液压站油压曲线Fig.10 Oil pressure of hydraulic station

5 结 论

(1)分析了本体模型与贝叶斯网络的基本结构和原理,对本体贝叶斯网络OBN做了形式化的定义,然后以贝叶斯网络为概率模型,对本体语言OWL的概率扩展进行了深入研究。

(2)制定了本体模型到贝叶斯网络模型转换的一系列翻译规则,给出了先验概率、条件概率的计算方法,完成了各节点条件概率表的计算。

(3)建立了基于本体的贝叶斯网络推理模型,对本体推理和贝叶斯推理的方法分别进行了详细的研究,提出了二者结合的故障诊断融合推理模式。

(4)针对矿井提升机故障诊断推理的要求,提出了基于启发式故障搜索树的推理策略,给出了提升机故障诊断的详细诊断推理过程。

(5)以矿井提升机制动系统中的制动器故障为例,说明基于贝叶斯网络的提升机故障诊断本体的诊断推理过程,并进行了正确性的检验。经验证,该融合推理模型处理所得的诊断结果具有较高的可信度。

[1] Du Ning,Huang Dao.Ontlolgy-based fault diagnosis for chemical process[J].Computer Integrated Manufacturing Systems,2005, 11(4):587－591.

[2] 周安美,于德介,吴雪明,等.基于本体的大型风力发电机组故障智能诊断研究[J].中国机械工程,2012,23(17):2075－2080.

Zhou Anmei,Yu Dejie,Wu Xueming,et al.Research on intelligent fault diagnosis for large-scale wind turbines based on ontology[J].China Mechanical Engineering,2012,23(17):2075－2080.

[3] Chen Guorong,Yan Ping,Yan Hua,et al.Empirical analysis on blast furnace fault diagnosis method based on ontology[J].Journal of Chongqing University,2012,35(5):35－39.

[4] Bi Zhongwei,Zhang Ming,Jin Feng,et al.Study on the prior information quantity and fusion technology applied in inference of rock mechanics parameters with Bayes method[J].Journal of the China Railway Society,2011,33(2):96－100.

[5] Costa P C G,Laskey K B,Laskey K J.PR-OWL:A bayesian ontology language for the semantic web[J].Lecture Notes in Computer Science,2008,5327 LNAI:88－107.

[6] Ding Z,Peng Y,Pan R.BayesOWL:Uncertainty modeling in semantic web ontologies[J].Studies in Fuzziness and Soft Computing, 2006,204:3－30.

[7] Haarslev Volker,Pai Hsuehleng,Shiri,et al.Uncertainty reasoning for ontologies with General TBoxes in description logic[J].Lecture Notes in Computer Science,2008,5327 LNAI:385－402.

[8] Zeng Yihui,E Jiaqiang,Hua Hao,et al.Fault diagnosis on cooling system of ship diesel engine based on Bayes network classifier[J].Journal of Central South University,2010,41(4):1379－1384.

[9] 杨喜权,曹雪亚,国頔娜,等.基于贝叶斯网络的本体不确定性推理[J].计算机应用,2008,28(5):1170－1173.

Yang Xiquan,Cao Xueya,Guo Dina,et al.Reasearch of ontology uncertainty reasoning based on Bayesian network[J].Journal of Computer Applications,2008,28(5):1170－1173.

[10] Fenz,Stefan.An ontology-based approach for constructing Bayesian

networks[J].Data and Knowledge Engineering,2012,73:73－88.[11] Song Qijiang,Xu Minqiang,Wang Rixin.Fault diagnosis approach

based on fuzzy probability SDG model and reasoning[J].Control and Decision,2009,24(5):692－696.

[12] Dlamini,Wisdom M.A Bayesian belief network analysis of factors influencing wildfire occurrence in Swaziland[J].Environmental Modelling and Software,2010,25(2):199－208.

[13] Cai Baoping,Liu Yonghong,Fan Qian,et al.Application of Bayesian networks to reliability evaluation of software system for subsea blowout preventers[J].International Journal of Control and Automation,2013,6(1):47－60.

[14] Cheng J,Greiner R,Kelly J,et al.Learning Bayesian Net-works from data:an information-theory based approach[J].Artificial Intelligence,2002,137(1－2):43－90.

[15] Wang Fei,Liu Dayou,Wang Songxin.Research on incre-mental learning of bayesian network structure based on genetic algorithms [J].Computer Research and Development,2005,42(9):1461－1466.

[16] Melancon G,Dutour I,Bousquet-Melou M.Random generation of directed acyclic graphs[J].Electronic Notes in Discrete Mathematics,2001,16(10):202－207.

[17] Xin Junchang,Huang Jianmei,Wang Guoren,et al.An uncertain skyline query algorithm based on state space searching[J].Journal of Northeastern University,2008,31(3):338－341.

An uncertain reasoning method of hoist fault diagnosis

LI Juan-li,YANG Zhao-jian

(College of Mechanical Engineering,Taiyuan University of Technology,Taiyuan 030024,China)

Aiming to the uncertainty problem in hoist fault diagnosis process,a new fault diagnosis uncertainty knowledge reasoning method was proposed,which based on ontology and Bayesian.The method extended the uncertainty representation of ontology for domain knowledge by using OWL language,finished the conversion from ontology structure to Bayesian network through a series of translation rules and procedures;then,it constructed the fusion reasoning model based on ontology and the Bayesian network.The model checked the grammar and verified the semantic consistency of fault diagnosis ontology knowledge using ontology reasoning,and then it inferenced uncertainty by Bayesian network based on the heuristic search tree;finally it test on the Bayesian network visualization reasoning platform Netica.The mine hoist braking system fault diagnosis example shows that the fusion reasoning model has better ability of fault recognition and the diagnosis results have higher credibility.

Bayesian network;ontology;hoist;fault diagnosis;uncertain reasoning

TD444

A

0253－9993(2014)03－0586－07

李娟莉,杨兆建.提升机故障诊断不确定性推理方法[J].煤炭学报,2014,39(3):586－592.

10.13225/j.cnki.jccs.2013.1179

Li Juanli,Yang Zhaojian.An uncertain reasoning method of hoist fault diagnosis[J].Journal of China Coal Society,2014,39(3):586－592.doi:10.13225/j.cnki.jccs.2013.1179

2013－08－19 责任编辑:许书阁

山西省科技重大专项资助项目(20111101040)

李娟莉(1979—),女,山西寿阳人,讲师,博士。Tel:0351－6010414,E－mail:lijuanli@tyut.edu.cn。通讯作者:杨兆建(1955—),男,河北高阳人,教授,博士生导师。Tel:0351－6010404,E－mail:yangzhaojian@tyut.edu.cn