基于SPH的煤岩单轴加载声发射数值模拟
孙超群,程国强,李术才,李利平,3,许振浩,郭 明,林 鹏
(1.山东大学岩土与结构工程研究中心,山东济南 250061;2.山东科技大学矿山灾害预防控制实验室,山东青岛 266590;3.国土资源部煤炭资源勘查与综合利用重点实验室,陕西西安 710054)
基于SPH的煤岩单轴加载声发射数值模拟
孙超群1,2,3,程国强2,李术才1,李利平1,3,许振浩1,郭 明1,林 鹏1
(1.山东大学岩土与结构工程研究中心,山东济南 250061;2.山东科技大学矿山灾害预防控制实验室,山东青岛 266590;3.国土资源部煤炭资源勘查与综合利用重点实验室,陕西西安 710054)
基于SPH(光滑粒子流体动力学)数值计算方法,研究了非均质煤岩材料的单轴压缩试验声发射效应,揭示了煤岩的声发射效应随着均质度m的变化规律。研究表明:随着均质度m值的增大,试件的声发射效应由群震型逐渐变为前震—主震—余震型、主震型;试件积聚能量的能力逐渐增强,材料属性由理想弹塑性材料向极端脆性材料转变,破坏模式由塑性流动破坏逐渐变为脆性破坏,其破坏形式越来越剧烈。
SPH;声发射;均质度;单轴加载
SPH(smoothed particle hydrodynamic method,简称SPH方法或光滑粒子法)是一种无网格的粒子方法,最早是由Lucy[1]、Gingold和Monaghan[2]提出,最先用于无边界的天体物理学数值模拟研究[3-4]。SPH方法是一种求解高度非线性动力学问题的数值方法,在20世纪90年代得到飞速发展。目前,SPH方法已经被广泛的应用到流体和固体的数值模拟计算中来。在流体模拟方面,光滑粒子法被应用到自由表面流[5-6]、多孔介质流[7-8]、两相和多相流[9-10]、湍流[11]等问题的模拟。在固体力学方面,光滑粒子法最主要是应用于超高速冲击研究[12-15]、高速侵彻问题[16-17]以及高能炸药爆轰[18-19]和水下爆炸[20-21]等。 此外,光滑粒子法还被用于金属成型[22-23]、材料的切削加工[24-25]等问题的模拟。光滑粒子法在各种问题上的应用使得许多方面的研究得到了改进与完善。但目前该方法在岩石力学中应用尚少,其应用前景将十分广阔。
1 SPH方法的基本原理
1.1 SPH的基本思想
光滑粒子流体动力学(SPH)方法是一种拉格朗日形式的无网格粒子法。该方法将求解的问题使用一系列有限数量的离散化粒子来描述,利用核函数近似法求解含有时间导数的微分方程,从而解决数值分析问题。
SPH方法的核心思想中最重要的2个思想就是无网格性质与核近似法[26]:
(1)SPH方法求解的问题时,问题域是用一系列任意分布且无任何连接的粒子来表示的,这决定了SPH方法的无网格性质。
(2)SPH方法中用积分表示法来近似场函数,利用积分法的光滑作用,来保持弱形式方程的数值稳定。这种方法就称为核近似法。
SPH方法中的核函数一般被理解为一种权函数。核函数在SPH方法中是非常重要的,它不但决定了函数近似式的形式、定义粒子支持域的大小,而且还决定了SPH核近似和粒子近似的一致性和精度。目前,国内外主要用到的光滑函数有以下几种:钟形函数、高斯型核函数、三次样条函数(B-样条函数)、四次样条函数、五次样条函数[26]。到目前为止,三次样条函数是现有SPH文献中应用最为广泛的光滑函数,在本文的SPH模拟中,也使用了三次样条函数。三次样条函数表达式[26]如下:

式中,αd在一维、二维和三维空间中分别为为两个粒子间距离;h为光滑长度。
1.2 具有材料特性的SPH基本方程
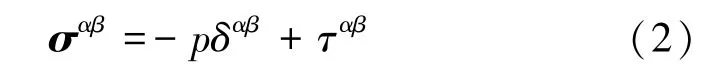
式中,p为各向同性压力或球应力;τ为黏性剪切应力或偏应力;δ为狄拉克符号;α,β为张量指标,取1,2, 3。
在固体力学中,其模型一般允许应力为应变和应变率的函数。在小变形假设下,应力率与应变率互成比例,比例系数为剪切模量。

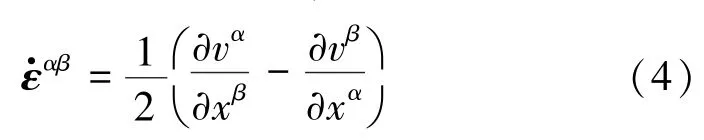
其中,v为粒子的速度;x为粒子的位置。
应变率张量的SPH离散格式为

式中,mj为粒子j的质量;ρj为粒子j的密度;为所用核函数。
利用塑性增量理论,将弹塑性材料的应变率写成2部分:一部分为弹性应变率,另一部分为塑性应变率,即
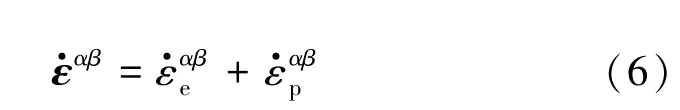
根据广义虎克定律,弹性部分为

由塑性流动法则,塑性应变部分为
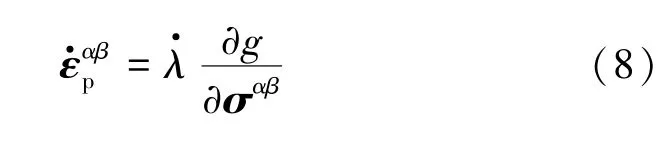
将式(6)和(7)代入式(8)中,引入Jaumman应力率以处理大变形,可得到粒子i的本构关系,即



材料的各向同性压力p[27]可采用如下形式:

式中,K为材料的体积模量;ρ0为参考密度。
声速采用Hallqusit在提出的表达式[27]:
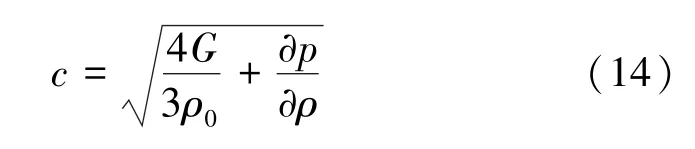
2 数值计算模型
本文采用SPH方法来模拟煤岩试件单轴加载试验,这是一次崭新的尝试。应用SPH方法自主研发程序,对煤的单轴加载试验进行数值模拟。
2.1 本构关系模型
岩石材料具有非均质性,其具体破坏形态千差万别,考虑试件的破坏必然发轫于内部细观破坏,进而破坏发展、积累,表现出宏观上变性破坏形态。对于细观上的单个粒子来说,其物理力学性质未必如此复杂,所以假设数值实验中的所有粒子符合统一的本构关系,惟一的差别在于非均匀分布的物理量,从这两点出发,只需要粒子屈服的数量和程度不同,在宏观上能够展现出多样的破坏状态。所以在本文的SPH模拟中,综合岩石的力学性质基本特征,引入如下假设:①组成宏观岩石的细观介质是弹-脆-塑性介质(图1);②物理参数具有非均匀性,并且假定其服从Weibull分布[28];③裂缝的扩展及介质的破坏是一个准静态过程。

图1 数值模拟粒子模型本构关系Fig.1 Particle constitutive relation model in numerical simulation
采用的粒子本构模型体现了材料的弹性、脆性和塑性。考虑煤岩是非均质的材料,文中采用Weibull分布的方法来描述材料的非均质情况。假定煤岩体弹性模量与黏聚力均符合Weibull分布,则用均质度系数m描述其非均质性。

材料的屈服准则采用Drucker-Prager准则,当满足式(15)时,开始产生塑性变形,即
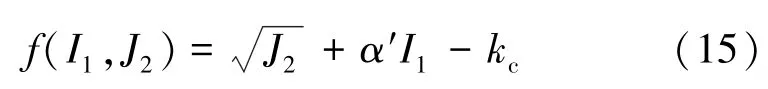
其中,I1和J2分别为第1和第2应力张量不变量;α′和kc是常数,它们仅与岩石的黏聚力c和内摩擦角φ有关,

Drucker-Prager准则考虑了中间主应力的影响,又考虑了静水压力的作用,克服了Mohr-Coulomb准则的主要弱点,可解释岩土材料在静水压力下也能屈服和破坏的现象。
2.2 数值计算模型
本次数值计算采用二平模型,模型几何尺寸为5 cm×10 cm,模型离散为3 200个实粒子。计算步长为1×10-8s,上端加载,下端固定;模型中煤岩试件弹性模量的期望值均为2.03 GPa,泊松比均为0.36,内摩擦角均为30°,屈服强度的期望值均为1 MPa,残余强度为屈服强度的1/4;采用D-P屈服准则,计算过程不考虑形状效应影响,均质度分别取m=1.1,2,4, 6。分布形态如图2所示。

图2 粒子计算模型Fig.2 Calculation model of particles
3 模拟结果及分析
3.1 数值计算结果分析
在SPH数值程序中,加入了对试件中粒子声发射情况的计算程序。在单轴压缩试验的过程中,将达到屈服极限以及发生破坏的粒子在破坏的瞬间视为一次声发射发生,这样可以清楚地记录试件在压缩过程中粒子发生声发射的情况。通过声发射信息,可以清楚的看到试件在单轴压缩过程中,试件中粒子发生屈服破坏的情况。图3记录了不同均质度m下单轴压缩过程中的声发射情况。
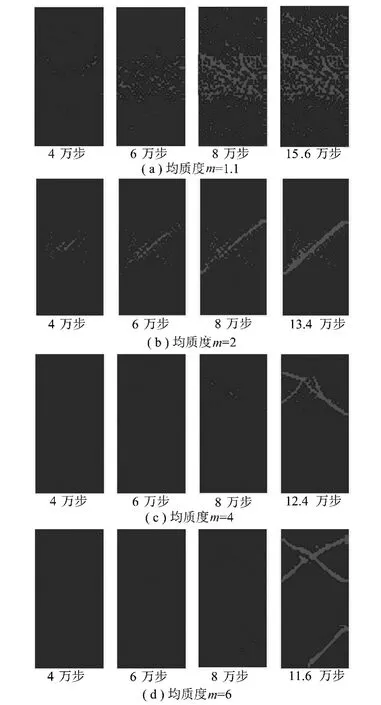
图3 试件压缩过程粒子声发射变化Fig.3 AE nephogram of specimen during compressing
总体来看,当均质度m=1.1时,试件的均质程度较低,粒子物理量较分散,在压缩过程中不断有粒子屈服破坏而产生声发射现象;随着m的增大,试件在压缩前期声发射的数量逐渐减少,在压缩试验后期,会在较短时间内爆发出大量声发射信号。
通过记录在加载过程应力、声发射数随加载步变化规律等中,绘制出试件的声发射信息统计柱状图如图4所示。
根据文献[29-30]中所描述,声发射的模式主要表现为3种模式:群震型、前震—主震—余震型、主震型。根据以上结果可以看出:当试件均质度m较小时(m=1.1,2),在试验加载初期,煤岩试件中就有少量的声发射出现;随着加载的继续进行,声发射数目逐渐增多,但是总体来讲声发射数没有特别显著的急剧增加,虽然在接近煤岩屈服强度的时候有几次高峰值,但是其数量仍相对较低,主震和余震不容易分开,声发射累计曲线无明显的突升现象,这种声发射模式属于群震型。当试件均质度m增大时(m=4),加载初期声发射数极少,随着加载持续进行一段时间后,声发射数开始增加,在达到其极限强度前随着试件的主破裂发生,声发射数相对较高,有相对明显的主震发生,但在主破裂发生后,声发射数又相对减少很多;声发射累计曲线有一小段明显的突升现象,这种声发射的模式属于前震—主震—余震型。当试件均质度m继续增大时(m=6),加载初期与主破坏之后基本没有声发射或仅有零星的声发射现象,但是在主破坏发生即应力曲线有急剧的跌落现象出现时,声发射数有非常显著的增加,声发射累计曲线有明显的突跃现象,这种声发射模式属于主震型。
根据应力-加载步以及声发射累计曲线可以得出:试件破坏过程中,当质度m较低时,试件材料接近于理想弹塑性材料,其声发射模式为群震型,该类型材料不具有冲击倾向性;随着均质度m的增大,试件材料渐变为软化材料,其声发射模式为前震-主震-余震型,此种类型材料会具有一定的冲击倾向性;当均质度m增大到一定值,试件材料将接近于极端脆性材料的试件,其声发射模式为主震型,此种类型材料会具有较强的冲击倾向性。这也与文献[31]中所述理论相一致。
3.2 计算结果能量分析
岩石类材料的变形破坏过程就是能量耗散和能量释放的过程。试件破坏时有大量的能量释放出来,声发射仅是其中的一种能量形式。声发射数的多少也从另一个方面反映了试件破坏的瞬间所释放出的能量的多少[32-35]。
根据加载过程应力、声发射数随加载步变化曲线的一致性可以得出:当均质度m较小时,极限强度前的声发射累计数比较大,即声发射累计能量也较大,这表明其变形能积聚阶段损失的能量也比较多,试件积聚弹性变形能的能力较差,试件变形破坏以塑性流动破坏为主。随着均质度m的增大,极限强度前的声发射累计数逐渐变小,即声发射累计能量也随之变小,这表明其变形能积聚阶段损失的能量也正逐渐减小,试件积聚弹性变形能的能力逐渐增强,试件主要变形破坏由塑性流动破坏向脆性破坏转变。当均质度m较大时,极限强度前的声发射累计数非常小,即声发射累计能量也非常小,这表明试件在达到屈服强度之前弹性变形能的损失的能量也非常少,试件积聚弹性变形能的能力较强,其破坏形式为脆性破坏为主。
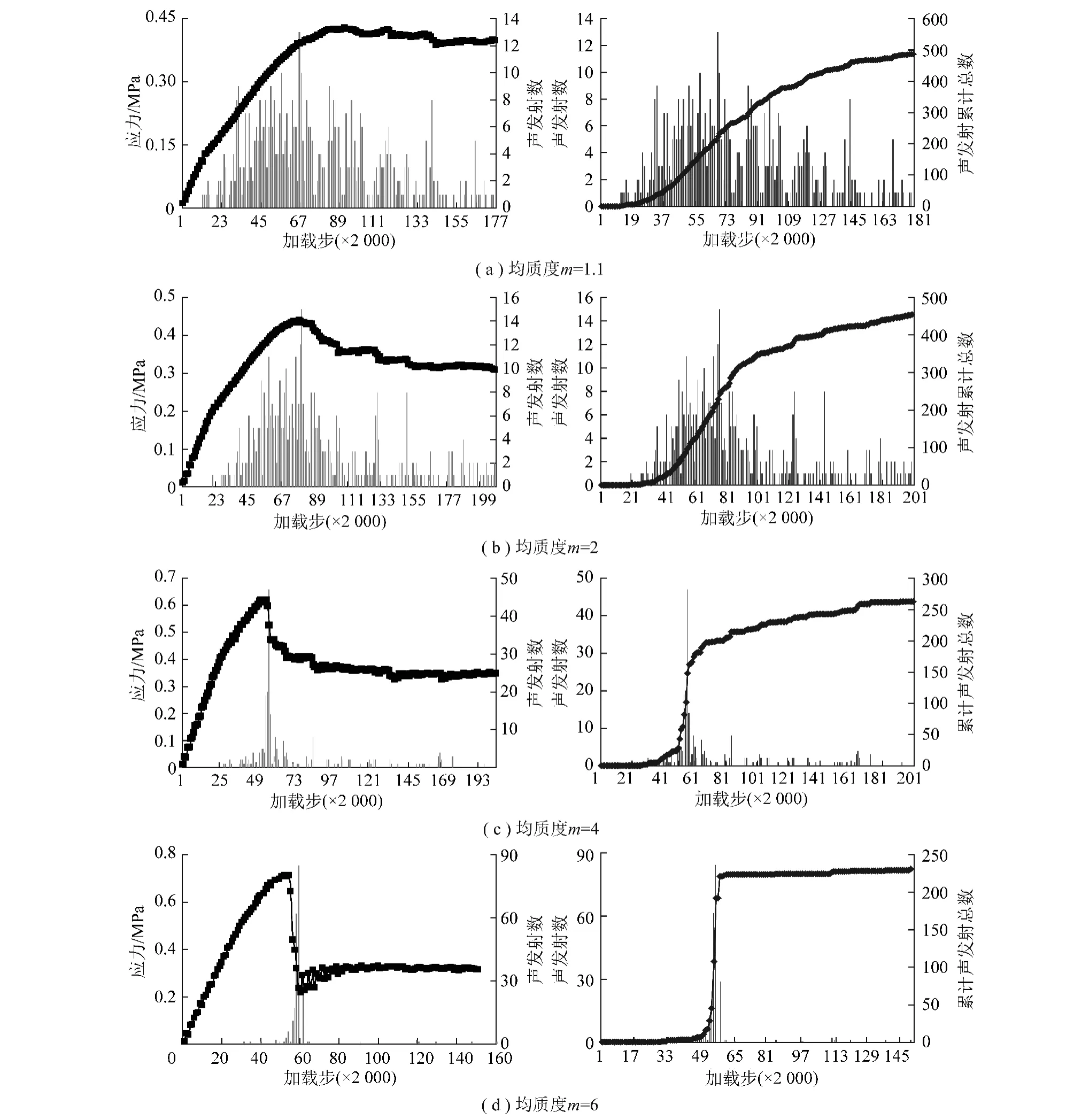
图4 试件加载过程声发射柱状Fig.4 Histograms of AE number-step of specimen
由此可以得出,煤试件积聚弹性变性能的能力随着均质度m的增大而增强;试件的变形破坏模式由塑性流动破坏逐渐变为脆性破坏,其破坏形式越来越剧烈。
4 结 论
(1)基于SPH方法对岩石类材料单轴压缩试验进行了数值模拟。通过不同非均质度试件的声发射震型分析,得出了平面模型下的声发射模式:
①当试件均质度m=1.1,2时,试件的声发射模式群震型;②当试件均质度m=4时,声发射的模式属于前震—主震—余震型;③ 当试件均质度m=6时,声发射模式属于主震型。
(2)应力-加载步曲线与声发射累计曲线结果分析表明:
①试件破坏过程中,均质度m较小时,试件接近于理想弹塑性材料,其声发射模式为群震型;②随着均质度m的增大,试件材料渐变为软化材料,其声发射模式为前震—主震—余震型;③当均质度m增大到一定值,试件材料将接近于极端脆性材料,其声发射模式为主震型,此种类型材料具有较强的冲击倾向性。
(3)能量分析表明:随着均质度m的逐渐增大,试件积聚能量的能力逐渐增强,试件主要破坏模式由塑性流动破坏逐渐变为脆性破坏,破坏形式越来越剧烈。
[1] Lucy L B.A numerical approach to the testing of the fission hypothesis[J].Astronomical Journal,1977,82(12):1013-1024.
[2] Gingold R A,Monaghan J J.Smoothed particle hydrodynamics:Theory and application to non-spherical stars[J].Monthly Notices of the Royal Astronomical Society,1977,181(2):375-389.
[3] Gingold R A,Monaghan J J.Binary fission in damped rotating polytropes[J].Monthly Notices of the Royal Astronomical Society,1978, 184(2):481-499.
[4] Gingold R A,Monaghan J J.A numerical study of the Roche and Darwin problems for polytropic stars[J].Monthly Notices of the Royal Astronomical Society,1979,188:45-58.
[5] Monaghan J J.Simulating free surface flows with SPH[J].Journal of Computer Physics,1994,110(2):399-406.
[6] Ferrari A,Dumbser M,Toro E F,et al.A new 3D parallel SPH scheme for free surface flows[J].Computers&Fluids,2009,38 (6):1203-1217.
[7] Zhu Y,Fox P J,Morris J P.A pore-scale numerical model for flow through porous media[J].International Journal for Numerical and Analytical Methods in Geo-mechanics,1999,23(9):881-904.
[8] Pereira G G,Prakash M,Cleary P W.SPH modelling of fluid at the grain level in a porous medium[J].Applied Mathematical Modelling,2011,35(4):1666-1675.
[9] Monaghan J J,Kocharyan A.SPH simulation of multi-phase flow [J].Computer Physics Communications,1995,87(1-2):225-235.
[10] Valizadeh A,Shaficefar M,Monaghan J J,et al.Modeling two-phase flows using SPH method[J].Journal of Applied Sciences,2008,8 (21):3817-3826.
[11] Monaghan J J.SPH compressible turbulence[J].Monthly Notice of the Royal Astronomical Society,2002,335(3):843-852.
[12] Hayhurst C,Clegg R A.Cylindrically symmetric SPH simulations of hypervelocity impacts on thin plates[J].International Journal of Impact Engineering,1997,20(1-5):337-348.
[13] 管公顺,张 伟,庞宝君,等.铝球弹丸高速正撞击薄铝板穿孔研究[J].高压物理学报,2005,19(2):132-138.Guan Gongshun,Zhang Wei,Pang Baojun,et al.A study of penetration hole diameter in thin Al-plate by hypervelocity impact of alspheres[J].Chinese Journal of High Pressure Physics,2005,19 (2):132-138.
[14] 贾 斌,马志涛,庞宝君.含泡沫铝防护结构的超高速撞击数值模拟研究[J].高压物理学报,2009,23(6):453-459.
Jia Bin,Ma Zhitao,Pang Baojun.Numerical simulation investigation in hypervelocity impact on shield structure containing aluminum foam[J].Chinese Journal of High Pressure Physics,2009,23(6): 453-459.
[15] 徐金中,汤文辉,徐志宏.超高速碰撞碎片云特征的SPH方法数值分析[J].高压物理学报,2008,22(4):377-383.
Xu Jinzhong,Tang Wenhui,Xu Zhihong.Numerical analysis of the characteristics of debris clouds produced by hypervelocity impacts using SPH method[J].Chinese Journal of High Pressure Physics,2008,22(4):377-383.
[16] Seo S,Min O,Lee J.Application of an improved contact algorithm for penetration analysis in SPH[J].International Journal of Impact Engineering,2008,35(6):578-588.
[17] 张 伟,胡德安,韩 旭.弹体侵彻运动陶瓷/金属复合装甲SPH模拟[J].固体力学学报,2010,31(S1):70-75.
Zhang Wei,Hu Dean,Han Xu.Simulation on projectile penetrating into moving ceramic/metal composite armor using SPH method [J].Chinese Journal of Solid Mechanics,2010,31(S1):70-75.
[18] Liu M B,Liu G R,Zong Z,et al.Computer simulation of high explosive explosion using smoothed particle hydrodynamics methodology[J].Computers&Fluids,2003,32(3):305-322.
[19] 强洪夫,王坤鹏,高巍然.基于完全变光滑长度SPH方法的高能炸药爆轰过程数值试验[J].含能材料,2009,17(1):27-31.
Qiang Hongfu,Wang Kunpeng,Gao Weiran.Numerical simulation of high explosive detonation process using SPH method with fully variable smoothing lengths[J].Chinese Journal of Energetic Materials,2009,17(1):27-31.
[20] Swegle J W,Attaway S W.On the feasibility of using smoothed particle hydrodynamics for underwater explosion[J].Computational Mechanics,1995,17(3):151-168.
[21] Liu M B,Liu G R,Zong Z,et al.Smoothed particle hydrodynamics for numerical simulation of underwater explosions[J].Computational Mechanics,2003,30(2):106-118.
[22] Bonet J,Kulasegaram S.Correction and stabilization of smooth particle hydrodynamics methods with applications in metal forming simulations[J].International Journal for Numerical Method in Engineering,2000,47(6):1189-1214.
[23] Cleary P W,Prakash M,Ha J.Novel applications of smoothed particle hydrodynamics(SPH)in metal forming[J].Journal of Materials Processing Technology,2006,177(1-3):41-48.
[24] Heinstein M,Segalman D.Simulation of orthogonal cutting with smoothed particle hydrodynamics[R].Report No.SAND97-1961,Sandia National Laboratoties,1997.
[25] Limido J,Espinosa C,Salaun M,et al.A new approach of high speed cutting modelling:SPH method[J].Journal of Physics IV, 2006,134(1):1195-1200.
[26] Liu G R,Liu M B.Smoothed particle hydrodynamic-a meshfree particle method[M].New Tersey:World Scientific Publishing Compa-ny,2003.
[27] Hallquist J O.LS-DYNA theoretical manual[R].California:Livermore Software Technology Corporation,1998.
[28] Krajcinovic D,Silva M A G.Statistical aspects of the continuous damage theory[J].Int.J.Solids Structures,1982,18(7):551-562.
[29] 梁正召,唐春安,黄明利,等.岩石破裂过程中声发射模式的数值模拟[J].东北大学学报(自然科学版),2002,23(10):1008-1011.
Liang Zhengzhao,Tang Chun’an,Huang Mingli,et al.Numerical simulation of patterns of acoustic emission in rock failure process [J].Journal of Northeastern University(Natural Science),2002, 23(10):1008-1011.
[30] 王学滨.不同强度岩石的破坏过程及声发射数值模拟[J].北京科技大学学报,2008,30(8):837-843.
Wang Xuebin.Numerical simulation of failure processes and acoustic emissions of rock specimens with different strengths[J].Journal of University of Science and Technology Beijing,2008,30(8): 837-843.
[31] 冯增朝,赵阳升.岩石非均质性与冲击倾向的相关规律研究[J].岩石力学与工程学报,2003,22(11):1863-1865.
Feng Zengchao,Zhao Yangsheng.Correlativity of rock inhomogeneity and rock burst trend[J].Chinese Journal of Rock Mechanics and Engineering,2003,22(11):1863-1865.
[32] 郭建卿,苏承东.不同煤试样冲击倾向性试验结果分析[J].煤炭学报,2009,34(7):897-902.
Guo Jianqing,Su Chengdong.Analysis on experimental results of rock burst tendency of different coal samples[J].Journal of China Coal Society,2009,34(7):897-902.
[33] 曹树刚,刘延保,张立强,等.突出煤体单轴压缩和蠕变状态下的声发射对比试验[J].煤炭学报,2007,32(12):1264-1268.
Cao Shugang,Liu Yanbao,Zhang Liqiang,et al.Experiment on acoustic emission of outburst-hazardous coal under uniaxial compression and creep[J].Journal of China Coal Society,2007,32 (12):1264-1268.
[34] 刘保县,赵宝云,姜永东.单轴压缩煤岩变形损伤及声发射特性研究[J].地下空间与工程学报,2007,3(4):647-650.
Liu Baoxian,Zhao Baoyun,Jiang Yongdong.Study of deformation damage and acoustic emission character of coal rock under uniaxial compression[J].Chinese Journal of Underground Space and Engineering,2007,3(4):647-650.
[35] 潘结南.煤岩单轴压缩变形破坏机制及与其冲击倾向性的关系[J].煤矿安全,2006(8):1-4.
Pan Jienan.Relationship between deformation&failure of coal and its burst potential under uniaxial compression[J].Safety in Coal Mines,2006(8):1-4.
《煤炭学报》2篇优秀论文入选“2013年中国百篇最具影响国内学术论文”
根据科技部中国科学技术信息研究所“2014年中国科技论文统计结果发布会”发布的信息,《煤炭学报》刊登的2篇论文入选“2013年中国百篇最具影响国内学术论文”,分别是:
(1)袁 亮.卸压开采抽采瓦斯理论及煤与瓦斯共采技术体系[J].煤炭学报,2009,34(1):1-8.
(2)谢和平,周宏伟,刘建锋,等.不同开采条件下采动力学行为研究[J].煤炭学报,2011,36(7):1067-1074.
“中国百篇最具影响国内学术论文”是从数百万计的论文中选出的,主要考察论文的创新性、论文的文献类型、是否前沿重点学科、论文发表的期刊水平、论文的规范化程度、论文他引率等,评选出的百篇论文代表了各个学科科研成果的最高水平。本年度公布的“2013年中国百篇最具影响国内学术论文”,按照学科部类划分,工业技术46篇、医药卫生16篇、基础科学25篇、农林牧渔12篇、管理及其他1篇。
“中国百篇最具影响国内学术论文”评选活动影响巨大,各单位更是将其视为代表科研实力的重要荣誉。《煤炭学报》在2013年度有2篇论文入选,充分说明了《煤炭学报》刊出的论文水平之高、影响力之大。在此,编辑部向2篇论文的作者表示祝贺和感谢。
Numerical simulation of coal uniaxial loading acoustic emission based on SPH
SUN Chao-qun1,2,3,CHENG Guo-qiang2,LI Shu-cai1,LI Li-ping1,3,XU Zhen-hao1,GUO Ming1,LIN Peng1
(1.Research Center of Geotechnical and Structural Engineering,Shandong University,Jinan 250061,China;2.Mine Disaster Prevention and Control Laboratory,Shandong University of Science and Technology,Qingdao 266590,China;3.Key Laboratory of Coal Resources Exploration and Comprehensive Utilization,Ministry of Land and Resources,Xi’an 710054,China)
The SPH(Smoothed Particle Hydrodynamics)method was applied to study the acoustic emission effect in uniaxial compression test of coal with different homogeneous degree m.The change law of acoustic emission effect with the homogeneous degree was obtained.With the increasing of the homogeneous degree,the AE effect modes changes gradually from the swarm shocks to the pre-main-after shocks,and then to the main shocks.The ability of accumulation energy gradually increases with the homogeneous degree.The material properties of specimens changes from the ideal elastic-plastic material to the extreme brittle material.The mode of coal specimens’failure changes from the plastic flow failure to the brittle failure.The impact failure of specimens increases with the homogeneous degree.
SPH;acoustic emission;homogeneous degree;uniaxial loading
TD315
A
0253-9993(2014)11-2183-07
2013-11-11 责任编辑:常 琛
国家重点基础研究发展计划(973)资助项目(2013CB036000);国土资源部煤炭资源勘查与综合利用重点实验室开放课题资助项目(KF2013-5);山东大学基本科研业务费专项资金资助项目(2014GN028)
孙超群(1986—),男,山东泰安人,博士研究生。E-mail:scq86320@163.com。通讯作者:许振浩(1985—),男,湖北利川人,讲师,博士。E-mail:zhenhao_xu@sdu.edu.cn
孙超群,程国强,李术才,等.基于SPH的煤岩单轴加载声发射数值模拟[J].煤炭学报,2014,39(11):2183-2189.
10.13225/ j.cnki.jccs.2013.1655
Sun Chaoqun,Cheng Guoqiang,Li Shucai,et al.Numerical simulation of coal uniaxial loading acoustic emission based on SPH[J].Journal of China Coal Society,2014,39(11):2183-2189.doi:10.13225/j.cnki.jccs.2013.1655

