基于2DGabor小波与BDPCA的掌纹识别

薛延学,薛 萌,刘一杰,白晓辉

(西安理工大学信息科学系,西安710048)

基于2DGabor小波与BDPCA的掌纹识别

薛延学,薛 萌,刘一杰,白晓辉

(西安理工大学信息科学系,西安710048)

提出一种解决双向主成分分析(BDPCA)中小样本问题的掌纹识别方法。把掌纹感兴趣区域图像经过2DGabor小波变换后得到的每个图像都作为独立的样本,以增加每一类掌纹的样本数。设计一种基于样本散度矩阵的改进BDPCA算法进行特征提取。采用训练样本的k值矩阵代替训练样本的平均值矩阵,从而获得最优投影矩阵。将2DGabor与改进的BDPCA算法相结合进行掌纹识别。在PolyU掌纹库中的实验结果表明,该方法不仅减少了不同训练样本对识别率的影响,而且能够提高识别率,甚至当每类训练样本数仅为1时,也能得到较高的识别率,有效解决了掌纹识别的小样本问题。

掌纹识别;小样本问题;2DGabor小波变换;双向主成分分析;特征提取;散度矩阵

1 概述

掌纹识别是生物特征识别技术中一个新的研究领域,它旨在根据人体掌纹之间的差异进行身份识别,与其他生物识别技术相比,掌纹拥有主特征明显、稳定、易于采集和用户接受程度高等诸多优点[1],是一种有着广泛应用前景的生物识别方法。从上世纪末提出以来,掌纹识别技术得到了长足的发展,涌现了大量的识别算法[2-3]。

基于子空间的主成分分析(Principal Component Analysis,PCA),是一种成功的线性鉴别分析方法。PCA方法是将图像转化成一维向量的分析。由于图像转化为一维向量的维数一般较高,会增加特征提取的计算复杂度,并且如果训练样本太少的话,很难计算该向量的散度矩阵,会产生小样本问题[4]。为此,文献[5]提出了二维主成分分析(Two Dimensional Principal Component Analysis,2DPCA)的方法。基于图像矩阵的主成分分析,将图像矩阵变换为若干行向量或列向量的组合,构建二维图像矩阵的散度矩阵,得到的散度矩阵较小,所以在提取特征值时计算量较小、速度较快,同时能在一定程度上解决小样本问题。作为2DPCA方法的推广,由文献[6]提出的双向主成分分析(Bidirectional PCA,BDPCA)方法,已应用于人脸和掌纹识别。该方法通过分别计算行投影矩阵和列投影矩阵,将掌纹图像最终变换成一个矩阵,尽可能地对特征维数进行压缩,使得保存特征所需要的存储空间更小,匹配速度更快。

然而,传统BDPCA方法通常对每个类别的掌纹都需要多个训练样本,当每类的训练样本小于3个时,该方法的识别率下降很大,而且训练样本的选取对识别结果影响较大[2]。为了解决该问题,本文提出一种2DGabor小波变换和改进BDPCA结合的掌纹识别新方法,首先把定位分割后的ROI掌纹样本利用2DGabor进行小波变换,得到多个纹理特征输出子图像,然后将每个输出图像都作为独立样本,这样就综合了多个局部特征,增加了每一类掌纹的训练样本,由此解决了小样本问题,减少了训练样本的选取对识别结果的影响。此外针对传统的BDPCA方法中采用的训练样本的平均值不一定是训练样本分布的中心[7],设计了一种采用最小值矩阵进行散度矩阵计算的改进算法,能够获取ROI图像的最佳特征值。

2 算法介绍

2.1 2DGabor小波变换

2DGabor小波变换在分析图像局部频率和方向信息上具有优势,能够很好地兼顾信号在时域和频域中的分辨能力,可以充分描述图像的纹理信息,该方法与基于子空间的方法相结合已成功应用于人脸和掌纹识别[8-9]。

2DGabor小波滤波器的函数形式为[10]:

其中,μ,ν分别决定Gabor小波核的方向和尺度;Z= (x,y)为坐标值。

掌纹图像的纹理特征子图是让128×128的掌纹ROI图像与2DGabor滤波器核函数做卷积运算得到:

经过2DGabor小波分析,发现获得的特征向量是没有分析前图像的15倍,这么大维数的特征向量不仅不适合用来进行分类识别,而且造成了后续进行二次特征提取的计算困难。所以当对图像进行2DGabor小波变换后首要的任务是对图像进行下采样来降低它的特征维数,本文采用文献[7]使用的对掌纹图像进行小波分解的方法,使得下采样后将128×128的掌纹图像降为32×32。通过2DGabor变换及下采样后的效果样例如图1所示。

图1 掌纹ROI图像经过2DGabor变换及下采样后的效果

2.2 BDPCA算法

设训练样本图像有M个m×n维的图像样本I1,I2,…,IM,第j个训练样本图像的图像样本矩阵Ij可以用n个m×1的列向量进行表示,组成训练样本集。按照2DPCA[4]的方法,可计算出去行相关性的列方向上总的散度矩阵为:

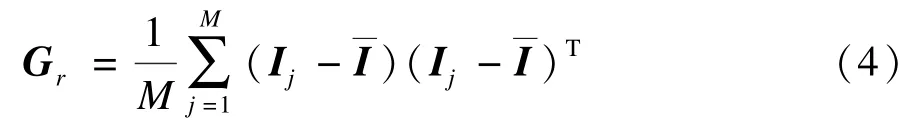
同样,可以将第j个训练样本图像的图像样本矩阵Ij用m个1×n的行向量进行表示,组成训练样本集,可计算出去列相关性的行方向上总的散度矩阵为:

与2DPCA算法相似,BDPCA算法是将矩阵Gr的特征值按从大到小进行排列,把前d1(d1≤M)个特征值的特征向量ui(i=1,2,…,d1)计算出来组成m×d1的矩阵,就是列映射矩阵U,其中,ui表示与Gr的第i个最大特征值有相关性的特征向量。同样,选取Gc的前d2d2(d2≤M)个与最大特征值有相应的特征向量vi(i=1,2,…,d2)组成n×d2的矩阵,就是行映射矩阵V。因此,图像矩阵I的特征矩阵为:

其中,Fj大小为d1×d2维特征矩阵,因为一般情况下取d1和d2都远小于M,所以该方法比2DPCA计算复杂度更低,效率更高。

2.3 改进的BDPCA算法

BDPCA掌纹识别属于典型的小样本问题,在训练样本数目小于3的情况下,传统的BDPCA算法是在不能够确定均值就是样本分布中心的情况下用它来建立散度矩阵的方法。针对该问题,在去行相关性和去列相关性的2个总体散度矩阵公式中不用训练样本图像总体的均值矩阵I—,而是选择一个适当的值用来替换均值,以便克服均值和类中心不一致时,对求取最优投影矩阵的影响。具体做如下改进:

设将M幅m×n维的图像序列Ij(j=1,2,…,M)作为训练样本,改进后的BDPCA算法分别定义去行相关性和去列相关性的总体散度矩阵为:

其中,Gr是列方向的总体散度矩阵;Gc是行方向的总体散度矩阵;N矩阵命名为k值矩阵(k=1,2,…,M)。

k值矩阵算法步骤为:将M个样本在矩阵中同一坐标位置的像素值,按照从小到大的顺序进行排列,让每个位置均选择重新排列的像素值序列中的第k个大小的像素值,这样就得到了k值矩阵。其中,k=1是选择M个样本中同一个坐标上像素值最小的那个像素值组成的矩阵,k=M是选择M个样本中同一个坐标上像素值最大的那个像素值组成的矩阵。

除上述改变外,求取图像矩阵I的特征矩阵方法与BDPCA相同,即图像矩阵I的特征矩阵为:

其中,Fj大小为d1×d2维特征矩阵,一般情况下取d1和d2都远小于M。

经过测试,发现改进后的BDPCA算法随着k值的不同会带来不同的识别效果。

3 实验结果与分析

本文实验采用香港理工大学PolyU掌纹库,所有实验均在CPU为Intel(R)Core(TM)i5-2430M (主频2.40 GHz)、内存2 GB下,应用Matlab7.0软件编写程序及测试。

具体算法步骤为:首先对掌纹图像进行预处理。其中包括原图像(384×284)二值化、连通域分析去噪、轮廓提取和定位分割5个过程,获得了感兴趣区域ROI图像(128×128)。其次对每个掌纹样本利用2DGabor小波进行滤波处理,得到15个输出图像,并将每个输出图像都作为独立的样本,以增加每一类掌纹的训练样本数,然后利用二层小波变换进行一个下采样,将掌纹ROI图像由128×128变为32×32,有效减少了数据量。第3步分别使用PCA、2DPCA、BDPCA、改进BDPCA及加入2DGabor小波的方法对ROI图像进行特征提取。最后为不失一般性,匹配采用最近邻分类器和欧式距离度量的方法对掌纹图像进行分类识别。

3.1 改进的BDPCA算法验证实验

实验从PolyU掌纹库的100人,每人左右手各3幅共600幅图像中,任意选取每人的3幅图像组成训练集,其余的3幅图像组成识别集,这样训练集和识别集各有300个样本。实验重复选取3次组合,并取3次的平均值作为最终识别结果。

实验采用2.3节所述的改进BDPCA算法,针对PolyU掌纹库,不同维数下k值与正确识别率对应关系的测试结果如图2所示。其中,k=1,2,…,300,这是因为训练集大小为300,而特征维数就是前文所提到的d1和d2。当选择不同的k值矩阵时,就会得到不同的正确识别率。

图2 不同维数下k值与正确识别率的关系

由图2不难发现,如果进行横向比较,即在特征维数不变的情况下,正确识别率呈现一个先降后升的趋势;而进行纵向比较,即k值不变,而改变特征维数,正确识别率呈现了一个上升的趋势。当k=1和k=300(即k取像素值最大值和最小值)均能保证获得最优投影矩阵。

此外,以特征维数8×8的情况为例,使用均值矩阵和k=1的矩阵这2种不同的矩阵作为作差矩阵N,分别测试得到的正确识别率如表1所示。

表1 不同散度矩阵的识别结果 %

上述实验表明,该算法采用训练样本的k值矩阵代替训练样本的平均值矩阵,改进了总体散度矩阵的定义,提高了BDPCA算法的识别率。因此,本文采用k=1时像素值最小的矩阵作为改进BDPCA的N矩阵,以获得最优投影矩阵。

3.2 不同特征提取方法的对比实验

实验从PolyU掌纹库的600幅图像中,选取训练集、识别集、重复测试以及求取平均值的方法与3.1节相同。实验对PCA、2DPCA、BDPCA以及改进BDPCA这4种特征提取方法分别加入2DGabor的识别性能进行测试。测试结果如表2所示。

表2 不同特征提取方法的识别结果

从表2测试结果可以看出,改进BDPCA的方法相对于PCA、2DPCA和BDPCA具有更好的识别率,识别时间更快。而通过2DGabor扩充样本数使得上述方法的识别率均有所提高,证明了通过2DGabor小波变换增加样本数可以提高上述特征提取方法的正确识别率。

3.3 小样本实验

首先针对单一样本进行BDPCA、改进BDPCA和加入2DGabor后的特征提取方法测试。实验中,从PolyU掌纹库的100个人对应的600幅图像中,随机对每个人的6幅掌纹图像进行1～6编号,将每个手掌编号相同的图像组成有100个样本的训练集,其余的图像组成有500个样本的识别集。这样就有6种样本情况,分别进行实验,重复选取3次的平均值作为最终识别结果,测试结果如表3所示。

表3 单一样本下3种特征提取方法对应的正确识别率 %

从表 3中可以看出,改进 BDPCA方法比BDPCA方法在识别率上有小幅提升,但均存在训练样本选取不同时对正确识别率影响较大的问题。而通过加入2DGabor可以减少不同训练样本对识别率的影响,并能使识别率大幅提升。

此外,为了更好地验证2DGabor小波变换对基于DBPCA及改进BDPCA的小样本问题的解决效果,从PolyU掌纹库的600幅图像中,任意选取每人的1幅、2幅和3幅掌纹图像组成100幅、200幅和300幅不同的训练集,对应剩余的500幅、400幅和300幅图像组成识别集。实验重复选取3次组合,并取3次的平均值作为最终识别结果。具体测试结果如表4所示。

表4 不同训练样本下对应的平均正确识别率 %

从表4可以看出,随着训练集样本个数的减少, BDPCA和改进BDPCA的正确识别率下降很快,而加入2DGabor后使得小样本情况下2种方法的识别率下降缓慢。在样本集中每人仅有一幅训练样本时,改进BDPCA还可以达到95.07%的识别率。

4 结束语

本文主要研究了基于子空间的掌纹识别如何有效地解决小样本的问题。与已有算法不同,本文将掌纹样本通过2DGabor变换后的每一个图像都作为一个新的训练样本,这样就扩大了总的样本数,并与改进的BDPCA算法相结合,提出了2DGabor+改进BDPCA的掌纹识别方法,解决了掌纹识别中的小样本问题。在PolyU掌纹库(版本1)中的实验结果表明,该方法不但可以减少不同训练样本对识别率的影响,并能使正确识别率大幅提升,甚至当每类训练样本数仅为1时,本文方法仍然能达到95.07%的识别率,证明了该方法的有效性。

[1] 苑玮琦,柯 丽,白 云.生物特征识别技术[M].北京:科学出版社,2009.

[2] 岳 峰,左旺孟,张大鹏.掌纹识别算法综述[J].自动化学报,2010,36(3):354-365.

[3] 林 森,苑玮琦.掌纹感兴趣区域定位与选择方法综述[J].计算机工程与应用,2011,47(14):21-24.

[4] Raudys J S,Jain K A.Small Sample Size Effects in Statistical Pattern Recognition:Recommendations for Practitioners[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1991,13(3):252-264.

[5] Yang Jian,Zhang D,Frangi A F,et al.Two-dimensional PCA:A New ApproachtoAppearance-basedFace Representation and Recognition[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2004,26 (1):131-137.

[6] Zuo Wangmeng,Zhang D,Wang Kuanquan.An Assembled Matrix Distance Metric for 2DPCA-based Image Recognition[J].Pattern Recognition Letters, 2006,27(3):210-216.

[7] Li Xiaodong,Fei Shumin,Zhang Tao.Median MSD-based Method forFace Recognition[J].Neurocomputing,2009,72(16/18):3930-3934.

[8] 聂祥飞,谭泽富,郭 军.基于Gabor变换和双方向PCA的人脸识别[J].计算机工程与应用,2007,43 (36):13-15.

[9] 苏 斌,姜 威.一种基于Gabor变换和2DPCA的掌纹识别改进算法[J].计算机应用与软件,2011,28 (1):242-245.

[10] 屈会芳.基于特征融合的掌纹识别算法应用研究[J].计算机仿真,2012,29(6):265-268.

[11] Lu Jiwen,Zhang Erhu,Kang Xiaobin,et al.Palmprint Recognition UsingWaveletDecompositionand 2D Principal Component Analysis[C]//Proc.of International Conference on Communications,Circuits and Systems.[S.l.]:IEEE Press,2006:2133-2136.

编辑 顾逸斐

Palmprint Recognition Based on 2DGabor Wavelet and BDPCA

XUE Yan-xue,XUE Meng,LIU Yi-jie,BAI Xiao-hui
(Department of Information Science,Xi'an University of Technology,Xi'an 710048,China)

A palmprint recognition method which can solve the small sample size problem of bidirectional Principal Component Analysis(PCA)is presented.The implementation procedure of this method is as follows:Each image is obtained by 2DGabor wavelet transform of palmprint Region of Interest(ROI)image as an independent sample,in order to increase the number of the samples of every kind palmprint.This paper designs an improved algorithm based on samples scatter matrix to extract the palmprint features.This algorithm can obtain the best projection matrix by adopting the k values matrix instead of the average values matrix of training samples.The 2DGabor and the improved BDPCA algorithm are combined to identify every palmprint.Experimental results on the PolyU palmprint database demonstrate that the proposed method not only reduces the influence of different training samples on recognition rate,but also increases the rate,especially it has great performance when the number of training samples is 1.The method effectively solves the small sample size problem of palmprint recognition.

palmprint recognition;small sample size problem;2DGabor wavelet transform;Bidirectional Principal Component Analysis(BDPCA);feature extraction;scatter matrix

1000-3428(2014)09-0196-04

A

TP391.4

10.3969/j.issn.1000-3428.2014.09.039

陕西省教育厅自然科学研究计划基金资助项目(2010JK741)。

薛延学(1963-),男,副教授,主研方向:模式识别;薛 萌、刘一杰,硕士研究生;白晓辉,硕士。

2013-10-28

2013-12-23E-mail:xue_yx@163.com