基于最早截止期优先算法的过渡过程研究
钱光明
(湖南师范大学数学与计算机科学学院,长沙410081)
基于最早截止期优先算法的过渡过程研究
钱光明
(湖南师范大学数学与计算机科学学院,长沙410081)
在以最早截止期优先算法调度的实时系统中,如果出现新任务插入和/或现行任务加速要求,而系统所剩带宽又不足时,必须进行带宽转让,系统运行模式将被迫发生改变。针对该问题,研究新任务插入和/或现行任务加速的动态过程,分析带宽转让对系统可调度性的影响。应用处理器需求准则,证明截止期丢失只可能出现在某一时间点之前。通过该结论可以合理定义过渡过程的长度,从而展示一个清晰的三阶段模型。最后给出相关仿真实例。
带宽转让;任务插入;模式改变;过渡过程;截止期;处理器需求准则;最早截止期优先算法
1 概述
模式改变存在于诸多实际应用中。例如,当一台电脑开机而长时间无人操作时,自动进入屏幕保护就是一种模式改变;一部手机正在用于电子游戏过程中,突然有电话到来,游戏暂停而进入通话模式,也是一种模式改变。
目前,众多的嵌入式芯片更是专门设计了多种模式供设计者选择,如运行模式、空闲模式、省电模式等。多模式的引入,往往是为了系统的有限资源得到尽可能合理而充分的利用。
一般地,当系统的某些内部状态发生有效改变,或是探测到某些外部事件时,便会引起模式改变[1]。
为满意地完成一个模式改变,有许多问题需要研究[1-2]。例如,采用何种策略进行。可调度性如何[3]。过渡过程的长度如何定义和计算,过渡过程对系统有何影响等[4-5]。显然,对这些问题的回答,与具体系统结构、具体调度算法以及应用场合等诸多因素有关。
本文研究的是这样一种模式改变:一个以最早截止期优先(Earliest Deadline First,EDF)算法调度的周期性实时系统中,当有新任务要求插入和/或现行任务要求加速,而系统所剩带宽又不足时,必须要进行带宽转让,系统运行模式将被迫发生改变。此处的系统所剩带宽,指的是1(即100%)减去所有现行任务的使用率(带宽)之和。
这样的任务插入和加速问题,可联想到某些实际应用场合。如机器人目标逼近测量时,目标越近,负责测量的任务周期应该越短,使用率增加(加速)。又如一个网络通道中,如果带宽基本被现有用户用完,而新用户又要进来时,只好压缩旧用户的带宽以容纳新用户的插入。
EDF是一个经典调度算法[6-7]。文献[6]证明了只要所有任务使用率之和不大于1,系统就是可调度的,即不会出现截止期丢失的情况。但当插入和加速引起模式改变时,这一可调度性准则是否合适仍然是个问题。因此,本文将通过分析和证明指出,只要新模式时所有任务使用率之和不大于1,截止期丢失就只可能出现在某一时间点之前,而系统在新模式下一定是可调度的。同时合理地将过渡过程的长度定义为tr到该时间点之间。
2 相关研究
当系统从一种模式过渡到另一种模式时,可以用图1来简单表示。其中,tr表示模式改变的要求时刻。在该时刻之前系统运行于旧模式,或称现行模式。tr之后系统进入过渡过程,然后工作于新模式。

图1 模式改变对应的3个阶段
实时系统虽然有数十年的研究历史,但任务插入和加速这一模式改变问题,一直有相当的研究难度。如文献[4]发现一个有趣现象:动态加入一个新任务时,如果不很小心,会出现截止期丢失的情况。但当时并未深入研究。
关于EDF算法的任务插入和/或加速问题,文献[8]给出了一个弹性调度模型。当系统剩余带宽不足时,对现行任务进行压缩,以应对插入和/或加速。该模型中求出了一个时间点,指出只要不早于该点,插入和/或加速就不会引起截止期丢失。文献[9]证明了这样的时间点还可以更早些,并且加速问题可以等效为插入问题来研究(故下面只以插入来描述模型即可)。因此,什么是最早的、不引起截止期丢失的时间点(文献[8]称为最早可行时刻),并非本文的研究内容。文献[8-10]均未指出截止期丢失可能出现的区间,均未明确过渡过程到底该算到何时为止,这正是本文要研究解决的问题。
首先通过以下定义列出关于任务压缩的模型[9]。
定义 任务压缩




图2 任务压缩示意图

3 过渡过程
由上可知,tr前夕,现行任务集为(τi,Γ)。要研究过渡过程以及系统的可调度性,一般选择从现行任务集的运行起点tLCM0开始[9]。且注意有式(1)表达的时间次序。

此外,相关定理的证明中要用到处理器需求准则[11-12]:当且仅当任务集中所有任务的处理器需求之和小于等于1时,任务集是基于EDF可调度的。
一个任务在一个时间段内的处理器需求,等于该时间段内该任务必须要完成的执行量。
从tLCM0到任意时间点t,新任务的处理器需求之和表示为:

其中,J代表新任务组成的子集;Unew为该子集中各任务使用率之和;Uj为其中某一任务的使用率;rj为其释放时刻;rJ为它们中最早发布的那个任务的释放时刻,rJ≥tr。最坏情况是所有新任务同时在rJ=tr时刻释放。
未受压的现行任务处理器需求之和为:
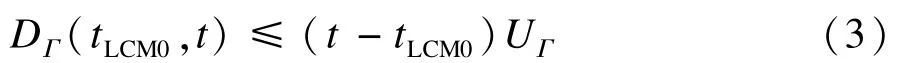
综上,如果受压任务τi的处理器需求为Di(tLCM0,t),则系统所有任务处理器需求之和为:

再引入符号Δ:

那么,依据上述处理器需求准则[11-12],当且仅当Δ≥0时,系统是可调度。下面的证明将用到这一结论。
定理1 基于EDF可调度的周期性实时任务集中,tLCM0为任务集运行的起点时刻。从tr开始压缩任务τi(Ci,Ti)以出让带宽给新任务。在[tLCM0,t0+Ti)期间,一定不会出现任何任务超截止期的情况。
证明:∀t∈[tr,t0+Ti),τi在[tLCM0,t]间的处理器需求:

那么,依据式(2)和式(3),有:

因此:

所以,系统在该时间段可调度,即不会出现截止期丢失情况。证毕。
由定理1可知,在时间点t0+Ti之前,系统总是可调度的。


基于式(2)和式(3),有:

因此:

显然,Δ≥0表明该时间段内系统总是可调度的。证毕。
由定理2可知,当时间大于或等于t0+Ti′时,系统总是可调度的。
证明:由定理1和定理2可直接得出此推论。

4 仿真示例
虽然经过了上述证明,仍然有必要进行示例验证。在EDF实验平台上的大量仿真表明上述定理是准确无疑的。图3为示例之一。

图3 任务压缩和插入的模式改变示例

t0+Ti=8,t0+=16。依据上述定理和推论,该例中的过渡过程应是[4,16)这一时间段,截止期丢失只可能出现在这一期间。如图3所示,τj(1,4)的第一个作业截止期未能得以满足,本该完成的一个单位长执行量被延误到第2个周期的t=8和t=9之间才完成。
新模式从t0+=16开始,从该点及以后的时间内,所有作业截止期都能满足。本例中有意选择τi, τk和τj,使它们在该点均开始一个新的作业,以便可以明显看出后面是可调度的。实际上,即使不如此,上面的定理也保证了新模式下一定不会再出现截止期丢失。
5 结束语
关于任务压缩和插入的模式改变,尽管旧模式和新模式下均满足所有任务使用率之和不大于1,但仍然有可能出现截止期丢失。本文证明了这种丢失只可能出现在过渡过程[tr,t0+)中,这将成为今后继续研究的一个重要基础。但本文讨论的是压缩单个任务τi,因此,同时压缩多个任务时能得到何种结论是需要进一步研究的课题。此外,即使是单任务压缩,如何确定最早的时间点,使新任务的插入不至于引起截止期丢失,也仍然需要深入研究。
[1] Real J,Crespo A.Mode Change Protocols for Real-Time Systems:A Survey and a New Proposal[J].Real-Time Systems,2004,26(2):161-197.
[2] Sha L,Rajkumar R,Lehoczky J,et al.Mode Change Protocols for Priority-Driven Preemptive Scheduling[J]. Real-Time Systems,1989,1(3):243-264.
[3] Pedro P,BurnsA.Scheduabilty AnalysisforMode Change[C]//Proc.of the 10th EUROMICRO Workshop on Real-Time Systems Symposium.Berlin,Germany: [s.n.],1998:172-179.
[4] PillaiP,Shin K G.Real-Time Dynamic Voltage Scaling for Low-Power[C]//Proc.of the 18th ACM Symposium on Operating Systems Principles.Banff,Canada:[s.n.], 2001:89-102.
[5] Qian Guangming,ChenXianghua,YaoGang.Two Methods to Release a New Real-time Task[J].Indian Journal of Computer Science and Engineering,2012,3 (1):75-81.
[6] Liu C L,Laylan J W.Scheduling Algorithms for Multiprogramming in a Hard Real-Time Environment[J]. Journal of the ACM,1973,20(1):40-61.
[7] Baruah S.Partitioned EDF Scheduling:A Closer Look [J].Real-Time Systems,2013,49(6):715-729.
[8] Buttazzo G C,LipariG,CaccamoM,etal.Elastic Scheduling for Flexible Workload Management[J].IEEE Transactions on Computers,2002,51(3):289-302.
[9] Qian Guangming.An Earlier Time for Inserting and/or Accelerating Tasks[J].Real-Time Systems,2009,41(3): 181-194.
[10] 钱光明,姜 辉,陈湘华.实时任务调度算法最早可行时刻的求取模式[J].计算机工程,2012,38(4): 284-286.
[11] Barauh S K,Howell R R,Rosier L E.Algorithms and Complexity Concerning the Preemptive Scheduling of Periodic Real-Time Tasks on One Processor[J].Real-Time Systems,1990,2(4):301-324.
[12] Jeffay K,Stone D L.Accounting for Interrupt Handling Costs in Dynamic Priority Task Systems[C]//Proc.of the 14th IEEE Real-Time Systems Symposium.Raleigh-Durham,USA:[s.n.],1993:212-221.
编辑 金胡考
Research on Transition Process Based on Earliest Deadline First Algorithm
QIAN Guang-ming
(College of Mathematics and Computer Science,Hunan Normal University,Changsha 410081,China)
In a real-time system scheduled with the Earliest Deadline First(EDF)algorithm,if the request of new tasks'insertion and/or current tasks'acceleration occurs and the remaining bandwidth of the system is not enough for this request,then part of the bandwidth has to be freed and the system will change its running mode.Aiming at this problem,this paper discusses the influences on the schedulability by the mode change based on the analysis on the dynamic processes of the insertion of a new task and/or the acceleration of a current task.With the processor demand criterion,it proves that deadline missing is possible only before a time point.Hence the length of the transition can be reasonably defined,and it results a clean research model of three stages.Illustrative examples are also given.
bandwidth transfer;tasks insertion;mode change;transition process;deadline;processor demand criterion; Earliest Deadline First(EDF)algorithm
1000-3428(2014)09-0055-04
A
TP316.2
10.3969/j.issn.1000-3428.2014.09.012
长沙市科技局基金资助项目(K11ZD014-13)。
钱光明(1963-),男,教授,主研方向:实时系统,嵌入式应用。
2013-09-03
2013-10-27E-mail:qqyy@hunnu.edu.cn

