基于偏最小二乘的无线传感网多跳定位算法

窦如林,阎 浩,严筱永

(1.金陵科技学院软件工程学院,江苏 南京 211169;2.金陵科技学院智能科学与控制工程学院,江苏 南京 211169)

基于偏最小二乘的无线传感网多跳定位算法

窦如林1,阎 浩1,严筱永2

(1.金陵科技学院软件工程学院,江苏 南京 211169;2.金陵科技学院智能科学与控制工程学院,江苏 南京 211169)

提出了一种基于偏最小二乘的多跳定位算法(ML-PLS)。算法借助偏最小二乘对已知节点间的跳数与真实距离的建模,通过跳数、距离两者间的最大协方差共同推动节点位置的估计。ML-PLS算法对复杂部署环境具有较强的适应性,克服了传统算法只适用于各向同性网络的不足。仿真结果表明,ML-PLS算法定位精确度高且性能较稳定,并能适应不同网络环境。

多跳定位;无线传感器网络;偏最小二乘

无线传感器网络[1-2](Wireless Sensor Network,WSN)是一种综合了传感器技术、嵌入式计算机技术、现代网络及无线通信技术、分布式信息处理等技术的新一代网络技术。与以往的网络不同,无线传感器网络是一种以数据为中心的网络,因而数学统计、多元分析方法是传感网中常见的问题解决手段。随着无线传感器网络技术快速的发展,传感器网络的应用越来越多,在各种应用中,检测到事件后一个重要问题就是该事件发生的位置。文献[3]中统计,约80%的上下文感知信息与节点位置有关,在许多传感器网络应用中节点的位置信息起着关键性的作用。

目前,根据定位过程中是否用到距离测量技术可以粗略地将定位分为:基于测距定位方法和基于非测距定位方法[4-5]。基于测距的定位方法通过测量节点间的距离或方位获取未知节点的位置,该方法定位精度高,但容易受温度、障碍物等环境因素的影响,且测量半径受到所带电量限制,因此,不适合大规模定位。基于非测距定位方法大都是基于节点之间的连接关系(多跳关系),在假设跳数与单跳距离之间存在某种函数映射关系之上来估计节点的位置。该方法思想简单,易于实现,对硬件要求相对较低,非常适合大规模场景下的定位应用。然而,与众多关键技术一样,在实际应用中非测距多跳定位技术性能仍然受到诸多技术难题困扰,其中最致命的是多跳定位仅能在节点密度高且分布均匀的各向同性网络取得较理想的定位结果,而在节点分布不均、稀疏等网络环境各向异性的情况下,定位效果极差。

针对多跳定位所存在的问题,提出一种更符合实际环境下使用且计算复杂度相对较低、定位精度较高、适应能力更强的多跳定位方法,即ML-PLS(Multihop Localization-Partial Least Squares)。ML-PLS方法尝试利用传感网本身的拓扑结构与自身特性来进一步提高定位算法的性能,使其适应不同的环境。

1 相关研究

近年来,借助多元分析对定位机制进行建模和算法设计已成为研究热点之一[6-7]。该方法利用已知节点分布特性与测量信息之间的对应关系,关联并构建一个映射模型,而后应用该模型估计出未知节点的位置。多元分析与以往方法相比较,能有效地挖掘出数据背后所隐含的网络拓扑结构、相关性等信息。Lim等人提出了一种采用TSVD(Truncated Singular Value Decomposition)技术对跳数与真实距离建模的PDM(Proximity Distance Map)定位算法[8]。PDM方法首先将采集到的已知节点间路径的物理距离和测量距离分别用矩阵进行标示,而后通过TSVD方法对两个矩阵进行线性转换获得一个最优线性转换模型,再将未知节点到信标节点的最短跳数带入模型,进而估计出未知节点到信标节点的物理距离。TSVD[9]实质上是一种线性多元规则方法,利用其获得估计距离实质上是未知节点所关联的已知节点估计值的加权和,因此获得估计值与真实值较为接近;此外TSVD方法舍弃了较小奇异值,在一定程度上减少噪声在转换过程的影响,从而达到避免定位中的共线性问题,增加算法的稳定性。PDM方法能够在一定程度上解决节点分布不均、网络拓扑各向异性等原因造成的定位精度不高问题。但PDM方法仍然存在3方面的不足:1)TSVD是通过设置一个阈值k直接将奇异值中小于阈值k的设置为0,如果k值选择合理,TSVD的解稳定,反之则会使算法性能下降;2)PDM方法未对跳数与真实距离进行标准化处理,不同的量纲造成一定程度数据淹没现象;3)TSVD建模只考虑跳数信息而未顾及真实距离信息,使获得的模型并不能真正反应跳数与真实距离的关系。Lee等人[10]受到PDM方法启发,提出了基于SVR的定位方法——LSVR,该定位方法能够适应不同网络环境,且在小样本情况下仍然能获得较好的定位精度。但基于支持向量机(Support Vector Machines,SVM)回归方法是一种多输入单输出算法[11],在实际定位中需多次建模,使得算法复杂度急剧上升,且随着信标节点数量的增大,定位计算所需的时间和空间资源都会成几何级数增长。为了降低定位问题的复杂性,提高定位方法的泛化性能,简化定位模型,非常有必要在构建模型前对数据进行特征提取。研究人员发现,偏最小二乘(Partial Least Squares,PLS)[12-13]方法能很好地实现输入到输出的特征提取。

PLS是一种将输入变量与输出变量投影到相应的低维特征空间,在分别得到正交特征向量后,利用最大协方差共同决定预测方向。PLS预测性能强,适合处理小样本数据、自变量之间的多重共线,抗噪能力强预测精度高且具有较好的泛化能力,PLS方法无需事先获知样本的分布模型,它又被称为第2代回归方法。本文借鉴PLS和普通的多跳定位算法(Ordinary Multihop Localization,OML)原理,将两者相结合,提出一种新非测距定位方法,即ML-PLS。方法通过收集和利用实际距离和节点间跳数信息,关联并构建其间的最优关系(模型),并用此模型预测未知节点到已知节点距离。

2 偏最小二乘法简介

偏最小二乘法是一种基于数学优化的多元统计数据分析方法,由S.Wold和C.Albano[13]在1983年首先提出。PLS将多元线性回归、主成分分析和典型相关分析有机地结合起来。PLS在进行回归之前,利用协方差指导输入变量和输出变量的特征选取,由于在选取过程中采用了信息综合和筛选技术,因此PLS方法不仅有效克服输入变量的相关性,从而消除了共线性问题对回归的影响,而且在回归时强调输入对输出的解释和预测作用,因而去除了对回归无益的噪声,使得PLS方法具有更好的鲁棒性和预测稳定性。由于PLS方法总是将多元回归问题转化为若干个一元回归问题,因此它还具有适应小样本的特性,正是由于有如此多的优良特性,使其非常适合传感网的定位。

线性PLS方法是综合考虑输入变量P和输出变量L,通过迭代的方法对成分t、u(t是变量P的线性组合,u是变量的L线性组合)进行求解,原理见图1。

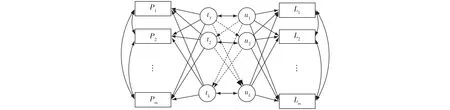
图1 偏最小二乘原理Fig.1 Partial least squares

从图1可以看到,P与L之间的交叉协方差是很重要的一个信息,希望通过k对潜在变量对来刻画这种交叉协方差,因此,PLS求解需要满足:1)t和u应尽可能地携带各自数据表中的变异信息;2)t和u的相关程度能够达到最大。PLS表述为优化问题的解

其中,w,c是权向量。

PLS算法的基本步骤如下:

1)首先对输入、输出变量进行标准化处理(包括减均值,初标准差等),以便消除输入输出变量的不同量纲对最终计算结果产生的影响;

2)分别从输入、输出变量P、L提取第1个主成分t1和u1,根据回归需要,需满足:

a)t1和u1,应尽可能地携带变量P、L中的变异信息,即,使得t1和u1的方差最大:Var(t1)→max, Var(u1)→max;

b)t1和u1间的相关程度能够达到最大,即,使得t1和u1的自相关达到最大:Corr(t1,u1)→max;

c)综合a)和b)得到优化目标,即,使得t1和u1的协方差达到最大

3)在第一个成分t1和u1提取后,分别实施P、L对t1上的回归。如果回归方程已经达到满意的精度,则PLS方法终止;否则,将利用P被t1解释后的残差以及L被u1解释后的残差进行第2轮的成分提取。如此往复,直到提取所有的自变量成分和因变量成分。

4)偏最小二乘的预测并不需要选择全部成分,一般仅需前k个成分,常用的成分选择方法有交差检验法和经验法等。

在实际应用中,数据受到很多不稳定因素的干扰,其中不仅包含数量较多、幅度较小的测距误差(随机噪声),还包含少量幅度较大的测距误差(奇异点或粗差),偏最小二乘方法仅仅能消除随机噪声的干扰,而对粗差却无能为力。为此,在偏最小二乘法中添加了异常值监测步奏,即:

5)在确定成分个数后,获得一成分表,随后计算每个样本点对k成分的累计贡献率。根据实际情况设定判断阈值Thre,并将贡献率高于Thre的样本点确定为异常。根据特雷西等人的研究[14],累计贡献率服从以下分布:

3 ML-PLS节点定位模型建立

基于PLS方法的节点定位分两个阶段:训练阶段和定位阶段。在训练阶段通过对已知节点间跳数和物理距离学习训练出测量到真实距离的映射,建立定位模型;在定位阶段,未知节点通过它到信标节点的跳数,运用训练得出的映射模型对未知节点进行位置估计。

从式(3)易知,P中的变量间也会存在严重的多重相关性或者P中的样本点数目少于变量个数情况,此时对等式(3)强行计算,估计结果将失效。此外,估计值η^的精度不仅仅与输入变量相关,还与输出变量L有关,输入与目标两者共同决定着η^的预测方向。

偏最小二乘是一种集多元回归、典型性相关分析和主成分分析于一体的多元数据分析方法,它利用输入与输出协方差指导特征的选择,能很好适应真实情况的建模和预测。将PLS运用到多跳定位方法中,能够适应不同的定位场景且能获得较高好定位精度。此时,利用PLS对跳数-真实距离建模过程可被归纳为以下算法(ML-PLS定位方法),其步骤如下:

输入:知节点跳数矩阵P=[p1,p2,…,pm];相应真实距离矩阵L=[l1,l2,…,lm],预测设定的主元

初始化u:u=li,其中,li是L中的任意一列向量;

计算P的权值向量w:w=PTu;

归一化t:t=Pw,t←t/‖t‖;

·属性定位策略。这种定位策略主要是依据服务活动本身的特点来进行定位。它更多地是因为活动设计本身具有一定的特色或者与其他类似服务的差异化而采取的策略。

计算L的权值向量c:c=LTt;

归一化u:u=Lc,u←u/‖u‖;

已收敛与其真值,则可以执行步骤7;否则转至步骤2,进行第k+1次迭代;

缩小矩阵P,L:P←P-t tTP,L←L-t tTL

根据式(2)判断数据中是否存在粗差,并加以处理;

4 ML-PLS的性能验证

非测距定位方法重要的特点之一是非常适合大规模部署,这就需要部署成百上千的传感器节点,而在目前的实验条件下很难实现如此大规模的真实网络。因此,在大规模非测距模节点定位算法的研究中,通常采用软件仿真的方式来评价定位算法的优劣。

本节通过仿真实验来分析和评价ML-PLS算法的性能。仿真在Matlab平台上进行,所有的编码都采用Matlab语言编写。实验考虑两种节点部署策略:规则部署和随机部署。对于信标节点,假设它们均匀地部署在被检测的区域内。为了降低一次实验结果的片面性,每种部署实验都进行了50次仿真,每次试验里节点都将重新随机分布在实验区域,取50次平均误差的开方(RMS)[15]的均值作为评价依据。

此外,本节的实验针对上文提出的基于PLS的定位算法、OML、基于TSVD的PDM定位算法和基于SVM回归的定位算法进行了比较。由于TSVD方法需要设定舍弃特征值门限;LSVR方法需要设定核参数、惩罚系数C和不敏感损失函数的宽度ε,为了公平起见,实验中TSVD方法设舍去特征值小于等于3相对应的特征向量;LSVR方法的C和ε设置参照文献[16],而核函数本文选择高斯核函数[12],其核函数与训练样本的距离有关,因此核参数设为训练样本均值的40倍。

4.1 规则部署

在这组实验中,分别有441个和333个节点规则地部署在600×600的正方形区域或C形区域内(方形区域内置一个300×260障碍物),实验在这些节点中选取30到40个节点作为信标节点。首先,考察两个ML-PLS方法的最终定位结果(图中信标节点数为36),如图2所示,圆圈表示未知节点,方块表示信标节点,直线连接未知节点的真实坐标和它的估计坐标,直线越长,定位误差越大。

图2 规则部署定位结果Fig.2 The positioning results of rule deploy

图3描述的是规则部署网络中信标节点数量对定位精度的影响。理论上在监测区域内信标节点越多,定位误差越小。由图3显示的结果可以看出,OML的RMS值最大且曲线上下起伏,其它3种方法的RMS值随着信标节点数目的增加而单调递减,且本文所提出ML-PLS方法定位精度最高。此外,还可以看出ML-PLS和LSVR方法在两种部署区域内的RMS曲线值相差不大,而其余方法相差较大,这也说明ML-PLS和LSVR方法具有较强的环境适应能力,能够适应网络拓扑的各向异性。由于PLS是多元回归方法,因此在计算过程中考虑了节点间的相关性,所以定位精度更高。从图3还可以看出ML-PLS随信标节点数量增加单调递减,但这种趋势非常弱,这也就说明了信标节点数量对其精度影响小,ML-PLS方法适应少信标节点环境,从图中可以看出在两种规则部署区域内,ML-PLS方法的平均定位性能分别相对于LSVR方法提高17.6%和10.5%。

4.2 随机部署

在这组实验中,500个节点随机地部署在600×600的二维正方形区域C内,并从这450个节点中规则地选取30到40个节点作为信标节点。图4显示的是含有36信标节点某次ML-PLS方法在两种形状下随机部署的定位结果。

图3 规则部署RMS曲线Fig.3 The RMS curve of rule deploy

图4 随机部署定位结果Fig.4 The positioning results of random deploy

图5描述的是随机部署网络中,信标节点的数目和RMS误差的关系。同规则部署一样,OML的RMS值最大且曲线上下起伏,且在C形区域定位误差大于方形区域,这都说明OML方法不稳定,对网络拓扑的各向异性明感。PDM方法虽然去除了部分小特征值相对应的数据,但由于舍弃都是人为设定,且未考虑跳数和真实距离量纲问题,虽定位精度较OML方法有所改进,但改进力度较小。LSVR方法与本文所提及的方法定位精度较为接近,但由于LSVR是一种多输入单输出方法,对于构建跳数与真实距离这样的矩阵关系,它显得有些力不从心,LSVR方法需要多次建模随经过优化但未考虑数据间的相关性,因此基于LSVR方法定位精度低于本文所提出的ML-PLS方法。从图5可以看出,ML-PLS方法相对于ML-PLS方法性能分别平均提高了3.3%和6.6%。

图5 随机部署RMS曲线Fig.5 The RMS curve of random deploy

5 结 语

本文提出了一种非测距定位方法——ML-PLS,该方法通过构建跳数与真实距离关系,建立测量距离与物理距离的模型,可以有效的处理无线传感器网络中拓扑结构复杂的问题,同时通过贡献率的判断算法能有效的鉴别出粗差数据。与同类算法相比,ML-PLS算法不仅继承了OML方法的优点,通过仿真实验表明在多种部署环境下,ML-PLS算法都能够取得较高的定位精度,并且受信标节点数目的影响较小。

[1]Emary I M M E,Ramakrishnan S.Wireless Sensor Networks:from Theory to Applications[M].United Kingdom:CRC Press,2013

[2]Khan S,Pathan A-S K,Alrajeh N A.Wireless Sensor Networks Current Status and Future Trends[M].United Kingdom: CRC Press,2013

[3]周艳.智能空间中定位参考点的优化选择及误差分析[D].沈阳:东北大学,2009

[4]Sand S,Dammann A,Mensing C.Positioning in Wireless Communications Systems[M].[s.l.]:wiley,2014

[5]Liu Y,Yang Z.Location,Localization,and Localizability Location-awareness Technology for Wireless Networks[M]. [s.l.]:Springer,2011

[6]陈祠,牟楠,张晨,等基于主成分分析的室内指纹定位模型[J].软件学报,2013,24(s1):98-107

[7]Afzal S,Beigy H.ALocalization Algorithm for Large Scale Mobile Wireless Sensor Networks:a Learning Approach[J]. The Journal of Supercomputing,2014,69(1):98-120

[8]Lim H,Hou J C.Distributed Localization for Anisotropic Sensor Networks[J].ACM Transactions on Sensor Networks (TOSN),2009,5(2):1-26

[9]Hogben L.Handbook of Linear Algebra[M].United Kingdom:CRC Press,2007

[10]Lee J,Chung W,Kim E.A New Kernelized Approach to Wireless Sensor Network Localization[J].Information Sciences,2013,243(2013):20-38

[11]Vazquez E,Walter E.Multi-output Support Vector Regression[C].13th IFAC Symposium on System Identification,2003: 1820-1825

[12]Shawe-Taylor J,Cristianini N.Kernel Methods for Pattern Analysis[M].London:Cambridge University Press,2004

[13]王桂增,叶昊.主元分析与偏最小二乘法[M].北京:清华大学出版社,2012

[14]肖磊.异常数据检测及其在神经模糊建模中的应用[D].厦门:厦门大学,2006

[15]Chen J,Wang C,Sun Y,et al.Semi-supervised Laplacian Regularized Least Squares Algorithm for Localization in Wireless Sensor Networks[J].Computer Networks,2011,55(10):2481-2491

[16]Cherkassky V,Ma Y.Practical Selection of SVM Parameters and Noise Estimation for SVM Regression[J].Neural Networks 2004,17:113-126

(责任编辑:马金玉)

Multihop Localization Algorithm Based on Partial Least Squares for Wireless Sensor Network

DOU Ru-lin,YAN Hao,YAN Xiao-yong
(Jingling Institute of Technology,Nanjing 211169,China)

An improved multihop localization algorithm(ML-PLS)based on partial least squares is proposed.This algorithm uses the partial least squares to build the localization model of hop-count and the real distances between beacons,and employs the maximun covariance of hop-count matrix and distance matrix to jointly promote the estimation of node location.MLPLS has strong adaptability for complicated deployment environment,and overcomes the shortage of traditional multihop algorithm which is only suitable for isotropic networks.Simulation results show that ML-PLS algorithm has high estimate precision and stable performance,and can adapt to different network environments.

multihop localization;wireless sensor network;partial least squares

TP393.08

A

1672-755X(2014)03-0019-07

2014-09-11

金陵科技学院博士启动基金(jit-b-201411)

窦如林(1979-),男,江苏南京人,实验师,硕士,主要从事无线传感器网和信息安全的研究。