制定铁路旅客票价的策略模型与求解算法研究

李树彬，党文修，傅白白

（1．山东警察学院治安系，山东 济南 250014；2．山东建筑大学交通研究所，山东 济南 250101）

*交通运输专栏*

制定铁路旅客票价的策略模型与求解算法研究

李树彬1，党文修1，傅白白2

（1．山东警察学院治安系，山东 济南 250014；2．山东建筑大学交通研究所，山东 济南 250101）

城市间的多种运输方式存在着竞争关系，在给定需求下票价价格是各种运输方式的调节杠杆。本文提出了一个铁路旅客票价制定的双层规划模型。首先建立了一个描述用户多等级、路径多阻抗、多标准情况的变分不等式模型，并将其作为双层规划模型的下层模型，然后以铁路运营总收益为上层目标，建立了相应的双层规划模型，同时设计了求解此模型的基于混沌－修正投影算法的启发式求解算法。结果表明，本文提出的票价价格制定机制是合理的，有望为有关部门的定价机制提供理论依据。

旅客票价；双层规划；变分不等式；求解算法

高速铁路推动了我国经济的发展，也带动了城际间出行需求的激增，铁路作为城际间交通的主要出行方式之一，是承载城市间交通的主要载体，也是保证我国经济快速发展的主要力量。目前，国家大部制改革促使铁路运营走上市场化，由于现有的定价机制存在一定的盲目性，已经远远落后于时代的发展，因此必须研究市场经济条件下新的铁路旅客票价制定策略。

市场经济的主要特点之一就是存在竞争性，就铁路而言，在长远距离上存在航空运输的竞争，而在中短路又存在着公路运输以及私家车的竞争。在相对较长的一段时间内，各种运输方式中的基本因素（如舒适度、方便性、旅行时间、安全性等）都不会发生较大的变化，因此相对来说票价对客流需求变化具有较大的影响。

关于票价定价机制的研究，大体上分为城市间运输方式和城市内运输方式两个方面。城市内的研究主要集中在公交票价、轨道交通和拥挤收费等方面，如Ferrari［1］讨论了在弹性需求和能力约束的条件下城市交通网络的收费问题；Friesz等［2］讨论了空间价格平衡网络的城市交通票价设计问题；王敏［3］分析了地铁票价制定的相关因素；史若燃等［4］研究了在不同市场机制下，多种交通方式的定价问题；蒋金亮等［5］研究了低碳交通下快速公交的票价优化方法等。城市间票价制定问题的主要研究包括公路、航空和铁路三个方面。黄欢等［6］利用系统动力学研究了公路客运票价制定问题，陈林［7］建立了航空公司实行多级票价的经济数学模型，朱金福等［8］探讨了航空客运舱位控制和超售综合静态建模。铁路方面，四兵锋［9－10］、陈建华［11－12］、李树彬［13－14］等分别研究了市场经济条件下的不同铁路旅客票价制定的理论模型和算法。但上述研究都把旅客作为一个整体，假设旅客具有相同的需求，并没有在运输方式提供的服务上进行细化，比如个人价值观不同，对时间的偏重程度也不同等。本文将旅客划分为几个等级，从而更加客观地反应现实情况。首先研究多级别的旅客需求，构建了一个新的变分不等式作为下层模型，同时考虑铁路运营的最大化收益，构建了双层规划的上层模型，从而组成了铁路旅客票价制定的双层规划模型。上层模型保证了铁路运营部门的最大化收益，下层模型考虑到了旅客自身的出行费用最小。

1 城际间多模式用户选择的变分不等式模型

城市之间的交通相比于市内交通较为简单，因为路线是固定的，不存在路径选择问题，只有交通方式的选择。交通网络如图1所示，节点表示城市，弧线表示运输方式，运输方式一旦选定，路线也就确定了。

考虑到需求会随费用变动的情况，最终将在各种运输方式之间达到一种均衡状态，在这种状态下，同一等级的旅客选择任何一种交通方式的最小广义费用全部相等，并且小于或等于未被选中的交通方式的出行费用。

设交通网络G＝（N，ξ），N代表节点集合；ξ代表有向路段的集合；P表示OD对集合，因为没有路径选择问题，每个OD对的连接只有不同的路段n；pn表示连接OD对p的第n个路段（即第n种运输方式）；Rp表示连接每个OD对p的路段总数。

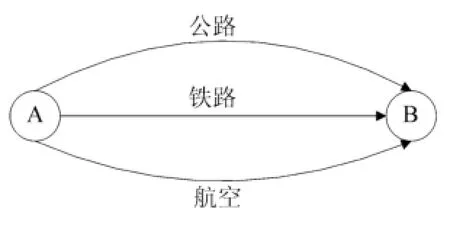
图1 交通网络图Fig.1 Three lines traffic network

将所有旅客划分为k个等级，每一级用i（i∈k）表示，那么表示pn路段上第i个级别的旅客流量表示OD对p的第i个级别的旅客流量，fp表示OD对p的所有旅客的流量。于是可以得出如下等式：

由于路段pn上每种交通方式所需要的时间基本上是固定的，所以流量与舒适度、安全度有一定的关系，通常这种关系是反函数关系：

其中，bpn表示交通方式pn的安全度舒适度。

本文假定非负参数和表示时间、票价和安全度、舒适度对第i级旅客的权重。权重越大说明对某种因素越重视。

lpn表示交通方式pn在某个OD对p之间的票价，用来表示pn上第i级用户的广义费用函数，一般是指数或者幂函数形式，本文设定如下：其中，q，b是待为标定的参数，tn是时间常数。于是，第i级别的旅客在交通方式pn上的广义出行费与总流量和票价有关。

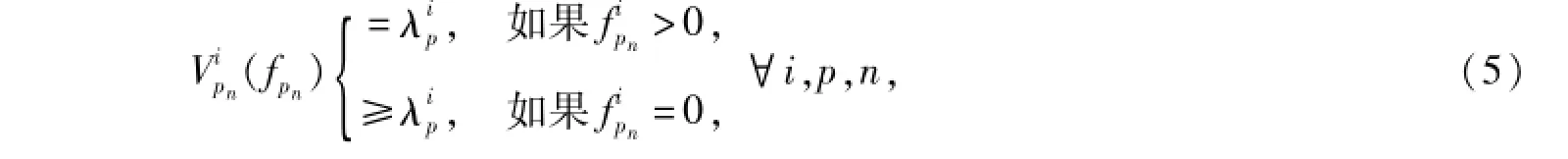
当我们固定其他交通方式票价时，满足上述条件的均衡问题可以表示成一个变分不等式：

这里〈…，…〉表示kn维欧几里德空间里的内积。

命题1上述变分不等式与所提出的均衡条件等价。

上述均衡条件与变分不等式等价，从均衡条件可以看出，对于固定的第i级用户的pn路段，可得

对（7）式中的OD对p的所有途径pn求和得到：

（8）式可以简化为

将（9）对p和i求和，可以得到下式

将其表示成向量形式，即可得（6）。

2 基于铁路运营收益的双层规划模型

变分不等式（6）描述了城市间多等级多标准的运输条件下，旅客从自身的利益出发，选择对自身来说出行费用最小的交通方式。因为各种交通方式由于价格的存在，出行费用也随价格而变动，因此铁路运营者可以通过改变票价来影响旅客在不同交通方式之间的选择，但不能决定旅客的最终选择，当然也期望自己的铁路经济效益最大。这就是典型的双层规划思想。

在这里，假设n＝1表示铁路运输，在某个OD对p之间铁路运输的客票价格为lp1，于是整个交通网络中，铁路运营的总收益为

其中Lp1表示铁路运输在OD对p之间每个旅客的平均客运成本。

在现有的经济体制下，政府部门由于考虑公益性，对铁路客票价格有一定的制约作用，那么票价必将有下限和上限：

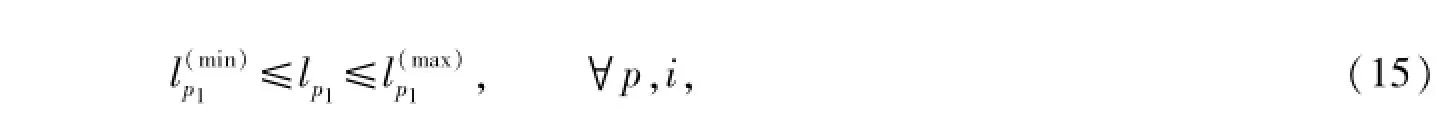
于是双层规划模型的上层模型如下：

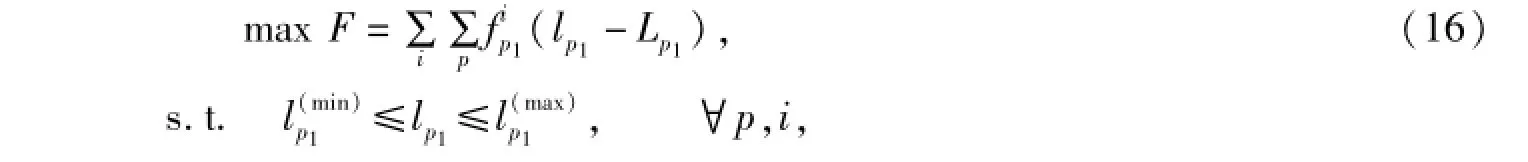
3 基于混沌－修正投影算法的启发式算法

对于上述双层规划模型当票价给定时，下层模型为一个变分不等式题，可用修正的投影算法进行求解［15］。鉴于混沌算法［16］的普适性，本文设计了一个基于混沌－修正投影算法优的启发式算法，其基本步骤如下：

（1）算法初始化。置k＝1，F*通常取一个较小的数。

（2）随机产生上层规划的变量lp1的初值，并将这个随机数变换到该优化问题变量的允许解空间。

（3）将上步的初始值代入到下层规划，利用修正的投影法求解下层变分不等式，得到最优解。

（4）将求得的值返回到上层规划，利用混沌优化方法对上层规划求解得到最优解及相应的最优值Fk。

4 数值算例

弹性需求问题往往可以用增设虚拟路段的方式加以解决［12］，由于双层规划模型求解的复杂性，本文采用固定需求的形式，并且只考虑了一个OD对，两种级别的旅客和两种交通方式，见图2（n＝1为铁路，n＝2为公路）。

图2 两级交通网络图Fig.2 Two lines traffic network

表1 已知费用数据Table 1 The known cost data

表2 模型参数值Table 2 Model parameter value

表3 模型所得结果Table 3 Model acquired results

上述结果表明，经过本文所提模型和算法的最优求解，合理的票价制定价格是26.96，此时存在两种交通方式的费用，其一为铁路运营，其二为公路运营，通过求解双层规划模型，两种运营方式的费用分别为65.54和59.4。费用不同是因为不同级别的旅客对不同属性的重视程度不同而引起的。从铁路运营的最大收益来说，此时票价价格既保证了旅客的出行费用最小，同时又满足了铁路运营的最大收益。通过模型的求解26.96是双层规划模型的平衡点，这表明，在双层规划思想的驱动下，两种运营方式的有条件博弈，最终达到了一个平衡点，即是最优的需求点。

5 结论

本文根据旅客对运输方式不同属性的偏好，将旅客划分为不同的等级，并运用均衡思想，建立了多级别多标准的均衡配流变分不等式模型。由于铁路运营者期望收益最大，但也只能用票价杠杆来调节需求的分配，不能最终决定旅客的选择，而旅客同时也期望自己的出行费用最小，这看似矛盾的组合体恰好符合双层规划的思想。因此本文中，建立了一个描述上述问题的双层规划模型，鉴于模型的求解复杂性，本文设计了基于混沌—修正投影算法的启发式求解算法，该算法避免了灵敏度分析所带来的求导困难，结果表明模型和算法是可行的，该模型稍加修改也可应用于其他的交通方式。本文的不足之处是算例偏小，并且没有将同一种运输方式进行细致划分，比如铁路上的高铁、动车、快车等，这也是下一步工作的方向。

［1］FERRARIP．Road pricing and network equilibrium［J］．Transportation Research，1995，29（3）：357－372．

［2］FRIESZ T L，HARKER P T．Multicriteria spatial price equilibrium network design：Theory and computational results［J］．Transportation Research B，1983，17（5）：411－426．

［3］王敏．地铁票价制定相关因素分析［J］．铁道运输与经济，2011，33（9）：6－8．

［4］史若燃，李志纯．不同市场机制下多种交通方式定价模型研究［J］．交通运输系统工程与信息，2010，10（5）：91－97．

［5］蒋金亮，宋瑞，刘杰．低碳交通下快速公交票价优化研究［J］．重庆交通大学学报：自然科学版，2011，30（4）：818－822．

［6］黄欢，蒋阳升，代漉川．基于系统动力学模型的公路客运票价制定［J］．交通科技与经济，2009（6）：22－25．

［7］陈林．航空公司实行多级票价的经济数学模型［J］．中国民航大学学报，2007，25（4）：40－43．

［8］朱金福，刘玮，高强．航空客运舱位控制和超售综合静态建模研究［J］．中国管理科学2006，14（5）：68－72．

［9］四兵锋，高自友．城市间公路客运的客票票价与其客流量之间的灵敏度分析［J］．中国公路学报，2000，13（2）：91－95．

［10］四兵锋，高自友．合理制定铁路客票价格的优化模型及算法［J］．管理科学学报，2001，9（1）：45－51．

［11］陈建华，高自友．多模式条件下需求变动时铁路客票价格制定的优化模型及算法［J］．交通运输系统工程与信息，2001，1（4）：319－330．

［12］陈建华．铁路旅客票价优化问题的相关模型及算法［D］．北京：北京交通大学，2007．

［13］李树彬．铁路旅客票价制定及其相关问题研究［D］．北京：北京交通大学，2007．

［14］李树彬，陈峰．城市间多模式交通旅客票价制定的博弈分析［J］．铁道运输与经济，2006，28（3）：8－10．

［15］任华玲，高自友．动态交通分配中一种离散VI模型的算法研究［J］．土木工程学报2004，37（3）：105－108．

［16］滕春贤，李智慧．二层规划的理论与应用［M］．北京：科学出版社，2002：84－92．

Strategy model and solution algorithm of railway passenger ticket price

LI Shu-bin1，DANG Wen-xiu1，FU Bai-bai2
（1．Department of Public Security，Shandong Police College，Jinan 250014，China；2．Institu te of Traffic，Shandong Jianzhu University，Jinan 250101，China）

Competition exists in multiple intercity transportation means．Ticket price is the adjustment lever for the given requirements．This paper presents a bi-level programming model for railway passenger ticket pricing．We initially construct a variational inequality model that can represent multi-class，multi-path cost and multi-criteria．It serves as the down-level model of the bi-level programming model．We then establish the up-level model of the bi-level programming model with total railway income as an object．We also design a chaos-modified projection algorithm based heuristic algorithm to solve a bi-level programming model．Results show that the proposed ticket pricing mechanism is reasonable．It will provide a better theoretical basis for government railway ticket pricing mechanism．

railway passenger ticket price；bi-level programming；variational inequality；solution algorithm

U293.1

A

1002-4026（2014）01-0073-05

10.3976／j.issn.1002－4026.2014.01.013

2013-03-13

国家自然科学基金（71171124）；山东省超级计算科技专项项目（2011YD01104）；交通运输部行业联合科技公关项目（2009-353-337-480）

李树彬（1977－），男，博士，研究方向为交通运输系统分系统与集成、智能交通等。