基于双目立体视觉技术的人体扫描系统的设计
宋昌江,吴 冈,姜 洋
(1.黑龙江省科学院自动化研究所重点实验室,哈尔滨150090;2.黑龙江省科学院高技术研究院,哈尔滨 150020)
伴随科学技术的迅猛发展,科学技术产品也逐步改变人们的生活。20世纪90年代兴起的基于计算机视觉的物体扫描技术得到了广泛的应用并受到人们的认可。以相同原理设计非接触式的三维人体扫描技术,秉承测试速度快、测量精度高等特点,在服装设计与生产、人物造型、医疗、艺术等领域,实现了人们对于个性化、高效率的需求[1]。
对于人体的非接触扫描的研究由来已久,其目的是为了获取准确、完整的人体点云数据[2]。这些方法之中,被人们所熟知的是激光扫描,该方法是目前光学式扫描的主要方式,具有较好的市场反响。与之相比,基于双目立体视觉技术的扫描方法,通过以二维图片代替一维激光束的方式,在保证扫描精度的同时,大幅度缩短了扫描的时间。要求“活体”静止是不可能实现的,只能通过最大限度地缩短扫描的时间来确保对人体的还原度,并且采用对人体完全无害的白光用于人体扫描更为适合。
1 系统设计原理
1.1 双目立体视觉技术
双目立体视觉[3],是计算机视觉技术的关键技术之一。其基本原理是利用两台具有位置差异,但具有相同结构和性能的CCD相机,同时获取被测物体图像,通过位置视差,即空间中同一物点在两幅图像中对应不同的像点,通过这对对应点位置差异和内在联系来重构该物点。如图1所示,对于空间物体表面任意点P,设C1摄像机获得的点P的像素点为pl。在OlP连线上任意一点P'的图像都是pl,因此仅由pl点,无法确定P的位置。但是,如果用两台摄像机同时获取点P,分别记为pl、pr。则P点既位于Olpl上,也位于Orpr上,即为两直线的交点,而唯一确定[4]。

图1 双目立体视觉原理图Fig.1 The princip le of binocular stereo vision
假设已知该任意点P在两个摄像机C1和C2上的像素点pl和pr,再假设两摄像机C1和C2的摄像机已标定,即已知两摄像机矩阵M1和M2,则有
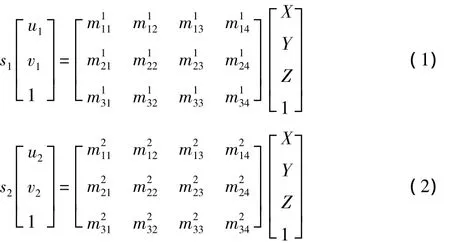
其中,(u1,v1,1)T和(u2,v2,1)T分别是pl和pr点在各自图像中的图像齐次坐标,(X,Y,Z,1)T为点P在世界坐标系下的齐次坐标,M1和M2为3×4矩阵,S1和S2为任意非零常数。联立式(1)和式(2),消去S1和S2可得

由上述可知,如果相机的内外参数已知,(一般可通过摄像机标定确定),对应点匹配的准确性将直接影响双目立体视觉方法的准确性。
1.2 对应点的约束
在一副对应的图像中搜索对应点,可简单比拟为在二维坐标系下确定一个点,即通过两条相交的直线。这两条“直线”就是两个约束。如图1所示,lr可表示为

其中
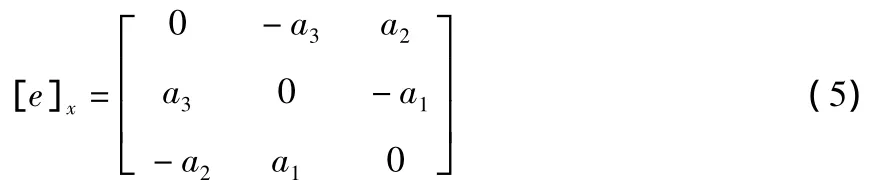
由射影几何原理,存在一个2D单应H矩阵,该矩阵的秩为3,满足Pl映射到Pr,即

由式(4)和式(6),可得

故定义基本矩阵F=[er]xH。
当系统满足双目立体视觉原理,则对应点存在基本矩阵关系,通常称这种关系为极线约束。
1.3 相位约束
双目立体视觉只提供了一个约束,另一约束需要通过其他方式获得。在以往的研究中,采用传统图像处理的方法居多,比如Candy算子、Sift算子等。这些方法的特点是匹配速度快,但精度较低。如果被测物体为规则形状,具有较好的效果。但对于形状复杂,特别是人体,由于图像与图像间匹配精度不高,匹配的对应点对数量不足等原因,经常导致扫描重构失败。因此,需要讨论新的方式。本文引入相移技术,通过对被测物体的相位展开,提供独立的相位约束。有关相移技术的基本原理这里就不多赘述,直接引用结果[5]。
这一约束就是一个相位解包裹的过程,目的是获得分布连续的位相值。计算一个周期内,即在0与2之间的位相值,将相位值进行展开。利用在0到2之间的位相值的正切函数从定义域到值域之间存在的非一一对应的映射关系,即不同相位值的正切值可能是差异,这样反正切函数只能取主值,从而使相位解包裹。
图2(a)为例,计算的相位值是不连续的。我们可以看到,必须有一个非常不连续的步骤。通过相位解包裹,我们将得到一个连续的阶段,如图2所示(b)。
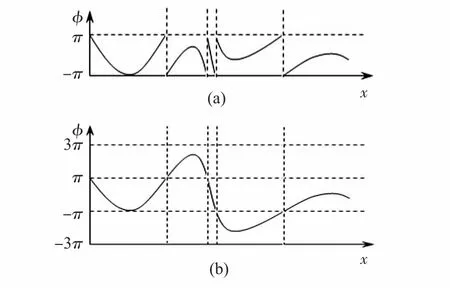
图2 相位和相位解包裹后Fig.2 Phase and phase after unw rapping
2 系统实现
2.1 对应点匹配实现
双目立体视觉的关键在于对应点的匹配精度。本文设计的搜索对应点的流程如图3所示。
第一步:以左图像点pl为例。计算该点相位值φ1,通过基本矩阵计算该点对应的右图中极线l2。
第二步:在l2中寻找点p21、p22,满足 min{|φ1- φ21|+|φ1-φ22|}。

图3 匹配算法流程图Fig.3 Matching algorithm
第三步:在右图中,以p21、p22为对角线的正方形区域内,采用重心法计算亚像素点p2。
如此往复,直至计算出所有所需的对应点对。
2.2 系统设计
依据由于本文系统设计原理,硬件主要设备采用:加拿大PiontGrey公司的FL3-GE-13S2C-C彩色数字CCD相机,该相机分辨率为1 288×964;韩国LG公司的LG50投影机,系统结构由自主设计完成。采用双目立体视觉的方法设计系统,对系统硬件的空间关系要求不苛刻,首先需要两个摄像机成一角度,且这个角度小于90°,为了设计简便,则将两摄像机成同一水平放置,固定在一个机架上。其次需要投影机投出的光栅图像的范围略大于摄像机采集的范围,使得摄像机所采集的图像为被光栅完全覆盖范围,且两摄像机所采集图像信息尽可能的重叠,以保证较大的测量范围,因此投影机与水平方向放置的摄像机成一定的角度。这就是本文测试部分的基本要求。为一次性获得闭合的人体点云,本文采用4组系统,同时工作的方式,如图4(a)分别为单组和如图4(b)4组系统的实物图。

图4 系统样机实物图Fig.4 The prototype object
2.3 实验结果
通过自主研发的软件,对人体模特扫描可得结果如图5所示,分别显示扫描结果。
通过对一组标准量块的测量,验证本文设计方法的精度。测试量块选择哈尔滨量具刃具厂生产的型量块,符合GB/B6093-2001标准3级,选定的量块分别为400 mm、500 mm。如表 1 所示,测量误差为 0.54 mm、0.63 mm。

图5 过程和结果图Fig.5 The process and results
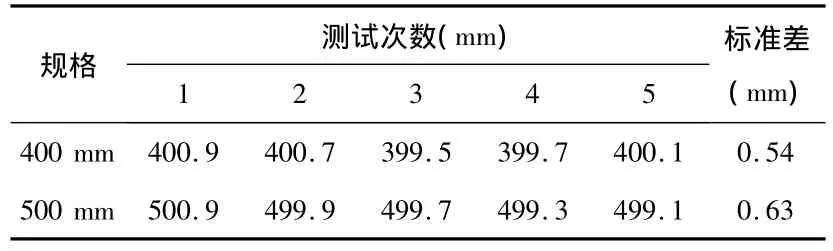
表1 标准量具测试表Tab.1 Standard measuring test
由于本文采用视觉方法,因此在较长时间内的实验测试中,受光线强弱的影响比较明显,但实验数据表明,本文系统样机能够保证测试精度的稳定性和系统精度,误差都小于1.0 mm。由于被测人体差异,测量的计算时间略有不同,进行一次测量的投影时间为16 s,计算时间在16~20 s。
3 结论
本文讨论了双目立体视觉技术在人体扫描中的应用。通过对双目立体视觉技术特点分析,方法的设计和基于相移约束的对应点匹配的研究,实现了对人体快速、低误差的扫描。最终测试扫描人体的误差低于1 mm。采用对人体无害的白光,在16~20 s的测试时间内,能够达到这一指标,对于人体的扫描有着十分重要的应用价值。
本文是对双目视觉系统在人体扫描工作中的尝试性应用研究,虽然获得较好的效果,但在系统标定、点云拼接等方面还需要不断深入研究和完善。
[1]陈益松,夏明.光学三角测量法及其在人体测量中的应用[J].纺织学报,2012,33(12):95—101.
[2]林琳.投影光栅法三维人体重构研究[D].上海:东华大学,2009.
[3]P.F.LUO,S.S.LIOU.Measurement of cured surface by stereo vision and analysis[J].Optics and Laser in Engineering,1998,(30):471—486.
[4]JANNE HEIKKILÄ,KUMPULAINEN.Second order initial value problemswith non-absolute integrals in ordered Banach spaces[J].Nonlinear Analysis,2011,11(3):1138—1156.
[5]GOODALL A.J.E.,BURTON DR.,LALOR M.J.The future of 3-D range image measurement using binary-encoded pattern projection[J].Optics and Laser in Engineering,1994,(21):99—110.

