聚类分析方法在济宁市水质分析中的应用

刘 铭，朱长军，顿珠加措，尼玛次仁

（1.河北工程大学城建学院，河北邯郸 057150;2.西藏自治区水文水资源勘测局日喀则水文水资源分局，西藏日喀则 857000;3.西藏自治区水利电力规划勘测设计研究院西藏拉萨 850009）

水质评价是指按照评价目标，选择相应的水质参数，采用相应的水质标准和评价方法，对水体的质量利用价值及水的处理要求做出评定，使用广泛的常规环境质量评价方法大致分为综合指数法、数理统计法、分级评价法和其他方法四大类［1］。在复杂的环境系统中存在很多模糊性，例如环境影响的“大”与“小”、污染物浓度的“高”与“低”、方案的“优”与“劣”等均无法用确定的界限加以划分［2］。在对区域水环境质量进行水质评价时，仅将综合指数评价法应用于环境质量综合评价，其理论方法和实际结果存在着一定的缺陷，往往难以实现对区域水环境的总体评价。目前，聚类分析法已被广泛应用于环境质量评价中，聚类分析方法能够较好评价生物指标，综合考虑生化指标，有助于合理评价水质分布与特性［3］;通过聚类分析能确定海域主要污染指标和污染程度，能够较合理地反映海域的环境质量特征［4］;许多土壤研究者与环境工作者运用聚类分析在土壤质量评价中开展了卓有成效的工作［5］。大量的研究结果表明，多指标存在时应用聚类分析方法能够对环境质量做出更为客观、准确的综合评价。本次水质分析采用聚类分析的统计方法，通过对水质监测监测数据的统计分析，研究比较各监测站点水质指标数据的相关关系，对具有相近数据关系的监测站点进行归类，另外结合监测站点水质综合评价结果和区域内地理位置及当地水污染实际情况，从而对区域水环境质量做出总体初步评价。

1 监测站点资料

济宁市位于山东省西南部，京杭大运河穿过济宁市，素有“运河之都”的美誉，我国北方最大的淡水湖南四湖也位于其中。随着城市的发展，济宁市水污染情况越来越严重，同时南水北调工程的启动也对济宁市的水质提出严格要求。济宁市内河流纵横分布，各段污染状况不同，水质监测站点的布点也因此密布整个济宁市而且数量较多，这最终导致水质评价时会出现繁杂等困难。本次分析选取济宁市水质监测数据，共选取包括25个地下水监测站点的水质监测结果，选取C1、SO4、总硬度、BOD5、CODMn、氨氮、亚硝酸盐氮、硝酸盐氮、酚共9项水质监测指标，济宁市监测站点区域分布见下图1，各个监测站点水质监测数据见表1:

表1 监测站点水质监测数据Tab.1 The water quality monitoring data from monitoring sites

2 聚类分析与综合评价

2.1 监测站点的聚类分析

聚类是按照某个特定标准把一个数据分割成不同的类或簇，使得类内相似性尽可能的大，同时类间的差异性也尽可能的大［6］。聚类分析方法的基本思想是研究对象之间存在着不同程度的相似性，通过分析比较各事物之间的性质，将性质相近的归为一类，将性质差别较大的归入不同的类，聚类分析中常见的有系统聚类法和K均值聚类法。本次数据分析选用系统聚类法，这是目前实践中使用最多的，该方法的分析步骤是:先将所有样本看成一类，选用一定的方法计算样本与样本之间的距离和类与类之间的距离;开始，每个样本自成一类，类类之间和样本之间的距离相同;然后，在所有的类中选择距离最小的合并为一个新类，并计算出其与其它类的距离;接着再将距离接近的类合并，直至将所有样本合并为一类为止。由聚类系谱图可以清楚的看出全部样本的聚集过程，进而做出样本的分类。

由于水质各项指标监测数据存在计量量纲的不同，数值大小差异较大，因此需要首先对数据进行标准化处理，本次选用极差标准化法处理数据。假设有m个聚类对象，每个对象有n个要素构成，其所对应要素数据如表2所示。

表2 聚类对象与要素数据Tab.2 The clustering objects and data elements

极差标准化公式如下:

式中Xij为监测指标原值，其中1≤i≤m，1≤j≤n为标准化后数据;为监测指标的最小值;为检测指标的最大值。

经过标准化处理所得的数据，极大值为1，极小值为0，其余的数值均在0与1之间。

系统聚类分析的依据和基础是数据之间的差异性，差异性的测度即为距离的计算，距离较大则样本相似性越小。距离的计算有多种选择方法，本次选用Pearson相关性来计算各样本之间距离。

系统聚类的过程中类与类之间距离计算方法可以分为单连接法、完全连接法、平均连接法、组平均连接法和离差平方和法等，本次计算类与类之间距离选用组平均连接法，该方法采用的距离定义为两类之间的平均平方距离，如下:

根据选取的济宁市各个监测站点得到水质监测数据，利用统计分析软件SPSS进行聚类分析计算，计算过程如下:

（1）用极差标准化方法对各水质指标的原始数据进行处理;

（2）采用Pearson相关性测度监测站点之间的样本间距离;

（3）选用组平均法计算类间的距离，并对样本进行归类。

经过上述聚类个步骤方法的选择得到聚类的结果如图2示:

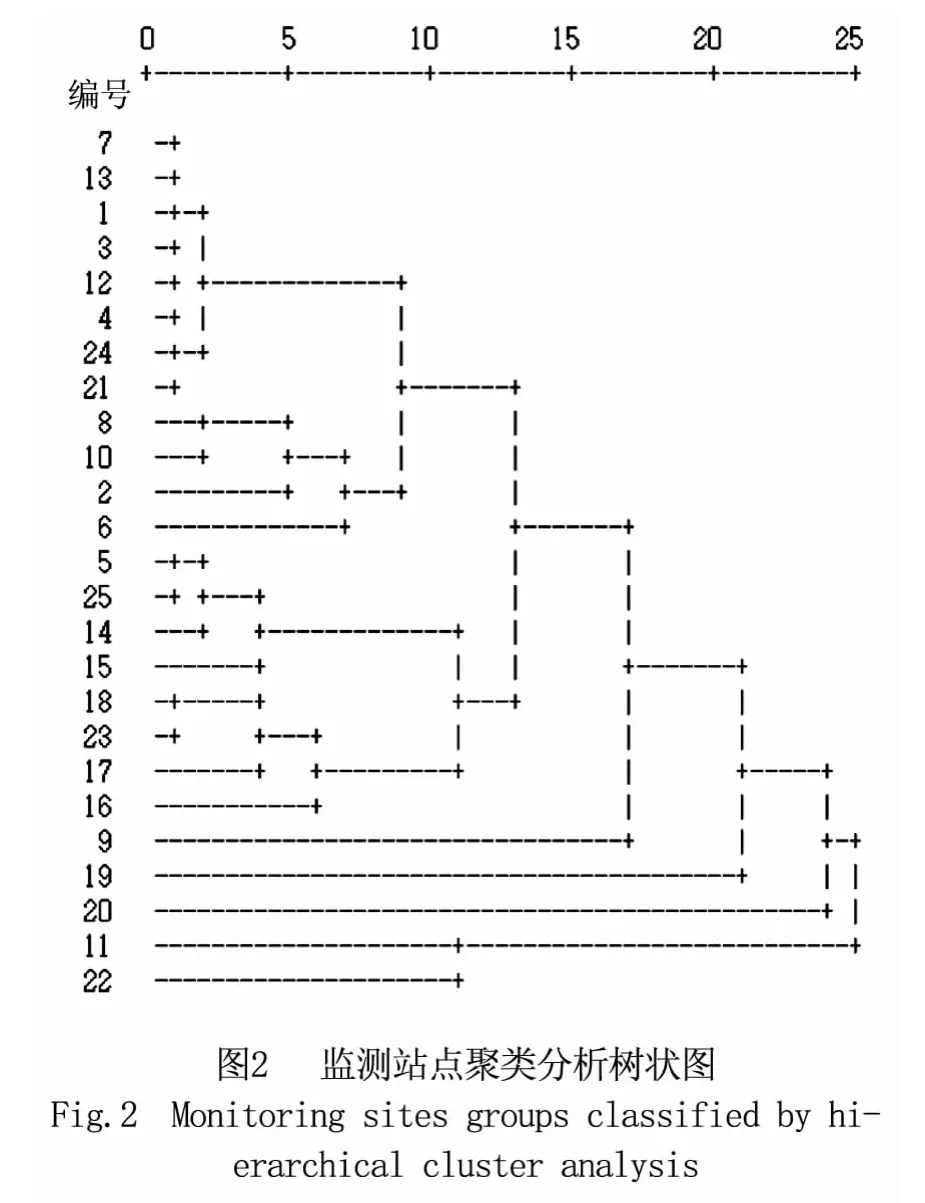
SPSS软件聚类分析所得的树状图能够清楚显示出这些监测站点的聚类过程，同时根据聚类分析树状图的结果，能够将监测站点分为六类，具体监测站点分类如下，第一类监测站点编号:7、13、1、3、12、4、24、21、8、10、2、6;第二类:5、25、14、15、18、23、17、16;第三类:9;第四类 19;第五类:20;第六类:11、22。

2.2 监测站点的综合评价

采用内梅罗综合指数评价法，计算各监测站点的综合指数。首先进行单组分评价，划分组分所属质量类别，对各类别按表3分别确定单项组分评价分值Fi，然后代入内梅罗综合指数评价公式计算综合评价分值F，根据F值，按照表4划分地下水质量级别。

内梅罗综合指数评价法公式:

2.3 监测站点分类

经过聚类分析，济宁市的监测站点一共分为六大类，用综合指数法计算各监测站点的污染级别，最终将二者数据相结合，各监测站点所属类别及分布区域和污染级别如下表5所示:

3 结论

（1）第一类包括12个监测站点，24号及21号分布于中山区外，其余均分布于任城区，水质综合评价级别除2号为IV类外其余均为II类，对2号监测站点水质数据分析知，其酚类污染物属国家IV类标准，导致其水质级别较差;

（2）第二类包括8个监测站点，其中3个分布于任城区，5个分布于市中区，水质综合评价级别均分布于III－V类，由监测站点数据分析知，25号、17号及5号、15号、16号监测点均是由于总硬度超出IV、V类标准，因而水质级别较差和极差;

（3）9号、19号各为一类，分别位于任城区和市中区，虽然综合评价级别均为良好，但由监测数据可知其主要污染类别不同，19号其氯化物以及硝酸盐氮量明显高于9号;

（4）20号自成一类，位于市中区，其主要污染物是亚硝酸盐氮，其含量超出国家V类标准;

（5）11号和22号分别位于任城区和中山区，均系酚类超出国家V类标准，因而分为一类，而22号由于硝酸盐氮属V类标准，导致水质较差。

通过聚类分析法对监测站点的分类结果看出各类间的主要区别在于水质污染级别的不同或是主要污染因素的不同，结合各个监测站点以及污染源分布图可以得出:市中区总体水质质量较差，其主要原因是市区内人口以及工业企业密集分布，污染排放量大;任城区一些高污染排放企业周围水质较差外，其他地区水质良好，这与任城区河流分布较多是分不开的，污染物排放后会随河流流入湖泊，从而减轻了其对地下水污染的影响。

表3 单项组分评价分值Tab.3 Single component evaluation

表4 地下水质量划分级别Tab.4 Groundwater quality grade

表5 综合评价与聚类结果Tab.5 Results of comprehensive evaluation and clustering

［1］熊德琪.环境系统模糊集分析理论与应用［M］.大连:大连海事大学出版社，2001.

［2］马风才.项目环境影响模糊评价理论与应用研究［D］.北京:北京航空航天大学，2001.

［3］曾淦宁，吴国权，徐晓群.多元聚类分析方法在杭州湾水质分析上的应用［J］.浙江工业大学学报，2009（1）:14－19.

［4］罗薇，邵秘华，周立新.聚类分析功能在大连港水域环境质量评价中的应用［J］.大连海事大学学报，2004（4）:51－55.

［5］蔡瞳，徐惠，吴群.土壤质量聚类分析—以封丘县为例［J］.安徽农业科学，2008，36（25）:10998－10999.

［6］顾洪博，张继杯.不确定数据的聚类分析研究及应用［J］.河北工程大学学报:自然科学版，2012，29（1）:109－112.