基于动网格的地铁活塞效应非稳态气流模拟

由世俊，薛 鹏，张 欢

基于动网格的地铁活塞效应非稳态气流模拟

由世俊，薛 鹏，张 欢

(天津大学环境科学与工程学院，天津 300072)

活塞效应是影响地铁隧道和站台气流非稳态流动的主要因素，为此采用现场试验和数值模拟的方法对气流进行分析．其中，实验选在装有安全门的运行车站，并记录列车运行时的测点风速．数值研究基于实验车站的全尺寸模型，并利用动网格技术对其模拟．研究结果表明，采用标准k-ε方程的模拟方法结果和实验数据吻合较好，证明其适用于高雷诺数的隧道模拟研究．研究同时发现，活塞风在站台前后两个联接处(迂回风道和活塞竖井)中表现出比较稳定的分流和吸风比率，且无论在开式系统还是闭式系统状态下，进入迂回风道和吹入站台的风量是成特定比例关系的．

标准k-ε方程；活塞风阀；迂回风道；全尺寸模型；分流比率

随着城市地铁的快速发展，人们越来越关注地铁车站的环境，包括空气温度、湿度、速度、压力及噪声等．为人们提供舒适和健康环境的地铁车站的环控系统很大程度上受到由列车引起的活塞效应的影响[1]．

许多学者对地铁活塞效应引起的非稳态流动有所研究，Wang等[2]用理论方法研究了活塞效应．Bao等[3]通过FLUENT数值计算验证了活塞效应的形成过程．Kim等[4-5]通过数值模拟分析了竖井位置对通风能力的影响．Lin等[6]通过SES分析了活塞竖井的长度对隧道通风的影响．Juraeva等[7]通过CFX分析隧道热风幕安装的相对最佳位置．Huang等[8-9]通过FLUENT分析隧道中的气流，并分析了竖井数量和位置对隧道通风的影响；此后他对首尔的实际车站进行了模拟分析，并将结果与1∶20的模型实验数据进行对比．但是缩小模型和实物很难保证雷诺数和格拉晓夫数的一致[10]，所以对于地铁数值模拟研究最可靠的就是用现场的实验数据进行验证．

在我国北方的大部分城市，地铁站台经常使用全高安全门系统，这会留出0.5,m高的空间使隧道和站台之间进行气流交换[11]．如果合理利用这部分气流交换，不仅可以提高站台内的空气质量和舒适度，还可以达到一定的节能效果．Jia等[12]用数值方法研究了气流在隧道和车站内的特性．Ke等[13]结合SES和PHOENICS优化设计了地铁环控系统．当带有活塞竖井和安全门的车站物理模型得到验证后，使用数值方法研究车站的非稳态气流特性得到的结果可以代替实验作为研究分析的依据．

笔者主要研究地铁活塞效应带来的非稳态气流对车站环境的影响．本文根据沈阳地铁1号线太原街站的图纸建立全尺寸的物理模型，列车的进站、停靠、出站的运动过程利用数值模拟的方法进行模拟；模拟结果用现场实验测试的数据进行验证；进而分析活塞风在隧道与迂回风道和活塞竖井联接处的气流分流比率及吸风比率．

1 实验方法

沈阳地铁冬季采用闭式系统(活塞风阀关闭)，夏季采用开式系统．由于地铁的活塞效应会影响到整个车站，尤其是车站出入口和活塞竖井．本实验在太原街站布置了几个测点，目的是测量列车运行对车站出入口和活塞竖井的气流影响．

实验选择的太原街站位于地铁线路中段，属于典型车站．站台层长114,m，宽9.8,m，高5,m；站厅层长94,m，宽17.3,m，高5,m．区间隧道宽度为5.4,m，站台两侧隧道宽3.75,m．沈阳地铁列车由6节车厢组成，共长118,m．车头的迎风面积为8.82,m2(宽2.8,m，高3.15,m)．太原街站在车站两头各有一个活塞竖井，竖井高5,m，宽5.2,m，竖井顶部的百叶窗通风面积为20,m2．站台屏蔽门的高度为2.5,m，车站出口的尺寸与工程图纸相同，具体物理模型如图1所示．

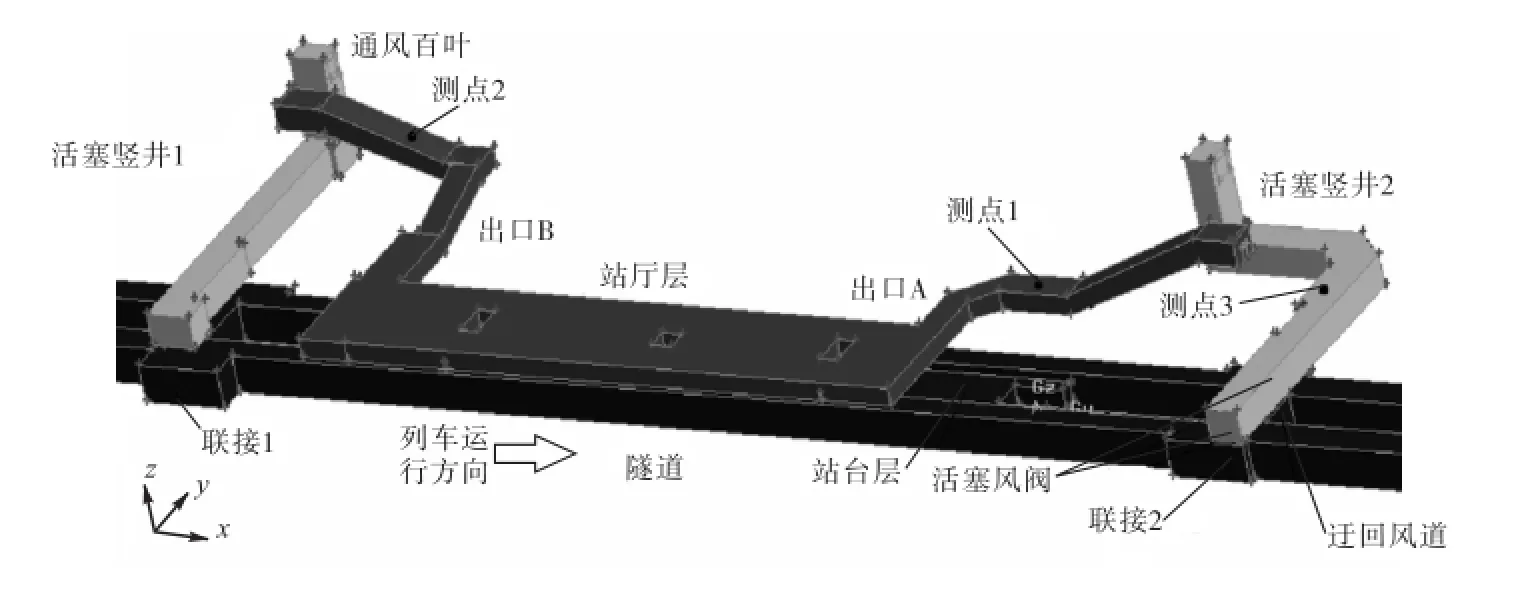
图1 太原街站的物理模型Fig.1 Geometrical model of TYJ station

实验测量时，活塞风阀全部打开．风速的测量利用高精度多功能TSI Q-Trak．热球传感器的误差范围为±0.02,m/s，计数周期为1,s．活塞风阀至通风百叶的距离为82,m．活塞竖井2的布局如图1右侧，在距活塞风阀30,m处标出了测点3．出口A和B与站厅的距离都为65,m，测点1和2也都设置在距离出口30,m处．每个测试点平行放置3台仪器，测点高度均为1.5,m，并设置在直管段，降低气流漩涡等因素带来的干扰．实验时间为14：00—17：00点，车站人流避着测量仪器行走且密度较小，故忽略客流对测点1和测点2的影响．实验装置如图2所示．

实验时，测试人员分为4组：2组分别测出口A和出口B的风速；1组测活塞竖井的风速；1组记录列车进站和出站的时间．实验中所有的设备均在测试前进行时间校准．其中，定义列车进站时间为列车停站的时间点；出站时间为列车启动离站的时间点．

图2 出口实验装置Fig.2 Measurement setup for exit

2 数值方法

2.1 假 设

活塞效应是引起非稳态湍流的主要因素，为对气流进行定量分析，做以下假设：

(1) 在模拟中，只考虑1辆列车的行驶，不考虑隧道对面来车的共同作用；

(2) 活塞效应是唯一影响车站气流的因素，不考虑机械通风和人流的影响．

2.2 数学模型的设置

采用FLUENT6.3.26软件计算列车运行时的速度场和压力场，并采用连续性方程、雷诺时均-纳维叶斯托克斯和标准k-ε湍流方程进行求解．其相应的运输方程为

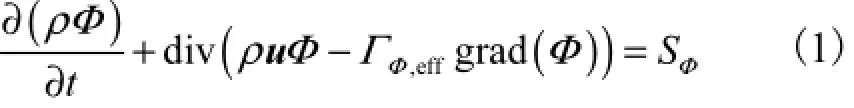
式中：Φ是通项，可以代表分速度矢量u、湍动能系数k、湍动能耗散率ε；ρ为气体密度，kg/m3；Γ为广义扩散系数；SΦ为Φ的源项．

笔者利用动网格技术来模拟列车的进站和出站过程．在FLUENT6.3.26中，有3种模型可以定义动边界：弹性光滑模型、动态分层模型和局部重画模型．考虑到列车的运动特性和大量的网格，经过试算，本研究同时利用后两种模型进行模拟．这样，列车运行的每一步动态结果将由FLUENT在每个时间步长内通过调整网格来计算．

网格划分采用非结构化四面体网格，隧道网格间隔设置为0.3,m，列车边界设置为0.2,m，车站设置为0.4,m，活塞竖井设置为0.5,m，网格总数为453.2× 104，时间步长为0.005,s，总模拟列车运行时间为110,s．列车的初速度为20.68,m/s，持续1,s．此后列车减速运动，减速度为0.94,m/s2，持续22,s直至列车停站．期间列车运行距离为248,m．列车停站63,s后，加速驶离车站．加速度为0.83,m/s2并在运行24,s后达到19.92,m/s，运行距离239,m．这些边界条件被编译成用户自定义函数，读入到计算软件中．列车后方的隧道口被设为压力入口，其他所有的出口被视为压力出口．选用SAMPLE算法对速度-压力进行耦合求解，选用标准方法对压力进行矫正．密度、动量、湍动能的离散使用一阶方程．对于非稳态流动的分析，时间离散采用一阶隐式．

3 结果分析

3.1 数学模型验证

为验证数学模型的正确性，将3个测点的模拟数据同实验数据进行对比，如图3所示．其中，正值表示出风，负值表示进风；实验值是3次无对面来车实验的平均值．停车期间的实验及模拟数据集中表现在图中深色区域．

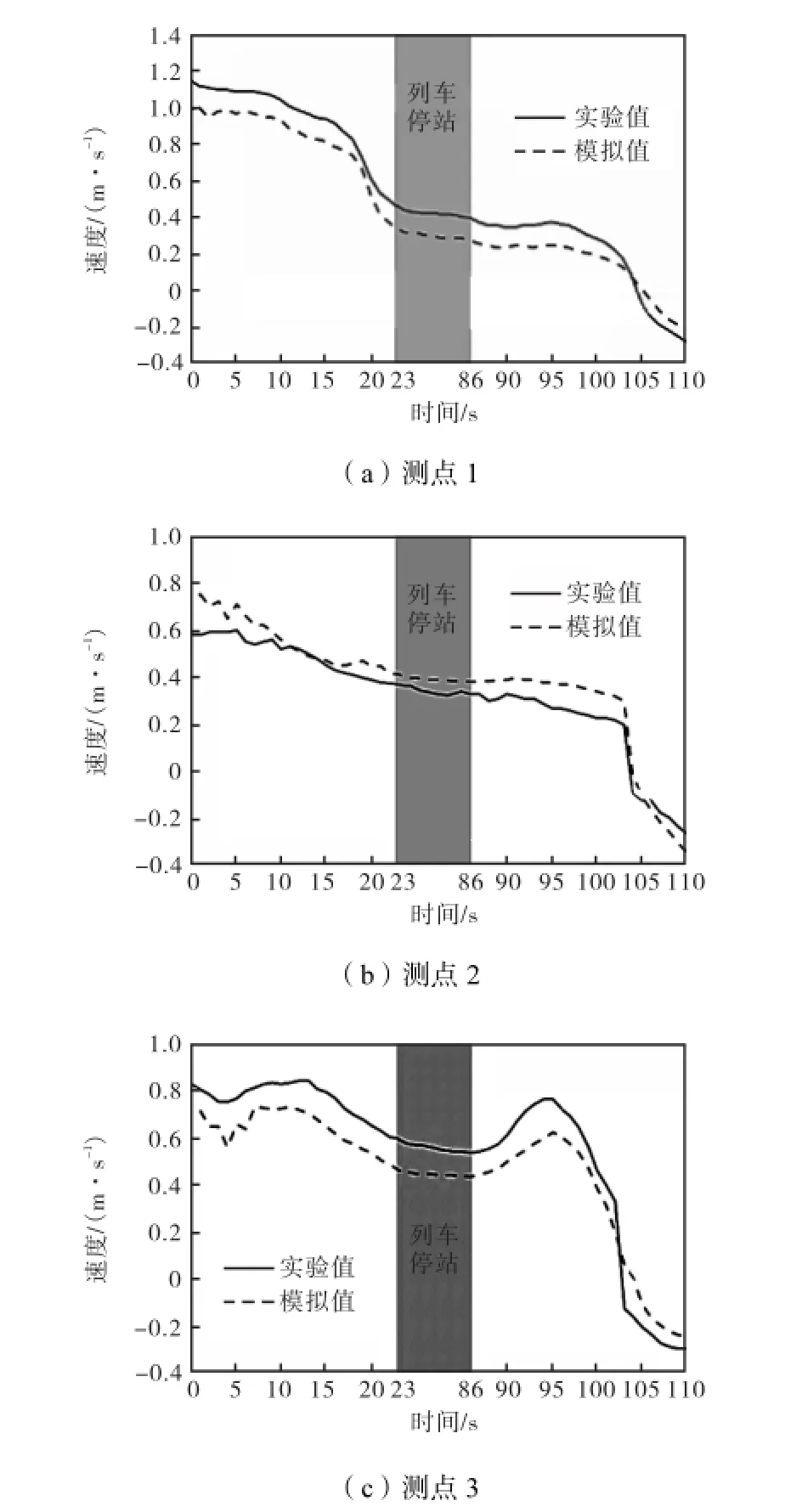
图3 测点的模拟值与实验值对比Fig.3Comparison between numerical and experimental results

如图3所示，数值计算方法能比较准确地预测风速随时间的变化趋势．在图3(a)和(b)中，出口流速随着列车的减速而下降．由于流体缓冲作用和列车启动时较小的吸风效果，出口风向在启动后20,s才改变．就平均速度而言，测点1模拟数据比实测数据小13.5%，测点2模拟数据比实测数据大12.5%．在活塞竖井中的测点3，模拟数据较好地吻合了实验数据．风向变化发生在列车经过活塞风阀的过程中，具体时间点为102.5,s．

通过以上对比，数学模型得到了很好的验证，说明标准k-ε方程适用于高雷诺数的地铁气流非稳态动网格模拟．

3.2 活塞风的分流比率和吸风比率

3.2.1 开式系统中的分流比率和吸风比率

当地铁运行时，活塞效应产生的压力波会将活塞风沿着隧道吹向站台，对站台空气造成很大的影响，如图4所示．

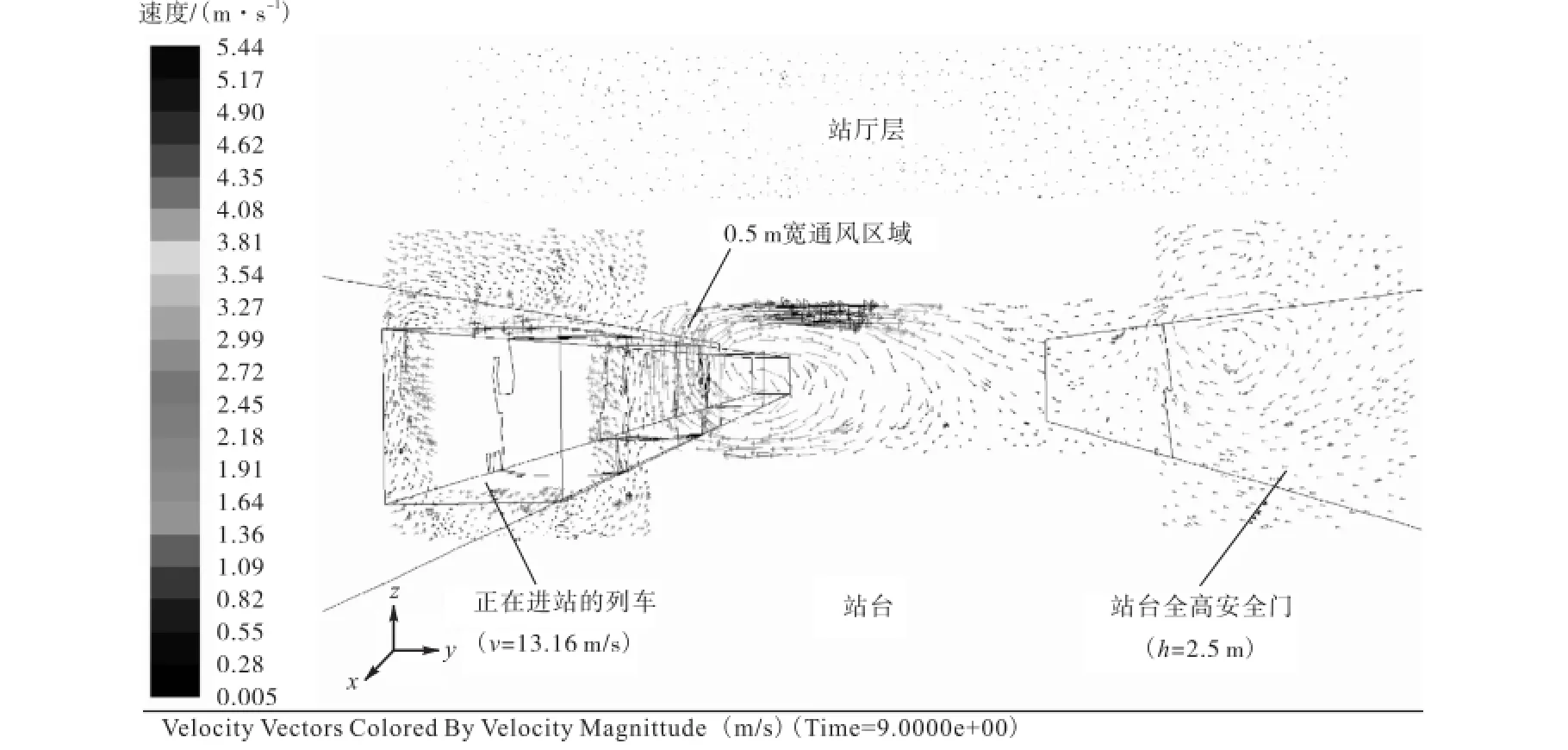
图4 活塞风对站台气流的影响Fig.4 Influence of piston effect on platform

图4 显示，在列车进站时(t=9,s)，由安全门上方进入站台的风速最高可以达到5.4,m/s，这将会造成人们的不舒适．所以在开式系统中，车站两头的活塞竖井和迂回风道承担了分流的作用．在开式系统中，活塞风在隧道联接处分流，流向竖井、迂回风道和站台方向．图5(a)为活塞风在联接1处的分流情况(t=5.4,s)．通往站台方向的风会分流到站台或留在站台隧道．与此相反，当列车离站的时候，列车尾部的负压会从竖井、迂回风道和车后隧道吸风．图5(b)为活塞风在联接2处的吸风情况(t=105,s)．图中列车沿x轴正方向运动．

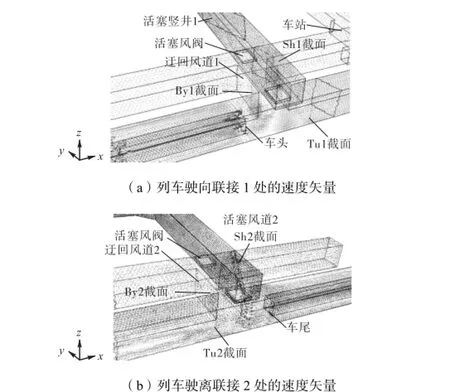
图5 联接处的物理模型Fig.5 Geometrical model of links in tunnel

将图5中标示出的各截面气体质量流量进行对比分析可得活塞风非稳态流动时在联接处的分流比率和吸风比率．各面流量结果如图6所示，其中流量以x轴和y轴的正方向为正．

如图6所示，整个地铁运行过程被分为7个时间段．需要说明的是，在停站时段4(23～86,s)中气流趋于稳态，用于分析分流比率的数据显示在图中前23,s，分析吸风比率的数据显示于后24,s．而由于气流的缓冲作用，流向站台的气流流量不能用出口的流量简单叠加，而是由流经Tu1和Tu2的流量进行计算，即

式中：,pmq为流向站台的气流质量流量，kg/s；,t1mq为联接1处流经Tu1面的质量流量，kg/s；,t2mq为联接2处流经Tu2面的质量流量，kg/s．

在时段1(0,s＜t＜6,s)中，列车向联接1处行驶，每个面的流量相关性很高．经过计算，在联接1处的活塞风量与分流比率见表1．图6中的点Ⅰ是列车头经过联接1的时间点，流向发生变化是因为车和隧道之间的间隙被反方向的气流占据．在时段2(6,s＜t＜17,s)中，列车通过联接1，由于列车减速和流体的黏性，活塞效应减小，车身表面的风速与列车同向，截面的气流方向也逐渐变为正向．点Ⅱ是列车尾部驶离联接1的时间点，列车尾部的负压区作用立刻体现出来．在时段3(17,s＜t＜23,s)中，列车驶过联接1并进站停车，随着列车减速，吸风作用随之下降．

图6 开式系统各截面的空气质量流量Fig.6 Mass flow rate of the each channel in open system

表1 时段1中联接1处的风量与分流比率Tab.1 Mass flow rate and diversion ratio of each channel in period 1

与此相似，在时段5(86,s＜t＜94,s)中，列车启动并驶向联接2，随着列车加速，吸风作用随之增加．点Ⅲ是列车头经过联接2的时间点，与点Ⅰ相同，流向发生了改变．在时段6(94,s＜t＜105,s)中，列车通过联接2，随着列车速度的增加，活塞效应变大，流量也越来越大．点Ⅳ是车尾驶离联接2的时间点，活塞效应的吸风作用充分表现出来，在此之后的时段7(105,s＜t＜110,s)中，列车驶离联接2并驶向下一站，随着车速的提高，吸风作用增加．经过计算，联接2处在此时间段中的吸风比率见表2．

3.2.2 闭式系统中的分流比率和吸风比率

我国北方地铁系统在冬季会采取闭式运行，这时活塞风阀全部关闭，起不到分流和通风的作用．闭式运行时各个截面的气体流量如图7所示，列车运行状态和开式系统相同．

由图7得知，在闭式运行时，迂回风道和进入站台的风量同时增加，趋势一致．在时段1中，活塞风量与分流比率见表1．在时段7中，活塞风量与吸风比率见表2.

由表2可以看出，闭式运行时各截面风量和吸风比率均有增加，但是分流通道之间的流量比例却相对稳定．其中分流时，迂回风道的风量始终是去站台方向风量的1.5～1.6倍，进入站台的风量是留在站台隧道风量的1.3～1.4倍；吸风时，从车后隧道吸入的风量是从迂回风道吸入风量的5.3～5.4倍，其中从站台隧道吸入的风量是从站台吸入风量的2.0～2.1倍．

图7 闭式运行和开式运行时各截面流量对比Fig.7 Comparison of mass flow rate of each channel in open and close systems

表2 时段7中联接2处的风量与吸风比率Tab.2 Mass flow rate and suction ratio of each channel in period 7

4 结 论

(1) 标准k-ε模型适用于由地铁活塞效应引起的高雷诺数非稳态气流动网格模拟．

(2) 在开式系统中，活塞风在站台前后2个联接处(迂回风道和活塞竖井)表现出比较稳定的分流比率和吸风比率．其中站台与隧道之间的换气量约为活塞效应引起通风量的20%．

(3) 在闭式系统运行时，活塞风阀关闭，其他通道的流量和比率较开式系统均有所增加．但通道之间的流量比例相对稳定．

［1］ Yuan Fengdong，You Shijun. CFD simulation and optimization of the ventilation for subway side-platform[J]. Tunnelling and Underground Space Technology，2007，22(4)：474-482.

［2］ Wang Feng，Zhi Fangyin. A study on subway tunnel ventilation for piston effects [C]// International Conference on Pipelines and Trenchless Technology. Shanghai，China，2009：910-921.

［3］ Bao Haitao. Study of piston wind in subway tunnel based on numerical simulation[C]// IEEE Computer Science and Information Technology. Huangshi，China，2010：266-268.

［4］ Kim J Y，Kim K Y. Experimental and numerical analyses of train-induced unsteady tunnel flow in subway[J]. Tunnelling and Underground Space Technology，2007，22(2)：166-172.

［5］ Kim J Y，Kim K Y. Effects of vent shaft location on the ventilation performance in a subway tunnel[J]. Journal of Wind Engineering and Industrial Aerodynamics，2009，97(5/6)：174-179.

［6］ Lin Chiji，Chuah Yew Khoy，Liu Chia-Wei . A study on underground tunnel ventilation for piston effects influenced by draught relief shaft in subway system[J]. Applied Thermal Engineering，2008，28(5/6)：372-379.

［7］ Juraeva Makhsuda，Lee Jun-Ho，Song Dong-Joo. A computational analysis of the train-wind to identify the best position for the air-curtain installation[J]. Journal of Wind Engineering and Industrial Aerodynamics，2011，99(5)：554-559.

［8］ Huang Yuandong，Gao Wei. A numerical study of the train-induced unsteady airflow in a subway tunnel with natural ventilation ducts using the dynamic layering method[J]. Journal of Hydrodynamics，2010，22(2)：164-172.

［9］ Huang Yuandong，Gong Xiaolu，Peng Yuejiao，et al. Effects of the ventilation duct arrangement and duct geometry on ventilation performance in a subway tunnel[J]. Tunnelling and Underground Space Technology，2011，26(6)：725-733.

［10］ Chen Q Y. Ventilation performance prediction for buildings：A method overview and recent applications[J]. Building and Environment，2009，44(4)：848-858.

［11］ Ogawa T，Fujii K. Numerical investigation of threedimensional compressible flows induced by a train moving into a tunne[J]. Computers & Fluids，1997，26(6)：565-585.

［12］ Jia Li，Huang Peng，Yang Lixin. Numerical simulation of flow characteristics in subway station[J]. Heat Transfer：Asian Research，2009，38(5)：275-283.

［13］ Ke Ming-Tsun，Cheng Tsung-Che，Wang Wen-Por. Numerical simulation for optimizing the design of subway environmental control system[J]. Building and Environment，2002，37(11)：1139-1152.

(责任编辑：赵艳静)

Numerical Simulation of Unsteady Airflow in Subway Influenced by Piston Effect Based on Dynamic Mesh

You Shijun，Xue Peng，Zhang Huan
(School of Environmental Science and Engineering，Tianjin University，Tianjin 300072，China)

Piston effect has great influence on unsteady airflow in the subway station and tunnel. In this paper，in-situ measurement data and computational fluid dynamics(CFD)method are used to analyze the three-dimensional unsteady air flow in the subway station and tunnel. The experimental analysis of train-induced unsteady flow was conducted in a real station with platform bailout doors(PBD)and air velocity variations with time were recorded. Dynamic mesh method is used for the full-scale model in the unsteady numerical analysis. The results indicate that standard k-ε equation is appropriate for the simulation of the high Reynolds number airflow in tunnel and station as it agrees well with the experimental data. There exist specific diversion and suction ratios in each channel of the airflow for piston wind. And the proportion between bypass duct and platform is stable in either open system or close system. The results of this study can be utilized as basic data for operating tunnel ventilation systems.

standard k-ε equation；draught relief shaft；bypass duct；full-scale model；diversion ratio

TU834

A

0493-2137(2014)02-0168-06

10.11784/tdxbz201207062

2012-07-23；

2012-10-19.

国家“十二五”科技支撑计划资助项目(2011BAJ08B08-2).

由世俊（1955— ），男，教授.

由世俊，yousj@tju.edu.cn.