时域光学拓扑成像方法的模拟和实验研究

高 峰，段临晶，李 娇，张 伟，易 茜，武林会，王 欣

(1.天津大学精密仪器与光电子工程学院，天津 300072；2.天津市生物医学检测技术与仪器重点实验室，天津 300072)

时域光学拓扑成像方法的模拟和实验研究

高 峰1,2，段临晶1，李 娇1,2，张 伟1，易 茜1，武林会1，王 欣1

(1.天津大学精密仪器与光电子工程学院，天津 300072；2.天津市生物医学检测技术与仪器重点实验室，天津 300072)

针对现有的以修正的朗伯-比尔定律(modified Lambert-Beer law，MLBL)为理论模型的光学拓扑方法存在量化度不准确的问题，提出了一种基于最小二乘拟合算法的时域光学拓扑成像方法．该方法利用时域扩散方程在半无限空间条件下的解析解和测量曲线实现最佳匹配以计算相邻的源点与探测点之间的待测组织吸收系数变化值．对该时域光学拓扑成像方法进行了一系列的模拟验证，并以基于时间相关单光子计数(time-correlated single photon counting，TCSPC)技术的多通道时间分辨测量系统为平台进行了实验验证．结果表明：所提出的最小二乘拟合算法总体上优于传统的基于经验值光程的MLBL方法．

扩散方程；飞行时间；时间相关单光子计数；光学拓扑；脑功能成像

近红外光谱成像技术(near-infrared spectroscopy，NIRS)以其安全无损、非电离辐射等优点而在医学成像领域得到广泛关注．选择近红外“治疗窗口”范围内的波长，不仅可以实现对活体组织的无损伤、实时地探测和成像，还可以直接同时提供脑部氧合血红蛋白和还原血红蛋白的浓度变化信息[1]．

由于近红外光在脑部组织穿透深度的限制，一般采用拓扑的方式研究大脑皮层应激反应过程．光学拓扑成像即是利用反射测量给出待测组织体表面下浅层的光学参数二维变化．与其他成像方式相比，光学拓扑成像具有灵活可变的源-探测阵列排布；由于只选择测量与源相邻的探测点处的反射光流，并将其与中间采样点相关联，因而具有较高的信噪比．

近红外光学拓扑成像可采用3种测量模式：连续光、频域和时域[2]．时域模式在信息完整性、数据灵活性、系统稳定性以及随之体现的成像质量稳健性、多参数重建等诸多关键性能上具有其他测量模式不可比拟的综合优势[3]．

针对现有的光学拓扑成像方法理论模型简单、量化误差大等问题，笔者提出了一种利用时域扩散方程在半无限空间条件下的解析解和测量曲线实现最佳匹配以计算相邻的源点与探测点之间的待测组织吸收系数变化值的时域光学拓扑成像方法．本文对该时域光学拓扑成像方法进行了一系列的模拟实验验证，并以基于时间相关单光子计数(time-correlated single photon counting，TCSPC)技术[4]的多通道时间分辨测量系统为平台进行了实验验证．实验结果表明，相较于基于经验值光程的修正的 Lambert-Beer定律(modified Lambert-Beer law，MLBL)方法的量化度过估计和成像区域不均匀现象，时域测量方法对异质体的重建值和重建形状更为理想．该时域光学拓扑成像方法不仅可以灵活设计源-探测器排布阵列，亦可采取多波长测量模式，获取生物组织更多组分信息，因而有望成为现有脑功能成像方法的有益补充．

1 近红外时域光学拓扑成像方法

1.1 基于时域扩散方程解析解的最小二乘拟合算法

对于光在低吸收、高散射组织体的传播行为，扩散方程应用得较为广泛．时域形式的扩散方程表示如下：

反射测量方式下，源和探测器距离较小，相较于大脑轮廓，每对源-探测器下的组织体表面曲率很大，故本文将待测组织体近似为平面半无限空间．在平面半无限空间媒质外推边界条件下，组织体表面距源点ρ处的探测点反射光流量为

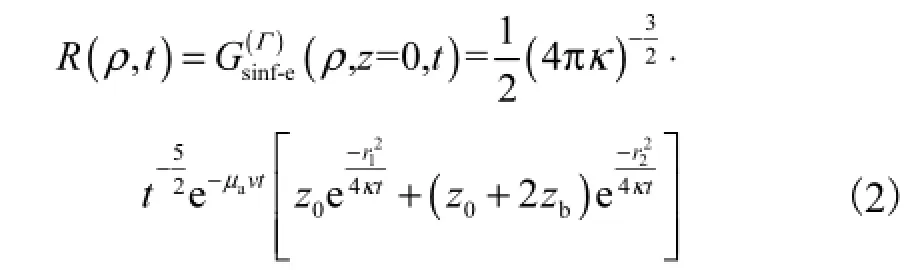
在实际临床应用中，研究者更关心光学参数的相对变化量．在此，本文定义待测组织在光学参数变化前的状态为“rest”，光学参数变化后的状态为“task”.待测组织从 rest状态变化到 task状态期间，约化散射系数改变量远小于吸收系数改变量可忽略不计[5]．结合式(2)，有如下关系式：

实际测量中，一般要考虑仪器响应函数(instrument response function，IRF)的影响，俗称“空测曲线”．对式(3)两边做卷积，有

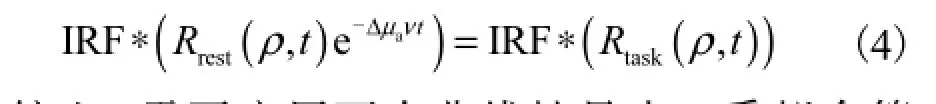
综上，需要应用两次非线性最小二乘拟合算法．对式(4)左边应用一次最小二乘拟合算法可以同时重建待测组织rest状态的吸收系数μa0和散射系数对式(4)右边应用一次最小二乘拟合算法即可获得Δμa．

在后面的验证过程中，基于时域扩散方程解析解的最小二乘法用LSM表示．

1.2 基于计算值光程的修正的Lambert-Beer方法

对于光学厚层媒质，由于多次散射的作用增加了光子在组织体中传输的路径长度，因此，被接受的光信号在介质内部的平均传播距离要大于入射点与接收点之间的几何距离ρ．光子在组织中的运行路程定义为光程，用L表示[6]．MLBL定理可表示为

式中：A为光密度；I0为入射到组织表面的平均光强；I1为探测器在组织表面探测到的平均光强；ε为待测组分的摩尔吸光系数；C为待测组分的浓度；B为路径修正因子；G为与μs相关、与μa无关的强散射衰减．B和G可认为是常数．

当一定光强入射到组织体，设在 rest、task状态下，出射光强分别为Irest和Itask．由MLBL可知，待测组织task状态相对于rest状态的光密度变化为

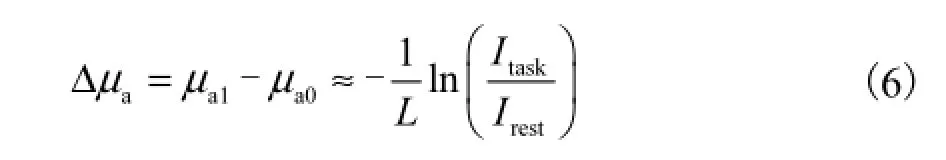
由式(6)可知，时域和连续波模式的差别在于对光程的确定方法不同．时域模式可以利用光子在组织体中的平均飞行时间〈t〉来确定如式(7)所示．连续波测量模式一般取经验值来近似平均光程，如式(8)所示．

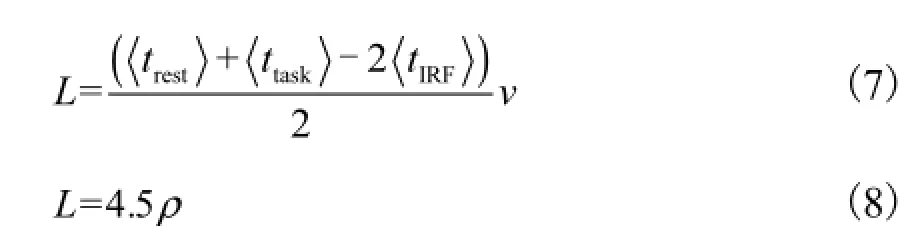
在后面的验证过程中，基于计算值光程的MLBL计算结果用飞行时间的符号＜t＞表示；基于经验值光程的 MLBL计算结果用经验值(empirical value，EV)表示．

2 近红外光学拓扑成像方法模拟验证

本文利用蒙特卡洛(Monte-Carlo，MC)模拟产生正向数据[2]．MC模拟的数值模型为80,mm×80 mm×30,mm 的平板．在图1(a)所示的坐标系下，(-7.5,mm，-3.75,mm)位置处有一深度为20,mm的圆柱形凹槽，直径D分别为 6,mm、7.5,mm、10,mm、14,mm．采用21源-4探测器配置，其中D1、D2、D3、D4为探测点位置，由此形成32个源-探测器对，对应32个直接测量采样点和17个间接采样点，如图1(b)所示．源-探测器最小距离ρ=7.5,mm，成像区域范围为 30,mm×30,mm．数值模型的背景光学参数：吸收系数约化散射系数；异质体光学参数：吸收系数，约化散射系数和背景保持一致．

利用前面提及的 3种方法处理模拟的 MC数据，重建结果如图2和图3所示．

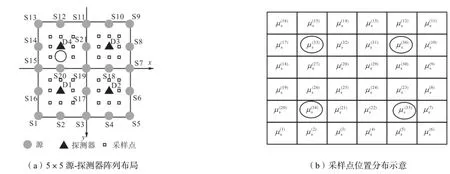
图1 5×5源-探测器阵列Fig.1 5×5,source-detector array

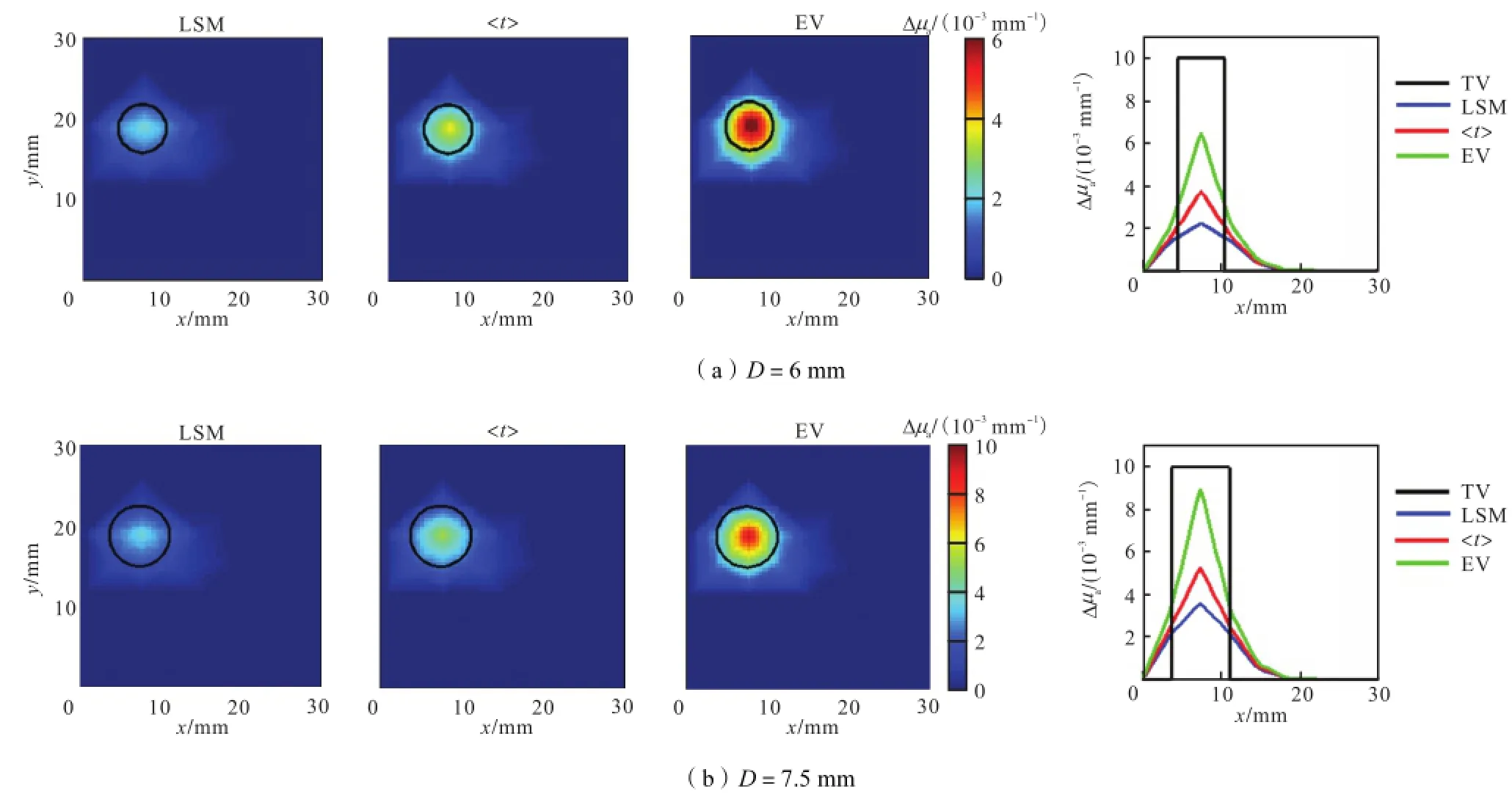
图2 5×5源-探测器阵列模拟重建结果(D=6 mm，7.5 mm)Fig.2 Reconstructed images under a 5×5 source-detector array(D=6 mm，7.5 mm)

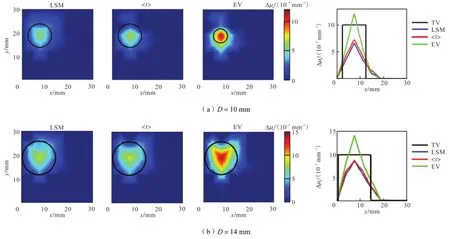
图3 5×5源-探测器阵列模拟重建结果(D=10 mm，14 mm)Fig.3 Reconstructed images under a 5×5 source-detector array(D=10 mm，14 mm)

随着异质体直径 D的增大，每种方法的量化度都会相应提高．在所有情况下，按照量化度从大到小排列，依次是基于经验值光程的MLBL方法、基于计算值光程的 MLBL方法、基于时域扩散方程解析解的最小二乘拟合算法．但当D大于源和探测器距离ρ时，基于经验值光程的 MLBL方法在量化度方面会出现过估计问题，出现偏差．而此时，时域测量方法的计算结果更加理想．

对于目标体的重建结果形状方面，基于经验值光程的 MLBL方法与实际偏差最大，经常会出现异质体中间值估计过高而边缘值估计过低的现象．相对而言，时域测量方法的重建结果中此现象有所改善，其中基于时域扩散方程解析解的最小二乘拟合算法对异质体的形状重建最符合实际．因此，当D超过源和探测器之间的距离ρ时，时域测量方法对异质体的重建值和重建形状更为理想．

3 近红外光学拓扑方法实验验证

3.1 多通道时间分辨测量系统

为了进一步验证提及的两种时域算法的可行性和有效性，本文利用实验室现有的基于 TCSPC的多通道时间分辨测量系统[7]进行了一系列的仿体验证实验．系统原理如图 4所示，包括光源部分、光纤传输部分、探测部分和计算机．

(1)光源部分．为了更好地反映组织体中血红蛋白的浓度变化并有效区分氧合血红蛋白和还原血红蛋白，本系统采用两套发射波长位于近红外波段分别为830,nm和780,nm的皮秒半导体激光器系统(PDL 828Sepia Ⅱ，德国 PicoQuant Inc)作为发射光源．每套激光器系统由激光头和激光器控制模块组成．两套系统激光头(型号分别为 LHD-P-830和 LHD-P-780，德国 PicoQuant Inc)的发射波长分别为 830,nm和780,nm，它们的激光器控制模块相同．激光器的重复频率为 80,MHz，功率可调，峰值功率为 300～400 μW．本系统采用了波分复用器(WDM，加拿大 OZ Optics Ltd)将两路激光信号耦合成一路激光信号．1∶16光开关用于切换源通道，实现了发射光源在 16个不同的入射源点间进行切换．光开关通过FC(ferrule connection)接口与计算机进行连接和通信．用户通过计算机VB界面控制源通路的选择．

(2)光纤传输部分．包括16孔洞光纤架和16根传输光纤．光纤架由钢质材料制成，其表面镀有一层黑色的氧化膜以防止对光线的反射．光纤架用于固定源、探测光纤以实现光源从不同源点入射，探测器从不同的探测点接收反射光．为了减少位于组织体上探头的数目以及精确地获得反射光信息，传输光纤采用同轴光纤结构，即源光纤位于中心，探测光纤位于外环．系统包括 16根源光纤，其中 4根同时用作探测光纤．入射光纤芯径为 62.5 μm/0.22，探测光纤芯径为500 μm/0.37．

(3)探测部分．光子经过组织体的吸收和散射作用，有的被组织体吸收，有的溢出组织体表面．溢出组织体表面的光子被4根探测光纤所接收，经过准直器(F230FC-B，Thorlabs Inc)和调节光强的滤光轮(FW102B，Thorlabs Inc)注入 4个光电倍增管(photomultiplier tube，PMT)，PMT输出的光子脉冲通过TCSPC(SPC-134，德国Becker& Hickl Inc)进行计数，得到出射光子的时间扩展曲线．需要注意的是，由于 PMT为微弱光测量仪器，环境日光强度较大会损坏PMT，故本实验操作环境必须为暗室．

(4)计算机．集成控制各模块工作，进行数据处理和图像重建．

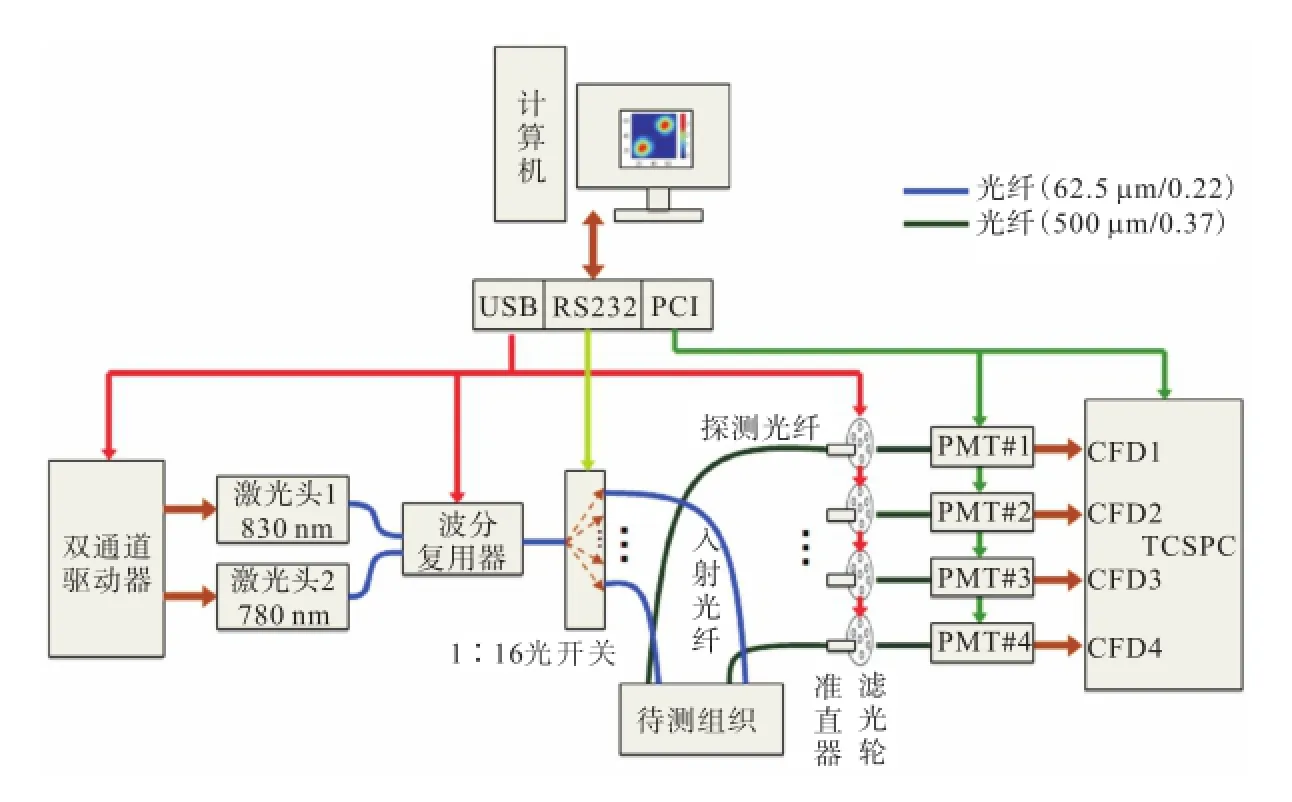
图4 双波长时域光学拓扑成像系统原理Fig.4 Schematic of the dual-wavelength，time domain optical topography system

3.2 仿体验证

本文采用固-液混合仿体，固态模拟均匀背景，液态模拟异质体．仿体是材质为聚甲醛、高H'=50 mm、直径D'=110,mm的圆柱．在圆柱体正中心，有一个深20,mm，直径D分别为10,mm、20,mm的圆柱形凹槽．凹槽的直径和位置代表异质体的大小和位置，如图 5所示．在凹槽中加入按一定比例配制的Intralipid和印度墨水的混合液，其中 Intralipid用来模拟散射介质，印度墨水用来模拟吸收介质[8]．相应实验重建结果如图6～图11所示．

实验结果表明，3种方法的重建结果量化值与前面提到过的模拟结果相似．即按照从大到小排列依次是基于经验值光程的 MLBL方法、基于计算值光程的 MLBL方法、基于时域扩散方程解析解的最小二乘拟合算法．但当异质体的直径D=ρ=10,mm的时候，基于经验值光程的 MLBL方法就已经开始出现过估计问题，即在量化度方面会出现偏差．分析其原因，可能是由于实验测量过程中的基底噪声与其他非线性噪声的影响造成的．而重建结果的形状情况亦与模拟结果相似，即基于经验值光程的 MLBL方法亦会出现异质体中间值估计过高而边缘值估计过低的现象．综上所述，实验结果均与模拟结果相符合，证明了当异质体尺寸 D接近或超过源和探测器之间的距离ρ 时，时域测量方法对异质体的重建值和重建形状更为理想．

图5 实验示意Fig.5 Experimental setup

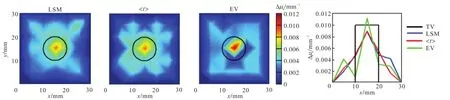
图6 仿体实验结果(D＝10,mm，)Fig.6 Phantom experimental results(D＝10,mm，)

图7 仿体实验结果(D＝10,mm，)Fig.7 Phantom experimental results(D＝10,mm，)

图8 仿体实验结果(D＝10,mm，)Fig.8 Phantom experimental results(D＝10,mm，)

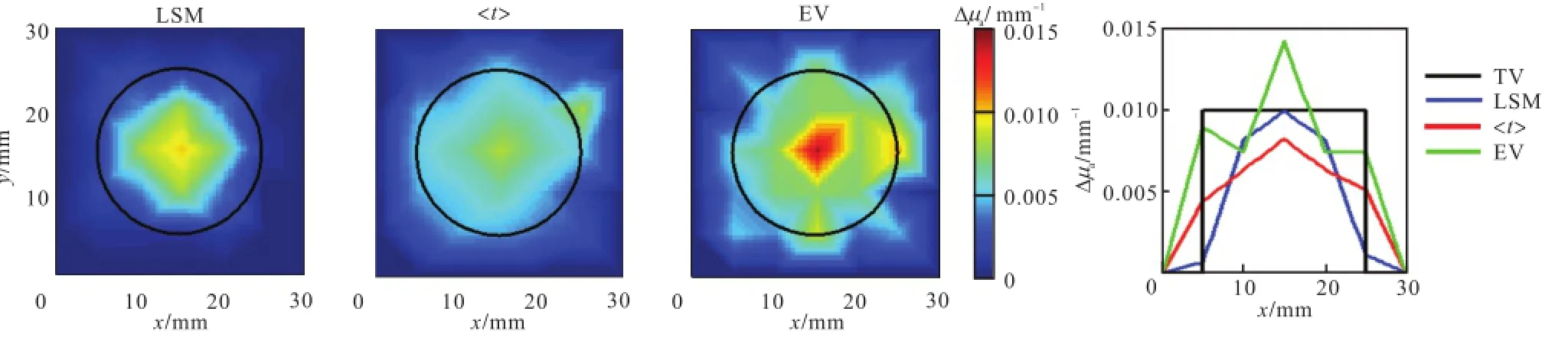
图9 仿体实验结果(D＝20,mm，)Fig.9 Phantom experimental results(D＝20,mm，)

图10 仿体实验结果(D＝20,mm，)Fig.10 Phantom experimental results(D＝20,mm，)

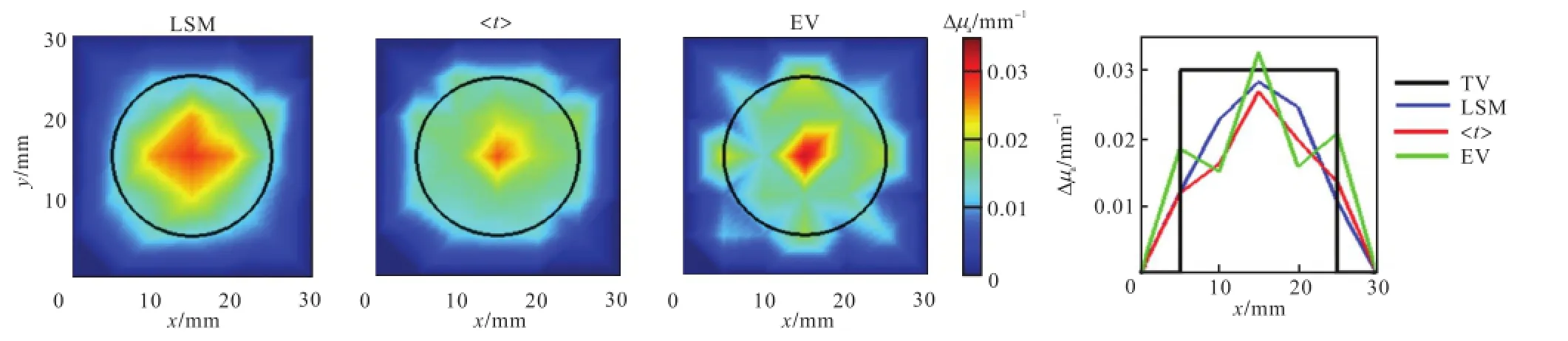
图11 仿体实验结果(D＝20,mm，)Fig.11Phantom experimental results(D＝20,mm，)

4 结 语

本文提出了一种在时域测量数据和时域扩散方程在平面半无限空间条件下的解析解之间寻求最佳匹配的时域光学拓扑成像方法，并进行了一系列的模拟和仿体实验，从而得到待测组织光学参数变化的2D图像．仿体实验在实验室已搭建的基于 TCSPC的多通道时域测量系统平台上进行．模拟和实验结果表明，该方法在量化度上优于传统的基于经验值光程的MLBL方法．

［1］ Zhao Huijuan，Gao Feng. Time-resolved diffuse optical tomographic imaging for the provision of both anatomical and functional information about bio1ogical tissue [J]. Applied Optics，2005，44(10)：1905-1916.

［2］ 徐可欣，高 峰，赵会娟. 生物医学光子学[M]. 北京：科学出版社，2011.

Xu Kexin，Gao Feng，Zhao Huijuan. Biomedical Photonics[M]. Beijing：Science Press，2011(in Chinese).

［3］ Correia T，Lloyd-Fox S，Everdell N，et al. Threedimensional optical topography of brain activity in in fants watching videos of human movement [J]. Physics in Medicine and Biology，2012，57(5)：1135-1146.

［4］ Becker W，屈军乐. 高级时间相关单光子计数技术[M]. 北京：科学出版社，2009.

Becker W，Qu Junle. The Technique About Advanced Time-Correlated Single Photon Counting [M]. Beijing：Science Press，2009(in Chinese).

［5］ Taroni P，Bassi A，Spinelli L，et al. Time-resolved diffuse optical spectroscopy：A differential absorption approach [J]. Appl Spectrosc，2010，64(11)：1220-1226.

［6］ Liebert Adam，Kacprzak Michal，Maniewski Roman. Time-resolved reflectometry and spectroscopy for assessment of brain perfusion and oxygenation[J]. Biocybernetics and Biomedical Engineering，2007，27(2)：237-266.

［7］ Contini D，Torricelli A，Pifferi A，et al. Multichannel time-resolved tissue oximeter for functional imaging of the brain[J]. IEEE Transactions on Instrumentation and Measurement，2006，55(1)：85-90.

［8］ Gao Feng，Zhao Huijuan，Tanikawa Yukari，et al. Optical tomographic mapping of cerebral hemodynamic by means of time-domain detection：Methodology and phantom validation[J]. Physics in Medicine and Biology，2004，49(6)：1055-1078.

（责任编辑：赵艳静）

Simulation and Experimental Investigation on Time Domain Optical Topography

Gao Feng1,2，Duan Linjing1，Li Jiao1,2，Zhang Wei1，Yi Xi1，Wu Linhui1，Wang Xin1
(1. School of Precision Instrument and Opto-Electronics Engineering，Tianjin University，Tianjin 300072，China；2. Tianjin Key Laboratory of Biomedical Detecting Techniques and Instruments，Tianjin 300072，China)

To cope with the low quantification in the established optical topography that originates from the excessively simplified computation model based on the modified Lambert-Beer’s Law(MLBL)，we proposed a leastsquares fitting scheme for time domain optical topography that seeks data matching between the time-resolved measurement and model prediction calculated by analytically solving the time-domain diffusion equation in semi-infinite geometry. A series of experiments were also conducted，including simulation and phantom verification．The phantom verification was performed with multi-channel time-resolved measurement system based on TCSPC．Our simulative and phantom experiments demonstrate that the proposed curve-fitting method is on the whole，superior to the conventional MLBL-based one in quantitative performance.

diffusion equation；flight time；time-correlated single photon counting；optical topology；functional cerebral imaging

Q63

：A

：0493-2137(2014)09-0829-07

10.11784/tdxbz201305068

2013-05-21；

2013-09-24.

国家高技术研究发展计划(863计划)资助项目(2009AA02Z413)；国家自然科学基金资助项目(81271618)；教育部高等学校博士学科点专项科研基金资助项目(20120032110056).

高 峰（1963— ），男，教授.

高 峰，gaofeng@tju.edu.cn.

时间：2013-11-18.

http://www.cnki.net/kcms/detail/12.1127.N.20131118.1627.001.html.