疏排桩-放坡组合支护的应用分析

张锡治，何明华

(1.天津大学建筑设计研究院，天津 300072；2.天津大学建筑工程学院，天津 300072)

疏排桩-放坡组合支护的应用分析

张锡治1，何明华2

(1.天津大学建筑设计研究院，天津 300072；2.天津大学建筑工程学院，天津 300072)

针对某基坑放坡开挖不满足稳定性要求的问题，提出采用疏排桩与放坡组合支护的方案．通过有限元强度折减法，分析了疏排桩加设前后的土坡稳定性及疏排桩的位置、桩径、桩距、桩长对土坡稳定性的影响．在给定的目标下统一考虑各因素的影响，根据经济性比较得出优化方案．分析表明有限元强度折减法分析非均质土坡稳定可行，加设疏排桩能加深滑裂面、提高土坡稳定性. 工程应用表明疏排桩与放坡组合支护的方案是经济有效的支护方式.

疏排桩；土坡稳定；强度折减法；有限元分析；方案优化

在基坑支护中，放坡开挖是简单经济的一种方式，它适用于地基土质较好、开挖深度不大、地下水位较低及施工现场有足够放坡场所的工程．对于有些条件不满足而希望放坡开挖的工程，可经分析后采取适当措施提高开挖土坡的稳定性．天津开发区某基坑深度较浅，土质较差，地下水位较高，尝试采用疏排桩与放坡组合的方案．

疏排桩-放坡组合支护的关键问题是保证开挖土坡的稳定性．土坡的稳定性问题是土力学中的经典问题，建立在传统极限平衡理论基础上的稳定分析方法往往需要假设滑裂面形状，不考虑土体本构关系，无法反映出边坡破坏的发生和发展过程[1-2]．随着计算机技术的发展，有限元强度折减法得到了很好的发展．此方法不需要假定边坡破坏面，可以直接求出安全系数，能很好地分析复杂边坡并能模拟桩与土的相互作用．该方法最早是由 Zienkiewicz等[3]提出，后来，Griffiths和Lane[4]、Dawson等[5]、Cheng等[6]学者利用该法分析了土坡稳定性．近年来，国内外学者也利用该法对抗滑桩加固的边坡进行了深入的研究. Cai等[7]研究了单排抗滑桩桩距、桩头约束、抗弯刚度、桩的位置对加固边坡整体安全系数的影响．Won等[8]对相同土坡利用极限平衡法和有限差分软件FLAC3D分析了边坡-抗滑桩系统的稳定性. Wei和Cheng[9]研究了边坡单排桩的临界滑动面和桩的最佳位置．韦立德等[10]进行了抗滑桩优化探讨．年廷凯等[11]分析了均质土坡下桩间距与桩径比、合理桩长、合理设桩位置等．陈乐求等[12]通过编制程序分析了抗滑桩的桩长和桩的位置对土坡稳定性的影响．以上研究都是针对无超载且土质较好的均质土坡，本文利用 ABAQUS有限元软件，采用强度折减法，对开挖形成的土坡进行稳定性分析，并考虑桩土相互作用，对疏排桩-放坡组合支护方案的可行性与设桩方案的优化进行有限元分析．

1 计算原理

1.1 强度折减法概念

强度折减法[1-3]是在计算中假定外荷载不变，利用式(1)和式(2)调整土体的强度指标黏聚力c、内摩擦角ϕ，然后对土坡进行有限元分析．通过不断地增加折减系数，反复分析土坡，直至其达到临界破坏，此时得到的折减系数即为安全系数Fs．

式中Ft为折减系数．

1.2 土体和疏排桩的本构模型

土体和疏排桩采用实体单元模拟，疏排桩被视为理想线弹性体，土体采用服从Mohr-Coulomb破坏准则与非关联流动法则的理想弹塑性本构模型．在ABAQUS程序中，其破坏面在子午面(Rmcq-p)上定义[13]为

ABAQUS中的 Mohr-Coulomb模型采用连续光滑的塑性势面 G，其在子午面上为双曲线函数，在偏平面为光滑的椭圆函数，故其塑性流动在偏平面上总是非关联的．其塑性势函数定义为

其中

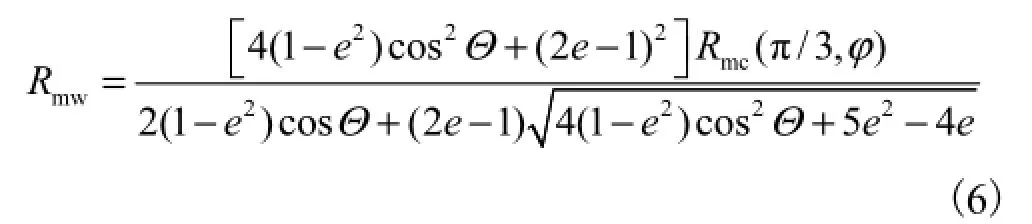
式中：ψ为剪胀角；0|c为初始黏聚力，即没有塑性变形时的黏聚力；ε为子午面上的偏心率，它控制着塑性势面 G的形状及接近于其渐进线的速度，通常取0.1；e为π面上的偏心率，它控制着塑性势面G在偏平面的扁平程度，其范围为1/2 1e≤ ≤ ，一般取

1.3 桩土接触面模型

在 ABAQUS软件中，可采用主从接触对算法模拟桩与土间接触面之间的相互作用[13-14]，接触面之间的相互作用包含接触面的法向作用和接触面的切向作用．接触面的法向模型采用硬接触，即桩土只有在压紧状态时才能传递法向应力，若桩土之间有间隙时则不传递法向压力．接触面的切向模型采用Coulomb摩擦模型描述接触面的摩擦特性．如图 1所示，用摩擦系数 μ表征接触面间的摩擦行为．如果两表面间的接触压力为p，则接触面间的摩擦力的极限值为 pμ ，当接触面上的剪应力达到该极限值时，接触面上发生相对滑动．在理想状况下，接触面在滑移状态之前是没有剪切变形的，但这会造成数值计算上的困难．为避免数值计算困难，ABAQUS引入“弹性滑移变形”的概念，在黏结的接触面之间允许发生少量的相对滑移变形．

图1 界面摩擦特性Fig.1 Friction behavior of interface

2 工程概况

本工程位于天津滨海新区，拟建物为1栋5层机房，占地面积 4,040.7,m2，建筑面积 23,360,m2，整场地分布单层地下车库，采用桩基础．基坑深 3.8,m，基坑等级为3级，基坑平面示意见图 2，关键部位设有6个位移监测点．该场地为软土地基，土层参数见表1．表层地下水属潜水类型，年变幅在 0.50～1.00,m左右，设计中地下水埋深按1.0,m考虑．

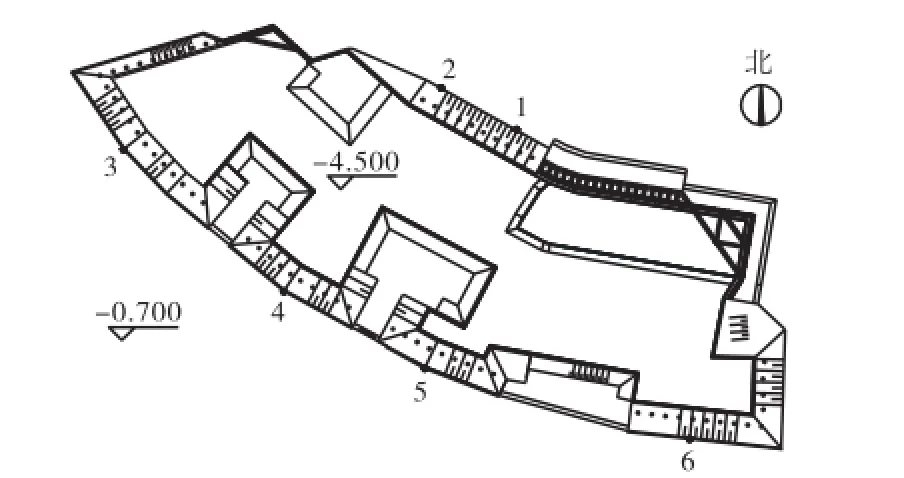
图2 基坑平面及监测点布置示意Fig.2 Foundation pit plan and observation point arrangement

经分析直接放坡开挖，土坡稳定性不满足规范要求但指标与规范要求相差不超过20%，因而考虑采用疏排桩与放坡开挖组合的方案，基坑东北角因场地所限不具备放坡条件而采用密排桩支护．

表1 土体参数Tab.1 Soil parameters

3 模型介绍

基坑边坡剖面如图 3所示，坡高 3.8,m，坡高比1∶1.5，地基计算深度 22,m．边界条件为：下部固定约束，上部自由边界，前后左右为水平方向约束．坡顶地面超载取为10,kPa．

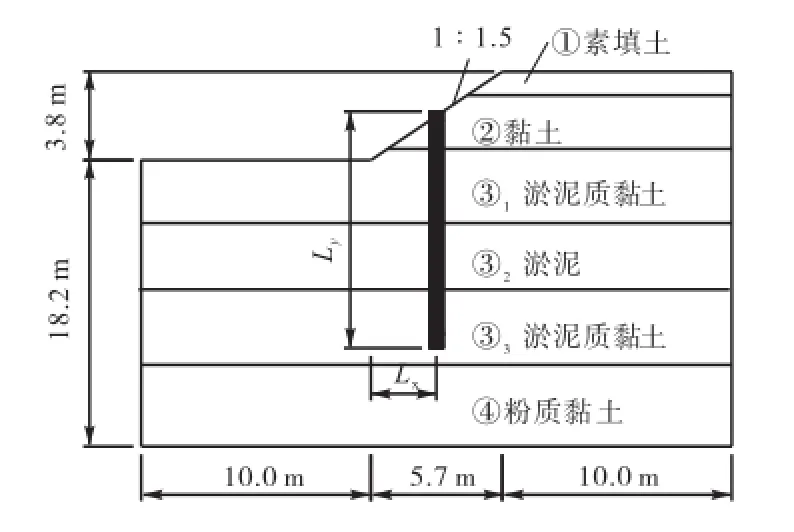
图3 土坡的剖面图Fig.3 Slope profile

有限元模型如图4所示，疏排桩被视为理想线弹性体，弹性模量和泊松比分别为 30,000,MPa和0.20．土体采用服从 Mohr-Coulomb破坏准则与非关联流动法则的理想弹塑性本构模型．各层土的弹性模量和泊松比如表 1所示，桩土摩擦系数按μ=tan(0.75ϕ)取值如下：①、②、③1土层摩擦系数为0.112；③2、③3、④土层摩擦系数分别为 0.084、0.145、0.214．

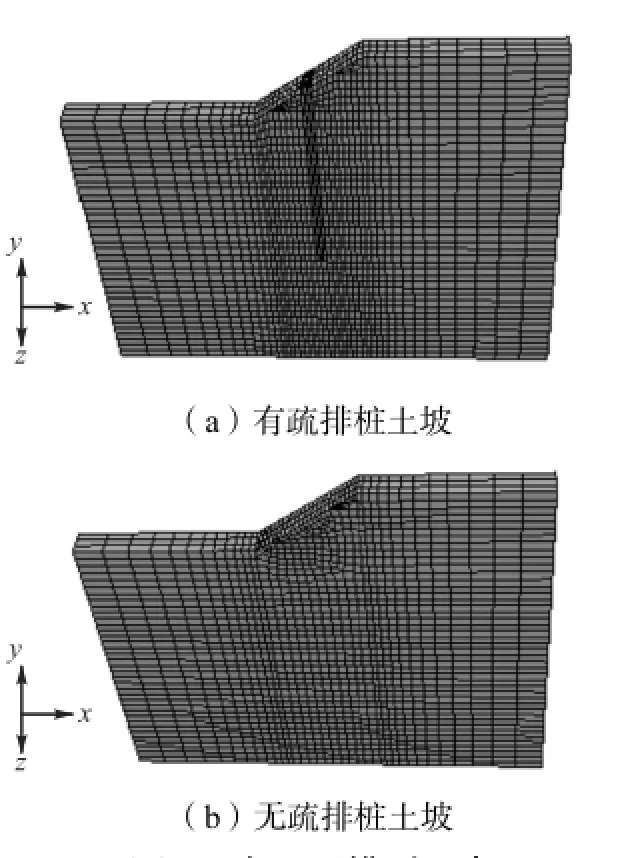
图4 有限元模型示意Fig.4 FEM model

4 计算与分析

4.1 临界破坏标准的选择

目前，临界破坏评价标准主要有以下3种[15]：①特征点处的位移突变；②广义塑性应变或者等效塑性应变从坡底贯通到坡顶；③有限元计算不收敛．下面对无疏排桩土坡的稳定安全系数，采用3种临界破坏准则进行有限元计算，并与极限平衡法的结果比较．

从表2可知，按3种临界破坏准则得到的有限元计算结果接近．与极限平衡法的结果比较，有限元计算结果与按简化毕肖普和简布法得出的结果接近，与按瑞典条分法得出的结果相差较大，这是由于瑞典条分法未考虑土条间的力，偏于安全．综合比较，采用有限元强度折减技术计算非均质土坡稳定安全系数是可行的．考虑结果判断的方便，以数值不收敛为临界破坏准则．

表2 土坡稳定安全系数Tab.2 Safety factor of slope

4.2 加设疏排桩后土坡稳定分析

初始考虑将桩设置在拟开挖土坡中部，采用桩径0.6,m、桩间距 3,m、桩端锚入③3淤泥质黏土、桩长采用12,m．建立有疏排桩土坡有限元模型，土体划分的网格与无桩时尽量一致，桩土之间接触面附近的网格细划，进行如下比较．

4.2.1 稳定安全系数

图 5所示为有无疏排桩土坡的坡顶水平位移与强度折减系数的关系曲线．根据计算不收敛可得加疏排桩土坡稳定安全系数 Fs=1.258，与无疏排桩的不收敛点 Fs=1.154比较，土坡稳定安全系数提高了0.104．

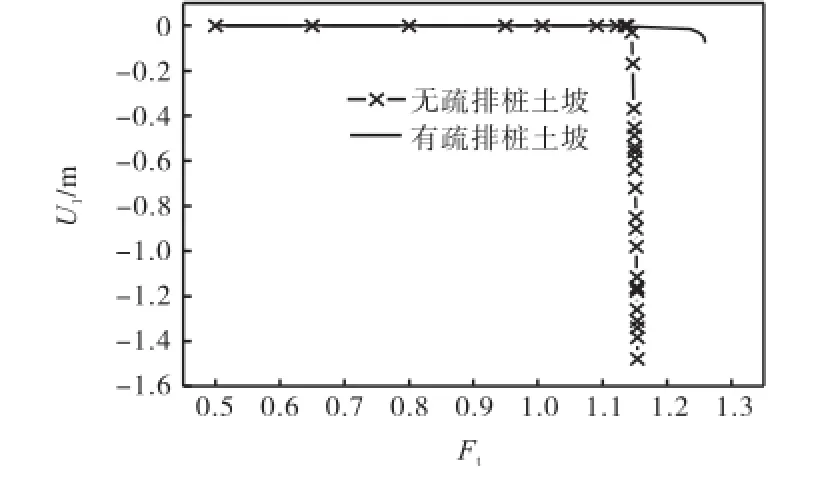
图5 土坡顶点水平位移U1与强度折减系数Ft的关系Fig.5 Relationship between horizontal displacement u1of slope top and shear strength reduction factor Ft

4.2.2 滑动面

图 6为有无疏排桩计算终止时的增量位移等值线云图，从两图对比可发现，加疏排桩后土坡产生位移的区域明显比无桩时的范围要大，加疏排桩后土坡滑动面向更深土层发展，这主要是由于桩将土体下滑产生的内力传向了更深土层．

4.3 疏排桩设计方案优化

对于给定的土坡，疏排桩加固土坡效果的影响因素主要有疏排桩的设置位置、桩径、桩间距和桩长．下面分析该工程中疏排桩的位置、间距、桩长和桩径对土坡稳定性的影响，在提高土坡稳定安全系数0.2的目标下，综合考虑各种影响因素，根据经济性比较得出优化方案．

图6 增量位移等值线云图Fig.6 Nephogram of displacement increment

4.3.1 桩位置的影响

为确定桩的最佳位置，对不同桩长、桩距、桩径在不同位置上分别进行了三维有限元计算，得到相应的土坡稳定安全系数，见图7．桩的位置Lx/Lh分别为-0.053、0.184、0.4、0.5、0.6、0.8、1.053、1.2，其中 Lx为距坡脚的距离，朝坡顶方向为正；Lh为斜坡的水平距离，Lh=5.7,m(见图3)．桩长L为12,m和17,m，桩距S为3.0,m和4.5,m，桩径D为0.6,m和0.8,m．

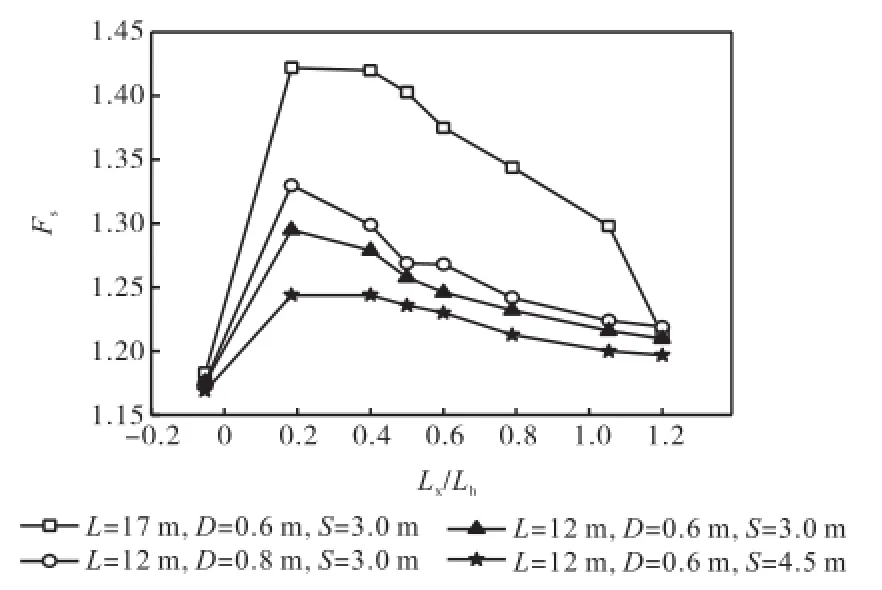
图7 桩的位置对土坡稳定性的影响Fig.7 Effect of pile location on slope stability

从图 7的计算结果可知，不同的间距、桩长、桩径，最佳设桩位置基本一致．与无超载的均质土坡不同，该开挖土坡中，桩在 Lx/Lh=0.184～0.400之间效果较好．在斜坡上加大桩长，能明显提高土坡稳定性，而在坡顶和坡脚处加大桩长，土坡稳定性提高很小．

4.3.2 桩长与桩距的影响

在该土坡的最佳设桩位置，即 Lx/Lh=0.184，在桩径 D分别为 0.6,m和 0.8,m时，取桩长分别为10,m、12,m、13,m、14,m、15,m、16,m、17,m、18,m，桩距 S为 2.5,m、3.0,m、3.5,m、4.0,m、4.5,m，计算得到如图8所示的关系曲线．

计算结果表明不同桩径下的桩长与桩距对土坡稳定性的影响规律基本一致，土坡稳定安全系数随桩距增大而逐步减小，随着桩长增加逐步提高并趋于稳定．稳定系数在桩长为12,m以下时，提高较缓慢，桩长 12～14,m 之间稳定系数增加较快，曲线斜率增大，而在14～18,m之间，稳定系数的变化很小．这是由于桩长在 10～12,m时，桩底端土层主要为淤泥，桩土摩擦系数较小，桩土相互作用较弱，锚固较差；在 12～14,m处的土层为淤泥质黏土，桩土摩擦系数提高，桩土相互作用增大，锚固增强，曲线的斜率增大，意味着稳定系数提高加快；在14～18,m时，尽管桩土摩擦系数更大，但此时增大锚固效果对土坡稳定影响已经很小了．

图8 桩长和桩距对土坡稳定的影响Fig.8 Effect of pile length and spacing on slope stability

4.3.3 方案经济性比较

为满足土坡稳定性提高 0.2所要求的设置桩方案，同一曲线上取最靠近 Fs=1.354直线的点，同一桩长取最靠近 Fs=1.354直线的点，则满足条件的方案如表3所示，从计算得到的单位纵向长度需要的桩混凝土用量来看，桩径 0.8,m均比桩径 0.6,m 的要大，表明采用大桩径来提高土坡稳定安全系数不经济.

经过经济性对比，采用桩径 0.6,m，桩长 14,m，桩距 4.0,m．这与初始桩径 0.6,m、桩长 12,m、桩距3.0,m，设置在坡面中线上相比既提高了土坡稳定性，又节省了材料．

表3 单位纵向长度的桩混凝土用量Tab.3 Pile concrete volume per longitude length

5 工程应用

本基坑工程采用优化方案，于2012年5月17日进行钻孔灌注桩施工．从2012年7月初开始基坑开挖至2012年9月中旬基础工程施工结束．基坑开挖过程中，进行坑内井点降水，保证地下水低于开挖面0.5,m．基坑开挖期间，监测单位对土坡坡顶的水平位移进行了监测，监测点最终累计水平位移为 11～29,mm，未超过《建筑基坑工程监测技术规范GB50497—2009》规定的预警值，其中 1～6是指图2中的6个位移监测点．图9所示为开挖到一定深度后的坡顶水平位移情况．由图 9可知，在开挖深度3.3,m之前，监测的位移变化缓慢且略小于 FEM 计算的结果；开挖深度达到 3.8,m时，实测位移大于计算结果．这是由于 FEM未考虑土体变形随时间变化引起的差别．

图9 坡顶水平位移与开挖深度的关系Fig.9 Relationship between horizontal displacement of slope top and excavation depth

6 结 论

(1) 通过工程实例，利用 ABAQUS有限元软件对不含疏排桩的非均质土坡进行了三维分析，并与极限平衡法的结果对比，表明有限元强度折减技术计算非均质土坡是可行的．

(2) 非均质土坡的三维有限元分析结果表明，增设疏排桩后，滑动面向深处发展，土坡稳定性提高．

(3) 通过对桩的位置、桩径、桩距、桩长的优化分析，本土坡最佳设桩位置在坡面中下部 1/5处、桩长14,m、桩径0.6,m、桩距4.0,m．

(4) 从工程应用的情况来看，疏排桩-放坡组合支护的方案，是经济有效的基坑支护形式．

［1］ 赵尚毅，郑颖人，时卫民，等. 用有限元强度折减法求边坡稳定安全系数[J]. 岩土工程学报，2002，24(3)：343 -346.

Zhao Shangyi，Zheng Yingren，Shi Weimin，et al. Analysis on safety factor of slope by strength reduction FEM[J]. Chinese Journal of Geotechnical Engineering，2002，24(3)：343-346(in Chinese).

［2］ 栾茂田，武亚军，年延凯. 强度折减有限元法中边坡失稳的塑性区判据及其应用[J]. 防灾减灾工程学报，2003，23(3)：1-8.

Luan Maotian，Wu Yajun，Nian Tingkai. A criterion for evaluating slope stability based on development of plastic zone by shear strength reduction FEM[J]. Journal of Disaster Prevention and Mitigation Engineering，2003，23(3)：1-8(in Chinese).

［3］ Zienkiewicz O C，Humpheson C，Lewis R W. Associated and non-associated visco-plasticity and plasticity in soil mechanics [J]. Geotechnique，1975，25(4)：671-689.

［4］ Griffiths D V，Lane P A. Slope stability analysis by finite elements[J]. Geotechnique，1999，49(3)：387-403.

［5］ Dawson E M，Roth W H，Drescher A. Slope stability by strength reduction[J]. Geotechnique， 1999，49(6)：835-840.

［6］ Cheng Y M，Lansivaara T，Wei W B. Two-dimensional slope stability analysis by limit equilibrium and strength reduction methods [J]. Computers and Geotechnics， 2007，34(3)：137-150.

［7］ Cai F，Ugai K. Numerical analysis of the stability of a slope reinforced with piles[J]. Soils and Foundations，2000，40(1)：73-84.

［8］ Won J，You K，Jeong S，et al. Coupled effects in stability analysis of pile-slope systems[J]. Computers and Geotechnics，2005，32(4)：304-315.

［9］ Wei W B，Cheng Y M. Strength reduction analysis for slope reinforced with one row of piles[J]. Computers and Geotechnics，2009，36(7)：1176-1185.

［10］ 韦立德，杨春和，高长胜. 基于三维强度折减有限元的抗滑桩优化探讨[J]. 岩土工程学报，2005，27(11)：1350-1352.

Wei Lide，Yang Chunhe，Gao Changsheng. Optimization of slide-resistant piles based on strength reduction method with 3D FEM[J]. Chinese Journal of Geotechnical Engineering，2005，27(11)：1350-1352(in Chinese).

［11］ 年廷凯，徐海洋，刘红帅. 抗滑桩加固边坡三维数值分析中的几个问题[J]. 岩土力学，2012，33(8)：2521-2527.

Nian Tingkai，Xu Haiyang，Liu Hongshuai. Several issues in three-dimensional numerical analysis of slopes reinforced with anti-slide piles[J]. Rock and Soil Mechanics，2012，33(8)：2521-2527(in Chinese).

［12］ 陈乐求，杨恒山，林 杭. 抗滑桩加固边坡稳定性及影响因素的有限元分析[J]. 中南大学学报：自然科学版，2011，42(2)：490-494.

Chen Leqiu，Yang Hengshan，Lin Hang. Finite element analysis for slope stability and its influencing factors with pile reinforcement[J]. Journal of Central South University：Science and Technology，2011，42(2)：490-494 (in Chinese).

［13］ Hibbit，Karlsson and Sorensen Inc. ABAQUS/ Scripting Manual(Version 6.8)[M]. Providence：HKS Inc，2008.

［14］ 王金昌，陈页开. ABAQUS 在土木工程中的应用[M].浙江：浙江大学出版社，2006.

Wang Jinchang，Chen Yekai. Application of ABAQUS in Civil Engineering[M]. Zhejiang：Zhejiang University Press，2006(in Chinese).

［15］ 费 康，张建伟. ABAQUS在岩土工程中的应用[M].北京：中国水利水电出版社，2010.

Fei Kang，Zhang Jianwei. Application of ABAQUS in Geotechnical Engineering[M]. Beijing：China Water Power Press，2010(in Chinese).

(责任编辑：樊素英)

Application Analysis of Composite Supporting of Scattered Piles and Step-Slope

Zhang Xizhi1，He Minghua2
(1. Architectural Design and Research Institute of Tianjin University，Tianjin 300072，China；2. School of Civil Engineering，Tianjin University，Tianjin 300072，China)

A composite supporting of scattered piles and step-slope was proposed to deal with the problem that the slope stability of a step-slope excavation engineering cannot meet the requirement. Numerical analyses were performed on the stability of reinforced and unreinforced slope by the finite element strength reduction method. The influence of scattered pile's location，diameter，space and length on slope stability was also analysed，and accordingly an optimal scheme was obtained considering all influencing factors under a given target. Analyses show that the finite element method is feasible in analyzing non-homogeneous slope stability is available and that the application of scattered pile can deepen the slip surface and increase the safety factor of slope. The application of optimal scheme in the engineering indicates that the composite supporting of scattered piles and step-slope is an economical and effective supporting method.

scattered pile；slope stability；strength reduction method；finite element analysis；schema optimization

TU457

：A

：0493-2137(2014)09-0817-06

10.11784/tdxbz201303039

2013-03-19；

2013-08-16.

张锡治（1968— ），男，博士，研究员，zxz@eyou.com.

何明华，minghuatj@126.com.