磨料流体抛光流场分析与实验研究

闫如忠，甘敏华，刘振通

（东华大学 机械工程学院，上海 201620）

磨料流体抛光流场分析与实验研究

闫如忠，甘敏华，刘振通

（东华大学 机械工程学院，上海 201620）

基于流体动压理论和κ-ε湍流模型，利用Fluent仿真研究工艺参数对光学玻璃磨料流体抛光效果的影响趋势.结果表明：流场压力与流体入射速度成正比，与最小加工间隙成反比；流场压力沿限控轮旋转方向逐渐增大，在最小加工间隙之前处达到最大值；流体入射角度为45°时，流场压力达到最大值.依据κ-ε湍流理论和Navier-Stokes方程建立的压力理论模型与仿真计算结果吻合.对K9玻璃进行磨料流体抛光实验研究，结果表明增大流体入射速度能有效地提高玻璃表面质量.

磨料流体抛光；湍流模型；Fluent仿真；流场压力

随着科技的发展，超精密光学玻璃元件在航空航天、天文探索、核能工业和光刻工艺等领域得到广泛应用.光学玻璃要求低表面波纹度、极少的表面瑕疵、完整的晶格结构和极小的残余应力.光学玻璃材料脆性高，断裂韧性低，一般需经过固结磨料加工、离散粒子抛光、纳米级磨料修整3道工序获得高精度光洁表面.离散粒子抛光作为最终或次终工序，目的是消除前道工序的表面残余应力，最终获得平面度亚微米级、表面粗糙度纳米级的优质玻璃表面.离散粒子抛光的主要方法有气囊抛光［1］、磁流变抛光［2］、磨料流体抛光［3］和弹性发射加工［4］等.

磨料流体抛光是一种结合磨料射流理论和弹性发射加工理论的非接触式离散粒子加工方法.本文以磨料流体抛光为研究对象，重点对抛光中的动态参数进行研究，结合流体动压理论，深入分析流体入射速度、喷射角度及最小加工间隙对工件抛光的影响，为磨料流体抛光实验提供依据.

1 磨料流体抛光模型

1.1 磨料流体抛光原理

磨料流体抛光原理如图1所示.高速磨料流体经喷嘴充入旋转的限控轮与光学玻璃表面间的空隙中，利用限控轮限制磨料流体飞溅、约束磨料流体形态，在限控轮的离心力驱动及局部流场压力作用下，形成高能速度场.高能速度场中，磨料颗粒不断地与限控轮及光学玻璃表面发生弹性碰撞，在狭小空间内形成高频振荡，使磨粒可以多次多向冲击工件表面，获得光滑表面.

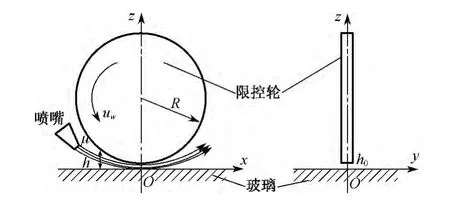
图1 光学玻璃磨料流体抛光原理图Fig.1 Abrasive fluid polishing schematic diagram of optical glass

1.2 磨料流体抛光理论基础

磨料流体抛光的数学描述是基于Preston方程［5］，即工件表面材料去除量Δz与流场压力p成正比的关系，如式（1）所示.

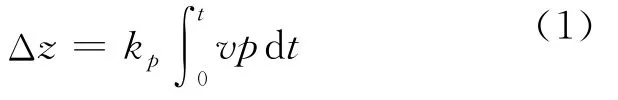
式中：v为磨粒在工件表面的相对速度；t为加工时间；k p是一个包含了诸多影响因素的比例常数，包括流体入射速度、喷射角度、磨粒规格、工件规格等.根据 Navier-Stokes方程［6］及流体动压理论［7］，加工区流场压力与流体入射速度、喷射角度及加工间隙呈线性关系.因此，光学玻璃磨料流体抛光的工艺研究重点是流体入射速度、喷射角度及最小加工间隙.

2 磨料流体抛光流场数学模型

2.1 抛光区域流场建模

为了研究限控轮与玻璃抛光区域流场，作以下简化和假设：限控轮表面为光滑表面；流体为不可压缩的牛顿流体；流体动压力沿膜厚度方向保持不变；加工间隙中心流体的流动为层流，且不计其流动中的惯性效应.根据图1的直角坐标系和Naveir-Stokes方程，可得到限控轮与玻璃抛光区域的数学模型［6-8］为

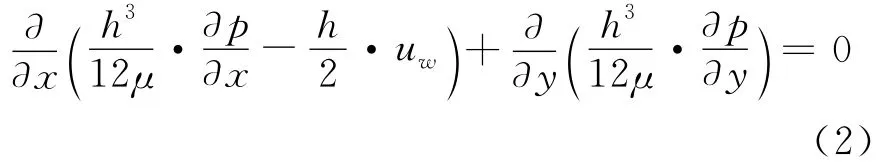
式中：μ为流体动力黏性系数；uw为限控轮线速度；h为加工间隙，h＝h0＋x2／（2R），R为限控轮的半径，h0为最小加工间隙（即x＝0处）.

由Reynolds方程［9］可知抛光区流场压力表示为

由于式（3）是一个二阶偏微分方程，很难用数学方法来解析.本文借助有限元实现κ-ε模型理论（κ为湍动能，ε为湍流耗散率），通过该模型的传输方程求解流场压力分布.

2.2 数值模拟过程中的控制方程组

流体抛光区域射流的实际流动为湍流，本文在进行流场计算时采用标准κ-ε湍流模型，该模型稳定、简单，并在较大的工程范围内具有足够的精度.上述抛光区域内流体流动的方程如下所述.

连续性方程

动量方程

式中：ρ为流体密度；ui和uj为流体的速度分量，i＝1，2，3；j＝1，2，3；xi和xj为直角坐标系；ρFi为质量力.

标准κ-ε方程

κ-ε模型中经验常数的取值通常为C1ε＝1.44，C2ε＝1.92，Cμ＝0.99，κ与ε的湍流普朗特数［10］分别为湍动能σκ＝1.0，σε＝1.3.

3 数值模拟计算

光学玻璃磨料流体抛光过程中，玻璃表面不断受到细微磨粒的冲击而得以微量去除，进而改变玻璃表面质量.由Preston方程可知，加工区域流场压力p是影响材料去除量的一个重要参数，其大小的变化或不稳定性直接影响材料去除率和最终平面度及表面粗糙度.设定抛光区域周围流场为稳态流场，仿真参数如下：流体入射速度u＝30 m／s，喷射角度α＝45°，最小加工间隙h0＝1 mm，限控轮转动速度ω＝175 rad／s，喷嘴直径D＝4 mm，流体动力黏性系数μ＝0.001 Pa·s.

数值计算收敛后其流场压力分布如图2所示.由图2（b）可以看出，抛光区域流场压力大致呈正弦曲线分布，即沿着限控轮旋转方向，流场压力逐渐增大，在即将到达最小加工间隙h0处达到最大值，且越靠近最小间隙处，压力变化梯度越大，在出口区，压力减小，且出现负压，这与式（4）所求得的解析值相一致.

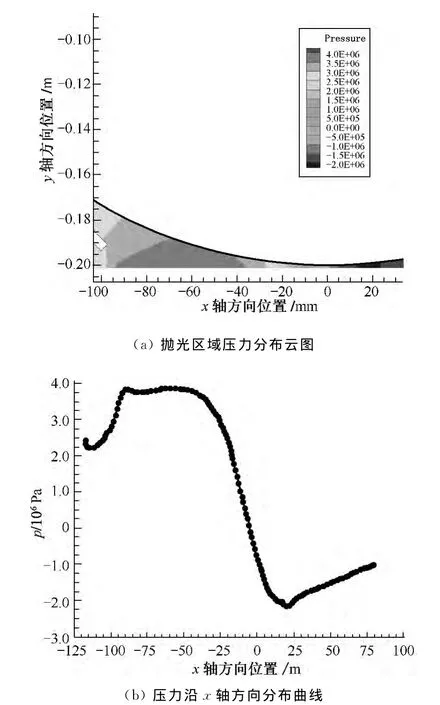
图2 抛光区域流场压力分布图Fig.2 The hydrodynamic pressure distribution of polishing zone

3.1 流体入射速度u对流场压力的影响

在其他仿真参数不变的情况下，设置流体入射速度u分别为10，20，30，40，50，60 m／s，研究流体入射速度u对流场压力的影响，仿真结果如图3（a）所示.由图3（a）可以看出，在一定范围内，流场压力随流体入射速度的增加而增大，这是由于入射速度的增加使流体的剪切力增大，对工件表面产生更大的去除作用，这符合流体动压理论的描述.

3.2 喷射角度α对流场压力的影响

喷射角度定义为射流束与工件表面的夹角.在其他仿真参数不变的情况下，设置流体喷射角度α分别为30°，35°，40°，45°，50°，55°，研究α对流场压力的影响，仿真结果如图3（b）所示.仿真结果表明，喷射角度在30°～45°时，喷射角度越大，抛光区域流场压力越大；但是喷射角度在45°～55°时，喷射角度与流场压力呈反比.流体抛光中，当喷射角度在一定范围内增大时，流体入射速度的水平分量增加，致使流场压力增大.

3.3 最小加工间隙h0对流场压力的影响

在其他仿真参数不变的情况下，设置最小加工间隙h0分别为0.2，0.4，0.6，0.8，1.0，1.2 mm，研究h0对流场压力的影响，仿真结果如图3（c）所示.由图3（c）可以看出，最小加工间隙越小，流场压力越大.在最小加工间隙为0.2～1.2 mm，流场压力与最小加工间隙呈线性关系.仿真结果与式（3）的描述相一致.

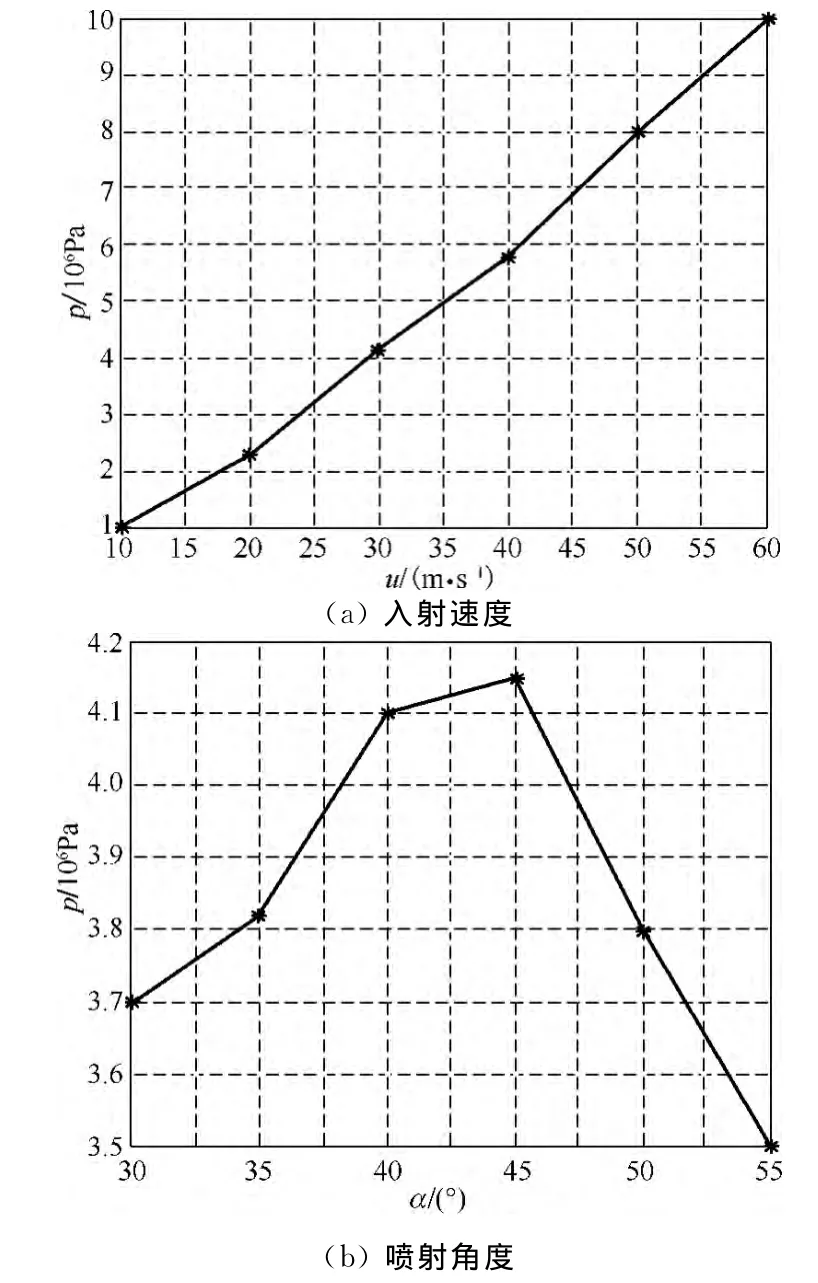
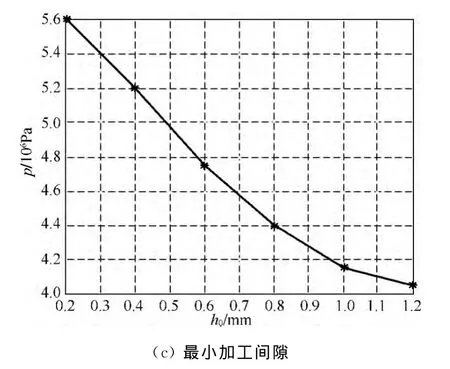
图3 各工艺参数与流场压力之间的关系图Fig.3 Effects of process parameters on the hydrodynamic pressure

3.4 工艺参数影响分析

根据3.1～3.3节分析可知：流体入射速度越大，抛光区域流场压力越大，工件表面可以获得更大材料去除率，但这与抛光设备的流体输出系统直接相关；喷射角度为45°时，流场压力最大；流场压力与最小加工间隙呈反比，抛光实验中可以调节工件与限控轮的最小加工间隙至最小值以获得最佳加工效果.由图3可知，各工艺参数对流场压力的影响程度由大至小依次为流体入射速度＞最小加工间隙＞喷射角度，其中流体入射速度对流场压力影响最为显著，而最小加工间隙在0.2～1.2 mm间对流场压力影响较小.实验中应严格控制流体入射速度以使抛光区域流场压力平稳，从而使工件获得高精度光洁表面.

4 抛光工艺参数对抛光效果的影响

实验选用直径为150 mm的K9玻璃进行加工.利用Bruker NPFLEX 3D Metrology System对抛光前的玻璃表面微观特性进行检测，检测范围为4.685 mm×3.514 mm，测量结果如图4所示.抛光前的玻璃表面粗糙度Ra＝0.481 6μm，峰谷高低差PV＝3.507 9μm.

在东华大学设计的混合磨料抛光设备上进行玻璃磨料流体抛光实验.实验中磨料选用氧化铝（粒度为D90＝12μm），p H值调节剂为氢氧化钠，基载液为去离子水，各种成分的质量分数分别为磨料10%、表面活性剂0.05%、p H值调节剂3%（p H值为11）.扫描模式为ρ-θ极轴扫描方式，工件转速为8 r／min，工作台平移速度为8 mm／min，其他抛光参数如下：射流靶距Ds＝15 mm，最小加工间隙h0＝0.8 mm，限控轮转动速度ω＝175 rad／s，矩形喷嘴尺寸为8 mm×1 mm，流体动力黏性系数μ＝0.005 Pa·s.

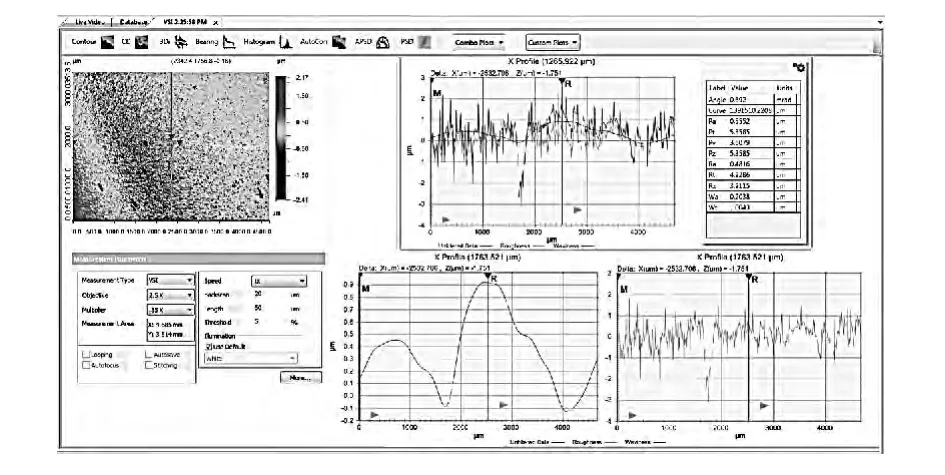
图4 磨料流体抛光前K9玻璃表面形貌Fig.4 K9 optical glass surface morphology before abrasive fluid polishing

4.1 流体入射速度u对抛光效果的影响

实验中流体喷射角度α＝30°，流体入射速度u分别为20，25，30 m／s，抛光时间为100 min，不同流体入射速度下的玻璃表面形貌如图5所示.由图5可以看出，流体入射速度u＝20 m／s时，Ra＝0.196 6μm，PV＝0.579 9μm；入 射速 度u＝25 m／s时，Ra＝0.156 7μm，PV＝0.504 4μm；入射速度u＝30 m／s时，Ra＝0.105 5μm，PV＝0.414 0μm.实验结果表明：在实验规定的入射速度范围内，随着流体入射速度的增加，玻璃表面粗糙度值和峰谷高低差值明显减小.

图5 不同入射速度下的玻璃表面形貌（α＝30°）Fig.5 Glass surface morphology at different injection velocity（α＝30°）

4.2 流体喷射角度α对抛光效果的影响

实验中流体入射速度u＝20 m／s，流体喷射角度α分别为30°，35°，40°，抛光时间为100 min，不同流体喷射角度下的玻璃表面形貌如图6所示.结合图6和5（a）可以看出，在流体喷射角度α＝30°时，Ra＝0.196 6μm，PV＝0.579 9μm；α＝35°时，Ra＝0.175 0μm，PV＝0.626 2μm；α＝40°时，Ra＝0.168 1μm，PV＝0.881 5μm.实验结果表明：在实验规定的喷射角度范围内，随着α的增大，玻璃的表面粗糙度值减小，但峰谷高低差值增大.这是因为流体喷射角度增大，使磨料射流中磨料的剪切力增大，对工件表面产生较大的剪切去除作用，对提高玻璃表面质量的效果反而不明显.

图6 不同喷射角度下的玻璃表面形貌（u＝20 m／s）Fig.6 Glass surface morphology at different jet incident angle（u＝20 m／s）

5 结 语

限控轮约束磨料流体抛光中，流体入射速度、喷射角度及最小加工间隙是影响抛光区域流体动压力及抛光效果的动态因素.本文利用Fluent仿真软件，对不同工艺参数的光学玻璃磨料流体抛光效果进行仿真分析，为磨料流体抛光玻璃提供依据.实验证明：增大流体入射速度能有效地提高抛光玻璃表面质量；在一定范围内增大喷射角度，玻璃表面粗糙度值减小，但峰谷高低差值随之增大.下一步研究将集中在抛光参数间的耦合效应分析、抛光质量的稳定控制方法及其实现技术方面.

［1］WALKER D D，FREEMAN R，GAVANA G，et al.The Zeeko／UCL process for polishing large lenses and prisms［C］／／SPIE，2002：106-112.

［2］KORDONSKI W I，JACOBS S D.Magnetorheological finishing［J］.International Journal of Modern Physics B，1996（10）：2837-2848.

［3］HASHISH M.Three-dimensional machining with abrasivewater jets［J］.Jet Cutting Technology，1992（13）：605-620.

［4］MORI Y，YAMAUCHI K，ENDO K.Elasitic emission machining［J］.Precision Engineering，1987，9（3）：123-128.

［5］PRESTON F.The theory and design of plate glass polishing machines［J］.J Soc Glass Technol，1927，11（44）：214-256.

［6］李长河，蔡光起，修世超，等.砂轮约束磨粒喷射加工接触区压力场建模与验证［J］.兵工学报，2007，28（2）：202-205.

［7］WILLIAMS J A，HYNCICA A M.Mechanisms of abrasive wear in lubricated contacts［J］.Wear，1992，152：57-74.

［8］计时鸣，於加峰，洪滔，等.槽形抛光工具形状对液流悬浮抛光加工效果的影响［J］.农业工程学报，2012，28（1）：87-90.

［9］陈伯贤，裘祖干，张慧生.流体润滑理论及其应用［M］.北京：机械工业出版社，1991：13-26.

［10］CHEN W L.Turbulence modeling for highly-loaded cascade blades［D］.UMIST，Manchester，UK，1996.

Experimental Investigation and Flow Field Analysis of Abrasive Fluid Polishing

YANRu-zhong，GANMin-hua，LIUZhen-tong

（College of Mechanical Engineering，Donghua University，Shanghai 201620，China）

The impact trend of process parameters in abrasive fluid polishing of optical glass is investigated through Fluent simulation，which is based on hydrodynamic pressure theory andκ-εturbulent model.The results show that the hydrodynamic pressure is directly proportional to injection velocity and inversely proportional to minimum clearance between wheel and work piece.Pressure increases gradually along the constrained wheel rotation direction，and it reaches a maximum value before the minimum clearance.It can also be concluded that the peak pressure is generated when the fluid incident angle is 45°.The theoretical model based on theκ-εturbulent model and the Navier-Stokes equations is in agreement with the simulation results.The surface features of polished K9 optical glasses are investigated experimentally.The results show that the surface characteristic values of workpieces improve substantially while the fluid injection velocity increases.

abrasive fluid polishing；turbulent model；Fluent simulation；hydrodynamic pressure

TG 580.692

A

2013-05-15

闫如忠（1966—），男，河南淮阳人，副教授，博士，研究方向为光学玻璃精密抛光.E-mail：yanrz＠dhu.edu.cn

1671-0444（2014）03-0329-05