7050铝合金内部沿晶微裂纹热塑性修复的元胞自动机模拟
马 凯,张效迅,李 霞,马 芳
(1. 上海工程技术大学 材料工程学院,上海 201620;2. 上海工程技术大学 汽车工程学院,上海 201620)
金属材料加工过程所涉及的成形工艺以及后期构件在使用过程中的服役条件,都会或多或少的给构件带来各种各样的缺陷,如缩孔、缩松、微空洞、微裂纹等。尤其,当含孔洞型缺陷(空洞或裂纹)的构件在受到拉/压力造成局部应力集中时,材料内部组织的连续性可能随着空洞/裂纹的应力撕裂而遭到破坏,其后果所导致的构件断裂或寿命下降是很严重的。所以,如何将内裂纹予以修复,使金属材料的内部微观组织实现连续,对提高构件寿命以及保障工程安全有着重大的意义。
从当前的报道来看,现已有很多课题组对裂纹的修复工作展开研究:张永军等[1]、韦东滨等[2−4]不仅研究了裂纹愈合及愈合带的形貌特征,而且利用分子动力学法模拟了纳观尺度的裂纹愈合情况;张海龙等[5−6]对纯铁与纯镁内部穿晶和晶内疲劳裂纹的修复机理进行了研究,建立了体扩散下的空洞收缩模型;张效迅等[7−8]针对材料内部空洞闭合以及其演化规律做了相关的探索。总体上看,大部分研究人员都是从物理实验来展开裂纹愈合的研究工作,而模拟手段仅有张永军等[1]采用的分子动力学法有见报道,虽然分子动力学的模拟是基于纳观尺度,研究了更微小裂纹的演变规律,但热塑性愈合条件下伴随有组织演变的裂纹修复过程,分子动力模拟法未予以表示,并且为了制备出更符合实际的裂纹形貌特征,包括穿晶、沿晶、晶内裂纹等形式,分子动力学在裂纹的模拟编制方面也显示了其局限性。
近几十年来,随着计算机的发展以及材料科学理论的不断完善,元胞自动机(CA)法对于金属材料微观组织演变过程的模拟愈发成熟,本工作以航空 7050铝合金作为模拟材料,对热塑性条件下的裂纹修复过程进行了CA模拟,探索了温度、应变对裂纹愈合的影响规律。此种方法十分新颖,国内外尚未有所报道,CA模拟不仅再现了动态再结晶对裂纹修复的整个过程,填补了材料缺陷模拟的不足,同时也为材料内缺陷的演变修复模拟探索方向以及软件的开发提供了新思路和技术指导。
1 7050铝合金材料CA参数辨识
物理实验数据由 Gleeble−3500热模拟机对 7050铝合金d8 mm×10 mm棒状试样的等温压缩实验来提供,热塑性压缩工艺为:以5 ℃/s 的加热速度分别对试样加热至250、300、350、400和450 ℃,保温3 min后,在各个变形温度下,分别以0.01、1和10 s−1的应变速率对试样进行压缩,使其真应变达到0.8,变形结束后,立即淬火,保留试样热变形微观组织,得到的真应力—应变曲线如图1。
通过对物理实验数据进行合理的处理,得到的7050铝合金热塑性变形的本构方程如下[9]:
1)Z参数—应变速率方程


图1 7050铝合金热压缩流变应力曲线Fig. 1 Stress—strain curves of 7050 aluminum alloy during hot compression: (a) ε˙=0.01 s−1; (b) ε˙=1 s−1; (c) ε˙=10 s−1
2) 应力应变速率方程
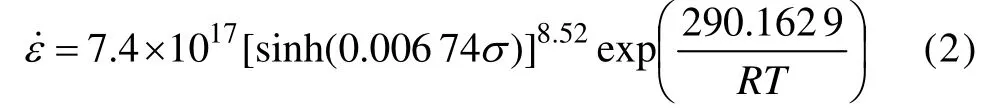
3) 峰值流变应力方程

由式(2)可得到 7050铝合金的动态再结晶热激活能Qact=290.16 kJ/mol。DING等[10]认为,再结晶形核率与温度和应变速率有关:

式中:C和m为材料参数,本工作采用反分析法[11−12]求得不同变形条件下的C、m值,最后建立不同条件下的形核模型。
微观组织演化的另外两个重要参数分别是加工硬化系数k1和动态回复软化系数k2。采用KM模型建立的位错密度模型为[13]

式中:ρ为任意时刻位错密度值,对上式积分,当满足极限条件时,可求得流变应力的外延饱和位错密度:

当应变条件为ε<cε时,k2可由外延饱和应力方程求得,其表达式为
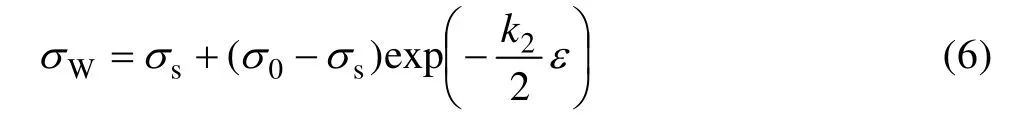
式中:Wσ是外延饱和应力,低于临界应变时,其为真实值,高于临界应变时,其为虚拟值,用于对稳态流变应力的求解;cε是临界应变;0σ为零载荷条件下的内应力;sσ为饱和应力,其值可由加工硬化率—真应力曲线的平滑延伸线和真应力轴的交点来求得。结合Taylor公式和饱和流变应力sσ,建立k1、k2
的关系式如下:
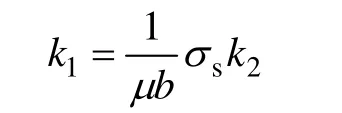
式中:b为Burger’s矢量模;μ为剪切模量,这样k1的值亦可求得。
2 沿晶裂纹CA模型
2.1 应变驱动的拓扑变形演化规则
热塑性变形对于裂纹修复愈合的影响不仅仅取决于外界能量输入的方式和大小,裂纹的形貌特征,包图2中:i、j分别为Microsoft Visual C++平台上MFC窗口的显示方向,两者相互垂直。括大小、形状、位置等对愈合的效果也有重要影响。从原子扩散以及界面迁移的角度上讲,裂纹面贴合愈近,晶粒长大接触的距离就越小,再结晶晶面的碰撞结合时间就越短,所以只有当所编制的元胞自动机(CA)演化规则中包含有裂纹母相组织随应变增加而不断演化的拓扑变形特征时,才能反映材料内部真实的物理状况。
基于形变拓扑理论,对正方形元胞做相应处理,其流程图如图2所示。
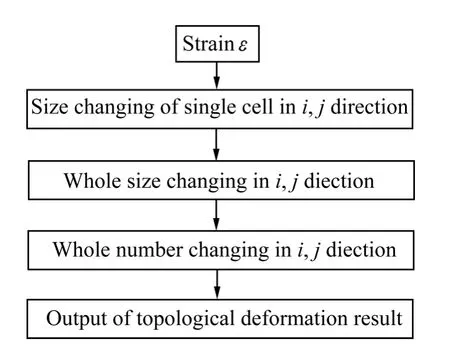
图2 拓扑演化原理流程图Fig. 2 Flow chart of topology evolution principle
2.2 沿晶裂纹设计
金属材料内部微裂纹主要的形式为穿晶裂纹、沿晶裂纹、晶内裂纹3种。本文作者采用“晶粒抠除法”设计沿晶裂纹。将某一个晶粒用可控制的 RGB颜色通道显示驱动,使其在 MFC控制显示窗口中与白色母相基体组织区分开来。图3所示为平均晶粒尺寸为225 µm的内裂纹母相组织模拟图,其中深色部分为裂纹空腔,总元胞规模为200×200个,每个元胞代表实际材料面积 2 µm×2 µm。

图3 含沿晶裂纹的母相组织Fig. 3 Parent phase structure including intergranular crack
2.3 CA模型的建立
动态再结晶的形核条件为热塑性变形驱动的位错密度或应变达到临界值,临界位错密度与临界应力又遵循Taylor关系式。为建立完整含裂纹的CA模型,本文作者提出如下假设:
1) 裂纹空腔的位错密度和取向均为0,将其作为无物质真空状态考虑,裂纹边界为自由表面;
2) 微观尺度裂纹的存在不影响发生动态再结晶的临界位错密度和临界应变值;
3) 动态再结晶同时发生于裂纹表面与晶界处,形核遵循晶界弓出形核机制[14]。
结合所得参数以及对裂纹区域描述的假设,利用Microsoft VC++平台对含裂纹的动态再结晶CA演化规则进行程序编制,详细的流程如图4所示。
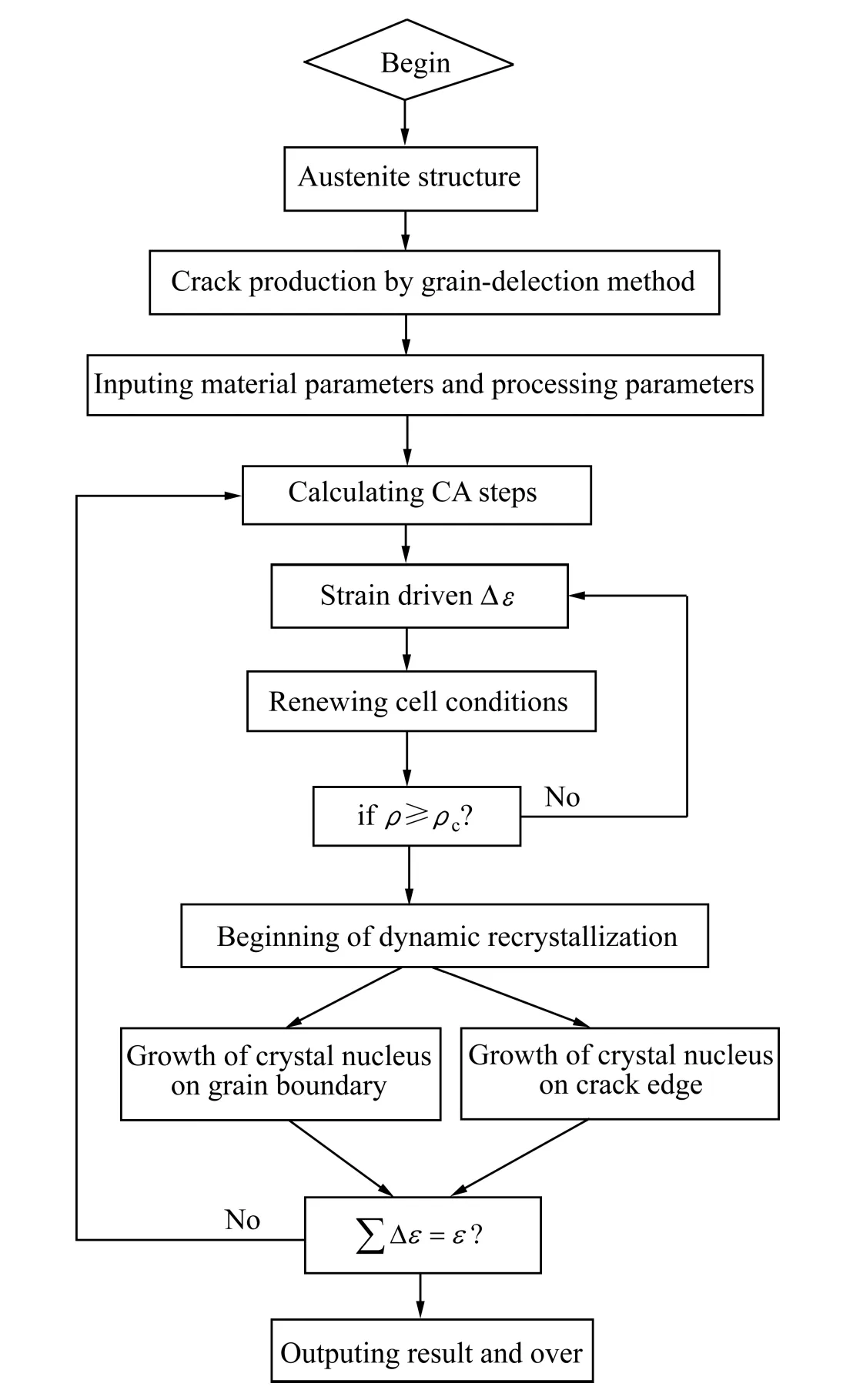
图4 CA模拟流程图Fig.4 CA simulation flow chart
3 裂纹修复的能量驱动机制
内裂纹的存在,使得材料系统内部变得不连续,裂纹面不同于晶粒之间的晶界特性,这决定了在再结晶形核长大时,不同位置的驱动力形式必须加以区分。如图5所示,晶界弓出生长机制描述了在晶界位置A处形核后,晶界的迁移方向指向位错密度高的一侧,晶界迁移方向与位错密度梯度方向相反,新核每长大dr尺寸的半径,能量的变化值表达式为
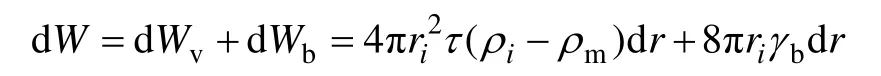
作用于晶界单位面积的驱动力大小为
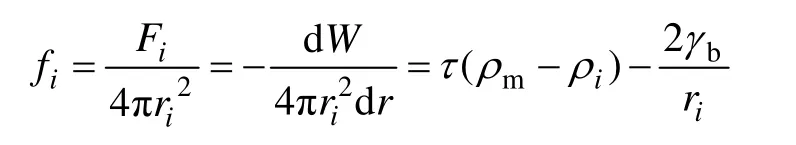
晶界弓出机制描述了再结晶晶粒长大速度与作用于晶界上的单位面积驱动力fi的关系为
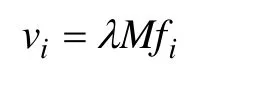
以上公式中,dWv、dWb分别为晶粒长大dr半径的体积能和晶界能改变量;iρ、mρ分别为再结晶元胞及其相邻母相元胞的位错密度值;γb是晶界能;M是晶界迁移率;Fi为施予晶界面的总力;fi为单位晶界面积的受力值;λ为考虑合金元素对晶粒长大影响的参数,纯金属一般取1=λ;vi是再结晶晶界迁移速度;ri为再结晶晶粒的半径值,其求解方式为,∑iS为再结晶晶粒包含元胞的面积之和。
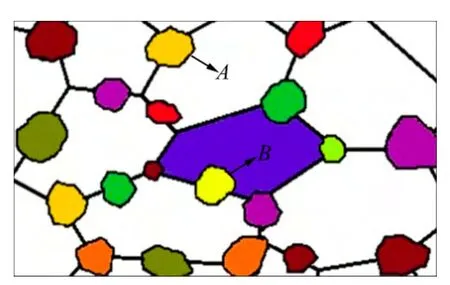
图5 不同晶粒的生长模式与驱动机制图Fig. 5 Growth pattern and driving mechanism maps of different grains
对不同位置的晶核长大驱动力进行分析,可以发现:在图5中的A处,晶界形核以及其后长大对母相的吞并过程,其实际驱动力完全是依靠母相的位错密度释放而补给的,新晶核的晶界形成能γb对晶粒长大起阻碍作用。当晶核朝裂纹空腔处生长时,在图5中的B处,再结晶晶核增长dr半径的驱动力是新核内原子的热扩散运动所驱动,其结果是使晶核半径尺寸由ri变为ri+dr。因此,由晶核系统能量的增量来看,驱动力的大小应该为表面能的增量,且此过程仅仅是表面的迁移运动,不同于母相内部畸变能的位错密度释放过程。由于在此方向上不存在新核吞并母相晶粒的现象,所以将体积能释放的驱动力部分予以忽略,故晶粒向裂腔处长大的单位表面积驱动力应表示为
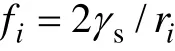
式中:γs为固体表面能值。参考陆海鸣[15]对表面弛豫现象下金属材料固体表面能对于界面/表面尺寸大小依赖的探究结果,本研究取固体表面能值为2 J/m2对7050铝合金进行裂纹热塑性愈合的 CA模拟探索与分析。
4 裂纹修复CA模拟结果及分析
图6所示为真应变分别为0.4、0.6、0.8的裂纹拓扑变形CA模拟示意图。从变形特征可以看出,与初始组织中的裂纹形貌(见图3)相比,二维近似椭圆状的裂纹型腔随塑性变形的增加,逐渐演化为长条形状的扁平裂纹,裂纹的长度被拉长,宽度最大距离由初始的Wcrack_max=48Lca(见图3)变为真应变条件下最大宽度Wcrack_max=21Lca(见图 6(c)),其中Lca是单个元胞的边长。
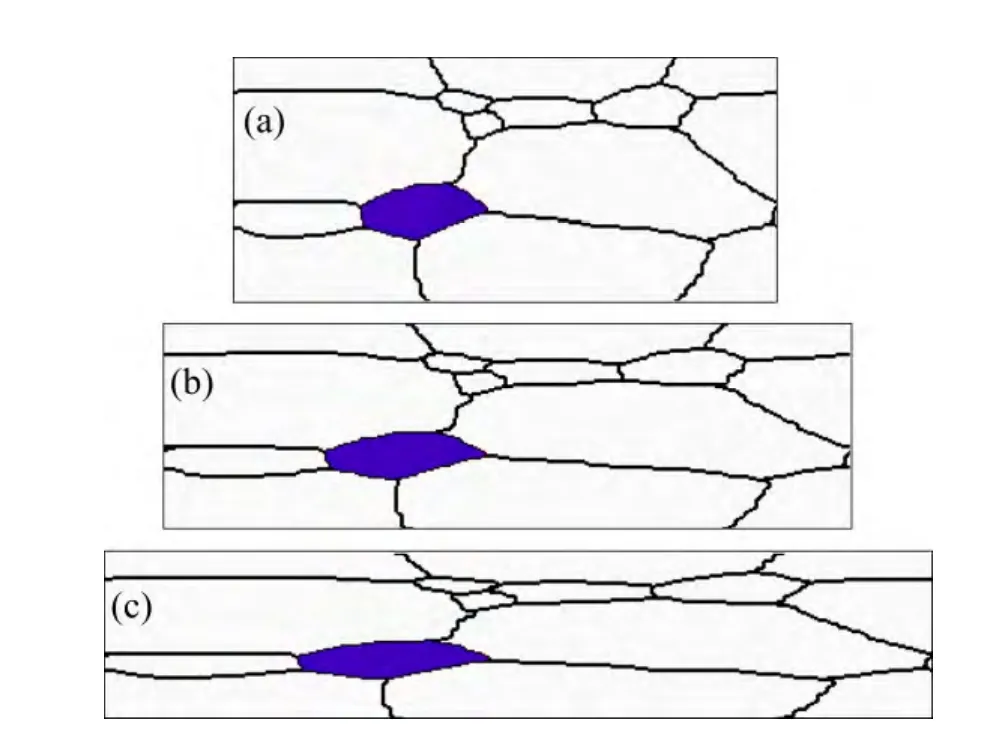
图6 不同应变条件下的裂纹形貌演化Fig. 6 Evolutions of crack morphology under different strain conditions: (a) ε=0.4; (b) ε=0.6; (c) ε=0.8
在623 K、应变速率01.0=ε˙s−1、真应变分别为0.4、0.6、0.8、1.0、1.2的条件下进行裂纹愈合模拟,得到如图7所示的模拟结果。可以看出,在等应变速率的条件下,随着塑性应变量的增加(a→e)再结晶形核数目及形核数量逐渐增多,形核位置优先分布在裂纹面和晶界的交界处,这是因为裂纹表面和晶界的交界随机形核率大的缘故。
由模拟结果可知,拓扑变形减小了晶粒长大接触的距离和时间,对裂纹面的贴合以及最终的修复起到促进作用。在CA模拟代表的真实物理时间内,随着应变的增加,裂纹边界弓出形核长大的晶粒数目增多,且在二次结晶的表面上又有新核的形成与长大(见图7(c))。在母相内部再结晶分数随着塑性变形量的增加而变大的同时,再结晶晶粒对裂纹空腔的占有面积不断变化,特别是在裂纹表面和晶界交界处,不断长大的晶粒逐渐将扁平形貌的裂纹演化为球状的空洞形式(见图 7(d)),裂纹愈合的效果越来越好,当塑性真应变为ε=1.2时(见图7(e)),裂纹完全被再结晶晶粒所修复,母相基体重新被均匀化的细晶组织覆盖,CA模拟再现了金属材料由不连续到连续的过程。

图7 应变速率0.01 s−1,温度623 K条件下不同应变对裂纹愈合的影响Fig. 7 Effects of different strains on crack healing under conditions of strain rate 0.01 s−1 and temperature 623 K:(a) ε=0.4; (b) ε=0.6; (c) ε=0.8; (d) ε=1.0; (e) ε=1.2
图8 所示为真应变1.0时,温度分别为573 K、623 K、673 K条件下的裂纹愈合CA模拟形貌。由模拟结果可知,等应变条件下,再结晶晶粒尺寸以及再结晶分数随温度的增加而变大,裂纹的愈合效果越来越好。573 K时,再结晶晶粒的形核和接触长大将扁平裂纹分成大小不同的左右两段(见图8(a)),裂纹出现分段演化的形貌特征,这一特征与韦东滨[4]和张海龙等[5−6]的实验结论相吻合。同样的应变和应变速率条件下,温度623 K(见图8(b))时裂纹愈合形貌却未出现分段的特征,扁平的裂纹由于不断的晶粒长大结果而演变为单一的微小孔洞模型。分析模拟机制,这是因为CA模拟是应变控制的动态再结晶过程,演化结果覆盖了演化的整个过程,所以“分段愈合”特征不是裂纹愈合所必然出现的一种演化规律,其只是某一演化阶段的裂纹存在形式,具体的裂纹愈合的形貌演化主要取决于裂纹形态、裂纹表面形核率和形核位置、新晶粒长大方向与速度。图8(c)最终表明673 K条件下塑性真应变为1.0的物理时间内,动态再结晶也可以实现对微裂纹的完全修复,这和图 7(e)的效果是一样的,但值得指出的是,由于愈合后愈合温度过高以及保温时间的增加都会使材料内部留下较为粗大的晶粒组织,所以如何控制温度对热塑性愈合后的组织性能影响同样是很重要的。

图8 应变速率0.01 s−1和真应变1.0条件下不同温度对裂纹愈合的影响Fig. 8 Effects of different temperature on crack healing under conditions of true strain 0.01 s−1 and rate strain 1.0: (a) 573 K;(b) 623 K; (c) 673 K
4 结论
1) 基于裂纹周围不同晶粒的生长模式与驱动机制,在Microsoft Visual C++ 编程平台上,建立了包含拓扑变形机制、位错密度演变机制、动态再结晶动力学机制的模拟沿晶裂纹热塑性修复的CA模型,实现了动态再结晶条件下裂纹愈合形貌演化的模拟。
2) CA模拟结果表明,温度和应变对裂纹愈合有重要影响,在一定的温度和变形条件下,可以完全实现对沿晶微裂纹的修复,且合适的温度和保温时间是保持材料内部晶粒均匀细化的关键。
3) 在一定条件下,裂纹愈合会呈现出分段愈合特征,但裂纹分段愈合现象非必然的,裂纹愈合的形貌演化取决于裂纹形态、裂纹表面形核率和形核位置、新晶粒长大方向与速度。
[1]ZHANG Y J, HAN J T. Analysis of microstructure of steel 20 in the rang of healing of internal crack[J]. Metal Science and Heat Treatment, 2012, 53(11): 526−528.
[2]韦东滨, 韩静涛, 谢建新, 付晨光, 王连忠, 贺毓辛. 热塑性变形条件下钢内部裂纹愈合的实验研究[J]. 金属学报, 2000,36(6): 622−625.WEI Dong-bin, HAN Jing-tao, XIE Jian-xin, FU Chen-guang,WANG Lian-zhong, HE Yu-xing. Experimental study on inner crack healing in steel during hot plastic deforming[J]. Acta Metallurgica Sinica, 2000, 36(6): 622−625.
[3]WEI D B, JIANG Z Y, HAN J T. Modelling of the evolution of crack of nanoscale in iron[J]. Computational Materials Science,2013, 69: 270−277.
[4]韦东滨. 金属材料内部裂纹愈合规律的研究[D]. 北京: 北京科技大学, 2001.WEI Dong-bin. Research on the disciplinarian of inner crack healing in metal[D]. Beijing: Beijing University of Science and Technology, 2001.
[5]张海龙, 杨君刚, 孙 军. 工业纯铁内部穿晶疲劳微裂纹的扩散愈合过程[J]. 金属学报, 2002, 38(10): 1015−1020.ZHANG Hai-long, YANG Jun-gang, SUN Jun. Diffusive healing of transgranular fatigue microcracks withinα-iron[J].Acta Metallurgica Sinica, 2002, 38(10): 1015−1020.
[6]杨君刚, 张海龙, 孙 军. 工业纯镁内部疲劳微裂纹的热扩散性愈合[J].金属学报, 2005, 41(8): 819−823.YANG Jun-gang, ZHANG Hai-long, SUN Jun. Diffusive healing of internal fatigue microcracks in pure magnesium[J].Acta Metallurgica Sinica, 2005, 41(8): 819−823.
[7]ZHANG X X, CUI Z S, CHEN W, LI Y. A criterion for void closure in large ingots during hot forging[J]. Journal of Materials Processing Technology, 2009, 209(4): 1950−1959.
[8]张效迅, 崔振山. 大锻件内部空洞热锻闭合的 Z-C判据及其应用[J]. 机械工程学报, 2009, 45(1): 148−152.ZHANG Xiao-xun, CUI Zhen-shan. Z-C criterion of void closure for large-ingot hot forging and its application[J]. Journal of Mechanical Engineering, 2009, 45(1): 148−152.
[9]SELLARS C M, ZHU Q. Microstructural modeling of aluminium alloys during thermomechanical processing[J].Materials Science and Engineering A, 2000, 280: 1−7.
[10]DING R, GUO Z X. Microstructural modeling of dynamic recrystallization using an extended cellular automaton approach[J]. Computational Materials Science, 2002, 23:209−218.
[11]JIN Zhao-yang, LIU Juan, CUI Zhen-shan, WEI Dong-lai.Identification of nucleation parameter for cellular automaton model of dynamic recrystallization[J]. Transactions of Nonferrous Metals Society of China, 2010, 20(3): 458−464.
[12]金朝阳, 崔振山. Q235动态再结晶微观组织演化模型及其参数辨识[J]. 热加工工艺, 2010, 39(24): 33−37.JIN Zhao-yang, CUI Zhen-shan. Microstructure evolution model for Q235 under dynamic recrystallization and its parameter identification[J]. Hot Working Technology, 2010, 39(24):33−37.
[13]陈 飞. 热锻非连续变形过程微观组织演变的元胞自动机模拟[D]. 上海: 上海交通大学, 2012.CHEN Fei. Simulation of microstructure evolution during discontinuous hot forging processes using cellular automaton method[D]. Shanghai: Shanghai Jiao Tong University, 2012.
[14]马 凯, 张效迅. 元胞自动机法在裂纹愈合模拟中的应用[J].精密成形工程, 2012, 4(6): 45−49.MA Kai, ZHANG Xiao-xun. The application of cellular automaton method in crack healing simulation[J]. Journal of Netshap Forming Engineering, 2012, 4(6): 45−49.
[15]陆海鸣. 尺寸依赖的界面能[D]. 长春: 吉林大学, 2006.LU Hai-ming. Size-dependent interface energy[D]. Changchun:Jilin University, 2006.

