自适应收扩系数的双中心协作QPSO算法
丁 颖,李 飞
自适应收扩系数的双中心协作QPSO算法
丁 颖a,李 飞b
(南京邮电大学 a. 通信与信息工程学院;b. 信号处理与传输研究院,南京 210003)
针对量子粒子群优化(QPSO)算法迭代后期种群多样性下降、收敛速度慢、易陷入局部最优的缺点,提出一种自适应收缩-扩张系数的双中心协作量子粒子群优化算法。该算法从2个方面进行改进:(1)自适应调节收缩-扩张系数,其目的是帮助粒子跳出局部最优点,提高粒子的全局搜索能力;(2)双重更新全局最优位置,即在每次迭代中,先后分别采用2种不同的方式更新全局最优位置。第1种方式与QPSO算法一致,第2种方式则引入双中心粒子,使其和当前全局最优位置在相应维度上合作,从而达到更新全局最优位置的目的。从固定迭代次数和固定精度角度分析算法性能,仿真结果表明,相比于QPSO算法,该算法在保证复杂度较低的情况下,可提高收敛速度,增强全局和局部搜索能力。
量子粒子群优化算法;收缩-扩张系数;双中心粒子;协作;全局最优位置
1 概述
量子粒子群优化(Quantum Particle Swarm Optimization, QPSO)算法[1]是Sun等人于2004年从量子力学的角度提出的一种新型的粒子群优化算法。相对于传统的粒子群优化算法(Particle Swarm Optimization, PSO),该算法具有搜索范围广、收敛速度快、寻优精度高的特点,但对于复杂问题仍然容易陷入局部最优。近年来,对QPSO的研究主要有以下3个方面:(1)理论的证明和研究[2-4]。(2)改进收缩-扩张系数[5-6]。文献[5]提出系数非线性变化的策略,其寻优能力优于线性变化的情况。(3)与其他算法的融合[7-9]。文献[7]提出将遗传算法的选择和变异操作融入到QPSO中,提高了收敛速度,改善了早熟问题。文献[8]将一种调和算法和QPSO结合,提出一种改进的量子粒子群算法(HQPSO)。与标准QPSO算法相比,该算法搜索能力更强、收敛速度更快。
文献[10]提出双中心粒子的思想,并利用该思想优化粒子群算法,但并未充分利用该双中心粒子。本文将该思想应用到量子粒子群优化中,提出自适应收扩系数的双中心协作QPSO(AQPSO)算法,使双中心粒子和当前全局最优位置在相应维度上合作[11],并设计双重更新全局最优位置的策略,以提高算法的寻优能力和收敛速度。
2 QPSO的基本原理
PSO是一种模拟鸟群捕食的群智能算法[12],具有参数少、效果好的优点,但也存在不足,如搜索范围受限,不能保证以概率1收敛到全局最优点等。QPSO是Sun等人于2004年在PSO的基础上从量子力学的角度提出的一种新型的优化算法,不仅具有PSO的优点,而且理论上能够保证全局收敛。
在QPSO中,用波函数(,)描述粒子的状态,粒子的位置由波函数来决定:
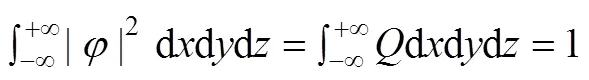
其中,表示粒子在时刻出现在点(,,)的概率密度,通过求解薛定谔(Schr dinger)方程可以得到。粒子位置通过蒙特卡罗(Monte Carlo)随机模拟的方式得到,其更新方程如式(2)~式(6)所示。
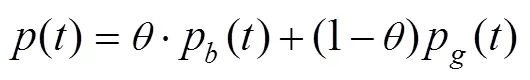
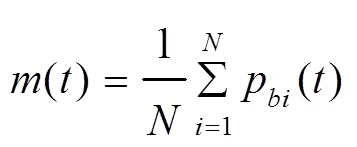
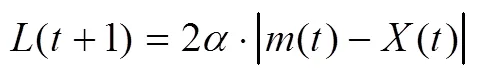
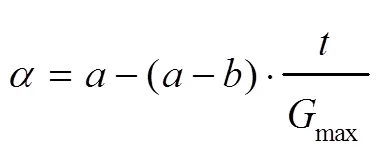
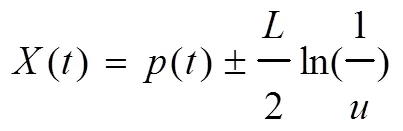
其中,p()和p()分别代表粒子在第次迭代时的个体最优位置和种群的全局最优位置;是在[0,1]上服从均匀分布的随机数;()为粒子第次迭代的局部吸引域,表示的是每个粒子介于个体最优位置和全局最优位置之间的随机位置;表示粒子与种群平均最优位置的带权距离;是在[0,1]上服从均匀分布的随机数;称为收缩-扩张系数,用来控制粒子的收敛速度,随着迭代的进行,线性地从变化到[13],通常=1,=0.5;max表示最大的迭代次数。
综合式(2)~式(6)可得:
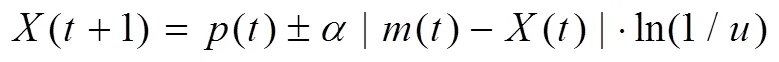
此外,以求函数最小值为例,个体最优位置和全局最优位置的更新公式如式(8)和式(9)所示,其中,=1,2,…,。
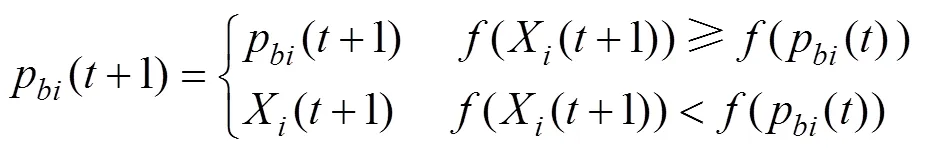
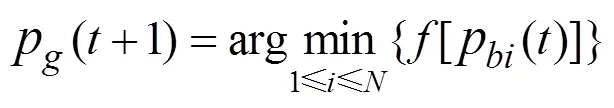
3 AQPSO的基本原理和算法流程
3.1 AQPSO的基本原理
3.1.1 自适应收缩-扩张系数
根据式(5),标准QPSO中的收缩-扩张系数是随着迭代次数的增加而线性递减,而实际的搜索过程是非线性的,所以,不能适应复杂的非线性寻优过程。文献[14]证明当<1.7时,粒子收敛于当前全局最优位置;当>1.8时,粒子发散,将逃离全局最优位置区域。本文对的改进算法[15]如下:
If fitness(xi)==0
then hi=1
else hi=fitness(pg)/fitness(xi)
Endif
hmax=max(hi)
hmin=min(hi)
If hmax==hmin
thenai=amin+(amax–amin)*hmax
elseai=(amax–amin)/(hmax–hmin)*hi+(amin*hmax–amax*hmin)/
(hmax– hmin)
Endif
说明:该算法的适用前提是求解函数的最小值,并且最小值均非负;x表示第个粒子的位置,=1,2,…,;=()表示适应度函数,即需要被优化的目标函数,因此,(x)表示x的适应度函数值;p表示全局最优位置;h表示当前全局最优位置的适应度函数值和当前第个粒子的适应度函数值的比值;max和min分别表示所有粒子中的最大值和最小值;max=1.7,min=0.5。
α和h的关系如图1和图2表示。
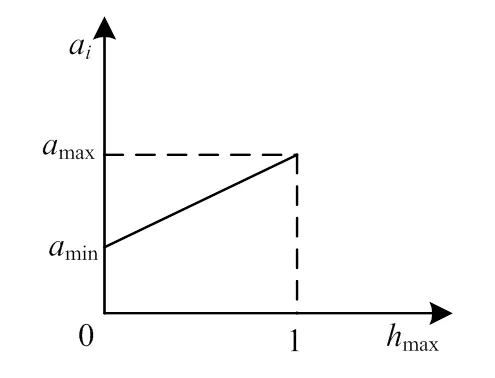
图1 hmax==hmin时αi的值
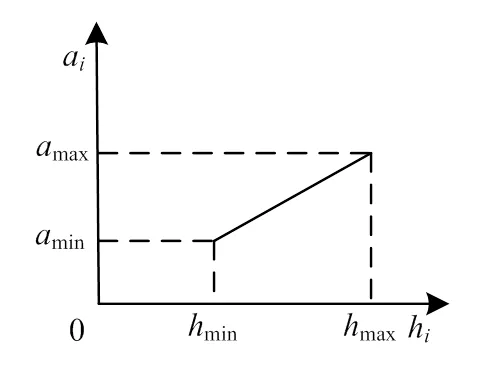
图2 hmax≠hmin时αi的值
由算法可知,h在0~1之间,h越大,表明该粒子越靠近全局最优位置,此时α越大,其跳出局部最优的能力越强;反之,α越小,加速收敛。由此可知,该算法能够保证每个粒子更好地自适应调节各自的值,避免陷入局部最优,从而提高了搜索寻优能力。
3.1.2 双重更新全局最优位置策略
由标准QPSO基本原理知,全局最优位置p是一个至关重要的位置[16],它指引着整个种群向最优解靠近,影响着最优解的质量和整体的收敛速度。文献[10]提出了双中心粒子群优化算法,并用实验验证了该算法的优势,但并未充分利用该双中心粒子。本文受文献[10]启发,提出双重更新全局最优位置的思想。第1种更新方式和QPSO一致。在第2种方式中,将双中心思想从PSO移植到QPSO中,通过双中心粒子和当前全局最优位置在相应维度上合作来更新全局最优位置。每次迭代先后分别应用这2种方式。下文主要介绍第2种更新方式。
双中心粒子-广义中心粒子(x)和狭义中心粒子(x)(分别为当前所有粒子个体最优位置中心和所有粒子当前位置中心),在本质上和其他粒子相同,是群体的组成部分,参与粒子间的共存与合作、个体优劣的比较以及全局最优位置的竞争等行为。其更新方式如式(10)和式(11)所示。
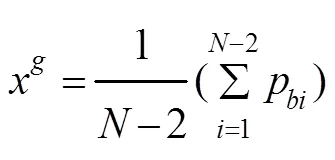
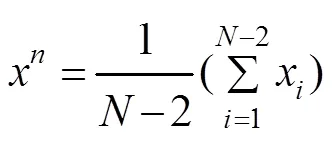
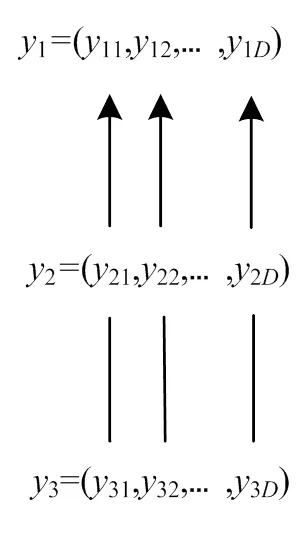
图3 粒子间合作示意图
首先,在1、2、3中选择适应度最优的位置,不妨设为1;其次,对于1的每一维度,分别用其他2个位置的相应维度值进行替换,若替换后的位置更加优秀,则用该位置更新1。例如,分别用21、31替换11可分别得到1’=(21,12,13,…,1D)、1’’=(31,12,13,…,1D),将它们和1= (11,12,13,…,1D)进行比较,选择三者中最优的位置,不妨设1’最优,则用1’更新1,其他维度同理合作。最后,利用最终得到最优位置更新p。
3.2 AQPSO算法流程
AQPSO算法具体步骤如下:
Step1置迭代次数=0;初始化种群规模;随机初始化前–2个粒子的位置x,=1,2,…,–2,以及个体最优位置p=x(=1,2,…,–2);由式(10)和式(11)计算得到双中心粒子的初始位置x(=–1,),并初始化双中心粒子的个体最优位置p=x(=–1,);根据式(9)求出初始全局最优位置。
Step2根据3.1.1节中的方法计算,并更新前–2个粒子的位置x(=1,2,…,–2)。
Step3计算前–2个粒子的适应度函数值。
Step4分别由式(8)、式(9)更新前–2个粒子的个体最优位置p(=1,2,…,–2),以及全局最优位置p。
Step5由式(10)和式(11)更新双中心粒子的位置x,=–1,。
Step6计算双中心粒子的适应度函数值。
Step7类似Step4,更新双中心粒子的个体最优位置p,i=–1,,以及全局最优位置p。
Step8利用3.1.2节的第2种方式更新p。
Step9判断是否达到终止条件,若否,置=+1,返回Step2;否则算法结束。
4 性能测试与结果分析
4.1 测试函数
本文采用4个测试函数,具体特点如表1所示。
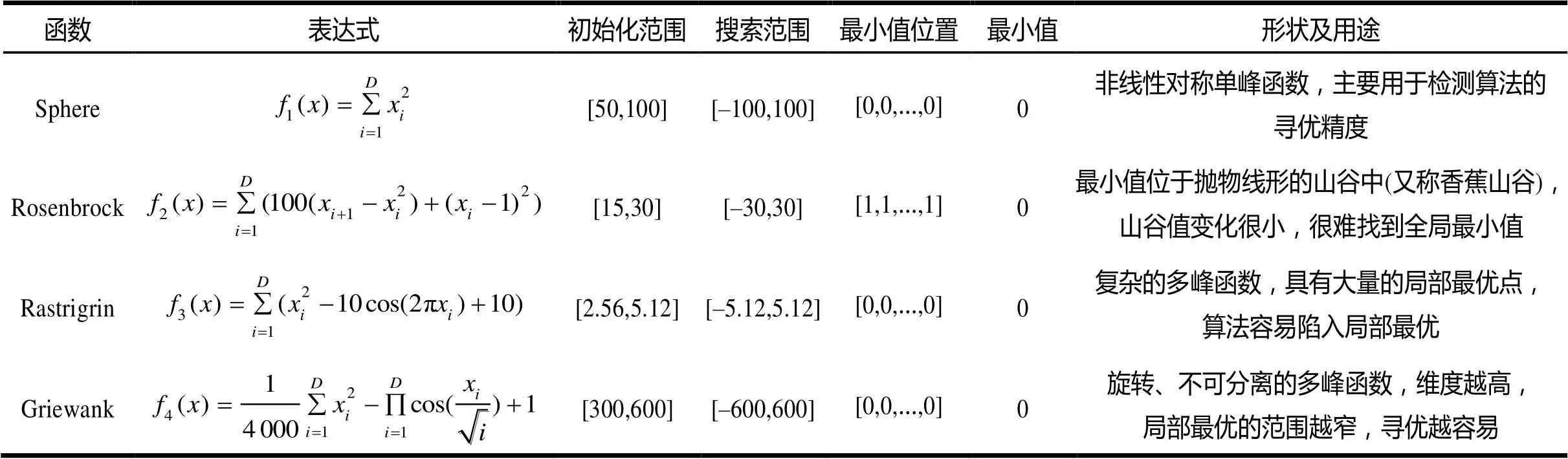
表1 测试函数
4.2 固定迭代次数的测试结果与分析
参数设置如下:粒子数=20;运行50次;维度用表示;最大迭代次数用max表示。
测试结果见表2和图4~图7。由表2可以看出,对于1,AQPSO优于QPSO和DQPSO。对于2,低维时,AQPSO的平均值稍优,最优值稍逊,但是最差值和标准差远远胜出;高维时AQPSO较优。对于3,当迭代次数稍大于1 000时,AQPSO的最优值急剧下降,并很快找到最优值0,这是因为3虽然具有很多的局部最优点,但其图形整体轮廓简单,不像2那样最优值位于形状复杂的谷底,该实验结果同时也验证了AQPSO算法在迭代后期克服局部最优的能力远胜于QPSO和DQPSO。对于4,低维时,AQPSO优于另外2种算法;高维时,AQPSO稍逊。由图4~图7可以看出,AQPSO的收敛速度和寻优能力优于其他2种算法。因此,固定迭代次数时,AQPSO性能远远优于QPSO和DQPSO算法。
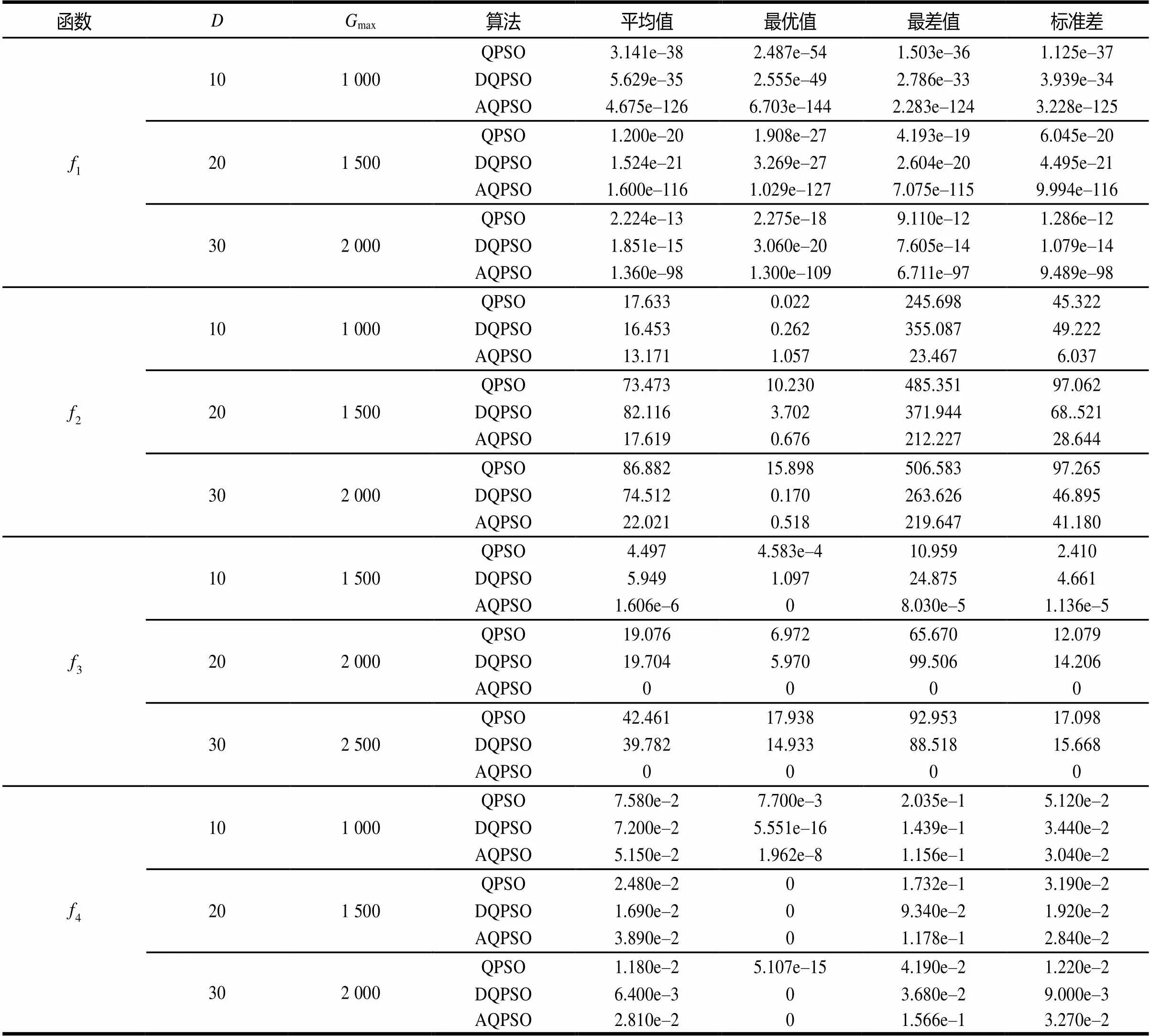
表2 固定迭代次数的仿真结果
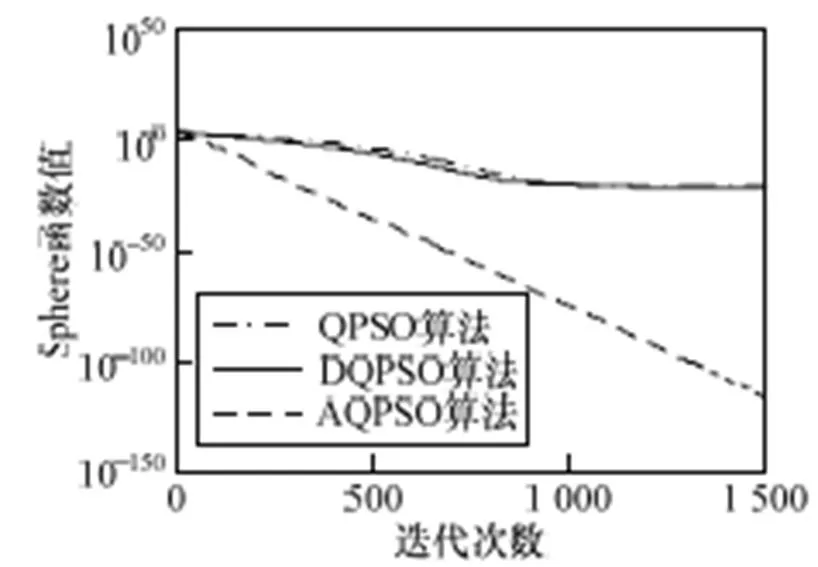
图4 Sphere函数测试结果(维度20,迭代1 500次)
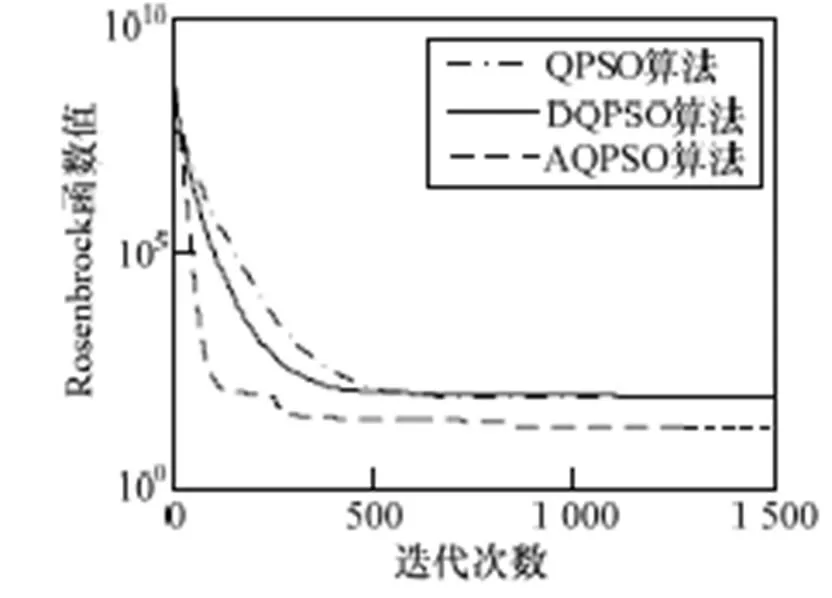
图5 Rosenbrock函数测试结果(维度20,迭代1 500次)
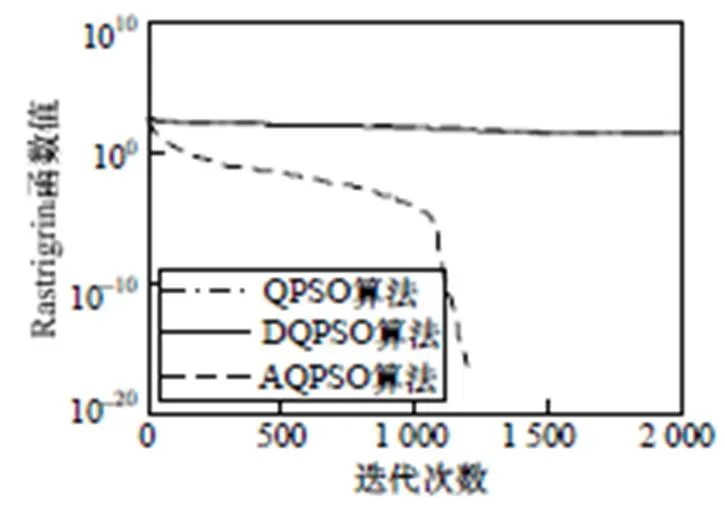
图6 Rastrigrin函数测试结果(维度20,迭代2 000次)
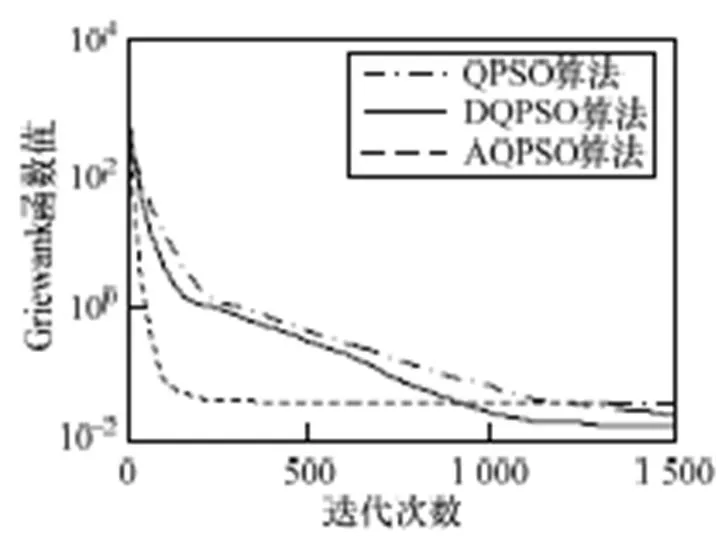
图7 Griewank函数测试结果(维度20,迭代1 500次)
4.3 固定精度的测试结果与分析
参数设置:粒子数=20,运行50次;1的终止精度为10–10,2终止精度为20,3的终止精度为0.1,4的终止精度为0.1。测试结果如表3所示,其中,平均迭代次数指在50次的运行中,达到指定精度时的平均迭代次数;平均时间指在50次的运行中,达到指定精度时所消耗的平均时间;成功次数指50次运行中,在最大迭代次数的限制下,能够成功达到所需精度的次数;失败次数=50–成功次数。
由表3可以看出,对于1、3、4,AQPSO的性能明显优于其他2种算法;对于2,在平均迭代时间上三者算法相差不大,但AQPSO的成功次数远大于另外2种算法。因此,固定精度时AQPSO算法的性能优于QPSO和DQPSO算法。
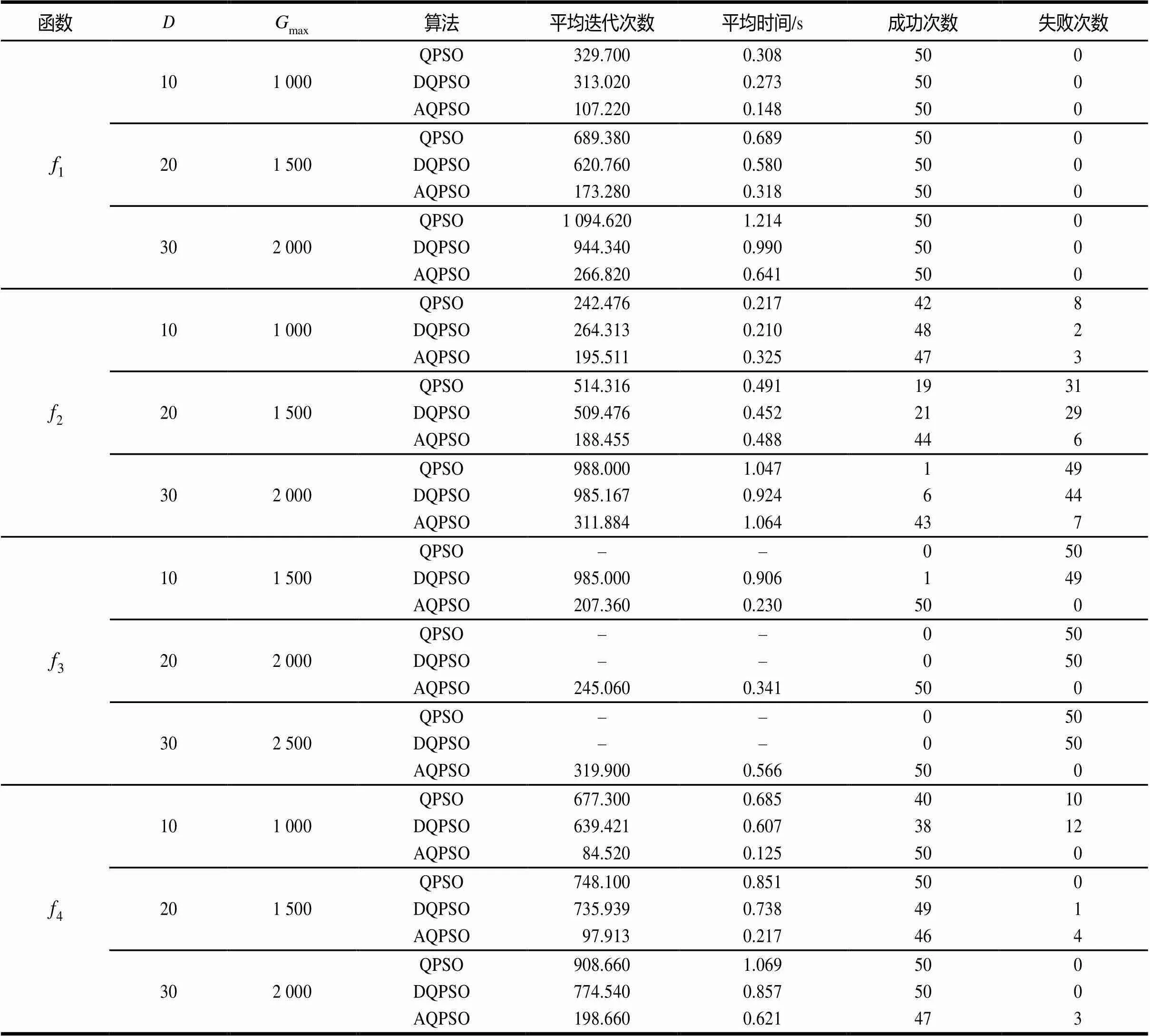
表3 固定精度的仿真结果
5 结束语
在本文提出的AQPSO算法中,自适应收缩-扩张系数有助于粒子跳出局部最优位置,提高全局搜索能力;双中心协作思想有助于粒子更充分地利用群体信息,改进全局最优位置的更新方式,提高全局最优位置的指引作用。上述2个创新点的结合,可有效提高算法的寻优能力,加快收敛速度。实验结果证明,AQPSO在寻优能力和寻优速度上均取得了较好的效果。下一步将设计性能更优的自适应收缩-扩张系数方法,以提高全局搜索能力,同时利用群体知识提高群体学习能力,从而进一步提高算法的寻优能力。
[1] Sun Jun, Feng Bin, Xu Wenbo. Particle Swarm Optimization with Particles Having Quantum Behavior[C]//Proc. of 2004 Congress on Evolutionary Computation. Piscataway, USA: [s. n.], 2004.
[2] Sun Jun, Xu Wenbo, Feng Bin. A Global Search Strategy of Quantum-behaved Particle Swarm Optimization[C]//Proc. of IEEE Conference on Cybernetics and Intelligent Systems. Singapore: IEEE Press, 2004.
[3] 李盼池, 王海英. 量子势阱粒子群优化算法的改进研究[J]. 物理学报, 2012, 61(6): 19-27.
[4] 方 伟, 孙 俊, 谢振平, 等. 量子粒子群优化算法的收敛性分析及控制参数研究[J]. 物理学报, 2010, 59(6): 3686- 3694.
[5] 黄泽霞, 俞攸红. 惯性权自适应调整的量子粒子群算法[J].上海交通大学学报, 2012, 46(2): 228-232.
[6] 程 伟, 陈森发. 权重自适应调整的混沌量子粒子群优 化[J]. 计算机工程与应用, 2010, 46(9): 46-48.
[7] Gong Shangfu, Gong Xingyu, Bi Xiaoru. Feature Selection Method for Network Intrusion Based on GQPSO Attribute Reduction[C]//Proc. of International Conference on Multimedia Technology. Hangzhou, China: [s. n.], 2011.
[8] Lu Kezhong, Fang Kangnian, Xie Guangqian. A Hybrid Quantum-behaved Particle Swarm Optimization Algorithm for Clustering Analysis[C]//Proc. of the 5th International Conference on Fuzzy Systems and Knowledge Discovery. Jinan, China: [s. n.], 2008.
[9] 胡苓苓, 郭业才. 基于QPSO的小波分数间隔盲均衡算 法[J]. 计算机工程, 2011, 37(24): 195-197.
[10] 汤可宗, 柳炳祥. 双中心粒子优化算法[J]. 计算机研究与发展, 2012, 49(5): 1086-1094.
[11] Li Yangyang, Xiang Ronggong, Jiao Licheng. An Improved Cooperative Quantum-behaved Particle Swarm Optimization [J]. Soft Computing, 2012, 16(6): 1061-1069.
[12] Kennedy J, Eberhart R. Particle Swarm Optimization[C]//Proc. of IEEE International Conference on Neural Networks. Piscataway, USA: IEEE Press, 1995.
[13] Sun Jun, Fang Wei, Wu Xiaojun. Quantum-behaved Particle Swarm Optimization: Analysis of the Individual Particle’s Behavior and Parameter Selection[J]. Evolutionary Compu- tation, 2012, 20(3): 349-393.
[14] Zhu Haodong, Zhong Yong. Study of Optimized RBF Network in Feature Selection[J]. Journal of Microcomputer & Its Applications, 2009, 28(15): 76-79.
[15] Liu Junhui, Li Na. Parallel Adaptive Immune Quantum-Behaved Particle Swarm Optimization Algorithm(PAIQPSO)[C]//Proc. of International Conference on Intelligent Systems Design and Engineering Application. Sanya, China: [s. n.], 2012.
[16] 陈 伟, 周 頔, 孙俊陈, 等. 一种采用完全学习策略的量子行为粒子群优化算法[J]. 控制与决策, 2012, 27(5): 719- 730.
编辑 金胡考
Cooperative Double-center QPSO Algorithm with Self-adaptive Contraction-expansion Coefficient
DING Yinga, LI Feib
(a. College of Communication & Information Engineering; b. Institute of Signal Processing and Transmission, Nanjing University of Posts and Telecommunications, Nanjing 210003, China)
Against the problems of Quantum Particle Swarm Optimization(QPSO) algorithm in the late part of iterations, such as decline of population diversity, slow convergence rate and easy to fall into the local optima, a cooperative double-center QPSO algorithm with self-adaptive contraction-expansion coefficient is proposed in this paper. It has two characteristics: (1)The contraction-expansion coefficient is self-adaptively adjusted, which can help jump out of the local optima and improve the global search ability; (2)It renews the global best location of every iteration in two ways, and one way of them is the same as that in QPSO, the other is that double-center particles, together with the current global optimal location, which is used to improve the way of renewing the global best location by cooperating in the corresponding dimensions among them. The performance of this algorithm is analyzed from fixed iterations and fixedprecisions. Experimental results show that compared with QPSO, it has higher convergence rate and better search ability.
Quantum Particle Swarm Optimization(QPSO) algorithm; contraction-expansion coefficient; double-center particle; cooperative; global optimal location
1000-3428(2014)03-0232-06
A
TP301.6
丁 颖(1988-),女,硕士研究生,主研方向:量子信息技术;李 飞,教授
2013-01-23
2013-03-05 E-mail:dingying_better@163.com
10.3969/j.issn.1000-3428.2014.03.049

