工业控制系统信息安全风险评估量化研究
卢慧康 陈冬青 彭 勇 王华忠
(华东理工大学信息科学与工程学院1,上海 200237,中国信息安全测评中心2,北京 100085)
0 引言
工业控制系统(industrial control system,ICS)广泛应用于石油化工、交通运输、水处理等国家关键基础设施中[1]。随着信息技术的发展以及“两化”融合的深入,传统的工业控制系统与IT系统,甚至与Internet连接越来越紧密,导致ICS面临的安全威胁不断增多。近年来,ICS领域的信息安全事件频发。2010年一个名为“震网”的病毒攻击了伊朗的布什尔核电站,导致离心机大量损坏,严重打击了伊朗的核计划[2]。层出不穷的控制系统信息安全事件表明,加强ICS的保护已经变得迫在眉睫。
风险的量化评估是ICS信息安全研究的重要基础。国外ICS信息安全风险评估起步较早,已建立了如NIST800-82、ISA/IEC 62443等的国际标准和指南[3-4];而国内在该领域的研究尚处于探索阶段。目前,国内外还没有一套行之有效的针对ICS信息安全风险量化评估方法。本文针对 ICS的特点,以NIST800-82和IEC 62443为依据,进行了风险分析,提出了基于模糊层次分析法(analytic hierarchy process,AHP)的ICS信息安全风险评估方法。经过实例论证,该方法行之有效,可以为工业控制领域信息安全风险评估工作提供借鉴。
1 信息安全风险分析
全面的风险分析是开展风险评估的前提。ICS有区别于传统IT系统的特点,如ICS不能容忍延迟和无计划的中断发生,任何复杂的数据加密认证产生的延迟都可能会造成系统故障,由于ICS的逻辑执行会直接影响物理世界,设备出现故障后可能造成有毒原料泄漏、区域停电等大规模不可预知的影响[5]。ICS的现实特点表明其对实时性和稳定性要求非常高。因此,在确保系统满足信息安全需求的同时,应尽量避免所部署的安全设备对工艺过程的稳定性和实时性造成影响。
风险分析分别从满足信息安全需求和工艺需求两个方面对资产进行识别,形成资产类要素;根据资产脆弱点的严重程度识别系统脆弱性要素;再对ICS面临的威胁要素和已部署的安全措施类要素进行全面的识别,最终建立风险评估模型。通过分析各要素之间的关联程度,计算出系统的风险值。风险分析模型如图1所示。

图1 风险分析模型图Fig.1 Risk analysis model
1.1 资产识别
资产的价值属性是其风险存在的根源。ICS资产存在的形式多种多样,按照资产不同的存在形式,可归为4大类:硬件资产、软件资产、人力资源、专利商誉。
从满足工艺需求和满足安全需求两个方面对资产进行识别。如满足工艺需求的硬件资产主要有远程终端装置(remote terminal unit,RTU)、可编程逻辑控制器(programmable logic controller,PLC)、SCADA 服务器或主终端单元(main terminal unit,MTU)、智能电子设备(intelligent electronic devices ,IED)、输入/输出(I/O)服务器、现场总线系统等。满足安全需求的硬件资产包括主机、交换机、路由器、网关、防火墙等。满足工艺需求的软件资产主要有组态监控软件、工控编程软件等。满足安全需求的软件资产主要是指通信软件、互联网应用软件、办公软件、防病毒软件等。
1.2 威胁识别
工业控制系统遭受的威胁日益严峻。关键基础设施的安全是国家经济稳定运行的关键,因此也成为了敌对政府、商业间谍、恐怖组织等外部恶意入侵者进行信息战的重要战场[6]。系统内部有意的人为事故、无意的操作失误和设备故障等也会对ICS造成破坏。例如,一些组织内部存在移动存储介质混用、随意安装各类软件、访问未经授权网站等行为,这类行为不仅影响工作效率,造成操作失误,更为病毒、木马等恶意代码侵入系统留下隐患。本文按照威胁的来源进行分类,将威胁细分为5类:自然环境威胁、内部无意威胁、内部有意威胁、外部攻击和第三方威胁。
1.3 脆弱性识别
脆弱性的识别是风险评估中最重要的一个环节。ICS的脆弱性总体上可分为技术和管理两个方面。一直以来,ICS的设计部署主要满足系统的实时性和稳定性,忽略了信息安全要求,这使得系统本身在平台、网络等技术层面存在脆弱性。同时,组织内部信息安全管理措施严重缺乏,如安全防范制度不完善,安全设备的操作流程不明确,无定期、有效的系统风险检查措施,人员的信息安全意识淡薄,应急培训落后等。
1.4 安全措施识别
威胁能够利用脆弱性对资产进行攻击,部署安全措施目的是降低威胁事件发生的概率和产生的影响,从而降低系统的风险。而不适当的安全措施本身就存在可以被利用的脆弱性。因此,在风险分析的过程中,必须对其已经部署的安全控制措施的有效性进行全面的检查评估。ICS常采取的安全控制措施主要有[7]:制定相关法律法规、工作程序和工作指南;建立合理的组织架构、配备相关人员;采取合理有效的技术措施等。
一般来说,单一的安全措施所发挥的防范作用是有限的,其部署具有集合性,即某一类有效的安全措施的集合。如图2所示,根据安全措施的部署的集合性和所发挥的作用分为:预防性安全措施、检测性安全措施以及补救性安全措施。

图2 工业控制系统的安全措施Fig.2 Security measures for industrial control system
2 信息安全风险评估
2.1 层次分析法
层次分析法(AHP)最早是由美国匹兹堡大学教授萨蒂于20世纪70年代提出,后在风险评估领域广泛应用[8]。它是一种定性分析和定量分析相结合的多层次权重决策分析方法,其核心思想是对复杂决策问题的本质、影响要素以及内在关系进行深入分析,建立层次结构模型,构造两两比较判断矩阵,计算各要素的权值并按其重要性进行排序。
层析分析法的研究热点[9-10]主要集中在判断矩阵的构造和调整、排序权值的合理计算和判断矩阵的一致性检验问题。常用的计算判断矩阵排序权值的方法有:①和积法;②列和求逆法;③行和正规化法;④特征值法。其中,前3种方法只考虑判断矩阵单一行列的影响,计算精度不高,常作为迭代初值。特征值法运用范围较广,但没有考虑到判断矩阵一致性条件,所以当判断矩阵的一致性很差时,求解特征值就很困难,需要反复地调整、检验[11]。同时,专家在对风险各要素两两比较的定性评价中采用极端的判断,没有体现客观世界各要素之间普遍存在的不确定性和模糊性。
2.2 模糊层次分析法
针对前述问题,本文对传统层次分析法进行了改进,引入模糊数学概念,与层次分析法相结合,形成模糊层次分析法。该方法采用专家模糊评判的方式构造模糊互补矩阵,并对矩阵进行一致化处理,构造模糊一致判断矩阵,对各要素的相对重要性进行排序。该方法解决了判断矩阵的一致性问题。
2.2.1 模糊一致判断矩阵
定义1 若模糊矩阵R=(rij)n×n满足条件rij+rji=1,i,j=1,2,…,n,则称模糊矩阵 R 为模糊互补判断矩阵。
定义2 若模糊互补矩阵R=(rij)n×n满足条件rij=rik- rjk+0.5,i,j,k=1,2,…,n,则称 R 为模糊一致判断矩阵。
专家的模糊判断所构造的判断矩阵是模糊互补判断矩阵 R=(rij)n×n,对模糊互补判断矩阵 R=(rij)n×n按行求和记为ri。按公式,对其实施数学变换,由此建立模糊一致判断矩阵RM=(fij)n×n。
在模糊一致判断矩阵中,fij是元素i与j相对重要性的度量,且fij越大,元素i比j越重要。矩阵优先关系数量标度如表1所示。

表1 矩阵优先关系数量标度方法Tab.1 Quantitative scaling methods of matrix precedence relation
为得到各风险因素的相对权重,对建立的模糊一致判断矩阵RM=(fij)n×n计算排序:

2.2.2 风险评估步骤
①建立风险层次结构模型
在深入分析ICS信息安全风险各要素的基础上,建立基于资产、脆弱性、威胁和已部署的安全措施的风险评估模型。模型分为3层,目标层ICS风险;准则层资产、脆弱性、威胁和安全措施;因素层是风险分析过程中识别的影响各指标的风险因素。同层各因素对上层因素产生影响,同时受到下层的作用。工业控制系统风险层次结构模型如图3所示。

图3 工业控制系统风险层次结构模型Fig.3 Risk hierarchy model of industrial control system
②划分因素集X
影响ICS信息安全风险的因素X构成因素集合F={A1,A2,…,Ai},i=1,2,…,n。对因素集中每个风险因素 Ai进行划分,即 Ai={Ai1,Ai2,…,Aik},其中 i,k=1,2,…,n。
③单因素模糊评判
对每个因素Ai的多个风险因素,作单因素综合评判。构造Ai的若干因素总的模糊互补矩阵为Ri,按公式转换成模糊一致矩阵 RMi,计算Ai中各指标重要程度的子集为Wi。根据专家模糊评价,得到单因素模糊评判矩阵RAi。根据式(2)求出单因素评判结果Bi。

④多因素模糊综合评判
因素集F={A1,A2,…Ai}的各因素重要程度模糊集合为 W={W1,W2,…,Wn},则 X 总的模糊综合评价矩阵R为:

根据公式B=WR求得多因素综合评判结果B。
⑤综合评判结果反模糊化
利用模糊综合评判所得到的评价结果B同样是一个模糊向量。为使系统风险的评价结果更为明朗,还需对模糊向量进行精确化(又称反模糊化)。反模糊化方法有很多,如最大隶属度法、最大平均法、重心法、中位数法等。最大隶属度方法的应用较为广泛[14],即模糊集合中隶属度最大的等级作为最终等级,但当模糊向量B各分量相差不大时,结果很不准确。本文运用重心法对评价结果B=(b1,b2,…,bi)进行反模糊化处理,得出风险的最终值B*,其计算公式如式(4)所示。

3 实例论证
针对上海某石化企业水处理控制系统进行风险评估,其网络拓扑图如图4所示,整个控制系统使用以太网通信。对该工业控制系统的安全风险按照资产A1、脆弱性A2、威胁A3和已采取的安全措施A4四个方面建立如图3所示的机构模型。该系统的关键硬件资产有总交换机、现场交换机、操作员站、工程师站以及底层的控制单元(RTU/PLC)。现场交换机采用光纤传输的方式将现场控制设备采集的数据汇总到总交换机,并上传至操作站。
企业邀请了由工控领域专家、石化企业高级工程师、信息安全领域有关专家组成的决策专家组(共10人),对工业控制系统安全风险的各风险因素进行赋值,如对“资产 A1”涉及的4类风险因素硬件资产A11、软件资产 A12、人力资源 A13和专利和商誉A14的相对重要性予以判断赋值,并由此构造模糊判断矩阵 R1。

图4 DCS控制系统网络拓扑图Fig.4 Network topology of DCS
构造的模糊判断矩阵R1如式(5)所示。


为得到风险因素的相对权重,通过式(1)对建立的模糊一致矩阵RM1进行排序,取,各相对权重之间的差异最大。当i=1时,得到“硬件资产”的权重值w1为:

分别计算当i=2、3、4时wi的值。由此得出“资产A1”中各要素的相对权重为:
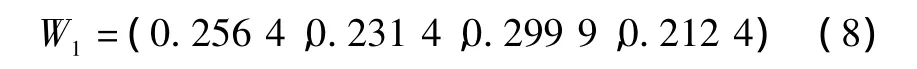
同理,求得A2、A3、A4的权重分别如下:

综上可得水处理控制系统信息安全风险各风险要素相对权重集:

对于给定的工业控制系统,单因素评价可再次邀请专家来进行。将资产的价值重要性分为5级,集合表示为{很低,低,中,高,很高}。例如,以“资产 A1”中“硬件资产A11”因素为例。若有0%人员认为硬件资产在资产中的重要程度很低,0%的人员认为重要性低,30%的人员认为重要性中等,30%的人员认为重要性高,40%的人员认为硬件资产在系统资产中具有很高的重要性,于是有关“硬件资产A11”因素的评价关系是(0,0,0.3,0.3,0.4)。同理可得“资产 A1”中其他资产类型的关系。
确定单因素模糊评判矩阵RA1如下:

由式(2)计算得出资产因素A1的单因素评价结果BA1如下所示:

同理,依次进行脆弱性A2、威胁A3和安全措施A4的单因素评判,得到评判结果如下:

最后根据公式B=WR求得模糊综合评判结果B:

建立风险的评语集并赋值:B={安全,风险低,风险中,风险高,风险很高}={1,2,3,4,5}。由式(3)得到系统最终风险等级B*=3.165。因此,该水处理控制系统的信息安全风险为中,需提高安全防护等级与安全管理水平。
4 结束语
本文针对工控系统信息安全风险评估问题,结合传统IT系统信息安全风险评估理论与工控系统特点,提出了基于模糊AHP的工业控制系统信息安全风险评估方法,以克服传统AHP评估方法的不足。通过邀请专家组对风险指标权重进行模糊评价,构建模糊一致判断矩阵,确定层次结构中各指标的权重系数,自下而上对工业控制系统进行模糊综合评判。通过重心法对模糊综合评判结果反模糊化,得到工控系统信息安全风险的量化值。运用该方法进行实例评估,证明其行之有效。但该方法在确定指标权重时仍然存在受主观不确定性的影响,如何解决这一问题是未来研究的重点之一。
[1]ANSI.Std.99.00.01 Security for industrial automation and control systems part 1[S].ISA,2007.
[2]Valenzano A,Durante L,Cheminod M.Review of security issues in industrialnetworks[J].IEEE Transactions on Industrial Informatics,2013,9(1):277 -293.
[3]Stouffer K,Falco J,Scarfon K E.Guide to industrial control systems(ICS)security[S].NIST Special Publication,2008.
[4]ISA99.IEC 62443 Industrial control network & system security standardization[S].ISA,2011.
[5]彭杰,刘力.工业控制系统信息安全性分析[J].自动化仪表,2012,33(12):36 -39.
[6]Kang D J,Lee J J,Kim S J,et al.Analysis on cyber threats to SCADA systems[C]∥IEEE Transmission & Distribution Conference& Exposition,2009:1 -4.
[7]Ralston P A S,Graham J H,Hieb J L.Cyber security risk assessment for SCADA and DCS networks[J].ISA Transactions,2007,46(4):583 -594.
[8]Tolga E,Demircan M,Kahraman C.Operating system selection using fuzzy replacement analysis and analytic hierarchy process[J].International Journal of Production Economics,2005,97(1):89 -117.
[9]Saaty T L.Analytic hierarchy process[J].Encyclopedia of Biostatistics,2005.
[10]李春好,孙永河,贾艳辉,等.变权层次分析法[J].系统工程理论与实践,2010,30(4):723 -731.
[11]岳瑞华,王学浩,徐中英.自动测试系统性能的模糊综合评价方法研究[J].自动化仪表,2011,32(11):69 -71.
[12]张吉军.模糊一致判断矩阵3种排序方法的比较研究[J].系统工程与电子技术,2003,25(11):1370 -1372.
[13]吕跃进.基于模糊一致矩阵的模糊层次分析法的排序[J].模糊系统与数学,2002,16(2):79 -85.
[14]肖龙,戚溺,李千目.基于AHP和模糊综合评判的信息安全风险评估[J].计算机工程与应用,2009,45(22):82 -85.

