二维数控精密转台精度计算与分析
(长春理工大学 机电工程学院,吉林 长春 130022)
二维数控精密转台精度计算与分析
周锐琦 史国权 胡明亮
(长春理工大学 机电工程学院,吉林 长春 130022)
根据二维转鼓的生产要求和提出的技术指标,对二维数控精密转台进行了精度计算和分析。介绍了对转台精度起主要影响作用的各项误差,得到二维数控精密转台的指向误差,并对指向误差进行分配,得出二维数控精密转台三类误差指标。
二维数控;转台精度;指向误差
1 概述
针对非规则(二维)光学转鼓在扫描探测器中的广泛应用和产量需求,自主研发能够和Ultraform250超精密切削机床配套使用的二维数控精密转台夹具。
由于二维数控精密转台是针对非规则光学转鼓的高效、高质量飞切加工的,在加工过程中,产生加工误差的因素很多。如果对转鼓规定一系列技术指标,那么转台的有关误差对转鼓的技术指标的影响是很大的。因此,要尽可能设法减少这些误差,所占的比重越大,留给补偿其他各类误差的空间就越小。其结果不是降低零件的加工精度,就是增加加工难度。根据所生产转鼓的技术指标:平行度误差15角秒,倾角误差20角秒,转角误差20角秒,对转台结构的精度进行逆推,经过计算得出转台各主要误差指标。
2 转台的系统误差
由于转台的结构是二维数控工艺装置夹具结构,对静态条件下的转台性能指标要求比较高,下面对转台精度起主要影响作用的各项误差给出定义 :
回转误差是指各轴在进行转动时,轴端的运动轨迹所形成的包络线摆动范围的最小圆锥角度。它能够直接影响轴的空间指向。
垂直度误差是指转台空间直角坐标系中两轴轴线之间的实际空间夹角与90°角的差值。
位置误差是指在静止状态下,转台的实际位置和理想位置的差值。
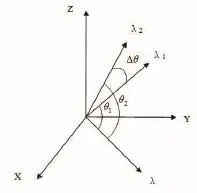
图1 二维数控精密转台指向误差示意图
3 二维数控精密转台的指向误差
3.1 指向误差的定义(见图1)
转台的指向误差指的是在横滚轴上确定一个单位向量λ0,当转台转动一定的角度后,转台的理想指向λ1与实际指向λ2之间的角度偏差指向误差实际上是一种空间角度误差,能够直接反应出转台的定位精度。在三维空间坐标中的单位向量的指向误差如图1所示。
指向误差的空间几何意义可以这样描述:设与横滚轴轴线重合的一个单位向量λ0,按照欧拉变换的顺序,将横滚轴和方位轴依次旋转一定角度,则单位向量λ0回转到一个新的位置,在新的方向上得到新的单位向量λ1,则有:
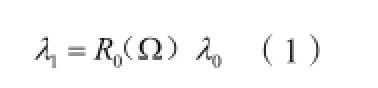
式中,R0(Ω)为欧拉变换矩阵。
可是,二维数控精密转台在做回转运动时,会存在一系列的误差E,这会导致单位向量λ0经过两轴回转后,达不到预期的位置,也就得不到新的单位向量λ1,而是得到了单位向量λ2,正因为这些误差的存在,可推出公式:
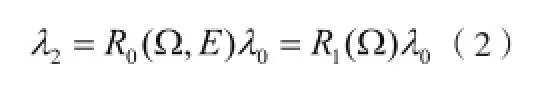
这里误差E代表各个误差,它主要由三类误差组成:轴之间的垂直度误差
α,轴的回转误差β,以及轴的位置误差γ,则有:
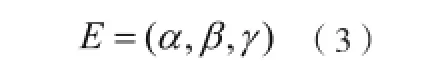
那么指向误差则可表示为由单位向量λ1和单位向量λ2两个向量差的模长△Φ:
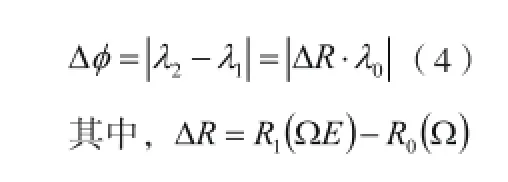
3.2 指向误差的算法
下面通过矩阵形式,把指向误差的公式求解出来。
转台两轴依次绕X,Z轴转动X1,X2角度,在没有误差的情况下,单位向量λ0将变成λ1:λ1= R0(Ω)λ0,其中
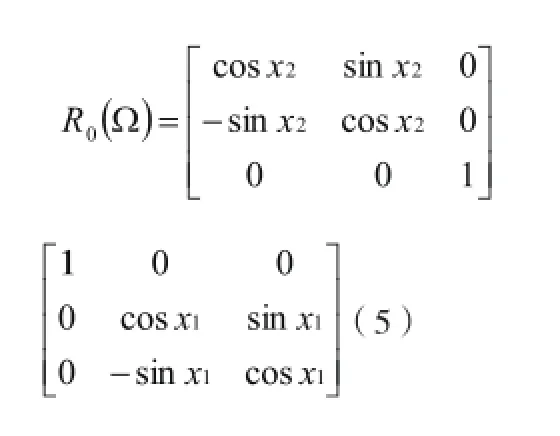
由于存在误差因素E,单位向量λ0会变成λ2。设垂直度误差α1;回转误差β1, β2;位置误差γ1,γ2。在转动两轴时,根据轴的三类误差,得到指向转换所产生的中间变量的欧拉变换矩阵:
X轴转动X1角度时,产生位置误差γ1和回转误差β1:
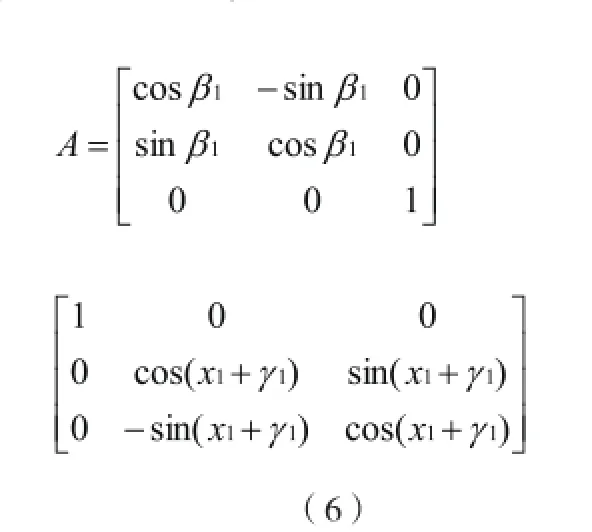
Z轴转动x2角度时,产生位置误差γ2和回转误差β2:
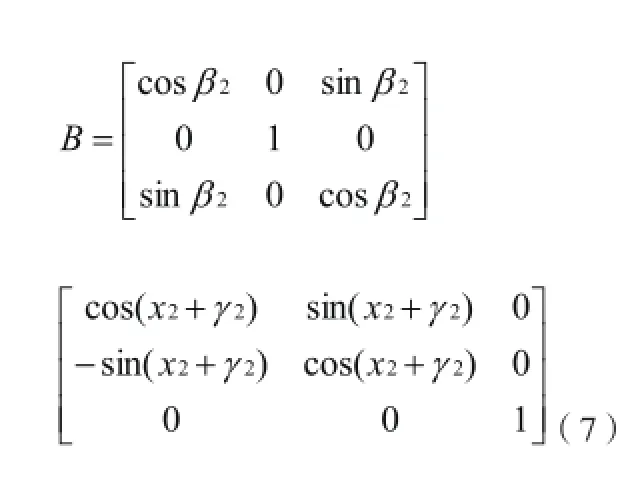
两轴之间垂直度误差α1:

于是,得到含有三类误差的变换矩阵为
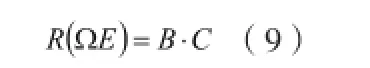
进而可以用公式(4),求出指向误差△Φ。
4 转台的指向误差分配
由于指向误差受正交性误差α,回转误差β和定位误差γ三类误差的影响,但三类误差对指向误差的影响程度不同。所以要对指向误差进行分配。
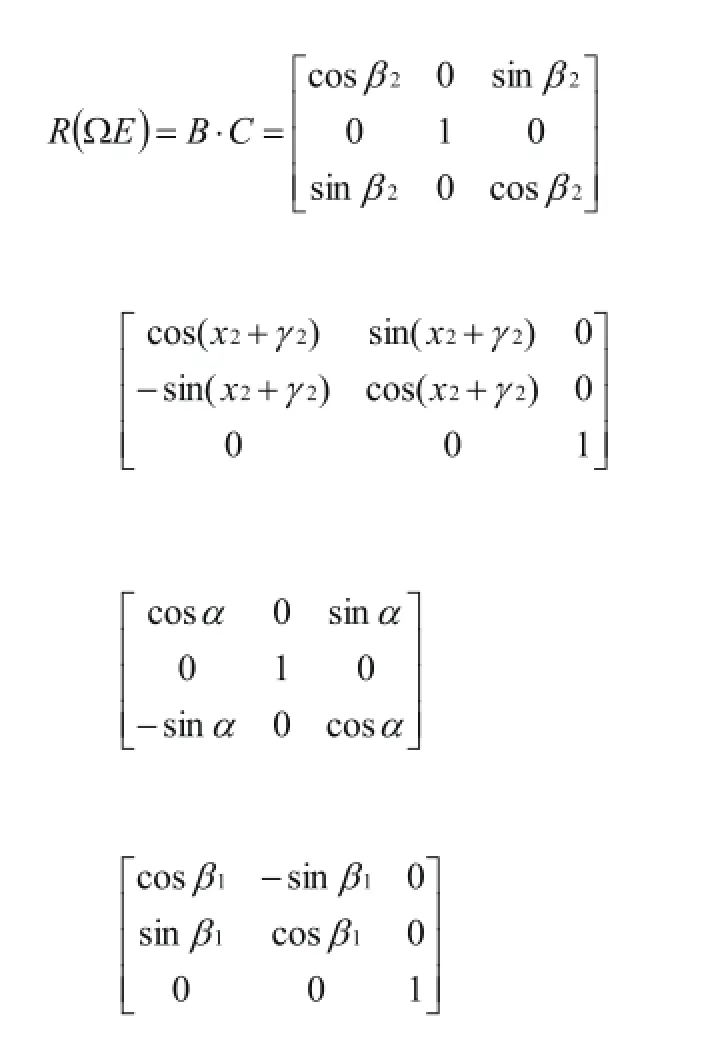
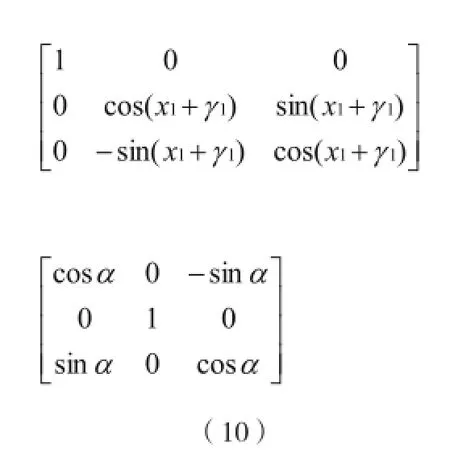
根据控制变量法,可计算出三类误差对指向误差的影响程度。当垂直度误差变化时,分别取值0″,1″,2″,3″,4″,5″得到各自的实际指向,再计算相邻两个实际指向的余弦值,从而得到相邻两个实际指向的夹角。
根据公式:
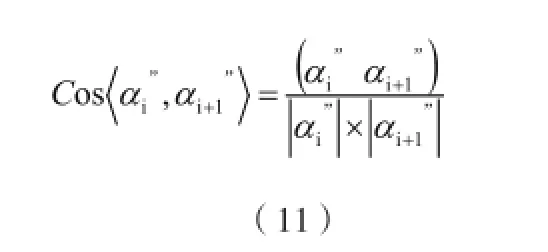
得到相邻两个实际指向的夹角:
<0″,1″>=0.9999″;
<1″,2″>=0.9999″;
<2″,3″>=1.1339″;
<3″,4″>=0.8720″;
<4″,5″>=0.9999″
同理,当回转误差和定位误差变化时,利用同样的方法,观察实际指向的变化情况。则计算得出以下结论:
回转误差每增加1角秒,指向误差大约增加1.4角秒;而垂直度误差和定位误差每增加1角秒,指向误差均大约增加1角秒左右。
根据三类误差对指向误差的影响,采用加权方法对三类误差进行误差分配,设
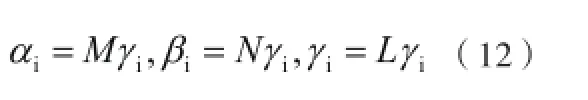
其中,M、N、L为加权系数。
为了让产生指向误差的三类误差对指向误差的影响具有相同的程度,则可确定加权系数为M=1,N=0.71,L=1。
由于三类误差均对转角误差、倾角误差有影响,那么就可以把加权系数代入,从而计算出三类误差。因为要保证转鼓相邻的两个加工面的转角误差不大于20角秒,需要把各个面的加工误差控制在10角秒以内。计算得到横滚轴和方位轴的三类误差指标分别为:回转误差2.6角秒,定位误差3.7角秒,垂直度误差3.7角秒。同样,方位轴在转动过程中,也要保证每次回转时产生的倾角误差在10角秒以内,则前面计算得到的三类误差满足要求。根据加工转鼓的加工工序可知道,加工完一个面后,需要转动横滚轴180°,所以影响转鼓平行度误差的是横滚轴的回转误差和定位误差。由于横滚轴每次转动时产生的误差要控制在7.5角秒以内,而前面计算出来的回转误差和定位误差之和小于这一数值,则满足转鼓的加工要求。
结语
本文通过对二维数控精密转台的精度计算和分析,确定了对转台精度起主要影响作用的三类误差指标。计算结果表明:三类误差对指向误差的影响程度不同。根据这一结论,对误差进行分配。本文的结论可作为转台精度的技术要求,为转台的设计提供依据,因此对转台的制造具有重要的指导意义。
[1]张文涛.金刚石飞切二维转鼓加工精密转台定位精度分析.新技术新工艺,2011,11∶40-42
[2]白雪峰.单轴速率三轴位置惯性测试转台误差及传递分析.航天控制,2006,24(02)∶26-29
[3]Louis A DeMore.Design Study for a High-Accuracy Three-Axis Test Table.AIAA Guidance and Control Conference,1985,10(01)∶104-114
[4]周锐等.飞行仿真转台指向误差分析及误差分配.航天控制.1996,14(03)∶66-72
[5]曲智勇.仿真转台误差分析及误差建模.计算机仿真,2006,23(03)∶301-303
V216 < class="emphasis_bold"> 文献标识码:A
A

