基于可Markov分割混沌系统的图像加密算法

刘 泉 李佩玥 章明朝 隋永新 杨怀江



基于可Markov分割混沌系统的图像加密算法

刘 泉*①②李佩玥①章明朝①隋永新①杨怀江①

①(中国科学院长春光学精密机械与物理研究所应用光学国家重点实验室 长春 130033)②(中国科学院大学 北京 100039)

为了设计复杂度高、安全性好而计算代价小的图像密码算法，该文从一类新的具有Markov分割性质的混沌系统出发构造了此算法。首先，通过控制此混沌系统的参数并配合时空混沌系统设计了一个密钥流发生器；然后，利用真随机数发生器产生的随机数来扰动系统的初始密钥，以动态生成图像的置换矩阵和加密密钥流；最后，通过利用不同群中的加法混合运算构造扩散函数以增加破译复杂度，以两轮迭代完成了图像加密过程。实验结果表明，此混沌系统产生的密钥流序列有比较好的统计特征，该算法可以破坏原始图像的特征，使得密文图像难以辨识。进一步分析可知，该算法可以很好地抵抗差分分析等其它已知攻击，效率高于一些基于超混沌系统设计的密码算法。此外，此算法计算简单，安全性高，易于实现，具有良好的应用前景。

图像加密；混沌；Markov分割；时空混沌

1 引言

近年来，网络上保存和传输的图像数据量越来越大，图像信息的保密性成为一个突出问题，而加密算法可以保证仅授权用户才能获知图像信息，从而实现对图像信息的保密。传统的加密算法如数据加密标准DES、高级加密标准AES、国际数据加密算法IDEA等是基于文本设计的，将其用在图像加密上并不合适[1,2]，主要是因为AES等加密算法加密后的图像，其图像信息依然可以感知，这是由图像信息不同于文本信息，其相邻像素存在很强的相关性所致。

基于上述分析，本文采用了一类新的混沌系统[13]，该系统是一类具有Markov性质的分段线性映射。可以证明它产生的序列服从均匀分布，线性不相关，没有不动点，这比基于Logistic映射设计的混沌密码算法要好，通过参数的选取，它可以避免类似Tent映射的有限精度退化问题。文献[14]指出，Logistic映射和Tent映射复杂度低，不适合用于设计密码算法，而本文所用混沌系统[13]是一种新型低维混沌系统，通过参数选取，产生的复杂度比Logistic和Tent映射大得多，这意味着其更接近真随机数[15]，显示其实用价值。为解决低维混沌系统密钥空间小的问题，采用时空混沌系统是一种不错的选择[16]，本文利用上述新的混沌改进了耦合格子映射，其产生的序列具有更好的统计性质。利用产生的序列构造置换矩阵，并用它来构造扩散阶段的密钥序列。通过对算法置乱和扩散阶段的函数进行优化，采用不同群中的加法混合运算构造的扩散函数可以更好地抵抗CPA和CCA攻击。本文设计的算法迭代两轮即可产生比较好的加密效果，而加解密效率并不低。

本文组织如下：第2节给出本文所用的混沌系统及其性质说明；第3节介绍本文所用的图像加密算法；第4节给出所用系统的各种测试；最后是本文内容的总结。

2 混沌系统构造

2.1 可Markov分割的混沌系统的特性

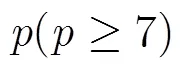
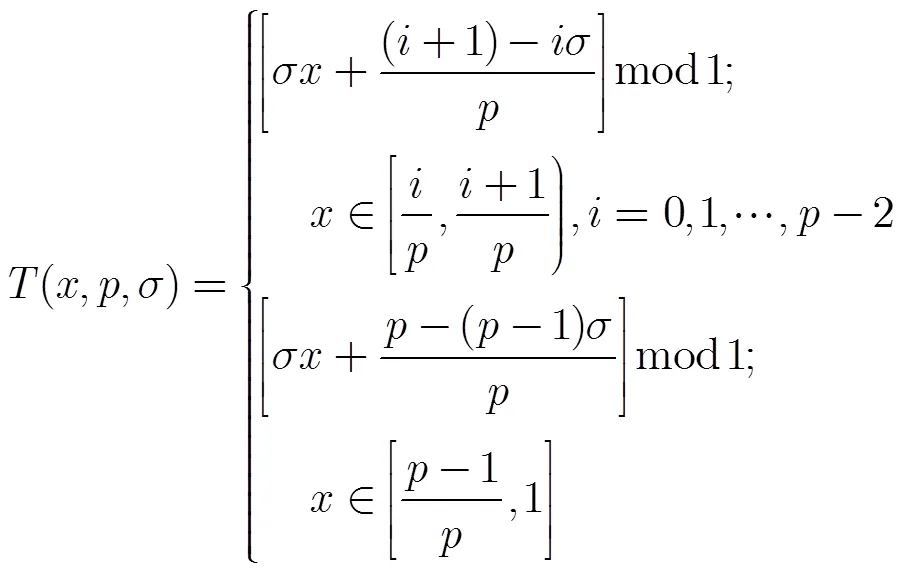
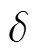
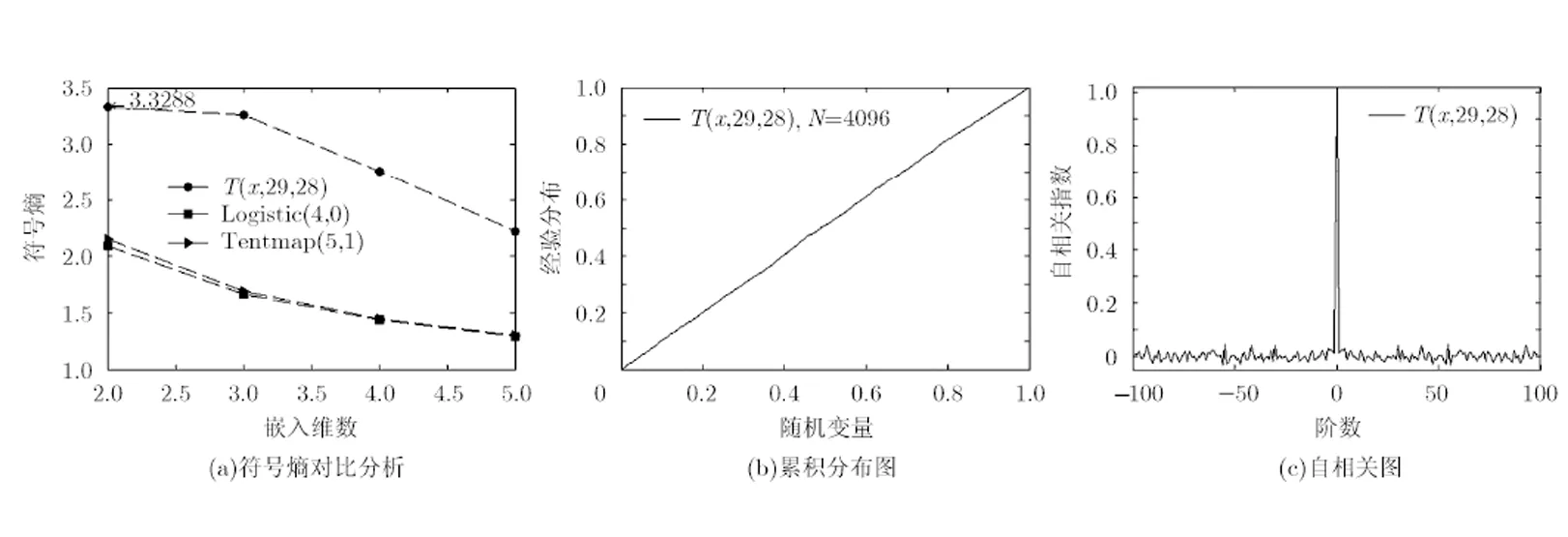
图1 序列的基本统计性质

2.2 改进时空混沌系统

低维的混沌系统因密钥空间限制和相空间结构简单而可能产生安全漏洞，这可以利用时空混沌系统来解决，其中最常用的是耦合格子映射。一个阶的单向发展的耦合格子映射如式(2)，可掩盖系统的相空间结构，其常用于密码系统的设计，其结构表示如式(2)。

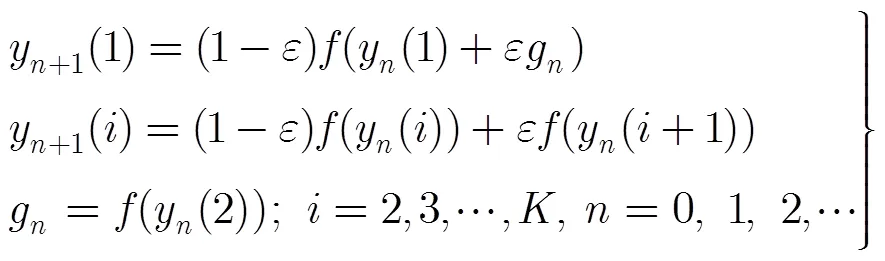
3 图像密码算法构造

3.1 算法框架

分析了上述加耦合格子映射的混沌系统性质后，利用其产生的序列生成密钥流，根据密钥流生成动态置乱矩阵，对图像像素位置进行置乱，然后利用迭代加密模块对像素数值进行替换。该图像密码算法分为3个部分：密钥生成算法，加密算法和解密算法。其加密过程如图3所示。

3.2 密钥流生成算法

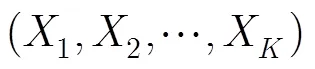
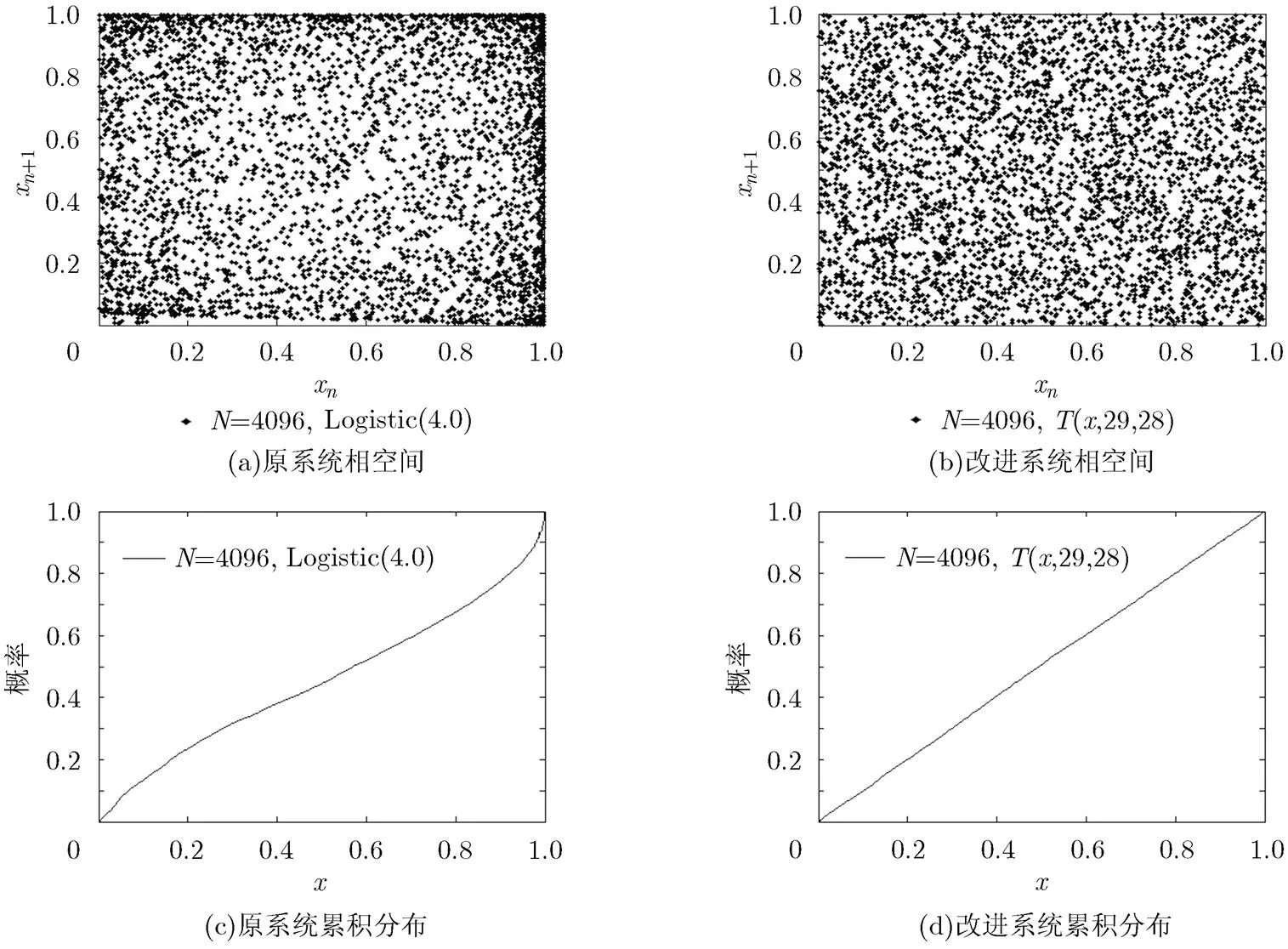
图2 改进的时空混沌与原系统的特性对比

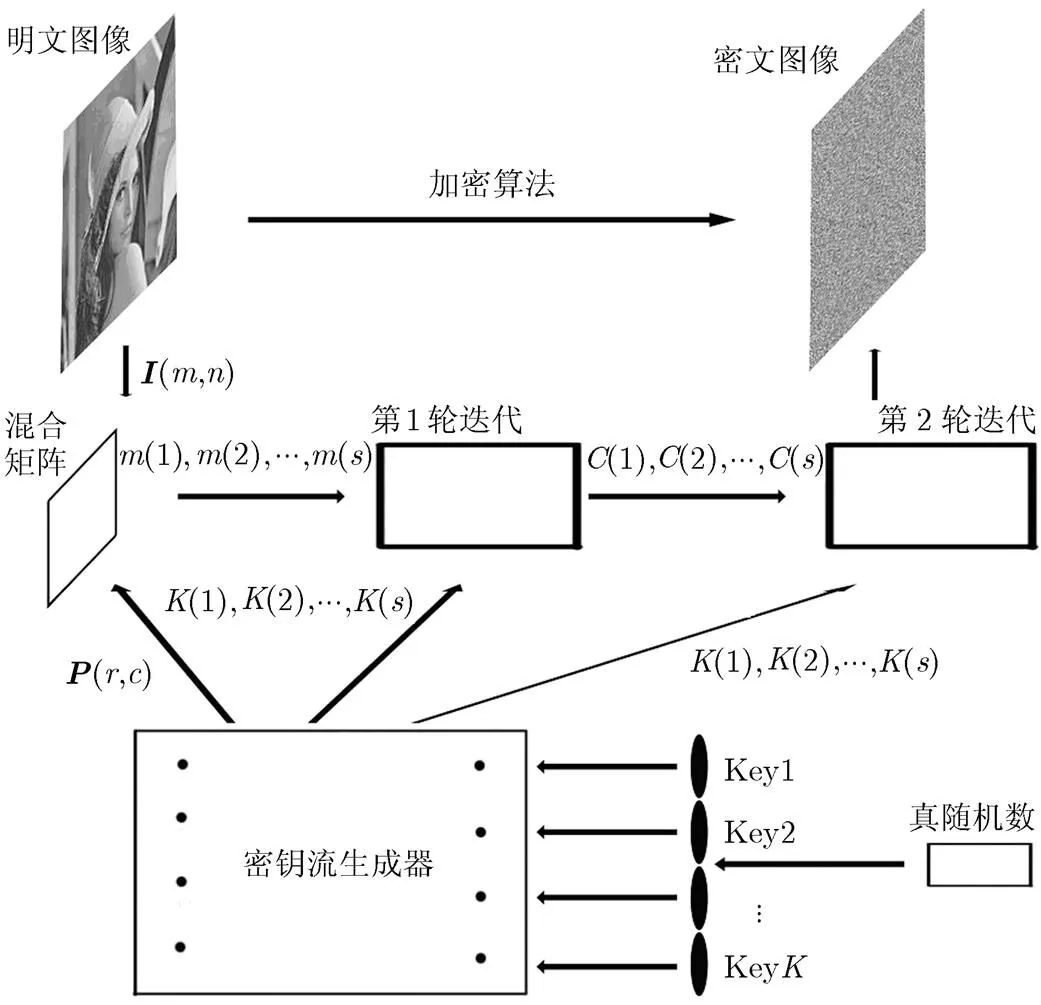
图3 图像加密算法框架

3.3 加密步骤

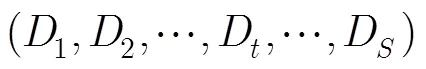
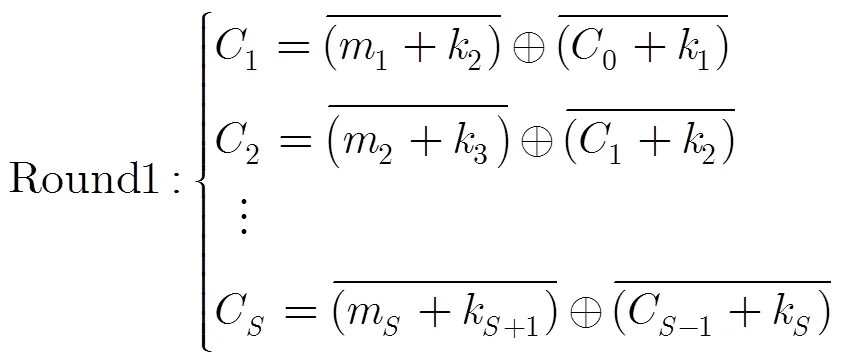
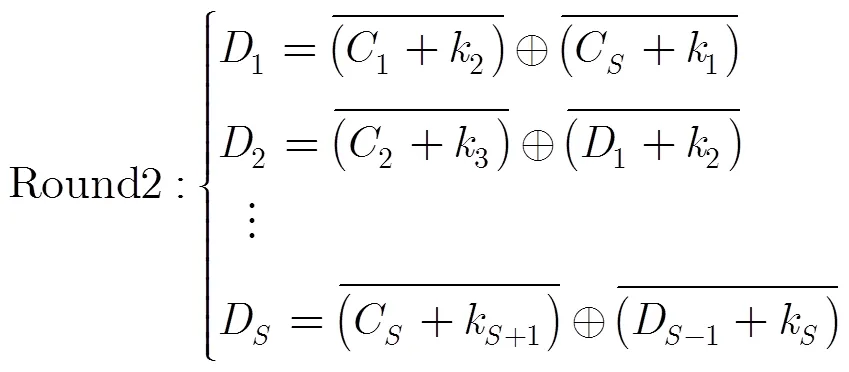
3.4 解密步骤

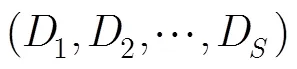
3.5 密钥文件

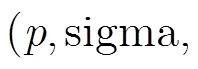
表1系统密钥文件

参数功能 p, sigma混沌系统参数 dim, e, X1, X2,,Xdim耦合格子映射参数 C加密系统启动参数 RND真随机数

4 系统测试

4.1 基本测试

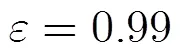
由图4可知，加密后的图像没有明显的规律性，而且其灰度值大致均匀。对加密前后的图像像素值统计对比分析如图5所示。图5(a)表示原始图像的灰度直方图，图5(b)表示加密图像的灰度直方图，可见加密之后的图像灰度分布与原始图像相比有较大的改变，它近似为均匀分布。

图4 加密前后对比

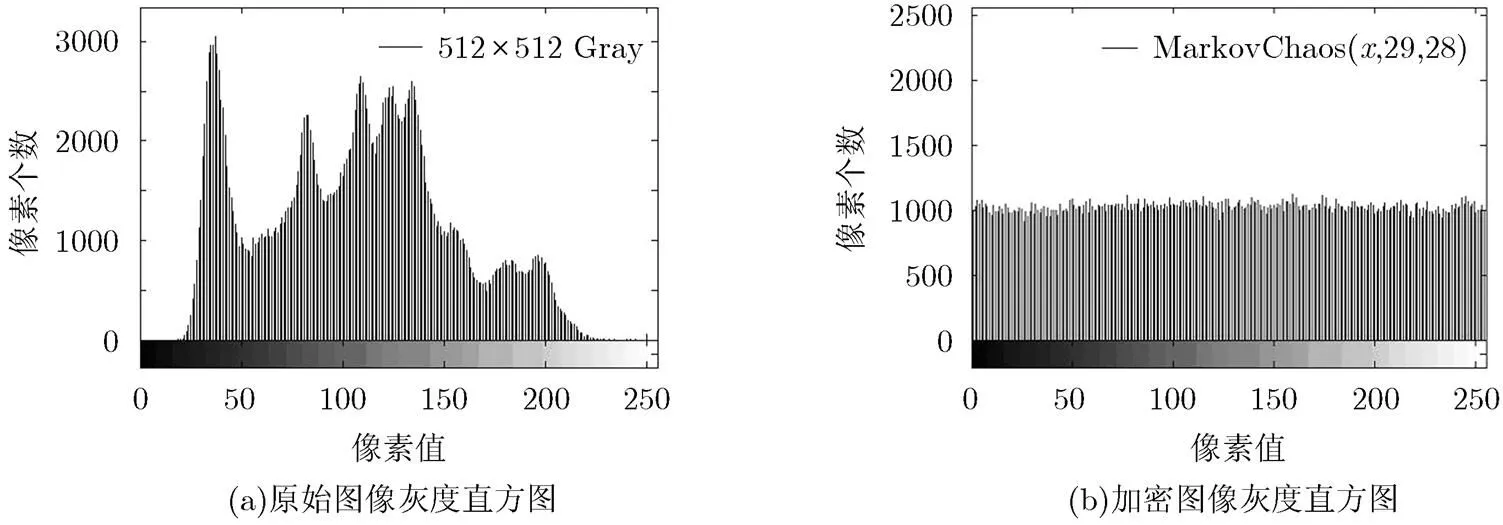
图 5加密前后图像像素分布直方图对比

对图像进行2维傅里叶变换分析可知其原始图像的频谱中心化后如图4(b)所示，加密后的图像做傅里叶变换如图4(d)所示。通过比较可知，原图像在中心位置的能量较高。图像像素值可构成一个曲面，由图4(b)可知此曲面的低频部分能量较高，而高频部分能量较低，而图4(d)是加密后的图像，其高频和低频部分能量无明显差异，其能量分布整体上比较均匀。

4.2 安全性分析

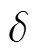
表2加密前后的相关系数对比

方向原始图像加密图像 水平0.9704-0.0601 垂直0.9782-0.0577 对角0.9851 0.0092

由表2可知，原始图像在3个方向上的相关性比较大，而加密图像却比较小。这主要是因为原始图像像素变化大致连续，相邻的像素值差别不太大，所以相关度比较高，而密文图像相邻像素变化剧烈，故其在3个方向的相关度都比较低。传统的分组密码算法(如DES和AES算法)在应用于图像加密时，密文图像的相关性比较强，这将导致图像相邻像素的关联信息泄露，而本文的密码算法相对来说更有优势。

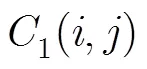
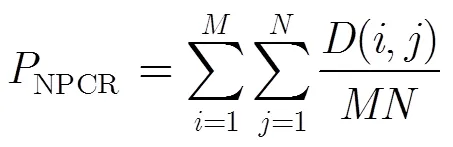
通过在原始图像中的起始部分，中间部分和末尾部分选取100个组对比实验，每次仅改变明文的一个比特，那么对应密文的NPCR值如图6(a)所示，其变化率的均值接近于算法所能达到的理想值。与文献[16]等提出的算法相比，本文的算法对明文变化更敏感，且具有更强的抗差分攻击能力。

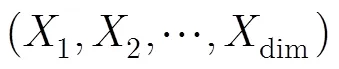
4.3算法效率

混沌密码算法所用混沌系统迥异，算法结构各不相同，安全性也有区别。本文先从密钥流生成的角度对它们进行分析。对基于微分方程的混沌系统来说，若采用四阶龙格库塔方法求解，每产生一个新的输出，Lorenz系统需要25次加法，25次乘法和2次除法操作，超混沌系统需要36次加法，44次乘法和2次除法操作。Logisitc映射需要1次加法和2次乘法操作。本文的混沌系统需要3次加法，2次乘法，1次除法和1次模1操作(复杂度小于加法)。加耦合格子后需要30次加法，18次乘法，6次除法和6次模1操作。故本文密钥流生成效率比文献[8,12]高，再从加解密操作来看，运算量与文献[8, 12]相当。故本文算法效率更高。若从并行计算角度来看本文的算法效率更容易提升，且耦合格子的使用效率可进一步提高。

实验硬件环境为Pentium(R) Dual-Core 2.6 GHz CPU, 2 G内存的PC机，软件环境为Windows XP操作系统 Matlab 2009平台。与基于连续映射的超混沌设计的密码算法[14]相比，在产生4096 bit长度密钥时，基于超混沌的算法需要43.4375 s，基于Lorenz 系统的混沌系统需要时间10.8906 s，而本文算法仅需0.1563 s。另外，基于耦合格子映射的系统有比较好的并行结构，在FPGA上实现时可达到更高的运算效率。由此可见，本文密码算法与建立在微分方程系统上的连续混沌系统相比有更大的速度优势。

4.4 与已有方案对比分析

首先，直接使用Logistic等映射构造密码算法时，其分布并不均匀，产生序列的极限分布特点会泄露所用混沌系统的参数信息，本文使用的混沌系统的极限分布是均匀分布的，不会泄露这部分信息。然后，由本文图1(a)可知，本文所用的混沌映射比直接使用Logistic映射和Tent映射产生的序列的复杂度高，其随机性更好。其次，由2.2节可知，当直接使用低维的混沌系统构造密码算法时，因计算精度的限制，其密钥空间往往不够大而难以抵抗穷举攻击，利用本文提出的改进时空混沌可以简便地提升系统的密钥空间，还可以使密钥分布有更好的均匀性。另外，改进时空混沌采用周期边界约束，可以抵抗文献[19]提出的基于常数驱动的攻击。再次，通过采用不同群中的混合运算，可以抵抗文献[3~8]算法所面临的选择明文(CPA)和选择密文攻击(CCA)，与其相比具有更高的安全性。最后，通过引入随机数构造了一种概率密码，使得相同的明文可以产生不同的密文，从而达到一次一密的效果，这是目前诸多文献中未曾见到的。

5 结束语

本文应用一种新的混沌系统设计了一种新的混沌图像密码算法，分析可知此图像密码算法加密后的图像难以辨识，图像的统计分析表明其频谱图和像素直方图也没有可以分辨的特征。进一步的安全性分析可知，该算法破坏了原始图像相邻像素的相关性，有着比较理想的明文敏感性和密钥敏感性。与基于超混沌的密码算法相比，本文的密码算法在效率上更有优势。通过改进本文的图像密码算法可以达到更高的效率，表明本文的算法在实际应用中将有着不错的前景。

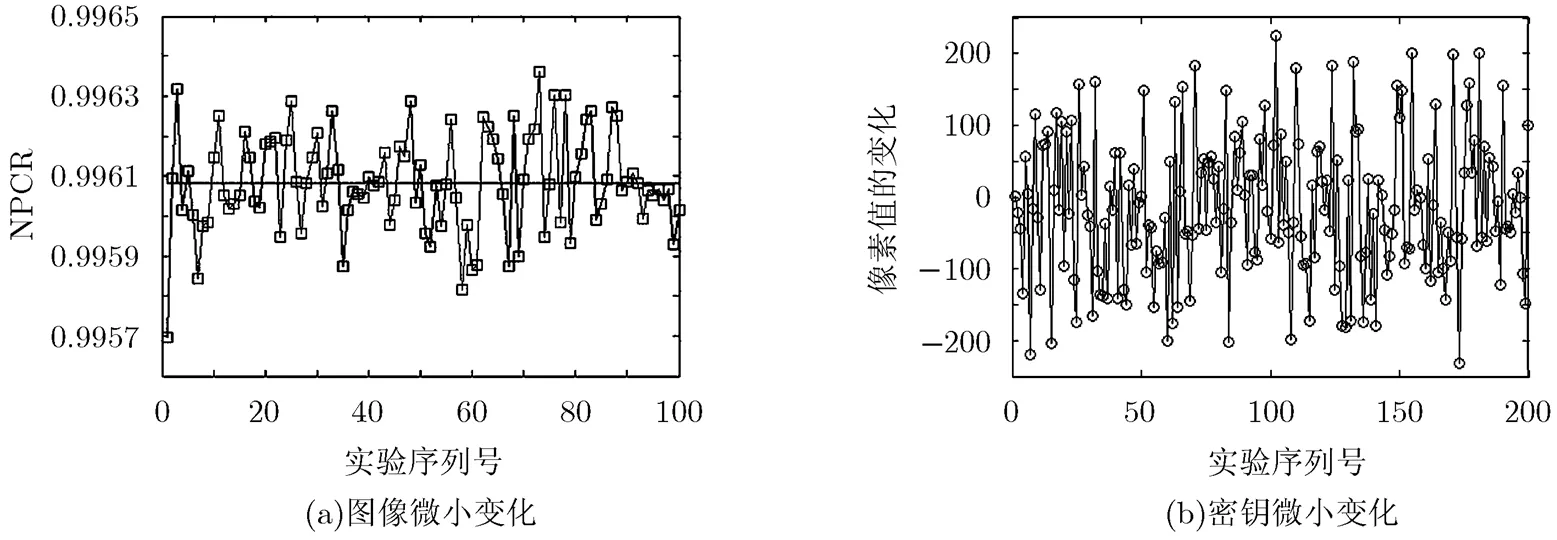
图6 系统输入微小变化时的NPCR值

[1] Socek D, Magliveras S, C’ulibrk D,.. Digital video encryption algorithms based on correlation-preserving permutations[J]2007, DOI.10.1155/2007/52965.

[2] Ji W Y and Hyoungshick K. An image encryption scheme with a pseudorandom permutation based on chaotic maps[J]., 2010, 15(12): 3998-4006.

[3] Baptista M S. Cryptography with chaos[J]., 1998, 240(1): 50-54.

[4] Fridrich J. Symmetric ciphers based on two-dimensional chaotic maps[J].,1998, 8(6): 1259-1284.

[5] Tong Xiao-jun. Design of an image encryption scheme based on a multiple chaotic map[J]., 2013, 18(7): 1725-1733.

[6] 黄峰, 冯勇. 利用图像分割思想的二维混沌映射及图像加密算法[J]. 光学精密工程, 2007, 15(7): 1096-1103.

Huang Feng and Feng Yong. Novel 2D chaotic map based on image segmentation and image encryption approach[J]., 2007, 15(7): 1096-1103.

[7] 李娟, 冯勇, 杨旭强. 三维可逆混沌映射图像加密及其优化算法[J]. 光学精密工程, 2008, 16(9): 1738-1745.

Li Juan, Feng Yong, and Yang Xu-qiang. Invertible chaotic 3D map based image encryption and its optimized algorithm [J]., 2008, 16(9): 1738-1745.

[8] 王静, 蒋国平. 一种超混沌图像加密算法的安全性分析及其改进[J]. 物理学报, 2011, 60(6): 060503.

Wang Jing and Jiang Guo-ping. Cryptanalysis of a hyper-chaotic image encryption algorithm and its improved version[J]., 2011, 60(6):060503.

[9] Chen Guan-rong, Mao Yao-bin, and Charles K C. A symmetric image encryption scheme based on 3D chaotic cat maps[J].,, 2004, 21(3): 749-761.

[10] Ercan S, Cahit C, and Olcay T Y. Cryptanalysis of Fridrich’s chaotic image encryption[J]., 2010, 20(5): 1405-1413.

[11] Kanso A and Ghebleh M. A novel image encryption algorithm based on a 3D chaotic map[J].2012, 17(7): 2943-2959.

[12] Li Shu-jun, Li Cheng-qing, Chen Guan-rong,.. Cryptanalysis of the RCES/RSES image encryption scheme[J]., 2008, 81(7): 1130-1143.

[13] 刘泉, 李佩玥, 章明朝, 等. 一类具有Markov性质的混沌系统的构造[J]. 物理学报, 2013, 62(17): 170505.

Liu Quan, Li Pei-yue, Zhang Ming-chao,. Construction of a class of chaos systems with Markov properties[J].2013, 62(17): 170505.

[14] 朱从旭, 胡玉平, 孙克辉. 基于超混沌系统和密文交错扩散的图像加密新算法[J]. 电子与信息学报, 2012, 34(7): 1735-1743.

Zhu Cong-xu, Hu Yu-ping, and Sun Ke-hui. New image encryption algorithm based on hyperchaotic system and ciphertext diffusion in crisscross pattern[J].&, 2012, 34(7): 1735-1743.

[15] Azad R K, Rao J S, and Ramakrishna R. Information-entropic analysis of chaotic time series: determination of time delays and dynamical coupling[J].&, 2002, 14(4): 633-641.

[16] Garcia P, Paravano A, Cosenza M G,. Coupled map networks as communication schemes[J]., 2002, 65(4): 045201.

[17] 陈莎莎, 张建忠, 杨玲珍, 等. 基于混沌激光产生1 Gbit /s 的随机数[J]. 物理学报, 2011, 60(1): 010501.

Chen Sha-sha, Zhang Jian-zhong, and Yang Ling-zhen,.. One Gbit/s random bit generation based on chaotic laser[J]., 2011, 60(1): 010501.

[18] Wang Xing-yuan and Xie Yi-xin. Cryptanalysis of a chaos-based cryptosystem with an embedded adaptive arithmetic coder[J]., 2011, 20(8): 080504.

[19] 王开, 裴文江, 周建涛, 等. 一类时空混沌加解密系统的安全分析[J]. 物理学报, 2011, 60(7): 070503.

Wang Kai, Pei Wen-jiang, Zhou Jian-tao,.. Security of chaos-based secure communications in a large community[J].2011, 60(7): 070503.

刘 泉： 男，1985年生，博士生，研究方向为混沌密码学、网络信息安全和嵌入式系统.

李佩玥： 男，1985年生，助理研究员，研究方向为网络信息安全、嵌入式系统、混沌密码和精密控制技术研究.

章明朝： 男，1982年生，副研究员，研究方向为光电探测、信息安全及信息融合研究.

隋永新： 男，1970年生，研究员，研究方向为网络信息安全、光学信息融合及深紫外光刻技术研究.

杨怀江： 男，1966年生，研究员，研究方向为网络信息安全、光学信息融合及深紫外光刻技术研究.

Image Encryption Algorithm Based on Chaos System having Markov Portion

Liu Quan①②Li Pei-yue①Zhang Ming-chao①Sui Yong-xin①Yang Huai-jiang①

①(,,,,130033,)②(,100039,)

In order to construct a high complexity, secure and low cost image encryption algorithm, a class of chaos with Markov properties is studied and used to build the encryption algorithm. First, the key stream generator is designed by the Markov Chaos with changeable parameters and the improved spatiotemporal chaos. Then, a true uniform random number generator is used to disturb the original key of the algorithm, which can dynamically change the mixed matrix and the key stream. Finally, the diffusion function is built by two iterations of the round function which is composed of different kinds of additions in different groups to increase the complexity of decipher. The experiments indicate that the key stream possesses good statistical properties, and the characteristic of the original image is broken which makes the cipher image undistinguishable. The further analysis indicates that the proposed algorithm can resist some known attacks like differential attacks, and the proposed algorithm is more efficient than the existed algorithms based on super chaos. Additionally, the proposed algorithm is easy to realize and can satisfy the security and efficiency requirements, which indicates promisingapplications.

Image encryption; Chaos; Markov portion; Spatiotemporal chaos

TP309.7

A

1009-5896(2014)06-1271-07

10.3724/SP.J.1146.2013.01246

刘泉 lovefirespread@gmail.com

2013-08-19收到，2013-11-21改回

国家973规划项目(2007CB311201)，应用光学国家重点实验室开放基金(Y1Q03FQK02)和吉林省科技发展计划项目(20130522120JH)资助课题