一种水声通信中的多阵元Turbo均衡算法

许 浩 朱 敏① 武岩波



一种水声通信中的多阵元Turbo均衡算法

许 浩②③朱 敏①②③武岩波*①②

①(中国科学院声学研究所声场声信息国家重点实验室 北京 100190)②(中国科学院声学研究所海洋声学技术实验室 北京 100190)③(中国科学院大学 北京 100190)

Turbo均衡应用在水声通信中的问题主要在于水声信道时间扩展长，多接收阵元处理复杂度较高。该文研究了将时间反转与马尔可夫链蒙特卡罗(MCMC)均衡联合优化算法用于实现Turbo均衡。首先进行时间反转实现多接收阵元较长多径时延的压缩，再利用白化滤波器解决时间反转造成的噪声模型失配问题，最后利用复杂度较低的MCMC均衡器结合软迭代信道估计对时间反转合并后得到的信号进行均衡。结合真实实验信道条件对信道响应估计的误差建立模型，通过仿真比较得出，该算法在相同条件下相对于多阵元直接自适应Turbo均衡算法复杂度降低67%，且有1.6 dB的误码率性能增益。通过对湖上试验数据进行处理，进一步验证了该算法的优势。

水声通信；时间扩展；时间反转；白化滤波器；马尔可夫链蒙特卡罗均衡

1 引言

时间反转多阵元合并是近年来在水声通信中较为广泛使用的多阵元联合处理手段，其极大地压缩单个阵元接收信号较长的时延并有效的利用信号的能量[11,12]。时间反转与判决反馈均衡器级联在水声通信中有较好的效果[13,14]，然而水声通信中Turbo均衡技术尚没有考虑时间反转可以极大简化后级均衡的复杂度，因而Turbo均衡在实际工程中较高的复杂度使其难以实用。

可见，选择复杂度较低且高性能的均衡算法对Turbo均衡在水声通信中应用至关重要。本文提出的时间反转合并与MCMC均衡联合算法，基于优势互补的思想，并加以改进以实现低复杂度和高性能的目标，其特点是：(1)使用时间反转多阵元合并，其具有降低后级均衡器阶数，且不依赖于其它参数的选择，使得其可以简化均衡算法的设计。在时间反转合并后，使用了利用接收信号信息的重构白化滤波器，使得合并生成的单路信号中噪声为高斯白噪声，满足了MCMC均衡算法基于信道噪声为高斯白噪声的假设，解决了噪声模型失配问题。(2)使用复杂度较低性能较优的MCMC均衡算法，对时间反转合并后的单路信号进行均衡[15,16]，迭代中，MCMC均衡需要的信道与误差方差由软迭代信道估计器利用译码器反馈的软信息进行处理获得。

2 系统模型

图1为时间反转与MCMC联合优化Turbo均衡相干通信系统模型。信息比特通过并行级联Turbo编码器，经过星座映射后发射。信号经过水声信道后被多个阵元接收信号，然后时间反转多阵元合并多阵元信号，最后MCMC均衡译码输出信息比特。

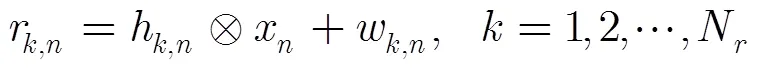
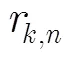
3 时间反转与MCMC联合Turbo均衡算法

3.1 时间反转多阵元合并

水声通信中接收到的信号时间扩展较长，较多的阵元数量使得均衡处理的难度较大，时间反转是降低后级均衡复杂度的有效方法。文献[13]给出时间反转合并的单路信号为

图1 时间反转与MCMC联合均衡水声通信系统传输模型

3.2 基于噪声样本构建的白化滤波器

时间反转多阵元处理将时间扩展较长的多阵元信号合并为时间扩展较短的单路信号，各阵元的高斯白噪声将被合并成有色高斯噪声。为了达到更优越的均衡效果，将时反与基于高斯白噪声假设的MCMC均衡器联合时，将出现噪声模型失配问题。为了避免噪声模型失配问题，对时反处理得到的单路信号进行白化处理。

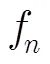
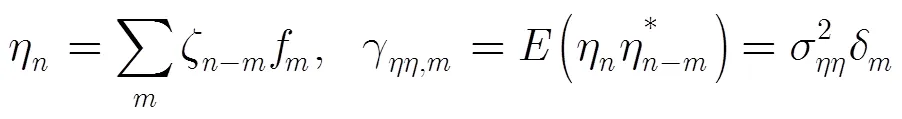
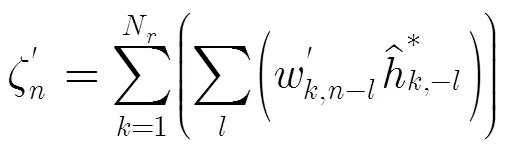
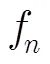
对于时间反转合并的处理过程可以进一步从式(2)转化为

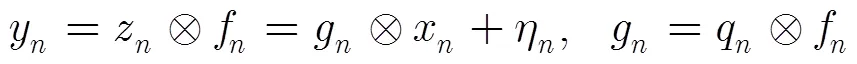
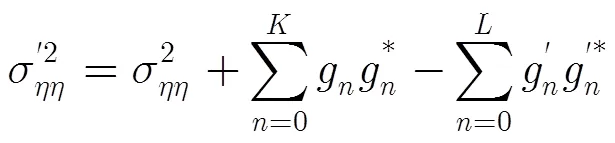
3.3 基于软迭代信道和误差方差估计的MCMC均衡算法

MCMC均衡是最优MAP均衡器的降低复杂度实现，文献[9]指出，其在信道以及噪声特性完全已知条件下接近最优MAP均衡器的性能。但是在真实通信情况下，信道响应和噪声方差均未知，因而限制了其在实际中的应用。本文将MCMC均衡算法扩展，利用软迭代信道估计器提供的信道和误差方差估计，在每次均衡译码迭代时更新均衡器参数。文献[15]中提出软迭代信道估计算法，其误差方差的估计没有封闭计算公式作为依据，本节给出误差方差的构成分析，并使用均值处理得到误差方差的估计，使其具有封闭的计算公式。参考式(6)中的卷积形式，软迭代信道估计器在最小均方算法下的信道估计更新方程为

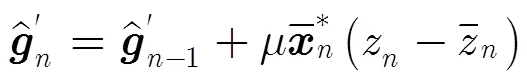
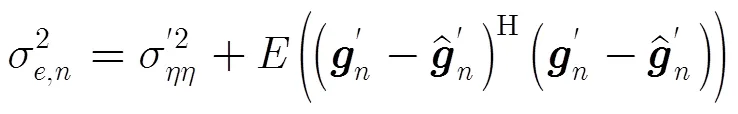
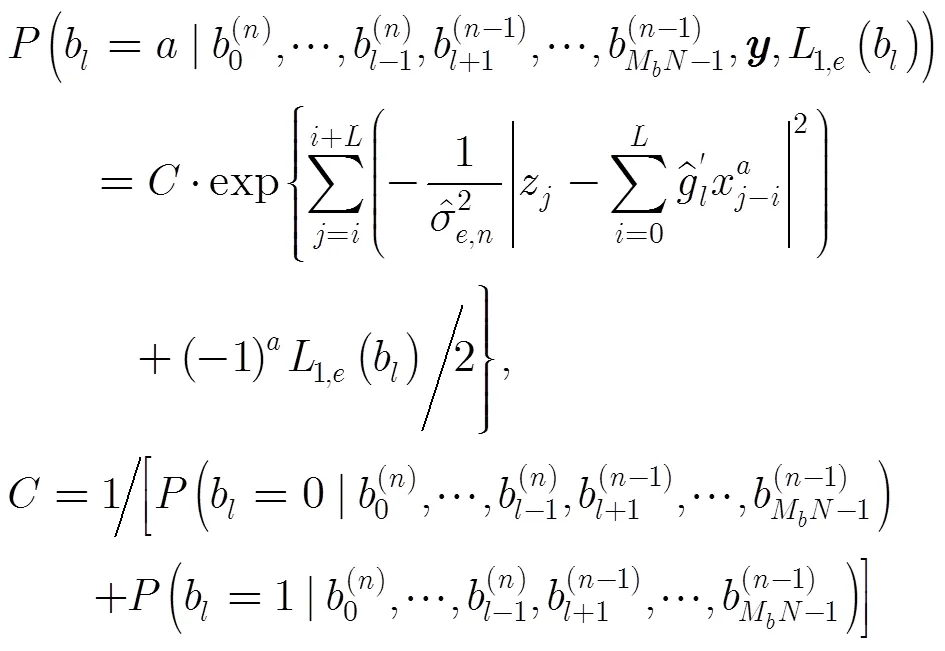
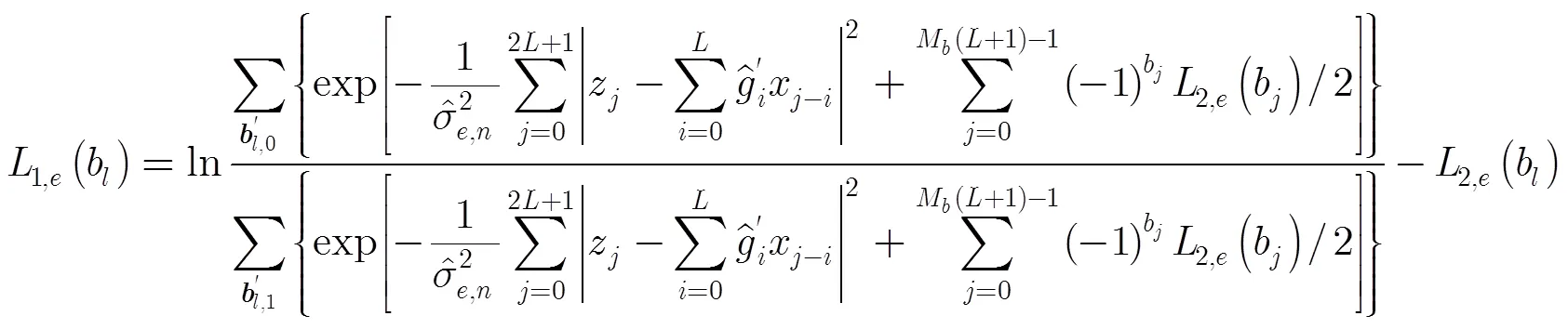
MCMC均衡算法流程如表1所述。

表1 MCMC均衡算法流程

4 仿真分析

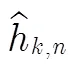
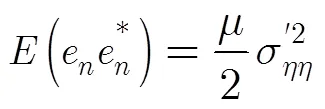
信道的信噪比设置根据Turbo码的码率以及QPSK调制方式如式(14)所示。

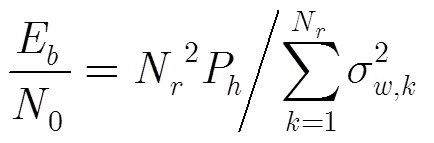
此外，在相同的信噪比以及信道条件下，依照文献[4]在相同信噪比下进行自适应多阵元Turbo均衡器均衡系数的建模。为了方便比较，两种Turbo均衡译码的最大迭代次数都为5，其中时间反转MCMC联合Turbo均衡的吉布斯采样算法迭代次数为10，其使用的信道估计器估计的信道扩展为10个符号长度。而多阵元自适应Turbo均衡的前馈滤波器和反馈滤波器长度分别为400和200。由于时间反转MCMC联合Turbo均衡算法复杂度取决于吉布斯采样迭代次数与信道响应长度的乘积，且呈线性关系，而多阵元自适应Turbo均衡复杂度也与前馈反馈阶数之和呈线性关系，可以得出时间反转MCMC联合Turbo均衡算法复杂度大约为多阵元自适应Turbo均衡复杂度的33%左右。

本文选取真实实验中采集的4个阵元信号经过信道估计后得到的信道冲激响应来进行仿真，符号速率为4k symbol/s，如图2(a)所示信道冲激响应的时间扩展约为20 ms。图2(b)为4个阵元时间反转合并后，生成的单路信号，经过信道估计后得到的信道冲激响应，由于时间反转合并经过白化以后，信道冲激响应聚焦效果明显，只截取了部分能量集中的冲激响应方便显示。

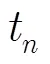
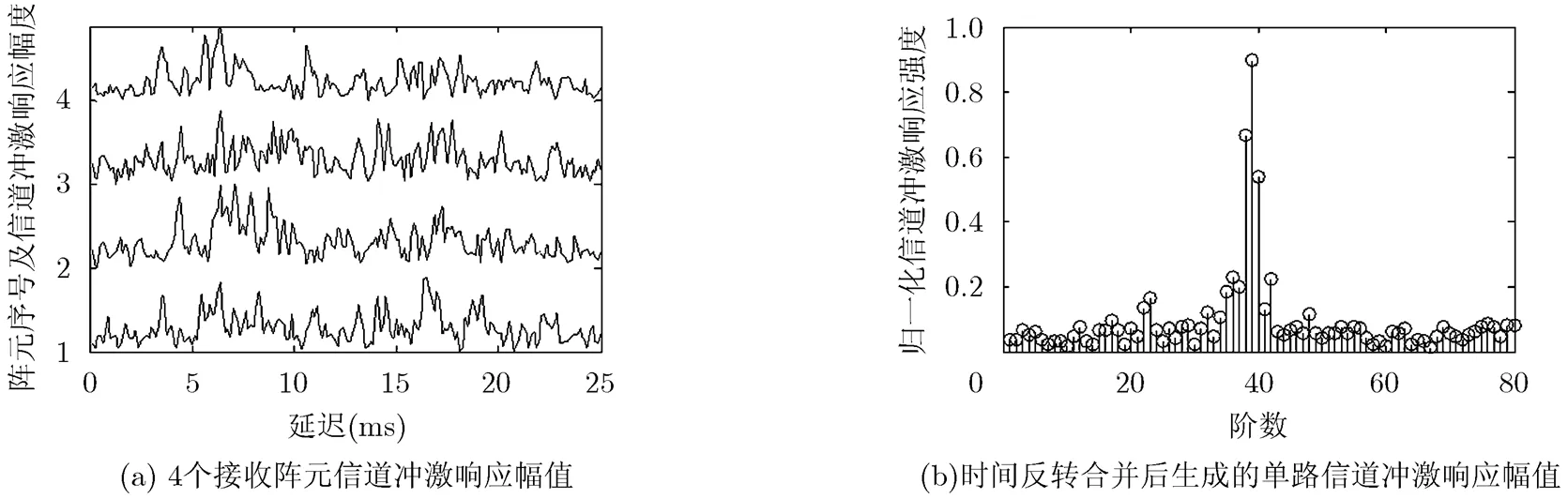
图2 信道冲激响应幅值

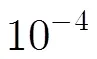
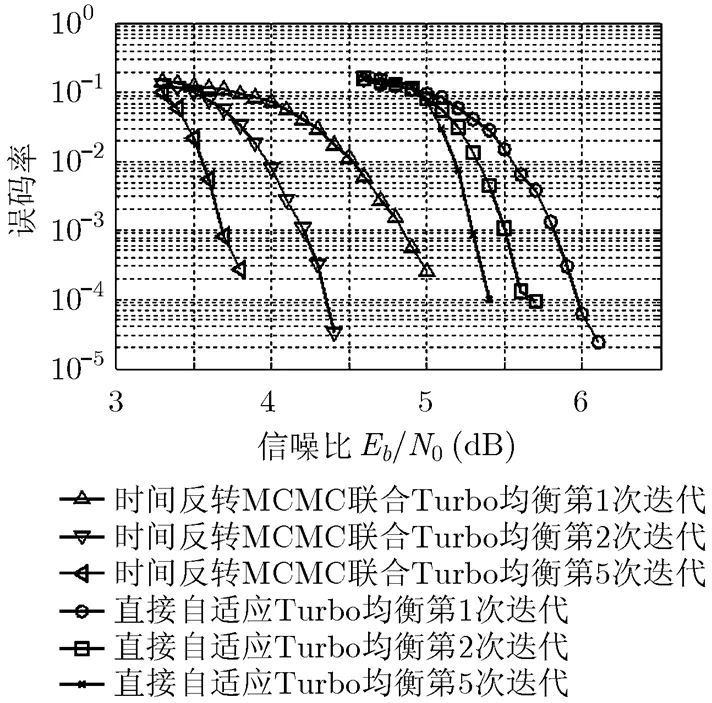
图3 两种均衡器算法的误码率性能比较

5 湖试数据处理

为了验证本文提出的时间反转MCMC联合Turbo均衡算法对水声信道的通信性能，本文对2012年进行的千岛湖试验数据进行处理并分析。此数据的产生条件为：通信距离为1100~2200 m，接收阵列(包含4个接收阵元)在一个固定船体下方，接收阵元深度12~18 m，发射阵深度20 m。

图4(a)为一次发射14帧信号内，对单个阵元信道估计得到的信道变化情况，而图4(b)给出了时间反转后得到的单一信道变化情况，可知时间反转合并后极大地压缩了相对于原单一阵元信道造成的时间扩展，并且信道变化较小。结合图4(a)和图4(b)可知，在一次发射间隔内信道的时延扩展达到了20 ms，相对于发射的符号率，这样的时延使得直接对阵元接收数据进行均衡的均衡器阶数较大。

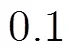
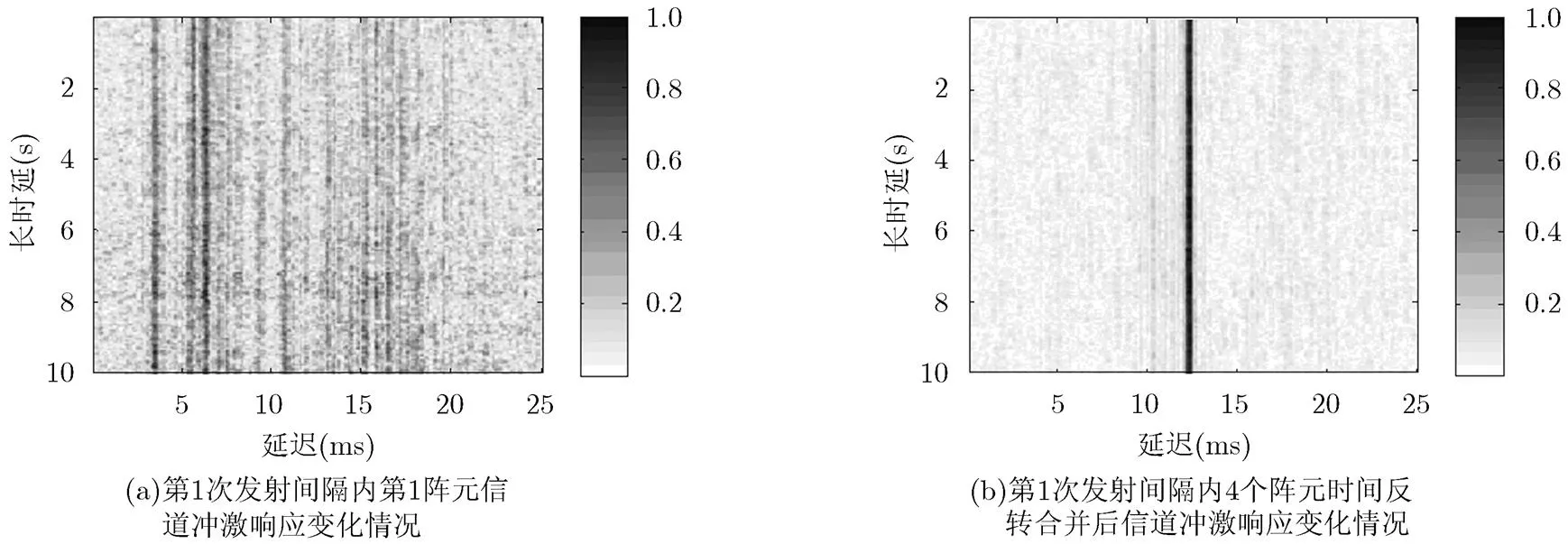
图4 信道变化情况

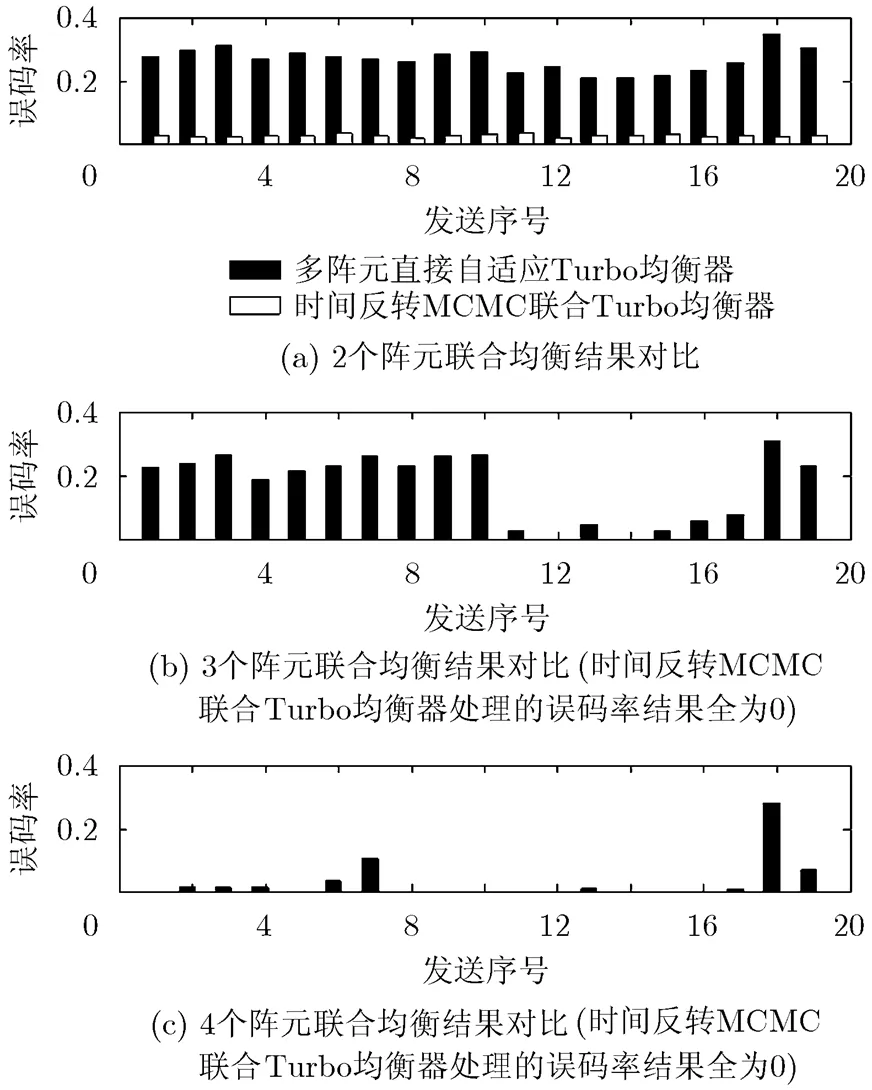
图5 19次发射试验数据处理误码率分析

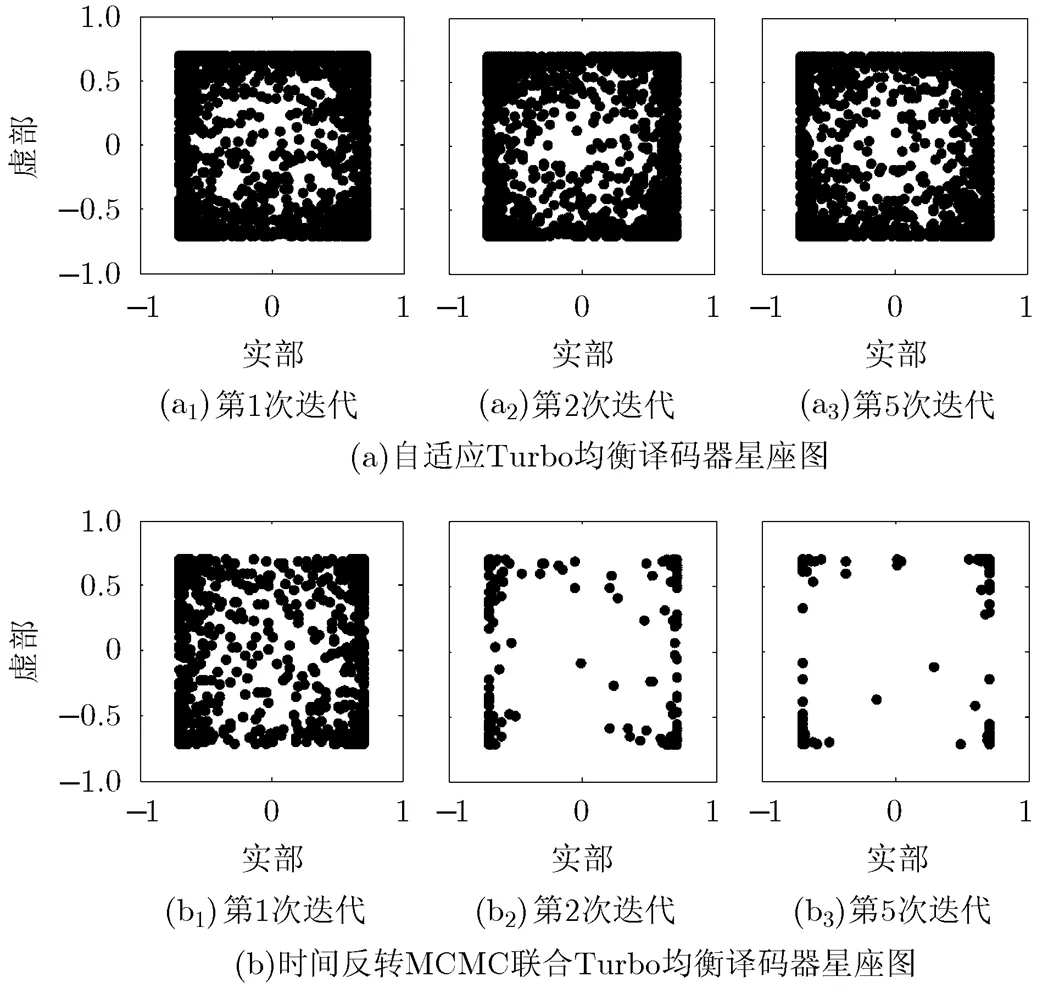
图6 迭代输出星座图

综上所述，通过对真实湖试数据的处理可以得到时间反转MCMC联合Turbo均衡算法性能在相同条件下，要明显优于多阵元直接自适应Turbo均衡器。

6 结论

针对Turbo均衡在水声通信中问题主要存在于多阵元处理以及信道扩展较长，本文提出了时间反转MCMC联合Turbo均衡算法。由仿真结果可知，时间反转MCMC联合Turbo均衡算法的性能明显优于文献[7]中提出的多阵元直接Turbo均衡算法，且可以在更低的信噪比下达到零误码率。从湖试数据处理中可以看出，本文提出的算法为多阵元水声相干通信提供更可靠的性能，并且算法复杂度在工程实现上更加可行。

[1] Stojanovic M, Catipovic J A, and Proakis J G. Phase-coherent digital communications for underwater acoustic channels[J]., 1994, 19(1): 100-111.

[2] Tuchler M and Singer A C. Turbo equalization: an overview[J]., 2011, 57(2): 920-952.

[3] Otnes R and Eggen T H. Underwater acoustic communications: long-term test of turbo equalization in shallow water[J].2008, 33(3): 321-334.

[4] Walree P A and Leus G. Robust underwater telemetry with adaptive turbo multiband equalization[J].2009, 34(3): 645-656.

[5] Rafati A, Lou H, and Xiao C. Soft-decision feedback turbo equalization for LDPC-coded MIMO underwater acoustic communications[J]., 2013, 38(1): 1-10.

[6] Yellepeddi A and Preisig J C. Soft-adaptive turbo equalization: using soft information in adaptation[C]. Proceedings of Signals, Systems and Computers (ASILOMAR), Pacific Grove, 2012: 1541-1546.

[7] Choi J W,Riedl T J, and Kim K. Adaptive linear turbo equalization over doubly selective channels[J]., 2011, 36(4): 473-489.

[8] Meng Qing-wei,Huang Jian-guo, and Han Jing. An improved direct adaptive multichannel turbo equalization scheme for underwater communications[C]. Proceedings of IEEE OCEANS Conference, Yeosu, 2012: 221-225.

[9] Wang Hong, Chen Rong-rong, and Choi Jun Won. Markov chain monte carlo detection for frequency-selective channels using list channel estimates[J]., 2011, 5(8): 1537-1547.

[10] Peng R H, Chen R R, and Behrouz F B. Markov chain monte carlo detectors for channels with intersymbol interference[J]., 2010, 58(4): 2206-2217.

[11] Nie Xing-yan, Xu Wen, and Zhen Jia-chun. Time reversal acoustic communication with concatenated reed-solomon code[C]. Proceedings of IEEE OCEANS Conference, Yeosu 2012: 221-225.

[12] Aijun S,Badiey M, and McDonald V K. Time reversal receivers for high data rate acoustic multiple-input multiple-output communication[J]., 2011, 36(4): 525-538.

[13] Rouseff D. Intersymbol interference in underwater acoustic communications using time-reversal signal processing[J]., 2005, 117(3): 780-791.

[14] Xia M, Xu W, and Pan X, Time reversal based channel tracking for underwater acoustic communications[C]. Proceedings of the Seventh ACM International Conference on Underwater Networks and Systems, Los Angeles, California, 2012: 1-5.

[15] Otnes R and Tuchler M. Iterative channel estimation for turbo equalization of time-varying frequency-selective channels[J]., 2004, 3(6): 1918-1923.

[16] 唐怀东, 朱敏, 武岩波. 一种水声信道Turbo均衡中的软迭代信道估计算法[J]. 电子与信息学报, 2013, 35(3): 677-682.

Tang Huai-dong, Zhu Min, and Wu Yan-bo. An algorithm of soft iterative channel estimation for Turbo equalization of underwarter acoustic communication[J].&, 2013, 35(3): 677-682

许 浩： 男，1990年生，硕士生，研究方向为水声通信、信道均衡.

朱 敏： 男，1971年生，研究员，研究方向为海洋声学及其技术.

武岩波： 男，1982年生，副研究员，研究方向为海洋声学及其技术.

An Algorithm of Multi-array Turbo Equalization of Underwater Acoustic Communication

Xu Hao②③Zhu Min①②③Wu Yan-bo①②

①(,,100190,)②(,,100190,)③(,100190,)

The main problems of the application of the Turbo equalizer in underwater acoustic communication are long time spread of channel and the multi-array processing. The union algorithm of time reversal and Markov Chain Monte Carlo (MCMC) equalization is proposed. Time reversal compresses the long time spread by combining multi-array signal, then the whitening filter is adopted to the solution of the noise model mismatch, at last the MCMC equalizer under optimal Maximum(MAP) criterion realizes the soft-in soft-out equalizer with the channel information obtained by channel estimation of soft iteration. The simulation based on the real experimental condition is conducted for the error model of truncated channel estimation. Simulation results denote that, this algorithm gets 1.6 dB Bit Error Rate (BER) performance gain, and 67% complexity loss over adaptive Turbo equalization. In the real experiment conducted in a lake,result of dataprocessing denotes that the union algorithm of time reversal and MCMC equalizer have a superior performance over the algorithm of multichannel adaptive Turbo equalizer.

Underwater acoustic communication; Time spread; Time reversal; Whitening filter; Markov Chain Monte Carlo (MCMC) equalization

TN929.3

A

1009-5896(2014)06-1465-07

10.3724/SP.J.1146.2013.01027

武岩波 wuyanbo@mail.ioa.ac.cn

2013-07-11收到，2013-11-01改回

国家863计划项目(2002AA401004, 2009AA093301, 2009AA093601)资助课题