轮胎活络模具Archard磨损模型系数的修正

胡海明 ，赵昕 ，李晓宾

（1.山东省高分子材料先进制造技术重点实验室，青岛科技大学，机电工程学院，山东青岛，266061 2.青岛软控精工有限公司，山东青岛，266101）

1 引言

磨损对轮胎模具耐磨板而言是一个重要的问题，它直接关系到轮胎硫化时胶边的产生。近年来对于磨损规律的研究也有一定的成果，Archard磨损模型就是其中之一。Archard模型的表达式如下：

式中：

W：耐磨板磨损量，mm；

P：磨损表面压应力，MPa；

v：磨损面的相对滑动速度，mm/s；

H：耐磨板的硬度，HB；

K：磨损系数；

a、b、c：修正系数，经验值为1、1、2。

轮胎模具耐磨板的磨损将通过Deform-3D有限元模拟软件对其进行模拟，将试验测得磨损数据与该条件下进行的模拟磨损数据进行对比，通过对a、b、c的调整，获得耐磨板的磨损模型的修正系数，磨损系数依据经验取K=0.005。

2 磨损数据的采集整理与分析

通过磨损装置的磨损试验，采集一定磨损次数下的磨损量进行分析，取耐磨板上13个点，每磨损5000次对耐磨板进行一次厚度测量，测量厚度后取平均值。磨损数据一次回归分析如图1所示（纵坐标：耐磨板厚度值（μm），横坐标：磨损次数（千次））。

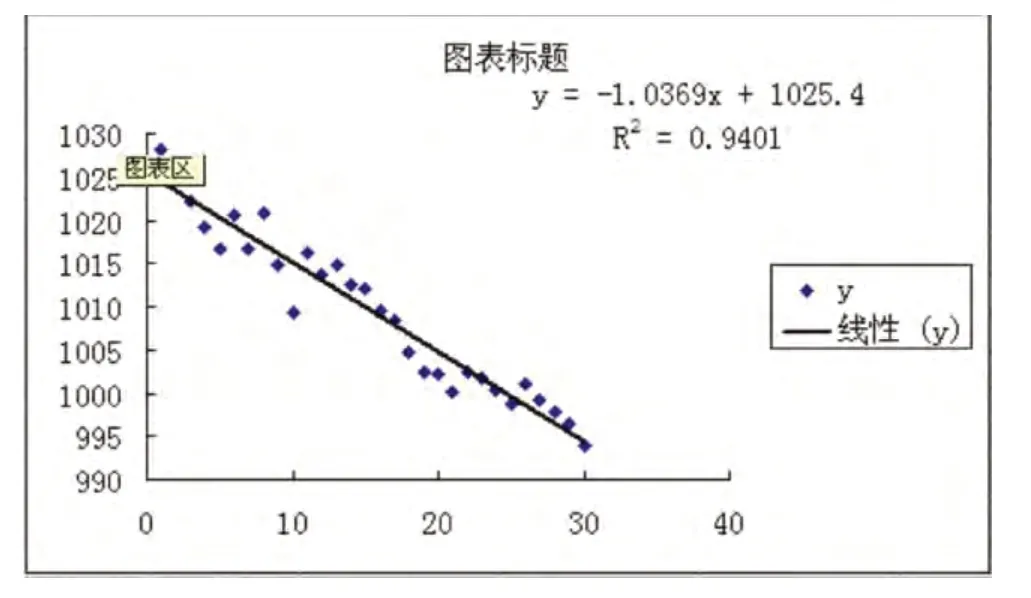
图1 磨损数据线性回归分析

当磨损10次时，根据线性公式计算磨损量：

磨损数据的二次曲线回归分析如图2所示，可以看出二次曲线的曲率也很小R2=0.9427。

图2 磨损数据二次曲线回归分析

综上分析，磨损基本是按照线性规律进行的。

3 a、b、c初始值分析

根据实际磨损量，在K=0.005条件下，对系数a，b，c进行调整。

图3 13点磨损模拟图

取耐磨板上13个点进行磨损模拟，如图3所示。当a=1，b=1，c=2时，用Deform-3D进行有限元模拟，同样在耐磨板上取与实际位置相同的13个点，磨损10个来回。将13个点的磨损量模拟数据取平均值为0.0026823μm。13个点的模拟结果与实测结果进行对比，模拟平均值0.0026823μm大于实测平均值0.0020738μm。

根据先前研究可知，磨损量w随着a的增大而减小，随着b的增大而增大，随着c的增大而减小，对此进行系数a，b，c的调整，见表1。

表1 系数调整比较

由表1可以看出，当a=1，b=0.8963，c=2及a=1.05785，b=1，c=2时模拟磨损量与实际磨损基本一致。

同一种类型的耐磨板其磨损规律是相同的，确定了试验磨损数据的磨损模型系数a、b、c之后，可以模拟活络模具中耐磨板的实际磨损问题。以底座耐磨板为例，，施加在Top Die上的力取1140N，即耐磨板受到的正压力，相对运动速度为12mm/s，硬度50HB。

当取k=0.005，a=1，b=0.8963，c=2时，底座耐磨板磨损量线性方程为：

当取k=0.005，a=1.05785，b=1，c=2时，底座耐磨板的磨损量线性方程为：

其中，y代表磨损量(μm)，x代表磨损次数。

对比发现两组a、b、c条件下，得到模具耐磨板的磨损方程是不同的，所以需要对磨损系数进行修正。

4 a、b、c调整误差分析

由于试验中很多因素的影响，存在误差的原因主要有：

（1）试验装置的稳定性。由于试验需要长时间的磨损来采集数据，装置不停的往复运动，仪器的精度受到了影响，并最终导致采集的磨损数据存在一定的误差；

（2）测量仪器有一定的精度范围，而每次测量的数据数量级很小，故测量数据存在有误差；

（3）在实际测量中，磨损量数据是通过测量指定位置的13个点的磨损量并取其平均值获取的，而每次测量的13个点会有稍微的偏差，这也导致测量的磨损数据存在误差；

（4）Deform-3D的模拟速度是匀速的，而实际磨损运动是一个变速的运动；

（5）由于模拟条件（载荷、速度等）的改变，模拟结果中磨损厚度的分布区域也会有所变化，对于不同的条件下的模拟，后置处理所选的13个点位置却是相同的，因此也会导致一定的偏差。

由于以上原因，调整得到的两组系数最终得到的磨损线性方程是不一样的。

系数a、b、c调整修正

系数a、b、c调整修正采用统计原理，通过多次调整取平均值来减少误差。a、b、c系数粗调范围见表2。

表2 系数编号

对上述a、b、c系数进行不同的组合，并确定其磨损方程，见表3。

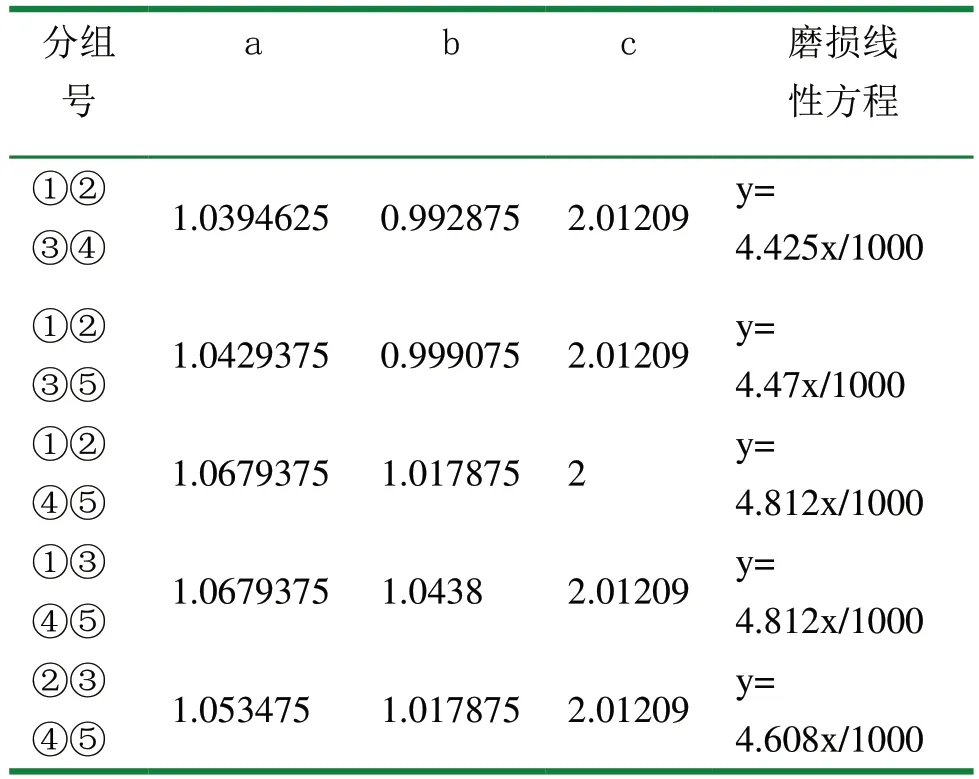
表3 分组结果与对应线性方程

对5个线性方程的系数取平均值可得到平均磨损线性方程为：

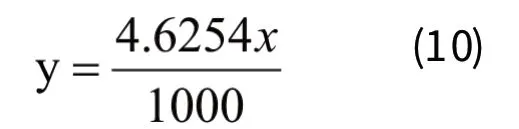
通过上面的数据分析可以看出，分组所取的系数组数越多，最后得到的方程系数偏差越小越集中，主要集中在4.5～4.8之间，在误差允许的范围内，选择开始时对五组系数取平均值得到的结果为本试验最终采用的数据，见表5。

表5 最终方案

5 结论

通过大量的实测磨损数据分析得到耐磨板的磨损基本符合线性规律，对数据进行线性回归归纳其磨损规律，并通过有限元模拟，将得到的模拟数据与实验数据进行对比，根据对比结果调整数学模型系数，最终确定该类型耐磨板的磨损线性方程。

[1]王雷刚，黄瑶，孙宪萍，刘全坤.基于修正Archard磨损理论的挤压模具磨损分析[J].润滑与密封，2006(3):10-11.

[2]张自浩.全钢子午线轮胎活络模磨损模型的研究[D].青岛科技大学，2011.

[3]林高用，冯迪，郑小燕，杨伟，孙利平.基于Archard理论的挤压次数对模具磨损量的影响分析[J].中南大学学报，2009 40(5): 1245-1248.

[4]DEFORM-2D和DEFORM-3D CAE软件在模拟金属塑性变形过程中的应用[J].模具技术，2000（3）：75-80.