气液两相流对板式换热器影响的模拟研究*

张仲彬 刘乐宜 王丙林 徐志明

(东北电力大学能源与动力工程学院)

板式换热器(PHE)由于具有传热效率高、易维护及有效利用低温能源等特点，多年来被广泛应用于各个领域。板式换热器大多应用在液液流动中，随着研究领域的拓展，在现代许多行业的生产设备中都涉及到气液两相流动，所以近些年对于气液两相流动的研究逐渐增多。

两相流各参数的在线实时测量与控制是生产稳定的重要保证[1]。近几年对两相流在微通道中的研究取得了一些成果[2,3]，赵楠用数值方法对垂直入口型微通道中的气液两相流进行了研究[4]，阐述了气泡、气塞的生成原因和过程。Masuo Kaji等研究了微通道中的气液两相流，发现流体流动方向、管道材料和加热条件对流动时的摩擦压降影响不大，并且空隙率随着管子直径的减小而减小[5]。但由于板式换热器中的流动比较复杂，所以关于板式换热器中两相流研究的文献还不是很多。Shiomi Y等研究了混合波纹角人字形板通道中的气液两相流动，发现在水平流动时可观察到层流和扩散流，并且在水平流动中两相流型和压降受上板片波纹角的影响很大[6]。Nilpueng K和Wongwises S对单流道板式换热器中气水两相流进行了研究，发现在逆流垂直向上和向下流动中气水速度对两相压降有很大影响，但两相的流型对压力损失影响不大[7]。Vlasogiannis P等对板式换热器中气液两相流流动形式和传热系数进行了研究，发现当流道中为带有连续气相的流动或以溪流形式流动时对传热特性的改善很有帮助[8]。

为了充分利用板式换热器热损失小、阻力损失小等优点，对气液两相流条件下板式换热器性能的研究是必要的。因此，笔者用数值模拟方法对板式换热器中气液两相流的流动换热和气体在流道中的分布进行了研究，找出适合换热、减小压降的最佳参数，为换热器的经济运行提供依据。

1 换热器的数值计算模型

1.1 物理模型

图1为换热器板片计算物理模型，在图1中：冷热流体单边逆向流动，热流体从上侧流道A端口流进，B端口流出；气液两相冷流体从下侧流道C端口流进，D端口流出。笔者所用的人字形板式换热器的板片材料为304不锈钢，板片参数如下：

外形尺寸 258mm×100mm

试件流程 (1×5)/(1×6)

板间距 2mm

波纹角度 120°

单片有效面积 0.015m2

试件传热面积 0.150m2

当量直径 4mm

波纹深度 2mm

试件片数 12

板片厚度 0.6mm

角孔直径 20mm

波纹法向节距 6mm

单流道截面积 166mm2

图1 板片计算物理模型

1.2 相关假设

由于研究流道内温差较小，采用标准RNGk-ε模型对流道内的流动、换热进行模拟，作如下假设：

a. 热流体和两相冷流体都设为不可压缩的牛顿流体；

b. 忽略动量方程中体积力的影响；

c. 不考虑重力和浮升力产生的影响；

d. 不考虑流体流动过程中由于粘性耗散产生的热效应；

e.流体的进口速度和温度已知，为模拟需要，计算了进口压力和出口温度。

1.3 数学模型

用Fluent数值计算软件，将气相和液相视为连续相，选用欧拉-欧拉双流体模型描述气、液两相流之间的相互作用。其控制方程如下：

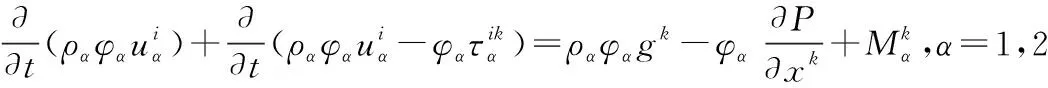
(1)

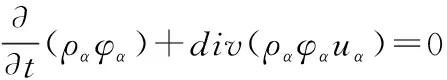
(2)

(3)

式中i、j、k——矢量在x、y、z3个方向上的分量；

uα——介质速度，m/s；

α——代表相态(气相、液相)；

ρα——介质密度，kg/m3；

τα——粘性剪切力，kg/(m·s2)；

φα——体积分数，%。

双流体模型通过动量传递系数λα，β来确定相间的动量传递，气、液两相间相互作用力ψα为：

ψα=∑λα,β(uβ-uα)λα,β=λβ,α≥0

(4)

RNGk-ε模型：

(5)

(6)

式中k——湍动能，是漩涡强度波动变化率，m2/s2；

ε——湍流扩散率，m2/s2。

1.4 边界条件

进口边界设为速度入口，出口边界设为压力出口。外部各边界设为无滑移速度边界条件，中间板片设为换热面，其余各面均为绝热边界，板片壁面材料的参数为：比热容c=644J/(kg·K)，密度ρ=7600kg/m3，导热系数K=644 W/(m·K)。用Pro/e三维软件构建基本物理模型，然后利用Gambit软件，用非结构网格单元对模型进行网格划分。换热器内部流道十分复杂，采用不同的网格步长对不同区域进行划分，然后对网格加密。当主波纹区的网格步长为0.5mm时，平均Nu不发生太大的波动，这时网格密度已经满足模拟精度要求，模型的精度和网格的无关性已在文献[9]中得到验证，模型网格划分如图2所示。

图2 划分网格后的计算模型

2 数值模拟结果与分析

笔者对板式换热器中气液两相单边流动的情况进行了数值模拟，气液两相流体从板片右下侧流入，左下侧流出。以等流速方法进行模拟，选取板间冷热水流速为0.10、0.13、0.15、0.18m/s，空气体积含气率分别为0.10、0.08、0.06、0.04、0.02的工况进行模拟研究。笔者主要以不同空气含气率下，冷热水流速为0.10m/s的模拟结果为例进行说明。

2.1 不同含气率下板间流道中气相的分布

图3为不同空气体积含气率时冷流道中平均气体体积分数的大小分布情况，对比图3a～e可以看出，气体一般在板片接触点处开始聚集，随着气体体积含气率的增大，气体在板间的分布逐渐增多，在进出口连线一侧的气体体积分数比另一侧大，分布更均匀，气体体积分数的最大值出现在板片接触点附近，从而接触点附近的湍动程度最大。

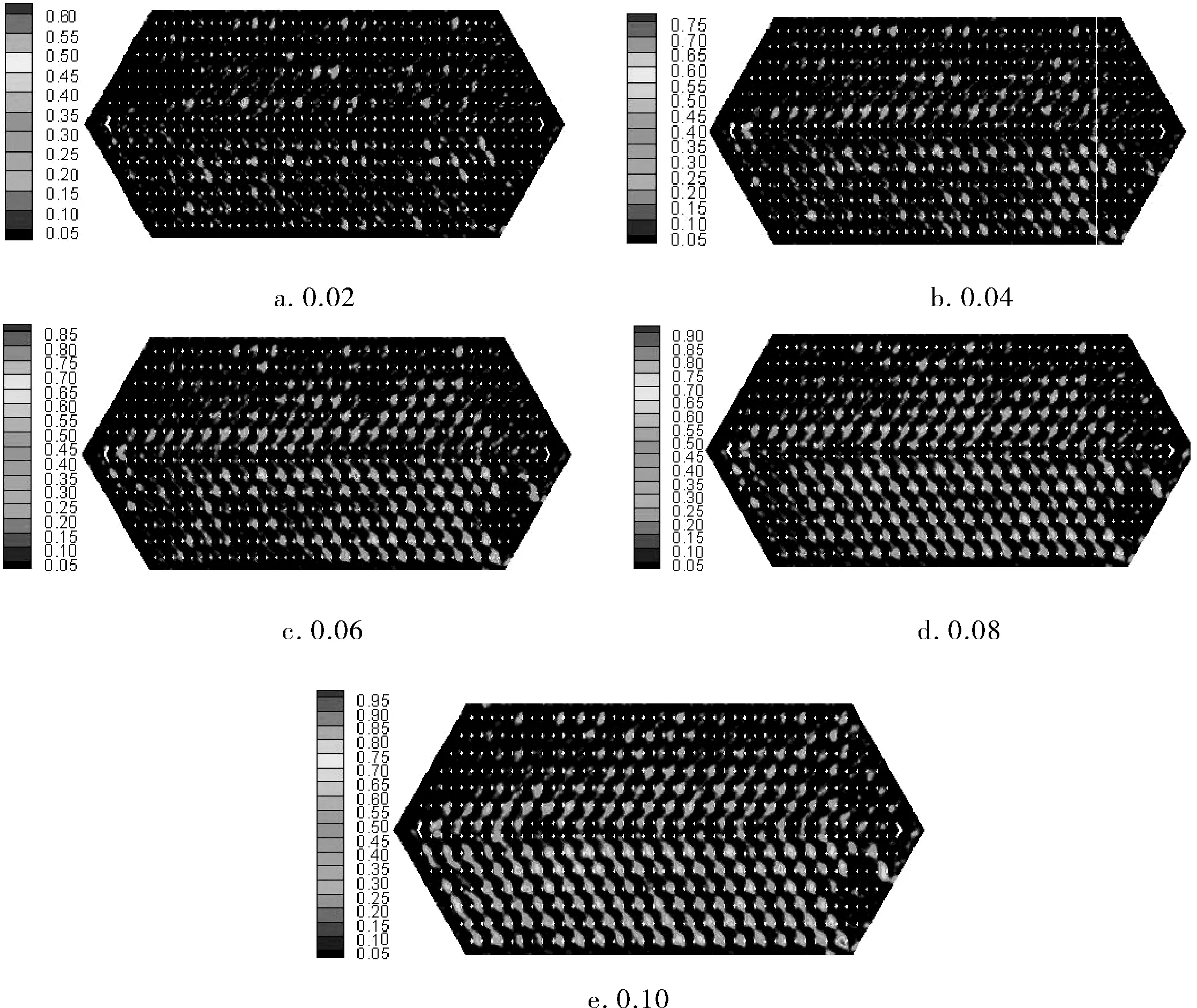
图3 不同空气体积含气率时板间流道中气体体积分数

2.2 不同含气率下冷流道内速度场、压力场和温度场的分布

图4为冷流道y=-0.5mm截面上单相和气液两相的速度大小分布图，对比图4a～f可以看出，流体在板间流动时，在板片边缘和两板片接触点附近流速较慢，这是由于接触点处气体的阻力作用造成的，但流道中气液两相速度明显大于单相速度。两相流体刚进入主流区，由于流道截面积变小，又由于气体的湍动作用，流速急剧增大的情况，并且流道中其他位置的流速都有明显增大。由图中还可看到，含气率为0.02时流道内的速度整体较大，含气率为0.08时流道内的速度稍小，其他含气率时两相流体在流道内各处的速度相差不大。

图4 冷流道y=-0.5mm截面上单相和两相流体速度分布

图5为冷流道中单相和气液两相的压力分布情况，由图5可知，随着流体在板间的流动，压力逐渐降低，并且两相的压力梯度明显大于单相，这是由于板间气体对流体的扰动造成的阻力损失所致；对比图5b～f可以看出，随着含气率的增大，两相流体进出口的压差逐渐减小，其中含气率为0.02时进出口压差最大，含气率为0.10时进出口压差较小。

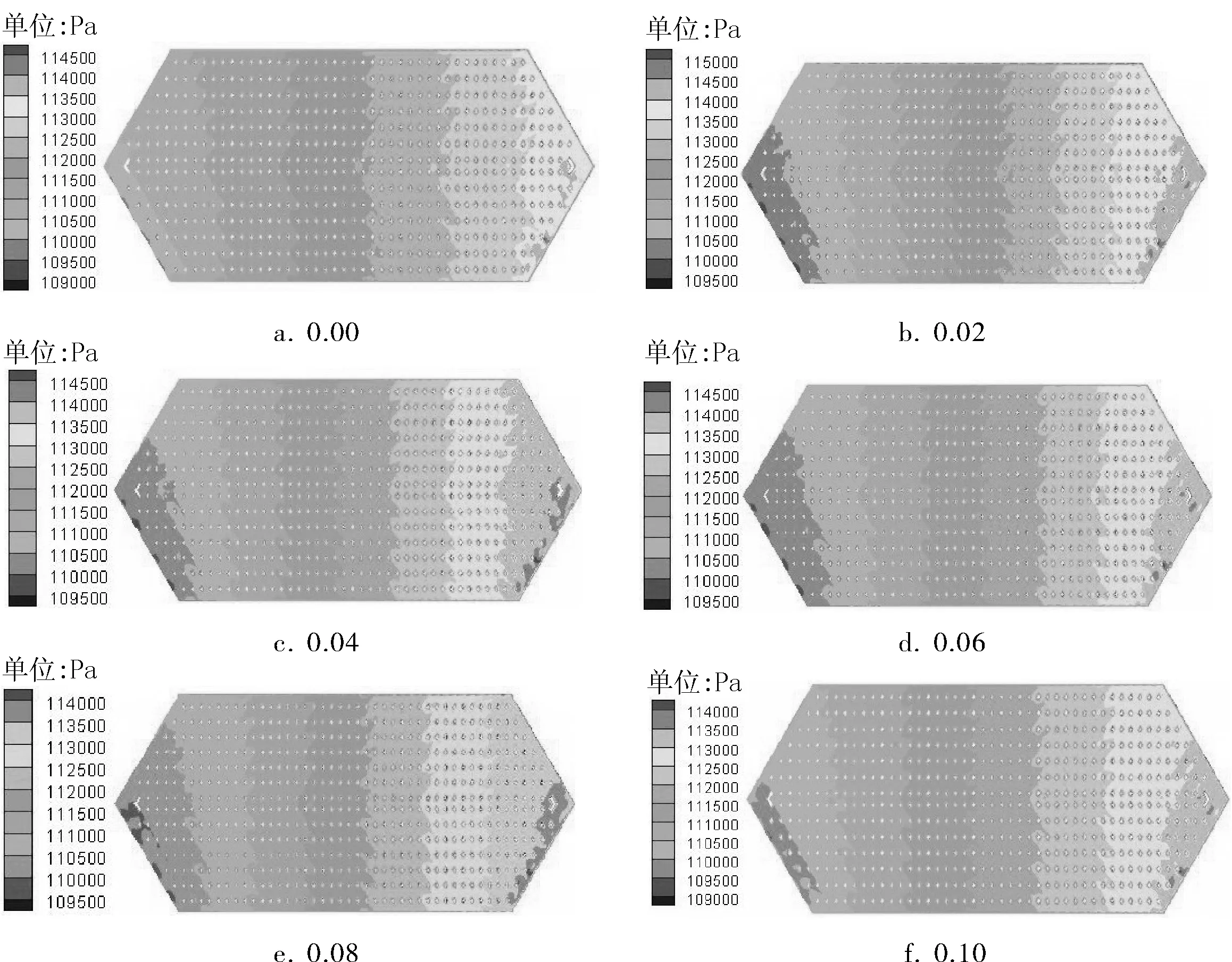
图5 冷流道中单相和两相冷流道压力分布

图6为冷流道中单相和气液两相流动时的水温分布图，温度的分布与速度和压力的分布密切相关，结合图4、5，速度较高、压力梯度较大的位置，温度梯度也相对较大。水的温度沿着流动方向逐渐升高，这是由于水进入换热器后，不断与热水通过板片进行换热，左上端是高温区，对流换热量较大，所以沿宽度方向的温度梯度较大，同时对比各图可以看到，随着含气率的增大，右下侧换热死区位置的气体增多，流体的流速比主流区的流速大，流体的湍动增强，低温温度区域明显减小，说明在一定含气率范围内，随着气体含气率的增大，可以使换热死区的换热得到明显改善。

图6 冷流道中单相和两相流动时水的温度分布

2.3 相关模拟结果

图7、8为气泡直径1mm，空气体积含气率不同时，冷流道努塞尔数Nu和压降Δp随雷诺数的变化关系。由图7可以看出，冷流道的努塞尔数Nu随两相流体雷诺数Re的增大而增大，但增大的趋势逐渐减小，并且随着空气体积含气率的增大，冷流道努塞尔数也随之增大；由图8可以看出，冷流道压降随两相流体雷诺数Re的增大而增大，并且增大的趋势越来越明显，并且随着空气体积含气率的增大，压降随之减小。因此从两图的结果可以得到，随着空气体积含气率的增大，改善了冷热流体的换热状况，降低了压降损失，即增强了换热器的换热效果。

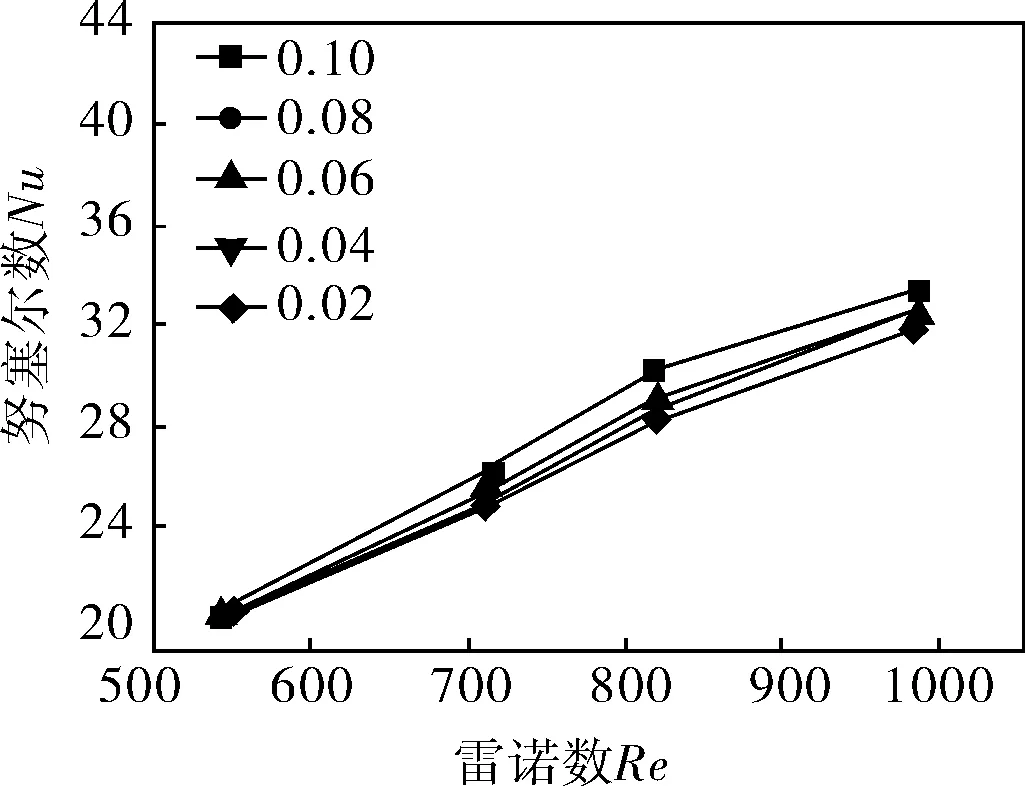
图7 不同空气体积含气率时冷流道努塞尔数和雷诺数的关系

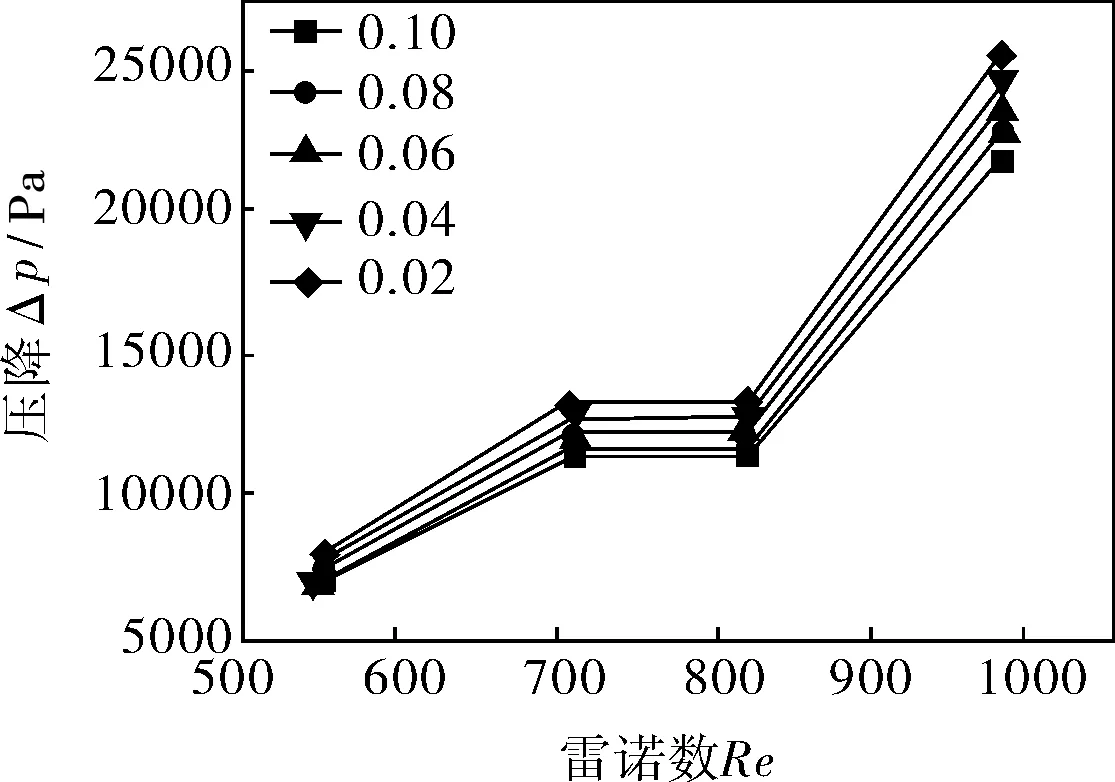
图8 不同空气体积含气率时冷流道压降和雷诺数的关系

3 结束语

笔者对人字形板式换热器中气液两相流的温度场、压力场、速度场以及气体的分布进行了数值模拟，通过分析可知：不同空气体积含气率的气液两相流在板式换热器中流动时，冷流道的压降和努赛尔数均随着雷诺数的增大而增大，并且随着空气体积含气率的增大，换热效果增强；在进出口连线一侧的气体体积分数比另一侧大，并且随着含气率增大，流道内的气体分布趋于均匀，换热死区位置的气体增多，增强了该处流体的扰动，使换热死区的换热特性得到了明显改善。

[1] 王志春,张文景,李文涛.基于ANSYS的一种气液两相流流量测量传感器的仿真研究[J].化工自动化及仪表,2011,38(1):48～51.

[2] 李英，陈光文，袁权.微通道内液-液两相流研究进展[J].化工进展，2013，32(8)：1743～1748.

[3] 付涛涛.微通道内气液两相流及气泡行为研究[D].天津：天津大学，2009.

[4] 赵楠.垂直入口微通道内气液两相流模拟研究[D].北京：北京交通大学，2010.

[5] Masuo Kaji，Toru Sawai，Yosuke Kagi，et al.Heat Transfer and Fluid Dynamics of Air-Water Two-phase Flow in Micro-channels[J].Experimental Thermal and Fluid Science，2010，34(4)：446～453.

[6] Shiomi Y， Nakamishi S， Uehara T.Characteristics of Two-phase Flow in a Channel Formed by Chevron Type Plates[J]. Experimental Thermal and Fluid Science，2004，28(2/3)：231～235.

[7] Nilpueng K，Wongwises S.Two-phase Gas-Liquid Flow Characteristics Inside a Plate Heat Exchanger[J]. Experimental Thermal and Fluid Science，2010，34(8)：1217～1229.

[8] Vlasogiannis P， Karagiannis G， Argyropoulos P，et al.Air-Water two-Phase Flow and Heat Transfer in Plate Heat Exchanger[J].International Journal of Multiphase Flow，2002，28(5)：757～772.

[9] 徐志明，王月明，张仲彬.板式换热器性能的数值模拟[J].动力工程学报，2011，31(3)：198～202.