枝状管网布局优化中的3类问题
商冠琪
(中国石油化工股份有限公司)
目前,针对集输管网的优化设计问题多采用分级优化的策略,根据不同的管网形态将系统优化分为多个子问题来处理,比如,星枝管网的优化设计[1],通过分级优化将气田星枝状地面集输系统优化分为井组最优划分、星式管网布局优化、干支管网布局优化和管网参数优化4个子问题进行研究。干支管网布局优化是进行站点位置的合理布置,可分为3方面的内容,一是无向图枝状结构,二是枝状结构中心点,三是有向图的枝状连接。
1 无向枝状结构连接
无向枝状结构连接关系,多采用图论的最小生成树算法确定无向图的连接关系。根据图论的知识,管网中的站点和管段可以抽象为图中的节点和边,对于任意两个节点间,理论上都可能存在一条管线相连,任意两点存在边则构成了一个完备图。n个节点的完备图存在Cn2=n(n-1)/2条边,在这些边中,选择n-1条边就可以得到枝状管网的连接方式,而这n-1条管线也就构成了这个完备图的一棵生成树。一个完备图的生成树有很多,可能的枝状管网的连接方式也就有很多,没有考虑到流向的问题,可将枝状管网连接方式的优化问题转变成求无向图中的最小生成树问题。
1.1 模型的建立
求解无向图最小生成树的数学模型为:
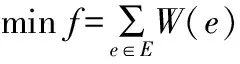
(1)
式中E——图中所有边的集合;
W(e)——边e的权值。
在求解最小生成树时,不仅要使枝状管网的管线总长度最短,还要考虑各节点气量不同而造成的管径差异,但是流向未知,可对顶点加权,得到求解枝状管网最优连接方式的数学模型如下:
(2)
其约束条件为:
(3)
(4)
(5)
Aij=0,1
(6)
式中Aij——0~1决策变量,当节点i、j间有管线连接时,Aij为1,当节点i与j不相连时,Aij为0;
Lij——第i节点到第j节点间的管线长度;
m——节点的总数;
qi——第i节点的集气量。
1.2 求解算法
求解算法主要包括Kruskai、 Prim和SI生成树算法。这3种方法是图论中的经典算法,算法运行稳定,是集输系统枝状结构布局普遍采用的方式。
Prime算法的时间复杂度为O(n2),n为图中顶点的个数,由于Prime算法与边的数目无关,适合求解边稠密的网络图的最小生成树;Kruskal算法的时间复杂度为O(lg2k+2klg2n+n),n为顶点个数,k为边的个数,由于Kruskal算法的时间复杂度主要取决于边的数目,适合求解边稀疏的网络图的最小生成树;SI算法在管网结构中加入了额外点,其优化结果优于其他两种算法,但运行效率不高。
学者李书文首次对3种算法在枝状管网布局优化研究中进行了论述[2];康正凌和袁宗明采用Kruskai算法确定枝状管网连接关系[3];李征用Prim算法确定枝状天然气管网连接关系[4];郑清高等都采用了SI算法来确定气田集输管网最优网络布局[5~7]。
2 枝状结构中心点的确定
枝状结构中心点问题是在确定了枝状结构连接关系时,在给定的生成树结构中选取合理节点作为站点。中心点作为整个枝状管网系统的中心,它的位置决定了干支管网各管段流量的流向和分布,从而直接影响到枝状管网中集气管线直径和长度的变化。中心点选址问题就可以转化为图论中求解连通图的加权中心问题,即选择连通图的某个顶点,使得其他所有顶点到该顶点的距离和最小,则该顶点就称为此连通图的加权中心,也就是优化确定的中心站点位置。
2.1 模型的建立
在连通图中,从一个顶点到另一个顶点间的加权路径最短,要找到这条途径,在图论中称为最短路径问题。若整个管网有m个节点,分别对每个节点到其他所有节点之间求解最短路径,并将各个最短路径求和,最小值对应的节点即为中心节点位置。
对于节点j至i的加权距离,计算式为:
(7)
则求解中心节点的目标函数为:
(8)
其中,qj为节点j的集气量。
2.2 求解算法
计算任意两顶点之间的最短路径,在图论中应用较普遍的有Dijkstra算法及Floyd算法等。
Dijkstra算法又叫做标号法,应用一次的时间复杂度为O(m2),它每次只能求出图中一个特定顶点到其他各顶点的最短路,如果要计算像煤层气集输管网这种具有m个顶点的无向图中任意两个顶点间的最短路径,需要将图中每一个顶点依次视为起始点,然后反复应用Dijkstra算法计算。因此,应用Dijkstra算法求解该问题的时间复杂度为O(m3)。
Floyd算法又叫做插点法,在计算时从任意一条单边路径开始,对于每一对顶点u和v,看是否存在一个顶点w使得从u到w再到v比己知路径的加权距离更短,如果存在就更新它,如此循环,直到得出最短路径。Floyd算法求解该问题最短路径的时间复杂性也是O(m3)。
徐国栋和梁政针对海上边际油田和陆上气田,研究了枝状管网的中心站址选择问题[8]。
3 有向枝状连接结构布置
有向枝状结构连接关系。把无向树转化为有向树后,在无向图中确定的连接方式,不一定是有向图的最优连接方式,所得到的管网最小流量长度和也不一定是有向树的最小流量长度和。从数学模型来看,有向图布局优化的数学模型与无向图相同,但优化算法来看,徐国栋和梁政首先采用了无向枝状结构连接确定连接关系,然后确定管网的中心点,在此基础上一管网的流量长度之和最小原则,调整中心站的位置,最终确定枝状管网的布局[8]。陈坤明等采用单亲遗传算和深度优先搜索混合算法对该问题进行了求解[9]。有向图枝状连接结构布置,由于问题的复制性,目前无较成熟和被广泛认可的求解方法。
4 结束语
枝状管网作为集输系统普遍采用的结构之一,将管网布局转变为无向枝状布局和中心点位置优化问题是当前优化设计普遍采用的方式,其优化算法简便且稳定,已得到广泛应用。但集输系统枝状结构布局优化区别于一般图的连接关系是管道中流体的存在,在布局优化设计方案中考虑流体方向,也是枝状管网布局研究的难点。无向连接关系布局是对此问题的简化处理,优化结果无法保证最优性。目前虽有学者对此问题进行了研究,但效果有待提高,需研究者继续努力。
[1] 潘红丽,杨鸿雁.气田地面集输管网系统的优化设计[J]. 油气储运,2002,21(4):14~18.
[2] 李书文.气田网络优化布局初探[J].天然气工业,1989,9(5):68~72.
[3] 康正凌,袁宗明.树枝状天然气管网优化设计[J].天然气工业,2001,21(3):76~78,2.
[4] 李征.天然气集输管网优化设计方法研究[J].内蒙古石油化工,2009,34(6):19~21.
[5] 郑清高.油气集输管网几何布局的研究[J].石油学报,1995,(1):139~143.
[6] 孟荣章,李书文,汤林.大型气田集输管网布局优化[J].石油规划设计,1998,9(2):20~22,4.
[7] 姚麟昱,骆彬,孟庆华,等.川西高压高产气田集输管网规划设计[J].石油规划设计,2010,21(6):21~24,54.
[8] 徐国栋,梁政.气田集输管网布局优化研究[J].石油规划设计,2004,15(6):18~21.
[9] 陈坤明,简朝阳,刘松泉,等.单亲遗传和深度优先搜索算法的集输管网优化[J].油气田地面工程,2012,31(8):34~35.

