一种基于正则化的边缘定向插值算法
季成涛 何小海 符耀庆 梁子飞 卿粼波
一种基于正则化的边缘定向插值算法
季成涛①何小海*①符耀庆②梁子飞①卿粼波①
①(四川大学电子信息学院 成都 610065)②(中海油能源发展股份有限公司北京分公司 北京 100027)
针对传统的基于线性回归模型插值算法不能对变化剧烈的边缘进行有效插值的问题,该文提出一种基于正则化的边缘定向插值算法。算法主要分为两部分:参数估计部分与数据估计部分。在参数估计部分,为了更加准确地描述图像局部结构,把已估计的高分辨率像素作为训练像素的一部分,用以进行回归模型参数的估计。在数据估计部分,引入像素平滑方向作为正则化项,以降低参数的误估计引起的数据估计偏差。实验结果表明,该算法能很好地保持图像的边缘特征,尤其在变化比较剧烈的边缘区域;与双三次插值算法及基于正则化的局部线性回归插值算法(Regularized Local Linear Regression, RLLR)相比,该算法能取得更好的视觉效果及较高的PSNR值。
图像处理;插值;回归模型;训练像素;正则化
1 引言
图像插值,是对已知的低分辨率(Low Resolution, LR)图像通过一定的算法获得高分辨率(High Resolution, HR)图像的过程。图像插值在很多领域得到了广泛的应用,如消费电子设备、计算机视觉、遥感技术应用、医学图像处理等。传统的图像插值算法有最近邻插值、双线性插值、双三次插值等[1,2],这些插值方法的优点是计算简单,运行时间少,但由于这些算法的插值滤波器有着各向同性的特点,不能根据不同的图像结构进行自适应插值,导致插值后的边缘部分出现如模糊、振铃、锯齿等明显的人工处理痕迹。
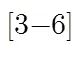
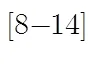
以上基于线性回归模型的插值算法虽然取得了较好的效果,但对边缘两侧变化较剧烈的部分,其插值效果并没有得到很好的改善。究其原因主要是在模型估计阶段利用低分辨率像素估计的线性回归模型参数,并不能完全适合高分辨图像的结构,本文针对这一问题进行了改进。在模型参数估计阶段,把低分辨率像素和已经估计的高分辨率像素作为训练像素进行参数的估计,另外,引入了像素平滑方向作为正则化项,以降低插值窗口内结构的多变所带来的插值误差。
2 图像自回归模型
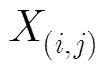

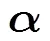
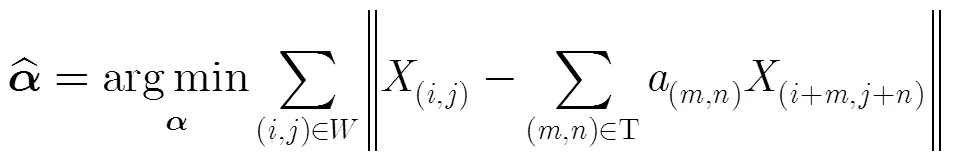
其中为固定大小的局部窗口。
3 本文算法
通常,在以未知像素为中心的局部窗口内进行参数估计后,就可以利用式(1)进行未知像素的插值,如图1所示。实验显示,在平滑区域及两侧变化不大的边缘这样做会产生较好的插值效果。但对于两侧变化剧烈的边缘而言,参数估计会因为图像结构的多变导致误估计,本文针对该问题进行了改进。首先在参数估计阶段,将已知的低分辨率像素和已经估计出的高分辨率像素作为训练像素,以降低由于分辨率不同而引起的参数估计误差;在数据估计阶段,首先估计出以待插值像素为中心的像素平滑方向,然后将利用平滑方向的像素估计出的像素值作为正则化项,以降低由于图像结构多变导致的插值误差。综上所述,可用式(3)进行对未知像素的求解:
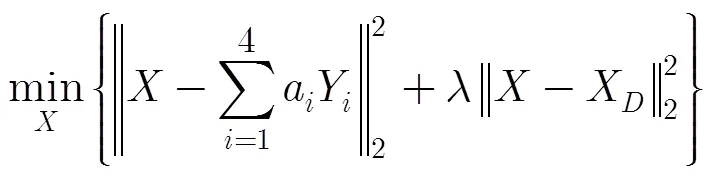
本文采用2遍插值对整幅图像进行插值,如图1所示,其中图中黑色实心点为已知的低分辨率像素,白色点是第1遍插值操作的像素,灰色点是第2遍插值操作的像素。本文对边界采样用双三次插值算法进行处理。下文以第1遍插值过程为例说明算法流程,算法流程图如图2所示。

图1 基于线性回归模型插值示意图
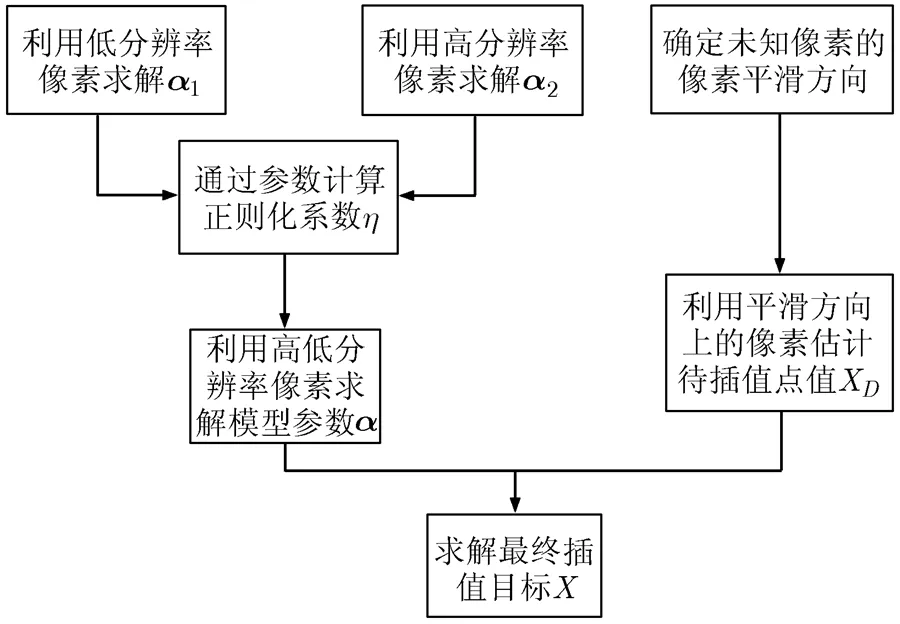
图2 本文算法流程图
3.1 模型参数估计



对式(4)进行求解得到
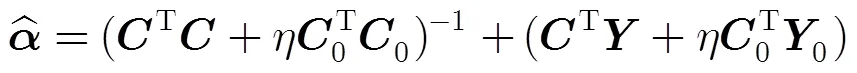

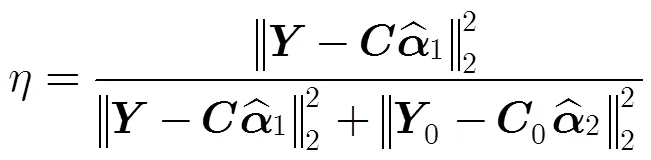
3.2 数据估计
在参数估计阶段,假定插值窗口内的图像结构都服从同一参数模型,然而对于两侧变化比较剧烈的边缘来说,由于结构的多变不能很好地用同一参数模型进行描述,因而会产生较大误差;为了克服图像结构多变引起的边缘插值不准确,本文引入了像素平滑方向作为正则化项,以使最终的插值结构更能适应图像的局部结构。
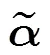
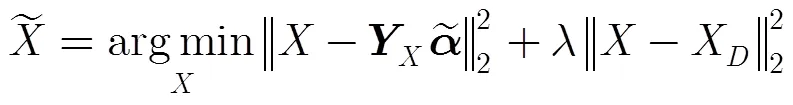
4 实验结果
为了评价本文算法的效果,本文选取了KODAK 图像库中的图像作为测试图像。首先对原始的高分辨率图像进行以2为因子的隔点下采样,将得到的对应的低分辨率图像作为输入图像,然后用本文算法进行插值处理。同时将本文的插值效果与双三次插值算法和RLLR插值算法进行了对比,对应的PSNR值如表1所示。
表1实验重建结果衡量标准PSNR对比
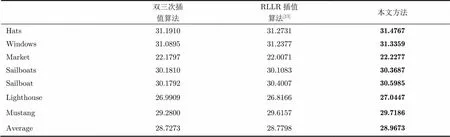
双三次插值算法RLLR插值算法[11]本文方法 Hats31.191031.273131.4767 Windows31.089531.237731.3359 Market22.179722.007122.2277 Sailboats30.181030.108330.3687 Sailboat30.179230.400730.5985 Lighthouse26.990926.816627.0447 Mustang29.280029.615729.7186 Average28.727328.779828.9673
对于彩色图像,是将彩色图像的3个通道当成3幅灰度图像分别进行插值,最后将各通道的插值结果合并成彩色图像。图5是用3种算法对灰度图像进行处理的实验结果,图6是用3种算法对彩色图像处理的实验结果。
从实验结果可以看到,双三次插值与RLLR插值算法在进行边缘插值时,存在较严重的锯齿和不平滑现象,如图5中的白色线条和灰色线条,图6中的白色直线处都出现了较明显的锯齿效应,本文算法能更好地保护图像的边缘部分。

图5 灰度图像插值结果

图6 彩色图像插值结果
5 结论
传统的基于线性回归模型的插值算法主要存在以下两个问题:由于分辨率不同引入的参数估计误差和由于局部图像结构多变引入的数据估计误差。针对这两个问题本文提出了一种基于正则化的边缘定向图像插值算法。为了克服分辨率不同所引入的误差,本文在参数估计阶段,同时把低分辨率像素与已经估计的高分辨率像素作为训练像素进行模型参数估计。在数据估计阶段,通过引入像素平滑方向作为正则化项,用来克服图像结构多变所带来的误差。实验结果表明,本文算法取得了较好的视觉效果和较高的PSNR值,尤其在边缘两侧变化剧烈的部分能更好地保护边缘。
[1] Keys R C. Cubic convolution interpolation for digital image processing[J].,,, 1981, 29(6): 1153-1160.
[2] Hou H S and Andrews H C. Cubic splines for image interpolation and digital filtering[J].,,, 1978, 26(6): 508-517.
[3] Dong Wei-sheng, Zhang Lei, Shi Guang-ming,.. Nonlocal back-projection for adaptive image enlargement[C]. 16th IEEE International Conference on Image Processing (ICIP), Cairo, 2009: 349-352.
[4] Hung Kwok-wai and Siu Wan-chi. Single image super- resolution using iterative wiener filter[C]. IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Kyoto, 2012: 1269-1272.
[5] Guo Kai, Yang Xiao-kang, Zha Hong-yuan,.. Multiscale semilocal interpolation with antialising[J]., 2012, 21(2): 615-625.
[6] 赵旦峰, 王博, 杨大伟. 一种边缘定向平滑图像插值算法[J]. 电子与信息学报, 2012, 34(7): 1543-1546.
Zhao Dan-feng, Wang Bo, and Yang Da-wei. An edge- directed smoothness algorithm for image interpolation[J].&, 2012, 34(7): 1543-1546.
[7] Zhang Lei and Wu Xiao-lin. An edge-guided image interpolation algorithm via directional filtering and data fusion[J]., 2006, 15(8): 2226-2238.
[8] Li Xin and Orchard M T. New edge-directed interpolation[J]., 2001, 10(10): 1521-1527.
[9] Asuni N and Giachetti A. Accuracy improvements and artifacts removal in edge based image interpolation[C]. Proceedings of the Third International Conference on Computer Vision Theory and Applications (VISAPP), Funchal, 2008: 58-65.
[10] Zhang Xiang-jun and Wu Xiao-lin. Image inerpolation by adaptive 2-D autoregressive modeling and soft-decision estimation[J]., 2008, 17(6): 887-896.
[11] Liu Xian-ming, Zhao De-bin, Xiong Rui-qin,.. Image interpolation via regularized local linear regression[J]., 2011, 20(12): 3455-3469.
[12] 任杰, 刘家瑛, 白蔚, 等. 基于隐式分段自回归模型的图像插值算法[J]. 软件学报, 2012, 23(5): 1248-1259.
Ren Jie, Liu Jia-ying, Bai Wei,.. Image interpolation algorithm based on implicit piecewise autoregressive[J]., 2012, 23(5): 1248-1259.
[13] Hung Kwok-Wai and Siu Wan-Chi. Robust soft-decision interpolation using weighted least squares[J]., 2012, 21(3): 1061-1069.
[14] Tang K, Oscar C Au,and Fang Lu. Image interpolation using autoregressive model and gauss-seidel optimization[C]. 6th IEEE International Conference on Image and Graphics (ICIG), Hefei, China, 2011: 66-69.
[15] Tomasi C and Manduchi R. Bilateral filtering for gray and color images[C]. Proceedings of the Sixth International Conference on Computer Vision (ICCV), Bombay, 1988: 839-846.
季成涛: 男,1988年生,硕士生,研究方向为图像处理、图像超分辨率等.
何小海: 男,1964年生,教授,博士生导师,研究方向为图像处理、数字通信等.
符耀庆: 男,1962年生,高级工程师,研究方向为计算机应用技术及图像处理.
梁子飞: 男,1989年生,博士生,研究方向为图像处理、图像超分辨率等.
卿粼波: 男,1982年生,博士,讲师,研究方向为图像处理、图像通信.
An Edge Directed Interpolation Algorithm Based on Regularization
Ji Cheng-tao①He Xiao-hai①Fu Yao-qing②Liang Zi-fei①Qing Lin-bo①
①(,,610065,)②(&,100027,)
The traditional methods based on linear regression model preserve the edge in some degree, but hardly work on the sharp edge. To solve this problem, an edge directed interpolation algorithm based on regularization is proposed in this paper, which is composed of the parameters estimation part and the data estimation part. In the first part, the high resolution structures which have been estimated are taken as one part of the training pixel to estimate the parameters of the linear regression model for effectively describing the structure. In the second part, the smooth pixel’s direction is applied as the regularization to reduce the error of estimated data aroused from the incorrect parameters. Experimented results show that the proposed method preserves the edge of image effectively, and both the visual effects and the PSNR are all better than bi-cubic and Regularized Local Linear Regression (RLLR).
Image processing; Interpolation; Regression model; Training pixel; Regularization
TN911.73
A
1009-5896(2014)02-0293-05
10.3724/SP.J.1146.2013.00582
何小海 hxh@scu.edu.cn
2013-04-25收到,2013-07-27改回
国家自然科学基金(61071161),国家自然科学基金委员会和中国工程物理研究院联合基金(11176018)资助课题

