Duffing振子在低信噪比雷达目标微动特征提取中的应用
邓冬虎 张 群 罗 迎 姚 赛 李宏伟
Duffing振子在低信噪比雷达目标微动特征提取中的应用
邓冬虎*①张 群①罗 迎①姚 赛②李宏伟①
①(空军工程大学信息与导航学院 西安 710077)②(海军工程大学电子工程学院 武汉 430033)
雷达目标部件的旋转运动引起的微多普勒效应为目标精确识别提供了新的技术途径,近年来获得了广泛研究。该文以含旋转部件目标为例,提出了一种利用Duffing振子在低信噪比条件下提取雷达目标微动特征的方法。由于经参考信号共轭相乘后的旋转散射点回波信号是由多个正弦分量组成的,因此采用Duffing振子系统对回波信号中的正弦分量进行检测,并对该正弦分量频率所对应的距离单元在距离-慢时间平面上进行能量增强,最后结合Hough变换完成对雷达目标微动特征的提取。仿真实验验证了该方法的有效性。
逆合成孔径雷达(ISAR);微动特征提取;旋转部件;Duffing振子
1引言
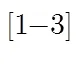
但是,在利用逆合成孔径雷达(Inverse SAR, ISAR)来对含有微动部件的地面目标、低空飞行目标或海面目标进行微动特征提取时,回波信号中往往会存在大量的地杂波或海杂波等背景噪声[8,9]。此外,有些目标的微动部件,如卡车的轮胎,反射系数较小,目标回波信号能量弱。这些都导致雷达工作在低信噪比(Signal-to-Noise Ratio, SNR)条件下,严重影响了目标微动特征提取的准确度。虽然可以采用多次回波相消、空时自适应处理或自适应多通道均衡等传统方法来对噪声进行抑制,进而检测有用信号,但是抑制噪声难免会造成回波信号能量的损失[9]。
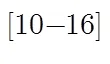
基于此,本文就Duffing混沌振子在低信噪比雷达目标微动特征提取中的应用展开研究。在对宽带雷达系统微多普勒效应分析的基础上,构造参考信号,并与夹杂强噪声的目标回波信号作去斜处理。通过对处理后的信号进行分析得出:对于任意慢时间时刻,经去斜处理后的散射点回波信号均可理解为一时域带限单频信号。利用Duffing振子将淹没在强噪声中的单频信号检测出来,并对其相应的距离单元进行能量增强,可将距离-慢时间单元平面上的微动所形成的正弦曲线凸显出来,然后利用Hough变换完成对雷达目标微动特征的提取。
2 宽带雷达系统微多普勒效应分析
假设雷达发射信号为
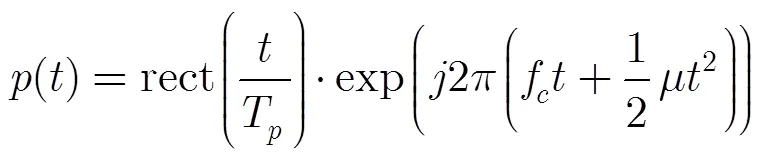
其中为矩形窗函数,其值只有在 时为1,在快时间取其它值时为0。是载频,是脉冲宽度,是调频率。


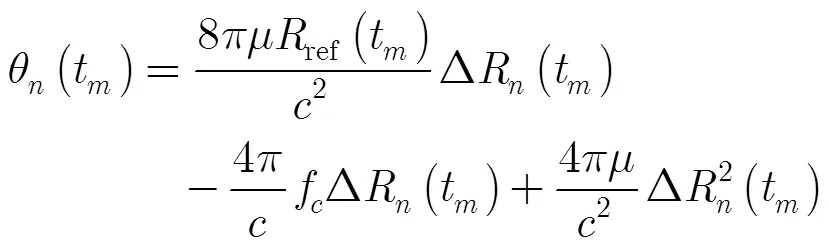
且
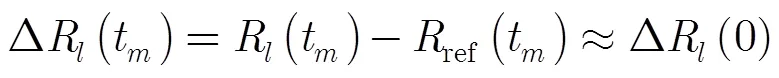

3 基于Duffing混沌振子的正弦信号频率提取
改进的Holmes型Duffing状态方程为[11]
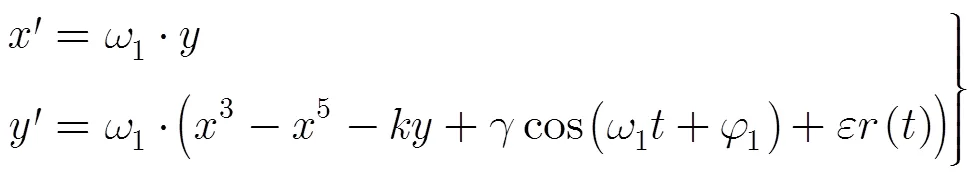
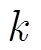
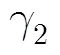
4 Duffing振子在微动特征提取中的应用
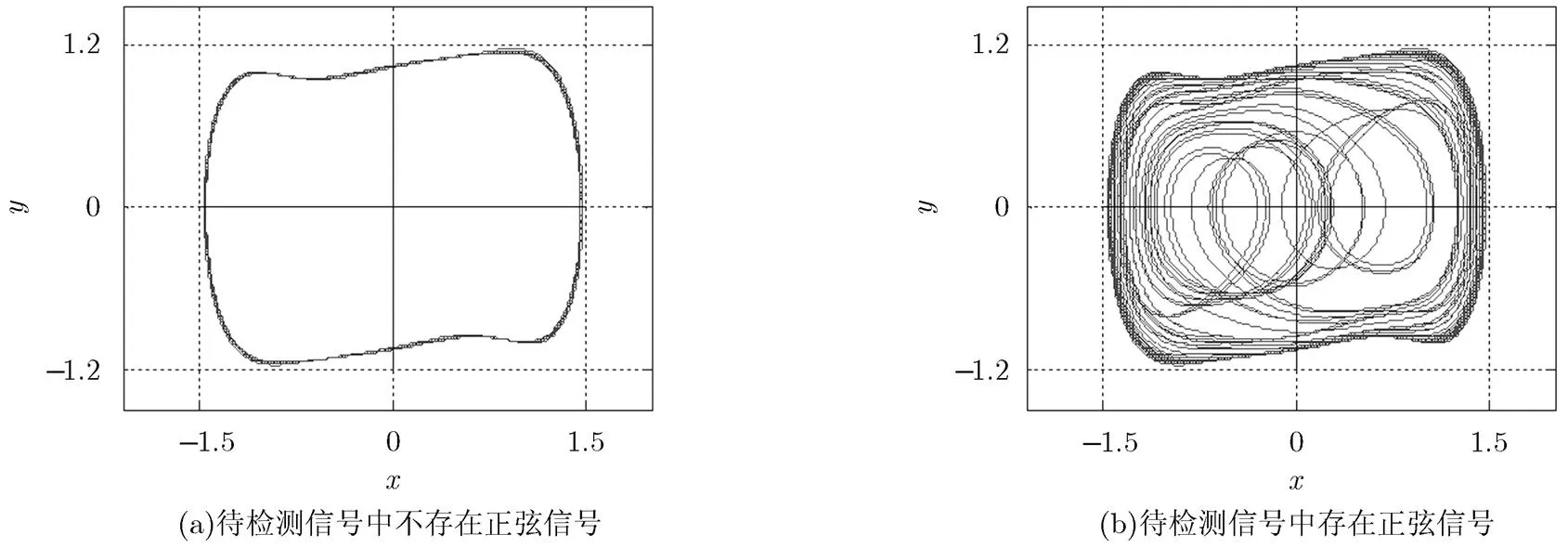
图2 待检测信号中是否存在正弦信号时的相轨迹图
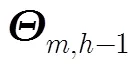
(3)对每个脉冲都重复步骤(2),直到对所有脉冲信号都检测完毕。
以上论述主要是针对旋转形式的微动特征提取方法。事实上,由于振动所产生的回波信号形式与旋转近似,因此采用本文方法也可以实现振动形式的微动特征提取。
5 仿真分析
5.1 正弦信号频率检测仿真与分析
从图3中可以看到,利用Duffing振子不能100%地完成对正弦信号的检测,这主要是因为Duffing振子相轨迹状态对噪声具有免疫力的结论是从统计意义上得出的[13]。但是,在-45 dB的信噪比条件下,系统的检测概率仍在93%以上,而虚警概率则在2.2%以内。因此,利用Duffing振子可以较好地完成对低信噪比条件下的正弦信号检测。
表1仿真中采用的正弦信号频率及参考信号幅值

信号频率(MHz)参考信号幅值信号频率(MHz)参考信号幅值 18.00.71476821.00.714888 19.00.71480522.00.714938 20.00.714847
5.2 微动特征提取仿真与分析
图5为无噪声条件下经去斜处理后回波信号的距离-慢时间平面。从图5中可以看出,信号的距离-慢时间平面图为旋转点所产生的正弦曲线谱与非旋转点所产生的直线谱的叠加。图6给出了SNR= -30 dB时的距离-慢时间平面(信噪比定义为时域中经去斜处理后信号与噪声的平均功率比)。对比图5和图6,可发现由于噪声的影响,旋转点所产生的正弦曲线谱与非旋转点所产生的直线谱将完全被噪声所淹没。
基于Hough变换的微动特征提取方法就是将旋转散射点在距离-慢时间平面上所呈现出的具有固定频率和幅度的正弦曲线参数提取出来。然而如图6所示,在低信噪比条件下,距离-慢时间平面上正弦曲线完全被噪声所淹没,这极大地影响了Hough变换提取微动特征的准确度。
针对这一问题,采用Duffing振子将淹没在强噪声中的单频信号检测出来,并对其相应的距离单元进行能量增强10倍,可将距离-慢时间单元平面上的微动所形成的正弦曲线凸显出来,结果如图7所示。对比图7和图5可发现,虽然在图7中存在一些虚假点和空白点,这些都是因为利用Duffing振子系统对正弦信号进行检测时存在一定的虚警和漏警,但是从整体上来看,利用Duffing振子系统可有效地完成对目标回波信号中各正弦分量的检测。此后再利用Hough变换在图7平面上对微动特征进行提取。

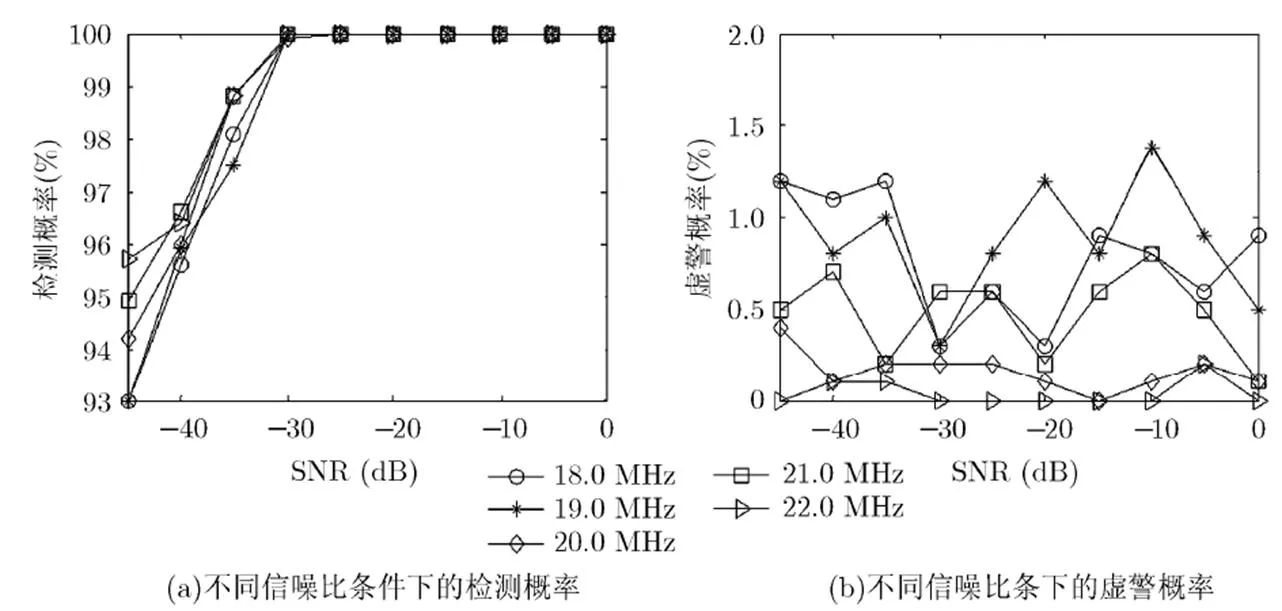
图3 检测不同频率信号仿真

图4 含旋转点部件目标散射点模型图

图5 无噪声时距离-慢时间平面

图6 SNR=-30 dB时距离-慢时间平面

图7 能量增强后的距离-慢时间平面
表2是否结合Duffing振子系统微动特征提取结果

结合Duffing振子系统不结合Duffing振子系统 旋转点1的微动特征(6 Hz, 5 m, 0 rad)(4 Hz, 5 m, 0 rad) 旋转点2的微动特征(30 Hz, 1 m, 0 rad)(25 Hz, 1 m, 0.8 rad)
6 结束语
雷达目标微动特征的提取已成为当前目标分类和识别领域研究的一个热点。本文提出了一种Duffing振子系统在低信噪比条件下的雷达目标微动特征提取方法,可准确地获得旋转点旋转半径、频率和初始相位信息,适用于微动幅度超过多个宽带雷达的距离分辨单元的应用场景。文中详细描述了该方法实现步骤,并通过仿真实验,验证了采用该方法在-30 dB信噪比条件下能够有效地提取目标的微动特征。
应该指出的是,论文中为了表述清晰,假设运动补偿已经完成,但是由于信噪比较低,这一假设前提实际上是难以实现的。然而是否能够进行理想的运动补偿,并不会对Duffing振子检测正弦信号产生影响,因为我们是在距离向进行正弦信号检测。所以,在距离-慢时间平面上对正弦信号频率对应的距离单元能量增强后,再进行运动补偿也是可行的。此外,由于在相同信号长度下,采样点数越多,信号检测准确性越高,导致所需的采样频率较高。且对于每一个脉冲,本文都需要利用Duffing振子系统来对其中的正弦信号进行检测,导致计算量大。而且对于其它类型的非理想正弦曲线参数的提取,现有的Hough变换可能会存在一些问题。如果曲线谱并不是一个理想的正弦曲线,则需要对Hough变换进行修正,或者采用其它的曲线提取方法。在下一步的工作中,我们将采用实测数据对本文算法进行验证。
[1] Chen V C. Analysis of radar micro-Doppler signature with time-frequency transform[C]. Proceedings of the 10th IEEE Workshop on Statistical Signal and Array Processing, Pocono Manor, PA, 2000: 463-466.
[2] 张群, 罗迎, 何劲. 雷达目标微多普勒效应研究概述[J]. 空军工程大学学报(自然科学版), 2011, 12(2): 23-26.
Zhang Qun, Luo Ying, and He Jin. Review of the researches on micro-Doppler effect of radar targets[J].(), 2011, 12(2): 23-26.
[3] 罗迎, 张群, 王国正, 等. 基于复图像OMP分解的宽带雷达微动特征提取方法[J]. 雷达学报, 2012, 1(4): 361-369.
Luo Ying, Zhang Qun, Wang Guo-zheng,.. Micro-motion signature extraction method for wideband radar based on complex image OMP decomposition[J]., 2012, 1(4): 361-369.
[4] 王宝帅, 杜兰, 刘宏伟, 等. 基于经验模态分解的空中飞机目标分类[J]. 电子与信息学报, 2012, 34(9): 2116-2121.
Wang Bao-shuai, Du Lan, Liu Hong-wei,.. Aircraft classification based on empirical mode decomposition[J].&, 2012, 34(9): 2116-2121.
[5] Ghaleb A, Vignaud L, and Nicolas J M. Micro-Doppler analysis of wheels and pedestrians in ISAR imaging[J]., 2008, 2(3): 301-311.
[6] 艾小锋, 邹小海, 李永祯, 等. 基于时间-距离像分布的锥体目标进动与结构特征提取[J]. 电子与信息学报, 2012, 34(9): 2083-2088.
Ai Xiao-feng, Zou Xiao-hai, Li Yong-zhen,.. Feature extraction of precession and structure of cone-shaped object based on Time-HRRP distribution[J].&, 2012, 34(9): 2083-2088.
[7] 关永胜, 左群声, 刘宏伟, 等. 空间进动目标微动参数估计方法[J]. 电子与信息学报, 2011, 33(10): 2427-2432.
Guan Yong-sheng, Zuo Qun-sheng, Liu Hong-wei,.. Micro-motion parameters estimation of space precession targets[J].&, 2011, 33(10): 2427-2432.
[8] 李强, 张守宏, 张焕颖, 等. 高掠海角下基于Radon 变换的海杂波抑制方法[J]. 电子与信息学报, 2007, 29(5): 1087-1091.
Li Qiang, Zhang Shou-hong, Zhang Huan-ying,.. Method for radon transform based sea clutter suppression at high grazing angles[J].&, 2007, 29(5): 1087-1091.
[9] 邓冬虎, 朱小鹏, 张群, 等. 基于随机共振理论的双基ISAR弱信号提取及成像分析[J]. 电子学报, 2012, 40(9): 1809-1816.
Deng Dong-hu, Zhu Xiao-peng, Zhang Qun,.. The weak signals extraction and imaging analysis in Bi-static ISAR systems based on stochastic resonance[J]., 2012, 40(9): 1809-1816.
[10] 陈新国, 王洁芸. 混沌振子在不同初值下检测弱信号的性能分析[J]. 仪器仪表学报, 2012, 33(12): 2857-2862.
Chen Xin-guo and Wang Jie-yun. Performance analysis of weak signal detection based on chaotic oscillator under different initial condition[J]., 2012, 33(12): 2857-2862.
[11] 刘海波, 吴德伟, 戴传金, 等. 基于Duffing振子的弱正弦信号检测方法研究[J]. 电子学报, 2013, 41(1): 8-12.
Liu Hai-bo, Wu De-wei, Dai Chuan-jin,.. A new weak sinusoidal signal detection method based on Duffing oscillator[J]., 2013, 41(1): 8-12.
[12] 李月, 徐凯, 杨宝俊, 等. 混沌振子系统周期解几何特征量分析与微弱周期信号的定量检测[J]. 物理学报, 2008, 57(6): 3353-3357.
Li Yue, Xu Kai, Yang Bao-jun,.. Analysis of the geometric characteristic quantity of the periodic solutions of the chaotic o scillator system and the quantitative detection of weak periodic signal[J]., 2008, 57(6): 3353-3357.
[13] 朱来普, 张陆勇, 谢文凤. 基于Duffing混沌振子的微弱信号检测研究[J]. 无线电工程, 2012, 42(1): 17-20.
Zhu Lai-pu, Zhang Lu-yong, and Xie Wen-feng,.. Research of weak signal detection based on Duffing chaotic oscillator[J]., 2012, 42(1): 17-20.
[14] Wang Jun-guo, Zhou Jian-zhong, and Peng Bing. Weak signal detection method based on Duffing oscillator[J]., 2009, 38(10): 1662-1668.
[15] Wang Jian-xiong and Hou Chu-lin. A method of weak signal detection based on Duffing oscillator[C]. International Conference on E-Education, E-Business, E-Management and E-Learning, Sanya, 2010: 387-390.
[16] Wang Guan-yu and He Sai-ling. A quantitative study on detection and estimation of weak signals by using chaotic Duffing oscillators[J].:, 2003, 50(7): 945-953.
[17] 罗迎, 池龙, 张群, 等. 用慢时间域积分法实现雷达目标微多普勒信息的提取[J]. 电子与信息学报, 2008, 30(9): 2055-2059.
Luo Ying, Chi Long, Zhang Qun,.. Extraction of micro-Doppler information based on slow-time integration[J].&, 2008, 30(9): 2055-2059.
[18] Zhang Q, Yeo T S, Tan H S,.. Imaging of a moving target with rotating parts based on the hough transform[J]., 2008, 46(1): 291-299.
邓冬虎: 男,1986年生,博士生,研究方向为雷达信号处理.
张 群: 男,1964年生,教授,博士生导师,主要研究方向为雷达信号处理、电子对抗等.
罗 迎: 男,1983年生,讲师,主要研究方向为雷达信号处理.
The Application of Duffing Oscillators to Micro-motion Feature Extraction of Radar Target under Low SNR
Deng Dong-hu①Zhang Qun①Luo Ying①Yao Sai②Li Hong-wei①
①(,,’710077,)②(,,430033,)
The micro-Doppler effect induced by the rotating parts of the target, which provides a new approach for accurate auto radar target recognition, attracts great research attention in recent years. In this paper, taking target with rotating parts for an example, a method for the application of Duffing oscillators to micro-motion feature extraction of radar target under low Signal-to-Noise Ratio (SNR) is proposed. The echo of the rotating parts after multiplying with the conjugate of the reference signal is constructed by several sinusoidal components. Therefore, the Duffing oscillators are used to detect the sinusoidal components of the echo signal. Then, the power of the range cells on the range-slow time plane corresponding to the frequencies of the detected sinusoidal components are enhanced. Finally, the micro-motion feature of the radar target is obtained by the Hough transform. A computer simulation is given to verify the effectiveness of the proposed method.
Inverse SAR (ISAR); Micro-motion signature extraction; Rotating parts; Duffing oscillators
TN957.51
A
1009-5896(2014)02-0453-06
10.3724/SP.J.1146.2013.00624
邓冬虎 dengdonghu@163.com
2013-05-06收到,2013-07-18改回
国家自然科学基金(61172169, 61201369)和陕西省自然科学基金(2011JQ8040)资助课题

