一种三阶多项式相位信号去噪的字典学习算法
欧国建杨士中蒋清平曹海林
一种三阶多项式相位信号去噪的字典学习算法
欧国建*①②杨士中①蒋清平①曹海林①
①(重庆大学飞行器测控与通信教育部重点实验室 重庆 400044)②(重庆电子工程职业学院 重庆 401331)
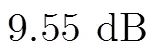
三阶多项式相位信号;递归最小二乘字典学习算法;字典学习;非线性最小二乘法;曲线拟合
1 引言
字典学习算法的研究有3个方向[7]:第1个是基于概率的字典学习方式,如最大后验(MAP)字典学习算法[8];第2个是基于矢量量化的学习方式,如K-means Singular Value Decomposition (K-SVD)字典学习算法[9];最后是基于具体结构的学习方式,如参数字典设计[10]。在这3个研究方向内,涌现出了许多的字典学习算法,其共同特征都是通过某种方式使得字典获得更符合信号内容,特征或者纹理特征。
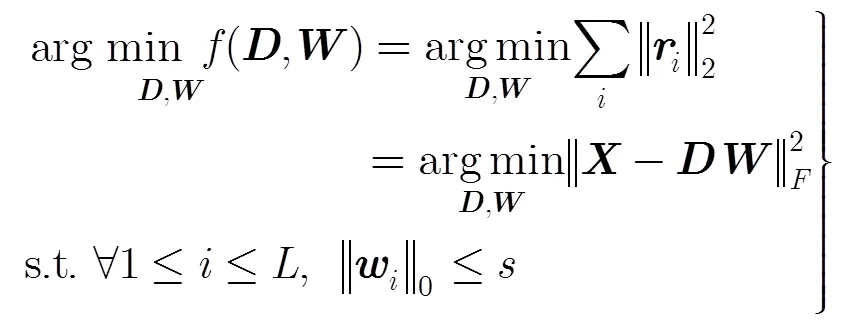
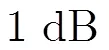
为了实现对信号的有效去噪,本文提出的字典学习算法在RLS-DLA算法的基础上,采用非线性最小二乘法修改了该算法对字典的更新部分,我们称该算法为递归最小均方-非线性最小二乘(Recursive Least Squares- Non Linear Least Squares, RLS-NLLS)字典学习算法。实验表明,相比K-SVD, RLS-DLA和K-SVDD字典学习算法,该算法对CPS具有更好的去噪效果,并且运算量远远低于采用固定字典的形式。
2 问题描述
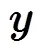
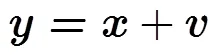
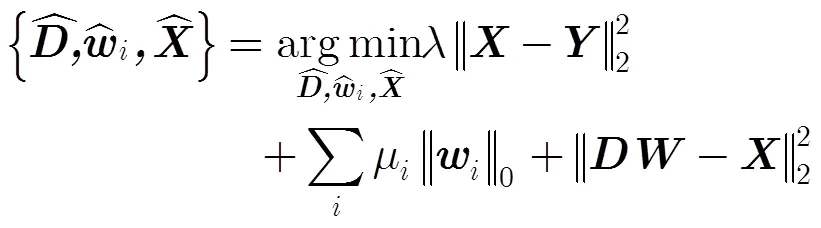
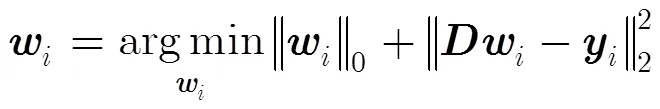
可得到
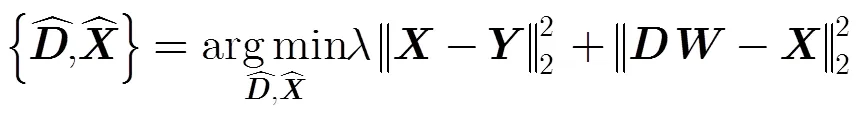
通过对式(5)的求解,可得到
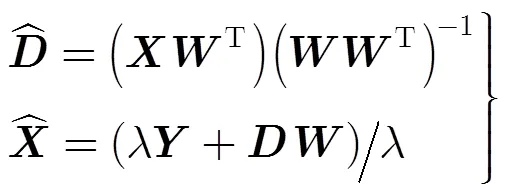
字典学习是从观测信号数据中得到最优的稀疏表示,使得字典中原子结构更接近于观测信号。对有噪声的CPS,通过字典学习,字典中的原子结构必然接近于有噪声的CPS。对此,本文通过非线性最小二乘法对原子结构进行拟合,使其结构接近于无噪声的CPS,这样训练出来的字典通过稀疏表示能有效去除CPS的噪声。
3 算法描述
3.1 算法思想
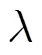
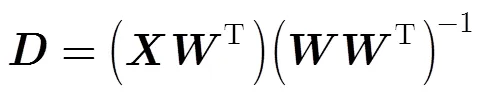
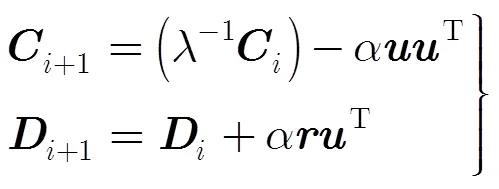
分析RLS-DLA及K-SVD字典学习算法对多项式相位信号去噪效果不好的原因,是因为通过这些字典学习算法训练后得到的字典,其原子结构接近于信号。因此,如果观测信号是带噪声的信号,则通过字典学习,得到的原子结构必然是带噪的信号结构。那么,如果对原子数据进行修正,让原子结构接近与不带噪的信号结构,这样得到的字典通过稀疏表示得到的重构信号,其去噪效果就很明显。于是本文引入了非线性最小二乘法,通过拟合原子数据,让原来带噪的原子结构变为不带噪的原子结构。从图1(a)可以看出,对有加性高斯白噪声的CPS,用RLS-DLA字典学习算法训练字典后,训练后的字典原子是一个含加性高斯白噪声的函数,而从图1(b)中可以看出,通过非线性最小二乘法对原子的拟合,原子是一条光滑的曲线,这样就有效去除了原子的噪声。通过这样的处理得到的字典,通过稀疏分解我们就能对信号有效的去噪。
对非线性最小二乘法拟合,其原理如下:
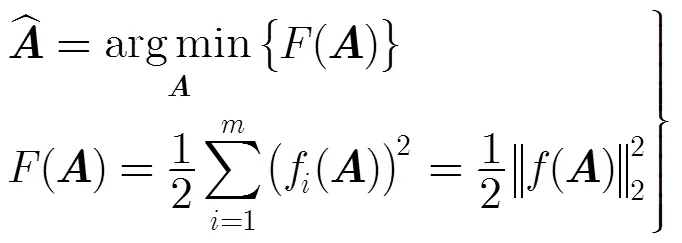
这就是非线性最小二乘法拟合的基本原理。
3.2 . RLS-NLLS算法
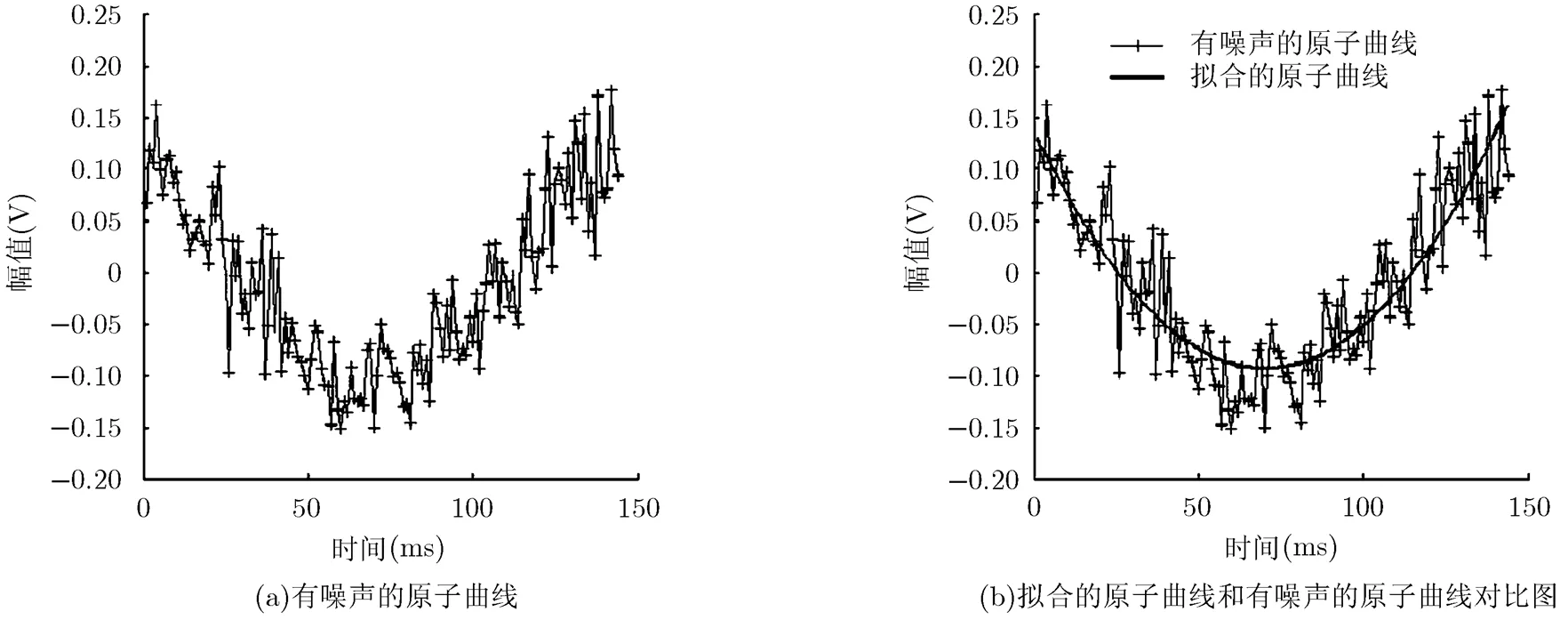
图1 RLS-DLA字典学习算法得到的原子函数曲线及拟合曲线
表1RLS-NLLS算法步骤

任务:找到最好的字典,使得该字典通过稀疏表示能有效地去除CPS的噪声。初始化:任取段观测信号作为初始字典,并使之标准化。(1)取得第个受训信号;(2)通过用追踪算法和,得到系数矢量;(3)求得;(4)运用,计算矢量, ;(5)更新字典。(1)取得字典的第i个原子;(2)运用非线性最小二乘法拟合原子,得到拟合后的原子;(3)把拟合后的原子代替原来的原子;最后得到的字典为。
4 实验
本节主要验证通过该算法对CPS的去噪效果。去噪效果采用信号的均方误差(Mean Square Error, MSE)和信噪比(SNR)来衡量,定义如下:
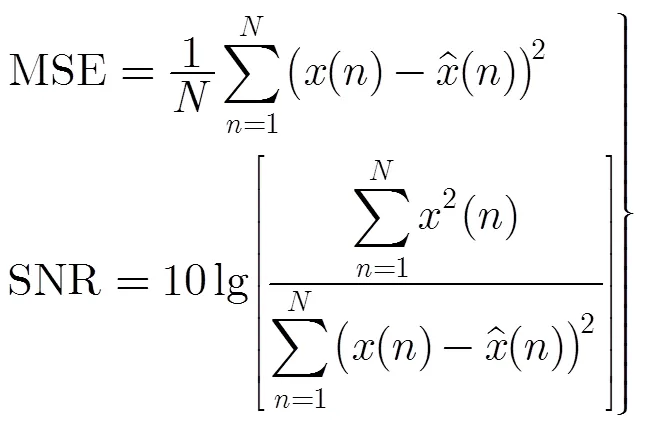
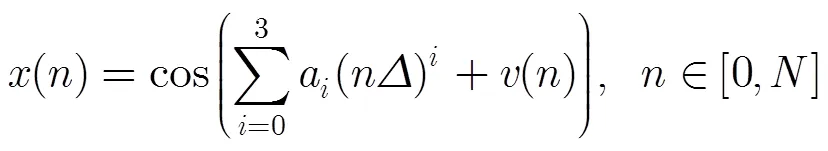
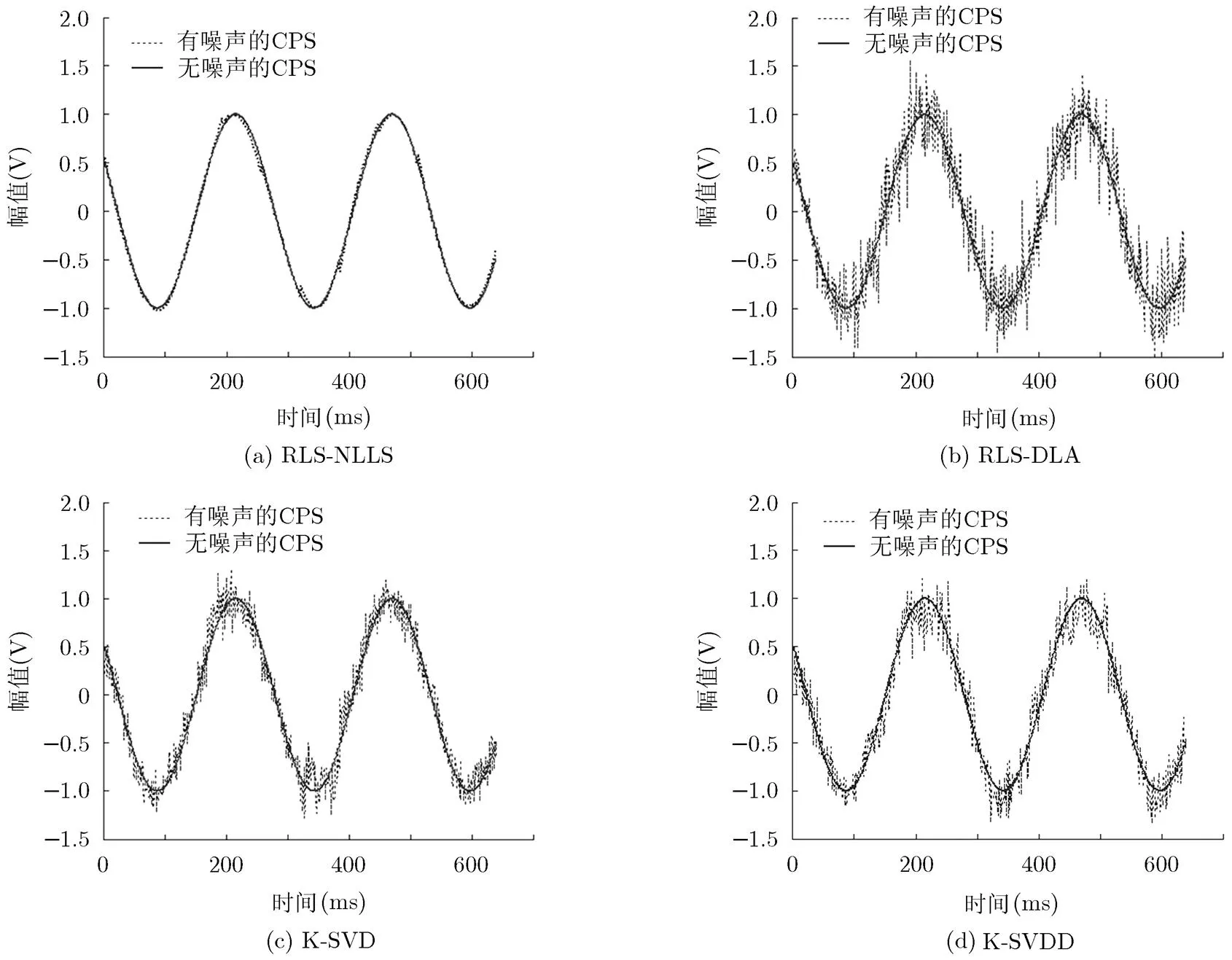
图2 RLS-NLLS, RLS-DLA, K-SVD及K-SVDD重构信号对比图

表2 4种算法重构信号的MSE值
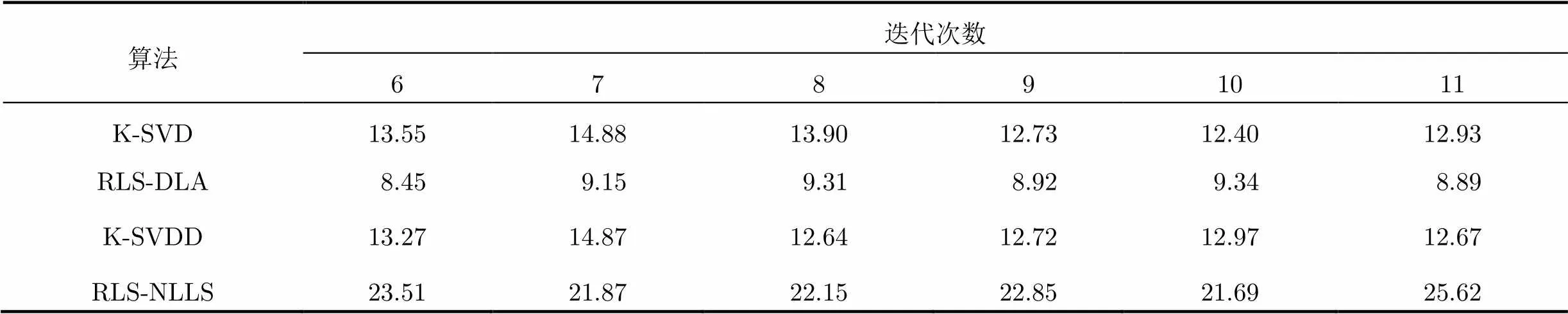
表3 4种算法重构信号的SNR值
5 结论
[1] Djurović I, Djukanović S, Simeunović M,. An efficient joint estimation of wideband polynomial-phase signal parameters and direction-of-arrival in sensor array[J]., 2012, 2012(43): 1-19.
[2] Robby G, McKilliaml I, Vaughan L,.. The asymptotic properties of polynomial phase estimation by least[C]. 2011 IEEE International Conference on,Acoustics, Speech and Signal Processing (ICASSP),Italy, 2011: 3592-3595.
[3] Djukanović S and Djurovicć I. Aliasing detection and resolving in the estimation of polynomial-phase signal parameters[J]., 2012, 92(1): 235-239.
[4] Li Y, Wu R, and Xing M,. Inverse synthetic aperture radar imaging of ship target with complex motion[J].,&, 2008, 2(6): 395-403.
[5] Wang Yong and Jiang Yi-cheng. ISAR imaging of a ship target using product high-order matched-phase transform[J]., 2009, 6(4): 658-661.
[6] Han Ning and Shang Chao-xuan. Fast variable matrix algorithm for sparse decomposition based on PSO[J]., 2012, 34(1): 46-49
[7] Tošic I and Frossard P. Dictionary learning[J]., 2011, 28(2): 27-38.
[8] Ereutz-Delgado K, Murray B J, Rao K,.. Dictionary learning algorithms for sparse representation[J].2003, 15(2): 349-396.
[9] Abaron M, Elad M, and Bruckstein. A. K-SVD: an algorithm for designing overcomplete dictionaries for sparse representation[J]., 2006, 54(11): 4311-4322.
[10] Yaghoobi M, Daudet L, and Davies M E. Parametric dictionary design for sparse coding[J]., 2009, 57(12): 4800-4810.
[11] Skretting K and Engan K. Recursive least squares dictionary learning algorithm[J]., 2010, 58(4): 2121-2130.
[12] Elad M and Abaron M. Image denoising via sparse and redundant representations over learned dictionaries[J]., 2006, 15(12): 3736-3745.
[13] Liu J, Tai X, Huang H,.. A weighted dictionary learning model for denoising images corrupted by mixed noise[J]., 2013, 22(3): 1108-1120.
[14] Engan K, Skretting K, and Hussy J H. Family of iterative LS-based dictionary learning algorithms, ILS-DLA, for sparse signal representation[J]., 2007, 17(1): 32-49.
[15] Djurovi I, Simeunovi M, Djukanovi S,.. A hybrid CPF-HAF estimation of polynomial-phase signals: detailed statistical analysis[J]., 2012, 60(10): 5010-5023.
欧国建: 男,1975年生,博士生,研究方向为压缩感知、扩频通信、非平稳信号处理.
杨士中: 男,1937年生,教授,中国工程院院士,研究方向为信息与通信工程、电子科学与技术.
蒋清平: 男,1976年生,博士,讲师,研究方向为压缩感知、循环谱信号处理.
A Dictionary Learning Algorithm for Denoising Cubic Phase Signal
Ou Guo-jian①②Yang Shi-zhong①Jiang Qing-ping①Cao Hai-lin①
①(&,,400044,)②(,401331,)
Cubic Phase Signal (CPS); Recursive Least Squares Dictionary Learning Algorithm (RLS-DLA); Dictionary learning; Non-Linear Least Squares (NLLS); Curve fitting
TN911.7
A
1009-5896(2014)02-0255-05
10.3724/SP.J.1146.2013.00726
欧国建 ouguojia_2005@qq.com
2013-05-23收到,2013-10-25改回
国家自然科学基金(51377179),中央高校基本科研业务费(CDJZR12160020)和重庆教委项目(KJ120510)资助课题

