谐波阻抗和背景谐波电压 估算方法的对比研究
张 龙 陈西平 李洪杰 刘 斌 孙振权
(1.西安交通大学电气工程学院,西安 710049;2.陕西省地方电力集团,西安 710061)
电能既是一种经济、实用、清洁且容易控制的能源形态,又是电力部门向电力用户提供由发、供、用三方共同保证质量的特殊商品,因此,它同其他商品一样要讲求质量[1]。围绕电能质量的含义,从不同角度理解一般包括电压质量、电流质量、供电质量和用电质量[2]。在复杂配电系统中,除了个别大型谐波源负荷能确定其位置,系统中还有许多由不同类型和容量的用电设备按照一定网络结构组成的综合谐波负荷。在实际应用中检测点将受到一定限制,因此通过对公共连接点的测量,寻找出准确、实用的对配电系统谐波源定位和检测与用户谐波发射水平的测量方法,制定一套反映系统和用户对公共连接点谐波污染责任的指标是当务之急[3-6]。
国内外对谐波发射水平的估计方法主要是围绕对系统侧和用户侧谐波阻抗的估算来展开。现有的谐波阻抗估计方法基本可以分为“干预式”和“非干预式”两大类[7-8]。“干预式”方法主要包括注入法、开关元件法等,通过向系统强迫注入谐波电流或者间谐波电流,或是开断系统某一支路来测量谐波阻抗。该类方法会对系统运行造成不利影响,因此不能广泛使用。“非干预式”方法主要包括波动量法、线性回归法等,利用系统自身的谐波源和可测量参数等来估计谐波阻抗和谐波电压[9-12]。
本文研究分析了基于独立随机矢量协方差特性和基于二元线性回归这两种谐波发射水平评估方法的基本原理,利用PSCAD 仿真软件建立三电压等级、整流负荷仿真模型,通过Matlab 计算谐波阻抗和背景谐波电压,进而估算出用户谐波发射水平。最后,在IEEE 14 节点系统模型中改变负荷类型等条件,对比两种方法计算谐波阻抗和背景谐波电压的能力。
1 基本原理
h次谐波等值电路如图1所示。
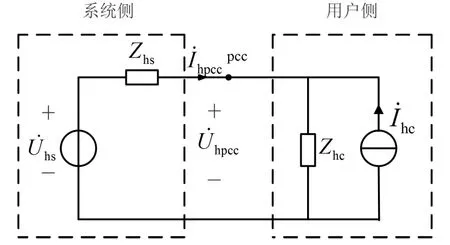
图1 系统侧与用户侧某次谐波等值电路
1.1 基于独立随机矢量协方差特性的评估方法
基于独立随机矢量协方差特性的谐波发射水平评估方法根据公共连接点处谐波电流与系统背景谐波只有弱的联系,利用随机矢量协方差特性抵消偏差量方程中背景谐波变动项,解得系统侧谐波阻抗,并跟踪计算用户谐波电压发射水平[13]。
根据等值电路列方程
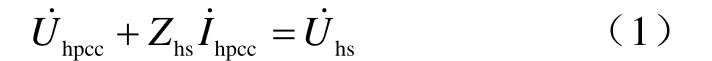
实际系统中,估计时段内(N个样本点)系统侧谐波阻抗基本不变,对式(1)求均值得
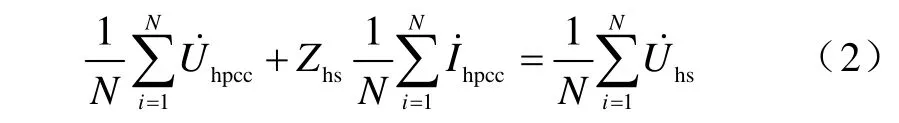
式(1)减式(2)得
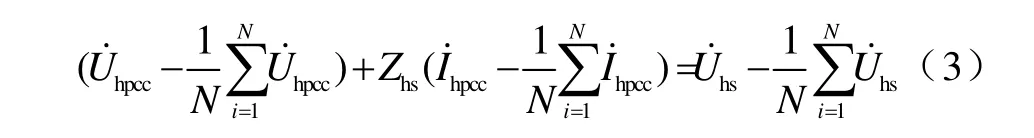
由图1知

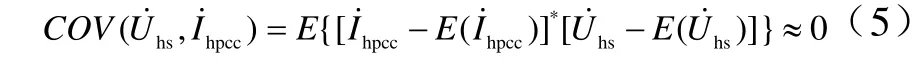
式中,*表示对复数求共轭。
实际计算中,若样本点足够多,期望可近似体现为均值,因此式(5)近似为
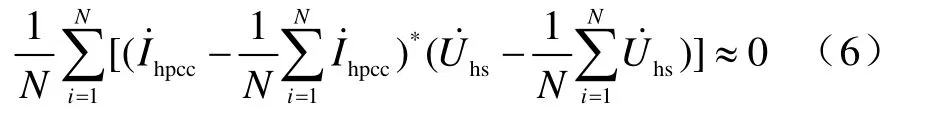
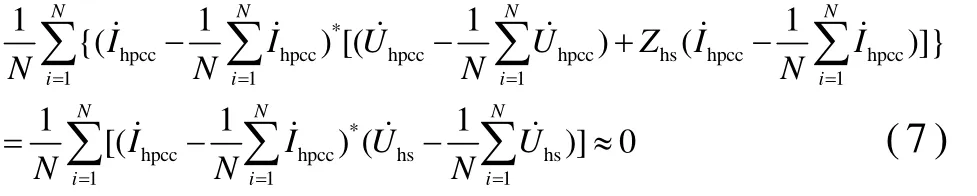
则式(7)变形为
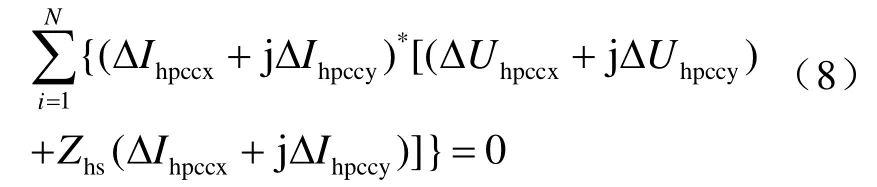
解得系统谐波阻抗实部和虚部分别为
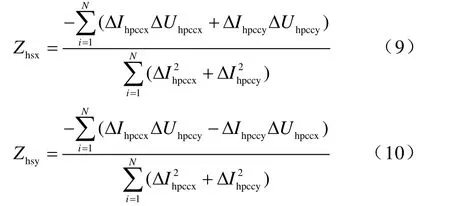
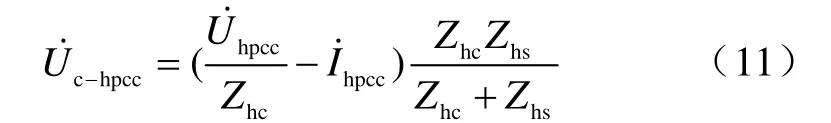

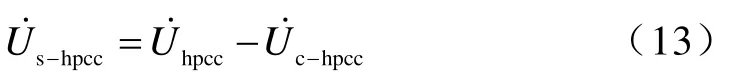
1.2 基于二元线性回归的评估方法
基于二元线性回归的用户谐波发射水平估计方法是在假定系统侧基本稳定的条件下,以公共连接点谐波电压、电流测量参数为观测数据,根据系统和用户等值电路推导的二元回归方程求取系统侧谐波阻抗,进而计算用户谐波发射水平[14]。
根据等值电路列方程
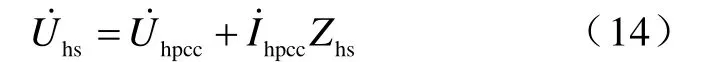
按实部、虚部分开有
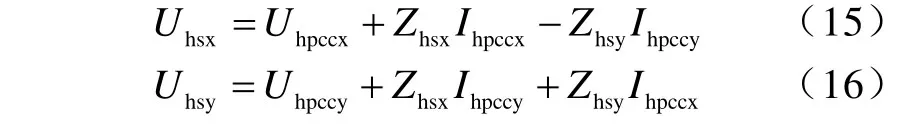
式中,*x为实部,*y为虚部。
由式(16)变换可得
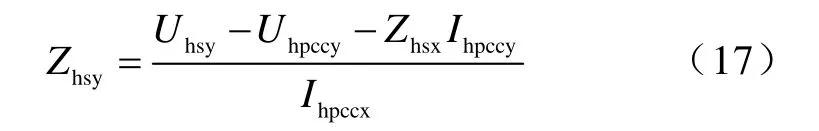
或
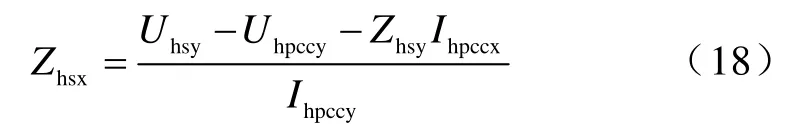
将式(17)代入式(15)整理得
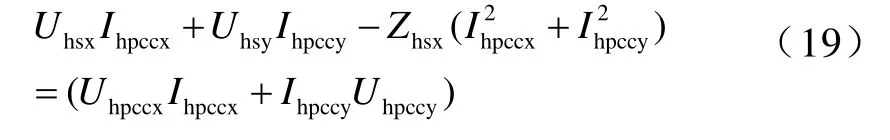
将式(18)代入式(16)整理得
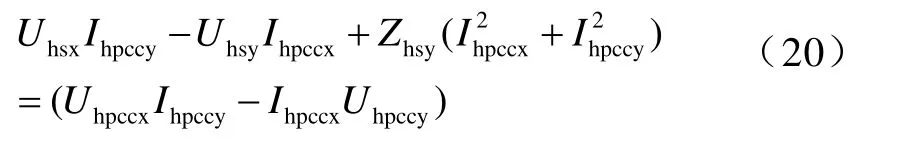
式(19)、式(20)中未知变量分别为Uhsx、Uhsy、Zhsx和Uhsx、Uhsy、Zhsy,根据二元线性回归分析方法可以由测量值求取它们的估计值。其中,两对Uhsx和Uhsy作为系统谐波电压源最小方差估计值,而Zhs=Zhsx+ jZhsy为系统侧谐波阻抗。
由图1和式(14)得
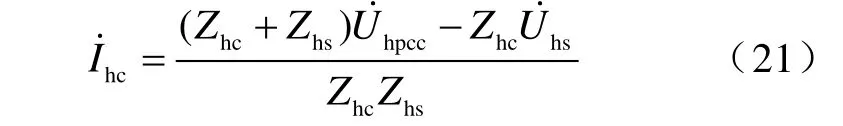
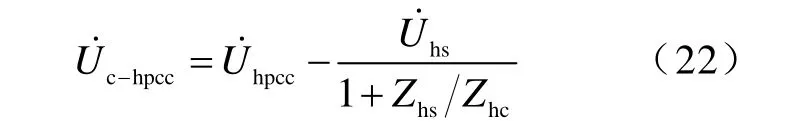
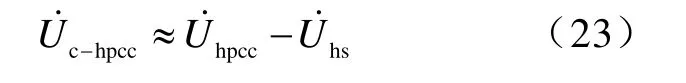
2 仿真分析
2.1 原理模型仿真计算
用PSCAD 根据系统侧与用户侧某次谐波等值电路搭建原理仿真模型如图2所示。
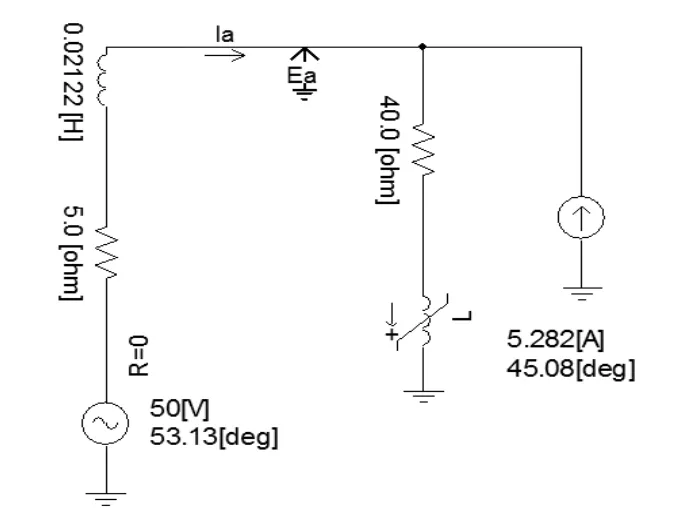
图2 原理仿真模型
系统频率为50Hz,元件参数如图2中所示。系统侧等值三次谐波阻抗为5.0+j20.0(Ω);用户侧等值三次谐波阻抗为40.0+j296.0(Ω)。该模型用随机函数发生器产生在-0.002~0.002 之间随机变化的数值控制用户侧电抗,模拟系统产生波动,发出谐波。PCC电压Ea和电流Ia经FFT 处理。设定采样频率为4000Hz,测量时间为10 个周波,测量间隔为0.8s。
在PCC 抽样三次谐波电压、电流80000 个点的波形数据如图3所示。分段(20 段,每段4000 个点,测量每段前800 个点,测量间隔为3200 个点)计算所得系统侧谐波阻抗如图4所示。
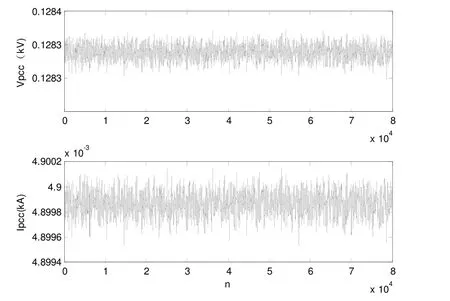
图3 PCC 三次谐波电压幅值和电流幅值的采样数据
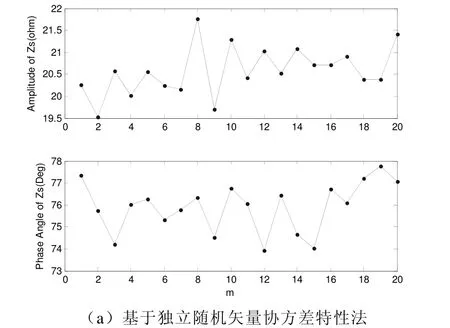
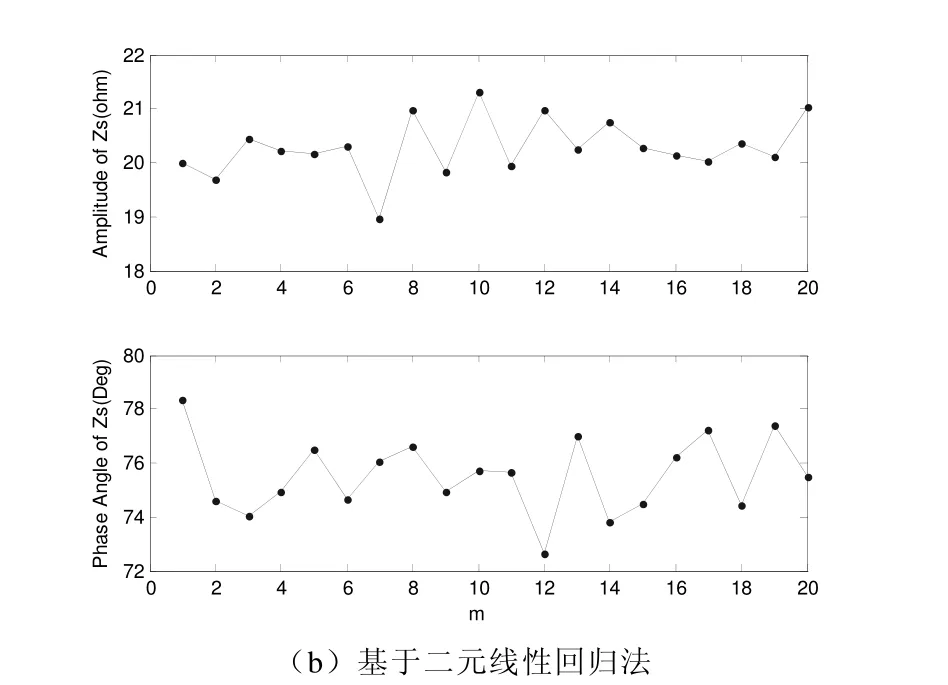
图4 系统侧谐波阻抗
总共16000 个测量点的PCC 电压幅值Vpcc和按照谐波阻抗重新计算的系统侧谐波电压幅值Vs-pcc如图5所示。用户谐波电流在PCC 引起的电压降幅值Vc-pcc如图6所示。
两种方法的计算结果如表1所示,与设定值十分接近,误差较小,这说明两种方法在计算系统谐波阻抗和背景谐波电压中具有可行性、准确性。
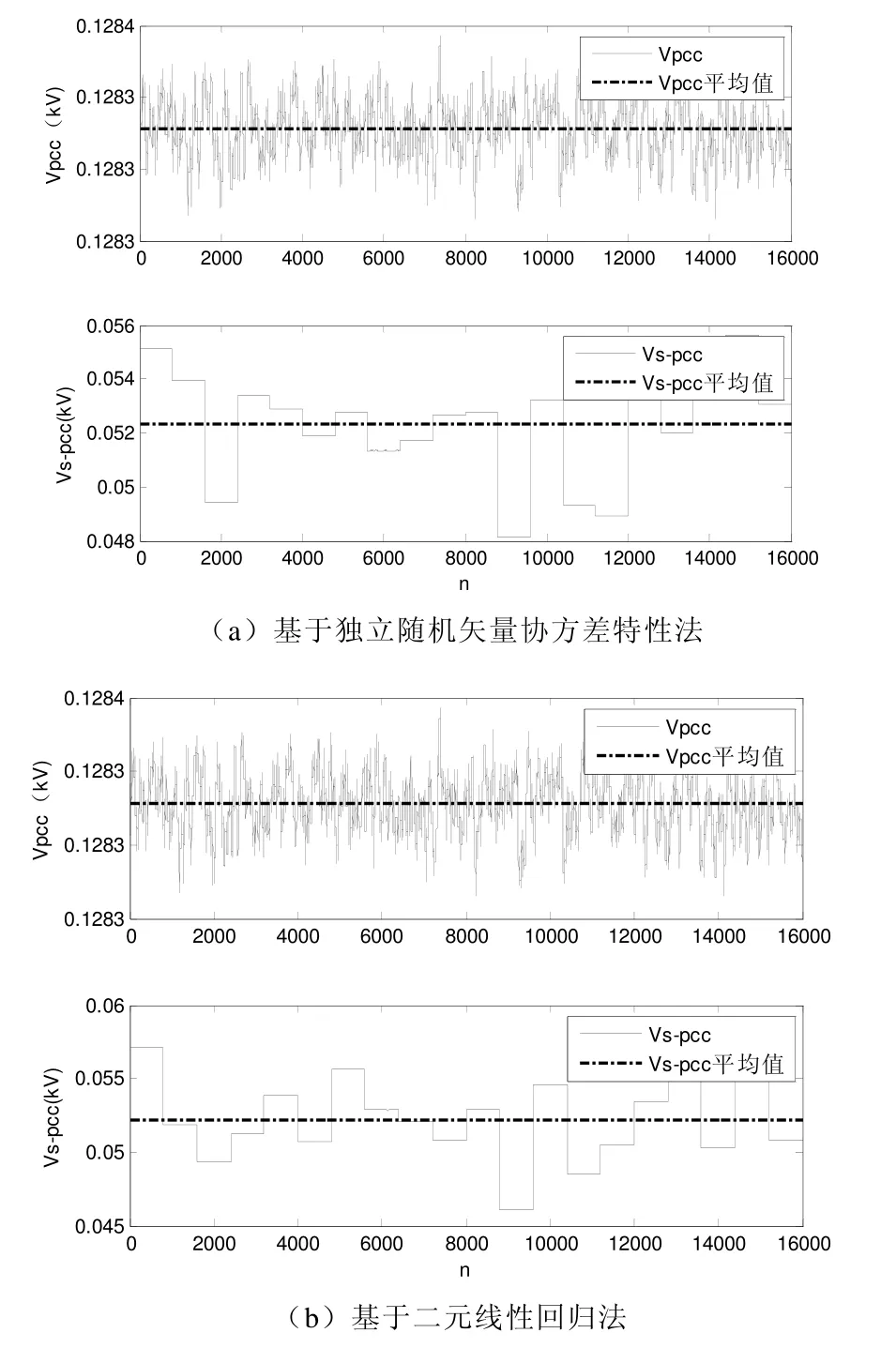
图5 PCC 和系统侧谐波电压在16000 个测量点的计算值
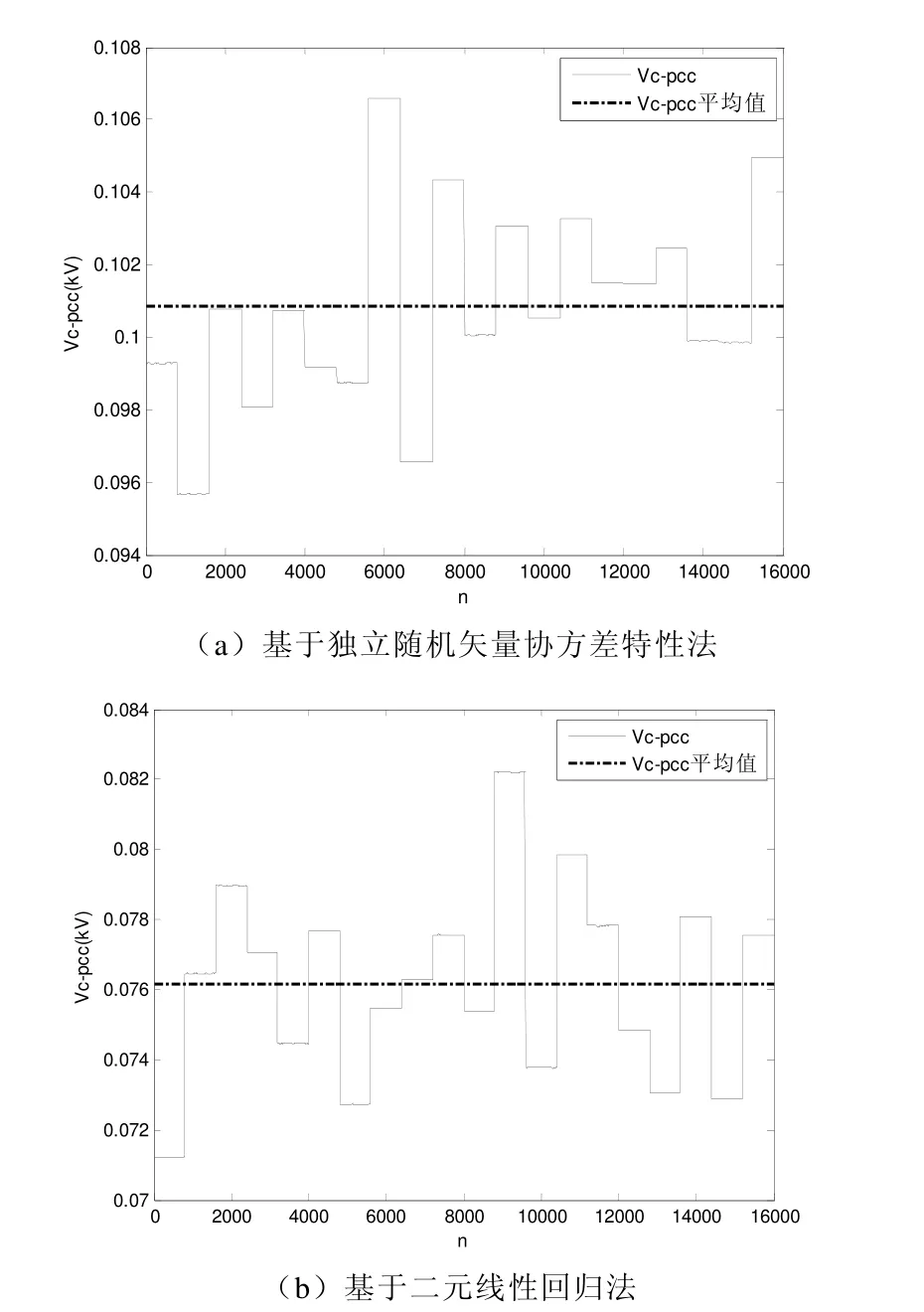
图6 用户侧谐波电流在PCC 引起的电压降 Vc-pcc
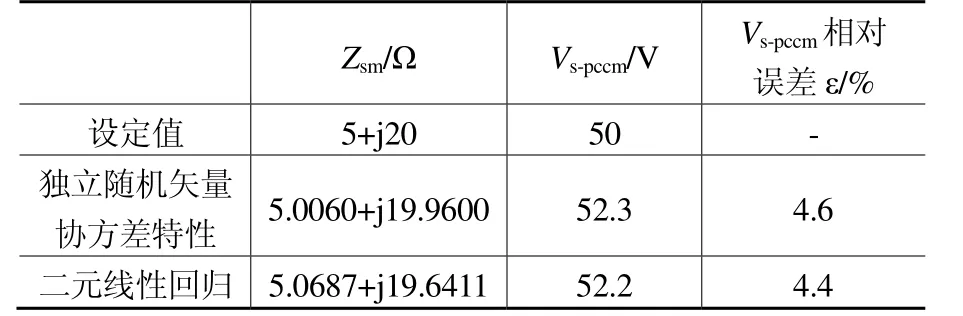
表1 原理模型中三次谐波计算分析结果比较
2.2 三电压等级模型仿真分析
参照某实际变电站接线,利用PSCAD 搭建三电压等级、整流负荷模型简化电路如图7所示。
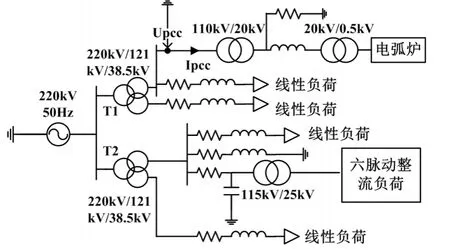
图7 三电压等级、整流负荷仿真模型简化电路图
该模型包括 220kV、110kV 和 35kV 三个电压等级,相关参数如图7所示。变压器T1 110kV 母线作为PCC,采集其电压和电流,用户侧连接的负荷包括电弧炉。电弧炉在炼钢过程中表现出的强烈随机性和时变性,会引发电力系统诸多电能质量问题,它产生的谐波对电网影响最大[15]。变压器T2 110kV母线上连接6 脉动整流负荷。其它负荷均为线性负荷,有功功率为10MW,无功功率为8Mvar。
数据采样、处理方法同1.1。图7模型中将系统侧电源置零,用户侧电弧炉断开,在用户侧连接一个三次谐波电压源,测量PCC 三次谐波电压和三次谐波电流,用谐波电压除以谐波电流,计算出系统侧三次谐波阻抗的实际值Zs= 0.1560 + j12.5040。
两种方法计算系统谐波阻抗Zsm、背景谐波电压Vs-pccm、用户谐波发射水平Vc-pccm、用户谐波发射水平占PCC 该次谐波电压的比例Vc-pccmVpccm如表2所示。
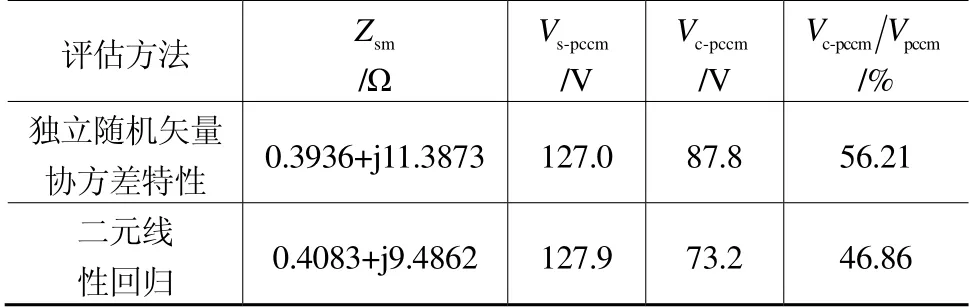
表2 三电压等级模型中三次谐波计算结果比较
由表2看出两种方法计算系统谐波阻抗、背景谐波电压和用户谐波发射水平的结果比较相近。“基于独立随机矢量协方差特性法”计算出系统谐波阻抗的幅值变化范围为9.8~12.9Ω,“基于二元线性回归法”为6.6~12.1Ω。相比之下,第一种方法计算出的谐波阻抗变化范围较小。将计算出的系统谐波阻抗与实际的谐波阻抗Zs比较,发现第一种方法的计算值与实际值更为接近。
在三电压等级模型中,谐波源除了电弧炉外还有一个六脉动整流负荷,六脉动整流负荷产生的谐波对于PCC 来说属于系统侧,因此用户侧谐波源的谐波发射水平占PCC 该次谐波电压的比例较低。
2.3 IEEE 14 节点模型分析
在PSCAD 中对图8所示的IEEE14 节点标准测试系统进行仿真计算。
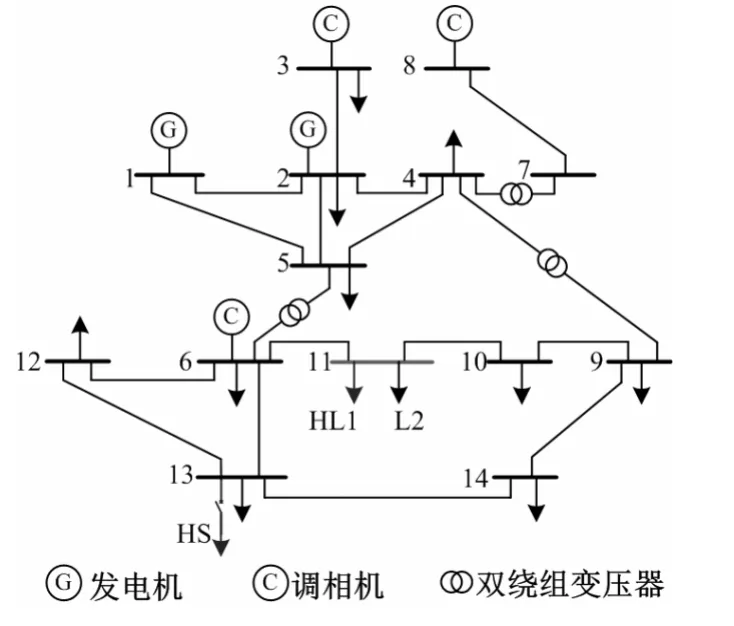
图8 IEEE14 节点系统模型
该系统由两台发电机组、3 台同步调相机、14条母线、15 条输电线路和3 台变压器组成。计算中,将发电机和同步调相机等值为次暂态电抗,变压器等值为阻抗,输电线路以π 型等值电路表示[16],同时考虑长距离输电线对地电容。
设定母线11 为PCC,HL1、L2 为母线处接入的两个负荷,其中HL1 为负荷侧谐波源;L2 为线性负荷。同时母线13 处接入谐波源负荷HS。将除去负荷 HL1、L2 的网络其余部分视为该模型的系统侧,仿真计算HL1 谐波源负荷在母线11 处产生的定量谐波责任。
1)单谐波源的IEEE 14 节点模型分析
断开母线13 处的谐波源负荷HS,使整个系统仅含用户侧谐波源HL1。在单谐波源IEEE 14 节点模型中将系统侧电源置零,用户侧谐波源HL1 断开,在用户侧连接一个三次谐波电压源,测量母线11 的三次谐波电压和三次谐波电流。计算出系统侧三次谐波阻抗实际值Zs= 0.0473 + j0.4082。
2)两个谐波源的IEEE 14 节点模型分析
接入母线13 处的谐波源负荷HS,使系统侧和用户侧均含谐波源,从而改变系统谐波。在两个谐波源IEEE 14 节点仿真模型中将系统侧电源置零,用户侧谐波源HL1 断开,在用户侧连接一个三次谐波电压源,测量公共连接点的三次谐波电压和三次谐波电流。计算出系统侧三次谐波阻抗的实际值Zs= 0.0486 + j0.4078。
两种方法计算出单谐波源和两个谐波源情况下系统谐波阻抗Zsm、背景谐波电压Vs-pccm、用户谐波发射水平Vc-pccm、用户谐波发射水平占PCC 该次谐波电压的比例Vc-pccmVpccm如表3所示。

表3 IEEE 14 节点模型中三次谐波计算结果
从单谐波源IEEE 14 节点仿真结果看出“基于独立随机矢量协方差特性法”计算出系统谐波阻抗的幅值变化范围为0.387~0.402Ω,“基于二元线性回归法”为0.376~0.393Ω。相比之下,第一种方法计算出的谐波阻抗变化范围较小,而且与实际系统谐波阻抗Zs更为接近。
从两个波源的IEEE 14 节点仿真结果看出“基于独立随机矢量协方差特性法”计算出系统谐波阻抗的幅值变化范围为0.386~0.397Ω,“基于二元线性回归法”为0.369~0.389Ω。相比之下,还是第一种方法计算出的谐波阻抗变化范围较小,并且与实际系统谐波阻抗Zs更为接近。
在IEEE 14 节点模型中,通过将系统侧加入谐波源而其他结构不变来改变系统侧谐波参数,对比两种方法在系统侧加入谐波源前后的各计算量,得出系统侧谐波变化对整个网络的影响情况。通过结果分析发现,两种方法计算出的系统侧谐波阻抗均要降低;系统侧谐波电压升高;用户侧谐波电压基本保持不变;用户谐波发射水平占PCC 谐波电压的比例均比系统侧未加入电弧炉的仿真结果低。
在系统模型中,若能进一步探究出如何逐项依次改变谐波相角、系统谐波阻抗以及谐波电压的变化对估算结果的影响,必将可以更加细致地对两种方法估算谐波发射水平的能力进行比较。
3 结论
本文通过大量仿真实验对“基于独立随机矢量协方差特性”和“基于二元线性回归”两种谐波发射水平评估方法进行了对比研究,得出以下结论:
1)两种方法在估算用户谐波发射水平的计算中都具有很高的准确性,得出的结果具有一致性。
2)两种方法的计算结果比较相近,但用独立随机矢量协方差特性的方法比用二元线性回归法计算出的系统谐波阻抗幅值的波动范围要小,稳定性较好,而且与实际值更为接近,而基于二元线性回归法计算出的背景谐波电压与实际设定值的相对误差更小。
3)系统侧增加谐波源后系统侧谐波阻抗降低,系统侧谐波电压要增大,用户侧谐波电压基本保持不变,用户谐波发射水平占PCC 处谐波电压的百分比降低。
[1] 肖湘宁,徐永海.电能质量问题剖析[J].电网技术,2000,24(3):36-38.
[2] Bollen M H J.Understanding power quality problems.Voltage sags and interruption[M].New York:IEEE PRESS,2000.
[3] 王安,粟时平,邓奇峰,等.基于小波变换的暂态电能质量扰动检测与定位研究[J].电气技术,2012(4):21-25.
[4] 胡铭,等电能质量及其分析方法综述[J].电网技术,2000,24(3):36-38.
[5] Wilsun Xu,YiLu Lin.A method for determining customer and utility harmonic contribution at the Point of common coupling[J].IEEE Transactions on Power Delivery,2000(15):804-811.
[6] 贾秀芳,华回春,曹东升,等.基于复线性最小二乘法的谐波责任定量划分[J].中国电机工程学报,2013(4): 149-155,20.
[7] Yang H,Porotte P,Robert A.Assessing the harmonic emission level from one particular customer.Proceedings of PQA`94[A].Amsterdam: EPRI of USA[C].1994: B-2.08.
[8] Srinivasan.K.On separating customer and supply side harmonic contributions[J].IEEE Transactions on Power Delivery,1996,112(4): 1003-1012.
[9] 张安安,杨洪耕.基于畸变波形同步分层估计谐波阻抗的探讨[J].电力系统自动化,2003(9):41-44.
[10] 赵勇,张涛,李建华,等.一种新的谐波源简化模型[J].中国电机工程学报,2002(4):47-52.
[11] Wilsun Xu,Yilu Liu.A method for determining customer and utility harmonic contribution at the point of common coupling[J].IEEE Transactions on Power Delivery,2000,15(2):3-16.
[12] 赵勇,沈红,李建华,等.谐波源的识别及其与非谐波源的分离方法[J].中国电机工程学报,2002(5):85-88.
[13] 惠锦,杨洪耕,林顺富,等.基于独立随机矢量协方差特性的谐波发射水平评估方法[J].电力系统自动化,2009(7): 27-31.
[14] 张巍,杨洪耕.基于二元线性回归的谐波发射水平估计方法[J].中国电机工程学报,2004(6):54-57.
[15] 张峰,何新,杨丽君.用于电能质量分析的电弧炉仿真模型[J].电气技术,2013(7):34-38.
[16] Gursoy E,Niebur D.Harmonic load identification using complex independent component analysis[J].IEEE Transactions on Power Delivery,2009,24(1):285-292.

