基于磁控电抗器的变电站无功补偿策略

周强强 杨 波 陈杰明 王 晨

（1.广州供电局，广州 510640；2.华中科技大学电气与电子工程学院，武汉 430074）

随着现代电力系统规模的不断发展，对于无功补偿的要求也不断提高，不仅需要提供容性无功来保证负荷高峰期时系统电压的稳定，而且还需要提供感性无功来平衡电缆的充电功率防止系统电压过高。磁控电抗器能够实现感性无功的可控调节，与分级电容器组组成的动态无功补偿装置能够实现感性容性较为连续的无功调节，并具有成本低、占地面积小、维护简便等特点，满足现代电力系统的要求，具有广阔的应用前景[1-3]。

工程应用中由感性无功补偿设备、容性无功补偿设备组成的动态无功补偿装置能够实现感性容性的无功连续可调，主要采用无功补偿分区策略进行控制，并通过PΙ 闭环的控制方式实现。静止无功补偿器（SVC）、静止同步补偿器（STATCOM）等动态无功补偿装置均广泛采用无功补偿分区的控制策略，但应用于配电网中的磁控电抗器的无功补偿控制策略方面的研究仍有待进一步探索。

本文借鉴无功补偿分区控制的思想，提出了一种基于变压器低压侧电压的多模式电压与无功补偿的最优控制策略，并通过瞬时无功功率理论的双闭环PΙ 控制系统实现。该策略不仅能够在系统电压异常时采取紧急的无功补偿控制以抑制系统电压突变，同时能够在系统电压正常时实现变压器有功损耗最少的无功补偿控制。

1 控制策略的基本思想

本文提出的电压与无功补偿的最优控制策略由控制电压判断、无功控制模式选择、无功补偿控制系统及MCR、FC 开关控制、MCR 与FC 组成的动态无功补偿装置四个部分组成，其流程图如图1所示。

图1 电压与无功补偿最优控制策略流程图

该策略将变电站的站内变压器低压侧电压作为控制电压，将MCR、FC 组成的动态无功补偿装置作为控制对象，同时将变电站作为控制单元。考虑到变电站中不同工况下对于无功补偿控制策略实时性的要求的差异，根据控制电压的情况将无功补偿的控制模式分为无功优化控制模式、低电压紧急控制模式、高电压紧急控制模式三种控制模式。电压与无功功率的最优控制策略的过程如下。

1）在每个控制周期内以经过傅里叶变换的变电站的站内变压器低压侧电压基波的有效值作为控制电压进行判断。

2）根据1）中的判断结果选择相应的无功补偿模式。当控制电压在规定范围内时，选择无功优化控制模式；当控制电压低于下限门槛值时，选择低电压紧急控制模式；当控制电压高于上限门槛值时，选择高电压紧急控制模式，本文低电压、高电压的门槛值分别取为0.85、1.15。

3）根据2）中所选择的控制模式，输出相应的目标无功补偿功率，MCR、FC 各自的开关控制信号至无功补偿控制系统；

4）按照3）输出的目标无功补偿功率，利用基于瞬时无功功率理论的双闭环PΙ 控制系统，输出MCR 晶闸管的触发信号；按照3）中输出的MCR、FC 各自的开关控制信号，分别控制MCR 的连接开关与FC 的投切开关。为了防止控制时暂态过程造成开关的频繁动作影响开关的寿命，本文采用了短时闭锁的措施，即MCR、FC 开关状态一旦改变就闭锁开关状态一段时间后才开放。

5）继续上述步骤1）至4）不断对控制电压进行判断，执行相应的措施。

2 无功补偿的控制模式

2.1 无功优化控制模式

无功优化控制模式针对的是变电站正常运行阶段。变电站正常运行时，无功补偿的作用对于电力系统而言是提高功率因数，减少线路与设备的有功损耗；对于用户而言是保持电压稳定，保障工作与生活。在变电站中最主要的有功损耗来源是站内变压器，因此，变电站无功优化控制应以站内变压器有功损耗作为目标函数，同时以电压、无功补偿容量、功率因数作为约束条件，从而得到最优的目标无功补偿功率。变电站无功优化的目标函数与约束条件如式（1）、（2）所示。

目标函数：

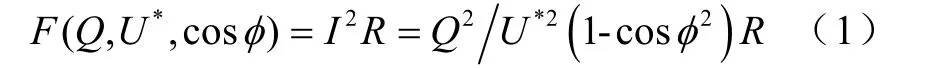
式中，F表示站内变压器的有功损耗；Q、U*、cosφ表示站内变压器低压侧出口处的无功功率、电压、功率因数；R表示站内变压器的等效电阻；QH、QL表示无功功率的上、下限，UH*、UL*表示电压的上、下限， cosφH、cosφL表示功率因数的上、下限。

此优化问题是在满足约束条件的前提下，实现目标函数的最小化，属于二次规划问题，本文选择采用遗传算法与基于内点反射牛顿非线性规划算法相结合进行问题求解。遗传算法具有很强的全局搜索能力，基于内点反射牛顿算法则具有很强的局部搜索能力，两种方法相结合能够快速地搜索出问题的最优解。

优化问题的解决算法步骤如下：

1）遗传算法、非线性规划算法的参数初始化。即根据变电站站内变压器的无功优化问题的规模确定遗传算法的种群规模与进化代数；根据式（2）中目标函数的Q、U*、cosφ三个变量确定遗传算法的染色体数；根据式（2）中约束条件的确定遗传算法的染色体约束，同时根据目标函数与约束条件确定非线性规划算法的目标函数与约束条件。

2）根据公式（2）的目标函数构建遗传算法的适应度函数，并计算出种群的初始值。

3）对遗传算法种群中各代的个体分别进行选择、交叉、变异，将较优的个体遗传到子代，同时在种群每10 代进化中得到一个全局搜索的最优解Q0、U*0、cosφ0。

4）采用非线性规划算法以步骤3）中的全局最优解Q0、U*0、c osφ0为初始值进行局部搜索，得到局部搜索的最优解。

5）判断遗传算法中种群的进化代数直至满足步骤1）设定的进化代数则终止计算，并输出最后一组局部搜索的最优解Q1、U*1、cosφ1作为问题的最优解Qop、U*op、cosφop。

2.2 低电压紧急控制模式

低电压紧急控制模式针对的是变电站低压侧电压过低的运行工况。此处的电压过低主要指系统发生故障造成电压大幅度降低，可能对系统的稳定以及用户的设备造成较大影响的情况。

由于容性无功补偿能够提高电压水平，因此应将变电站内FC 的全部容量投入，同时将产生感性无功的MCR 退出运行。该模式直接输出MCR、FC 的开关控制信号，从而提高无功补偿控制的响应速度。

2.3 高电压紧急控制模式

高电压紧急控制模式针对的是变电站低压侧电压过高的运行工况。此处的电压过高主要指系统负荷突然大量减少或者投入大容量的容性负荷造成电压大幅度升高，造成系统有功损耗的大量增加以及用户设备的损坏。由于感性无功补偿能够抑制电压升高，因此应将变电站内的FC 全部退出运行，同时将MCR 的容量全部投入，考虑到具体工况的差异MCR 的投入容量也可根据实际情况整定。该模式同样采用直接输出开关控制信号，以提高无功补偿控制的响应速度。

3 无功补偿的控制系统

根据控制电压的情况，选择无功补偿控制模式，输出目标无功补偿功率，通过采用无功补偿的控制系统采集变电站的实际工况，对动态无功补偿装置中MCR 的晶闸管触发进行有效控制，实现MCR 无功补偿功率的准确跟踪。

3.1 基于瞬时无功功率理论的检测法

瞬时无功功率理论的基本思路是通过坐标变换将三相系统电压电流变换为两相正交电压电流矢量，并定义了三相系统的瞬时有功功率和瞬时无功功率[4-5]。

瞬时无功功率理论的检测方法分为p-q 检测法与ip-iq检测法两种，其中ip-iq检测法仅采集电压信号的相位，同时只对电流信号进行变换，避免了电压信号造成的畸变的影响，简化了变换的过程，本文选择采用此检测法。

ip-iq检测法先将 三相电流ia、ib、ic变换为αβ坐标系的两相电流iα、iβ，再将有功分量与无功分量进行分解，得到电流的有功分量ip和无功分量iq。ip-iq检测法变换过程如图2所示。

图2 ip - iq检测法原理图

3.2 双闭环PI 控制系统

控制系统采用双闭环PΙ 控制实现，控制系统的流程图如图3所示。

图3 双闭环PI 控制系统流程图

控制系统外环为无功功率环，将所选择的控制模式输出的目标无功补偿功率Qf与站内变压器低压侧无功功率Q进行比较经PΙ 调节后，得到目标ip、iq经pq/abc 变换为目标iaf、ibf、icf输出到内环。内环为电流环，将内环输出的目标iaf、ibf、icf与站内变压器低压侧出口处测得的三相电流ia、ib、ic进行比较后通过傅里叶变换得到目标基波有效值经PΙ 调节后，得到MCR 触发系统的触发信号αa、αb、αc。

4 算例分析

以广州某110kV 变电站为例进行算例分析。该变电站电压采取标幺值，1pu=10kV；负荷为3MW+j1.8054Mvar；FC 分为两级，每级容量均为-j2Mvar，共-j4Mvar；MCR 容量为j2Mvar。变电站拓扑图如图4所示。

图4 变电站拓扑图

4.1 磁控电抗器的仿真建模

通过分析磁控电抗器的结构与工作原理，文献[6]提出了磁控电抗器的等效物理模型和数学模型，文献[7]在此基础上，提出了等效电路模型，该模型既能反映数学模型的物理规律，同时简捷有效满足仿真分析的要求。本文选择按照该模型建立磁控电抗器的仿真模型，磁控电抗器的等效模型如图5所示。

4.2 控制策略的仿真分析

变电站的初始运行工况为：控制电压为1，功率因数为0.85，MCR、FC 均未投入。以MCR、FC 均投入后的运行工况为例，分析控制策略的无功补偿效果。

图5 磁控电抗器等效模型

1）改变变电站接入系统处的电压大小，仿真系统发生电压波动的工况。为了节省篇幅，本文将电压波动的各事件集中于同一时间轴，利用所提出的控制策略进行无功补偿控制，并与无控制策略的情况进行对比分析。假设0～2s 时系统电压处于正常水平，2～3.5s时电压降低为0.8；5～6.5s 时系统电压升高为1.2；3.5～5s、6.5～8s 时系统电压均恢复为1。

2）仿真系统电压处于正常状态时所提出的控制策略的无功优化工况。将该策略与以功率因数为控制目标的控制策略进行对比分析。

仿真结果如图6、图7所示，图6为电压波动的仿真结果；图7为无功优化对比的仿真结果。

图6 电压波动的仿真结果

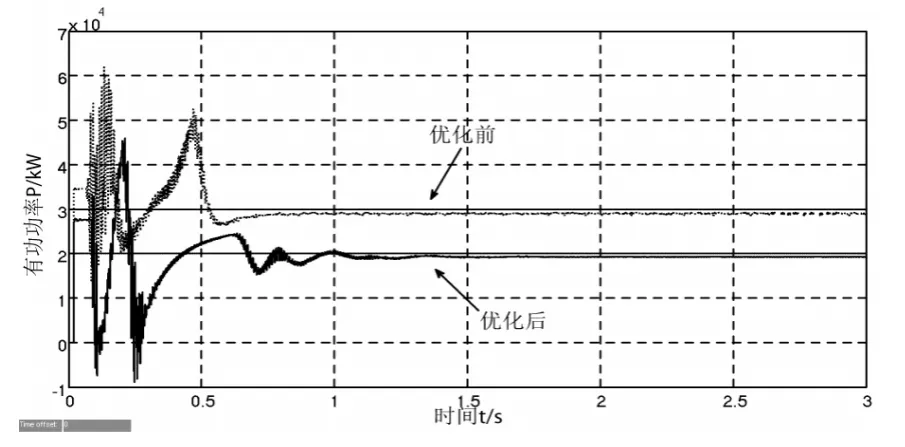
图7 无功优化对比的仿真结果

分析上述仿真结果可以得到以下结论：

1）由图6中可知，在系统电压波动时，没有采用该策略变电站电压随系统电压的波动而改变，超出变电站电压的正常运行范围。而采用该策略能够保证变电站电压的稳定。2～3.5s、5～6.5s 期间，系统电压发生上下波动后变电站电压均能稳定在正常范围内，从而抑制电压发生突变；0～2s、3.5～5s、6.5～8s 期间，系统电压处于波动后的恢复阶段也具有同样的特点。

2）由图6中可知，该策略在控制电压建立阶段对MCR、FC 的开关信号实施0.5s 闭锁，以及在系统电压发生波动时，对开关信号实施闭锁的措施，能够有效地避免暂态过程的影响，防止MCR、FC开关出现频繁投切的现象，影响开关寿命，同时还有利于变电站电压快速保持稳定。

3）由图7中可知，在系统电压正常运行时经过约0.5s 的无功补偿的优化暂态过程后，变电站站内变压器的有功损耗将达到稳定值，该策略相比于以功率因数为控制目标的控制策略而言，有功损耗明显较低，能够有效地将站内变压器的有功损耗优化至最低水平。

5 结论

本文提出了一种电压与无功补偿的最优控制策略，以变压器低压侧电压作为控制电压进行判断，将无功补偿控制模式划分为三种类型，并采用基于瞬时无功功率理论的双闭环PΙ 控制系统来实现。通过对配备MCR、FC 组成的动态补偿装置的变电站进行仿真分析，结果表明该策略在系统电压发生波动时能实现无功补偿的正确有效控制；同时在系统电压正常时能实现变电站有功损耗最小的无功优化。

[1] 陈柏超.新型可控饱和电抗器理论及应用[M].武汉:武汉水利电力大学出版社,1999.

[2] 张建兴,王轩,雷晰,等.可控电抗器综述[J].电网技术,2006(30): 269-272.

[3] 欧阳永坚,周雄健.基于磁控电抗器的新型动态无功补偿装置应用效益分析[J].电网技术,2006,29(30): 210-213.

[4] 唐蕾,陈维荣.瞬时无功功率理论坐标变换的推导及谐波电流检测原理分析[J].电网技术,2008,32(5):66-69,89.

[5] 王兆安,李民,卓放.三相电路瞬时无功功率理论的研究[J].电工技术学报,1992(3):39,55-59.

[6] 田铭兴,励庆孚,王曙鸿.磁饱和式可控电抗器的等效物理模型及其数学模型[J].电工技术学报,2002,17(4):18-21,35.

[7] 田铭兴,励庆孚,王曙鸿.磁饱和式可控电抗器的等效电路及仿真分析[J].电工技术学报,2003,18(6):64-67.