基于粗糙集的航空灾害协同预警研究

张 洋，刘勇军，刘 伦

(武汉理工大学 管理学院，湖北 武汉430070)

一切危害民航正常航空运营活动、运营秩序以及社会政治经济生活的事故或事件所造成的灾难性后果，称之为航空灾害，同时兼具生成突发性、成因综合性和一定可防性等特征。国际民航组织曾对世界航空飞行事故进行统计得出：飞行事故中由单一因素造成的占比28%，双因素占比54%，多因素占比18%。笔者仅针对多因素造成的航空灾害诸多事件采用粗糙集方法对其进行协同预警研究。换言之，笔者主要采用粗糙集理论方法对航空灾害协同预警指标体系中诸多指标以及预警级别进行运算分析及规则提取，获得科学准确的预警信息。

在航空灾害协同预警过程中，主要存在3 个问题：①从大量已有完全灾害数据信息中挖掘出预警规则;②从实时不完全灾害数据信息中找出规则;③判定所获取预警规则的有效性和合理性。粗糙集理论方法的应用可以较好地解决前两个问题，因为它是一种能够处理不精确、不相容和不完全数据的新型数学工具，而对于第3 个问题，笔者引入了概率粗糙集的方法来提取更为有效和合理的预警规则。

总而言之，为了更好地解决航空灾害协同预警中存在的3 个问题，笔者考虑航空灾害协同预警数据信息中存在的“不相容”和“有序”特性，建立基于绝对有序多属性概率粗糙集的航空灾害协同预警研究模型和方法，对其进行实例演算分析，以期实现从完全和不完全数据中提取出更为有效和合理的预警规则，规避类似的航空灾害事件，巩固民众对民航事业的信心。

航空灾害预警管理研究最早起源于20 世纪60 年代的国外危机和风险管理，针对的是国家关系和政治领域。而一直到20 世纪90 年代初，美国和欧洲才率先在航空领域利用预警思想，建立了多种预警系统。1989 年，美国联邦航空局安装风切变预警系统，法国应用里森的“因果理论”建立法航飞行安全组织开展事故预警。1995 年，美国FAA 提出要通过信息共享来实现预警功能。1997 年，FAA 系统安全办公室AOPA 提出投入一种新型的程序［1］，向AOPA 报告对机场产生威胁问题的预警;2000 年，HUNTER 博士应用航空事故风险指标对安全的预期性效果进行了研究［2］;FULLWOOD 应用线性叠加法对根据时间变化的安全趋势进行预测［3］;YOKOTA 提出了如何对机组进行培训和教育以实现有效的危机管理［4］。

我国关于协同预警研究的起步较晚，在20 世纪80 年代末、90 年代初，佘廉教授提出“企业逆境管理”的概念，之后于1993 年开始了企业预警管理系统的研究，在《企业逆境管理》中提到企业预警管理系统的设想并创立了企业预警管理体系。1995 年，中国南方航空公司建立了南方可靠性控制闭环系统，设立了数据可靠性标准［5］，并加强了可靠性分析。2004 年，罗帆等在《航空交通灾害预警管理》中对航空灾害预警管理系统的研究奠定了航空安全预警系统研究的理论指导地位。2008 年，《北疆牧区雪灾预警与风险评估方法》中提出了预警模型［6］。2010 年，《高速公路交通灾害预警模型研究》提出了未确知测度模型的应用［7］。但这些研究并未从定量的角度对航空灾害的成因进行深入分析，更缺乏对航空灾害预警机理和技术方法的研究。因此，笔者在此基础上利用基于粗糙集的方法对航空灾害的预警进行相关的研究。

1 模型构建

1.1 航空灾害协同预警指标体系

航空灾害的发生是人为失误或违规、飞机及相关设备失控或失灵、自然环境恶劣或突变、组织管理能力不足等4 种因素相互协同作用的结果。笔者构建的基于粗糙集的航空灾害协同预警指标体系如图1 所示。

系统地分析航空灾害中“人-机-环境-管理”四要素的相互协同作用和整体变化规律［8-9］。预警指标体系的构建因“不同要求，不同系统”而异，并不固定唯一，但不管系统如何构建指标体系，都需要能够切实反映出航空全过程所面临的实际状况［10］。

图1 基于粗糙集的航空灾害协同预警指标体系

1.2 航空灾害预警级别

航空灾害协同预警研究的目的是提取预警规则和提供日常监测，从而做出及时预警。在航空灾害协同预警中，航空灾害协同预警指标体系表示导致航空灾害发生的成因，航空灾害预警级别则表示航空运输过程中所将面临的危险程度，并设置预警危险程度和预警状态与之相对应。

笔者将航空危险程度定义为5 个层级：极高、高、中等、低和无灾害危险，并分别对应预警级别、信号和状态为：一级红色巨警、二级橙色重警、三级黄色中警、四级蓝色轻警、无色无警，在系统运行中分别对应不同级别和发出颜色预警信号如表1 所示。

表1 航空灾害预警级别表

1.3 基于粗糙集的航空灾害协同预警模型

将航空灾害协同预警指标体系中的每个预警指标视为一个条件属性，预警级别视为决策属性，构建基于粗糙集的航空灾害协同预警模型，如图2所示。该模型用矩形框表示要执行的处理信息或文档;菱形表示处理;在模型的左上方用虚线划出的是对已有的航空灾害数据进行粗糙集不完全数据处理及连续属性离散化处理，形成预警决策表。

通过粗糙集理论方法提取预警规则，再通过对航空过程中的灾害预警指标进行实时监测，对比预警规则，诊断出可能导致航空灾害的成因，有效预防灾害事故的发生。诊断的过程是对原有灾害数据的分析，总结归纳出规律及准则，然后对比实时监测数据，发出预警信号。

图2 基于粗糙集的航空灾害协同预警模型

1.4 基于粗糙集的航空灾害协同预警运行机制

基于粗糙集的航空灾害协同预警的基本构成主要包括：数据输入接口、数据库、模型库、方法库、知识库、预警模块，以及输出接口这几个部分［11］。其运行机制主要由两个部分组成。

(1)预警规则提取。首先通过人机交互将大量航空灾害原始数据输入后台数据仓库，然后抽取出协同预警指标体系和航空灾害预警级别传送至决策表模型库，再利用方法库中的粗糙集方法提取出决策规则［12］，产生基于原始数据的预警信息，为下一步的实时监控数据处理提供预警依据。

(2)实时预警决策。首先系统依据航空灾害预警指标体系中的各指标将航空运输全程环境监测数据自动通过输入接口传送至后台系统，对比上一步得到的决策规则，评判航空灾害预警级别，通过预警功能模块将预警信息输送到客户端。

基于粗糙集的航空灾害协同预警的运行机制如图3 所示。

图3 基于粗糙集的航空灾害协同预警运行机制

2 改进式绝对有序多属性概率粗糙集的航空灾害协同预警

2.1 有序多属性概率粗糙集的定义

基于有序多属性概率粗糙集的航空灾害协同预警核心主要有两点：①协同预警决策表中的属性值范畴是一种有序关系，即存在优劣、好坏、高低等排序关系，近似地建立一种优先权关系上的特殊有序二元关系，而非等价关系;②由于数据冗余的原因，通过使用粗糙集模型计算得出概率阈值，将确定性的等价关系划分为正域，不满足较低阈值的等价关系划分为负域，介于两者间的等价关系则划分为边界域。综合以上两点给出基于有序多属性概率粗糙集的相关基本定义。

定义1 设对象集X⊆U，对∀xi，xj∈X，在某一属性r下，存在xi不劣于xj，则可记为存在xi绝对优于xj，则可记为⊆R，使得

关于属性集P支配xj。

定义2 设P⊆C和x∈U，记x的P支配集为(x)，表示其有序优势关系;记x的P被支配集为Dp(x)，表示其有序劣势关系，表示为：

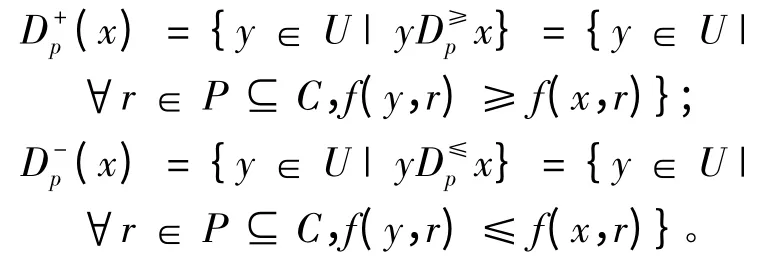
定义3 对于决策属性D，n个不同属性值VD将U中对象分成为n个决策类D={Di，i∈I}，I={1，2，…，n}，则对象中的任意x∈X⊂U属于一个且仅属于一个决策类Di∈D，且Di是有序的，假定∀r，s∈I，若r＞s，则决策类Dr中的元素优于决策类Ds中的对象。

简言之，决策属性D的划分代表论域U中对对象的综合评价，即将最具优势对象置于D1中，最具劣势对象置于Dn中，其他对象则按照“优劣”顺序放置于Di中，i由小到大有序排列。例如，航空灾害预警级别决策规则中，存在I={1，2，3，4，5}，D={D1，D2，D3，D4，D5}，其中D1为无警类，D2为轻警类，D3为中警类，D4为重警类，D5为巨警类。

定义4 对i∈I，I={1，2，…，n}，分别定义i决策类的高势集与低势集：

定义5 设决策知识系统S=(U，C∪D，V，f)，其条件属性和决策属性的等价关系为IND(C)和IND(D)。若IND(C)⊆IND(D)，则该决策知识系统是协调的，否则为不协调。

定义6 设决策知识系统S=(U，C∪D，V，f)，U为非空有限论域，对∀X，Y⊆U，集合X关于集合Y的错误分类率称为E(X，Y)，表示为：

(1)E(X，Y)=1 -(|X∩Y|/|X|)，|X|，且系统不协调;

(2)E(X，Y)=0，|X|，系统协调，即X。

定义7 设决策知识系统S= (U，R，V，f)，∀X，Y∈U，β 为错误分类参数，0≤β ＜0.5，则β包含关系⊆β为X⊆βY⇒E(X，Y)≤β。且 对∀X∈U，X的β-下近似集、上近似集及边界域分别表示和定义为：

(1)X的β -下近似集(X)=U{［x］R|E(［x］R，X)≤β};

(2)X的β -上近似集(X)=U{［x］R|E(［x］R，X)＜1 -β};

(3)X的β-边界域bnβ(X)=U{［x］R|β ＜E(［x］R，X)≤1 -β}。

错误分类参数β 的设置，一定程度上扩张了下近似集的边界，使得规则获取变得更为灵活。

2.2 改进式绝对有序多属性概率粗糙集的定义

在决策知识系统中，不存在有序属性集中每个属性值在不同对象中全部处于有序的优势，用数学表达式在决策知识系统S=(U，C∪D，V，f)中表示这种全部有序优势即为：设对象xi∈U，ck∈C，若对象xi可支配对象xj，则必然∃cm∈C，使得同时∀cn∈C也必须满足同理劣势也类似这样表述。

但是在现实预警决策过程中，基于这样的完全有序优势或完全有序劣势所提取出的规则更为有效。因此，基于上述定义将有序优势关系(x)与有序劣势关系(x)拓展为一种绝对的有序关系，分别定义为绝对有序优势关系和绝对有序劣势关系。

其中n≠k。

定义9 记绝对有序优势等价关系为R+;绝对有序劣势等价关系为R-，分别满足：

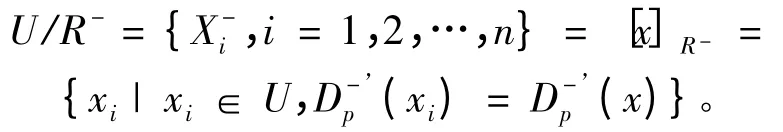
可见，这两种等价关系U/R+和U/R-对U构成了一种全新划分。在数据分析处理中，取代原来的有序关系，使用这种基于绝对有序构成的新划分，使得决策规则提取过程更精细。且可以确定X的判定准则，当X⊆U/R+，X若满足若满足

定义10 设U为非空有限论域，绝对有序优势等价关系为R+;绝对有序劣势等价关系为R-，则：

基于绝对优势关系下，R+关于集合D的错误分类率为：

(2)当|R+| =0 时，E(R+，)=0。

基于绝对劣势关系下，集合R-关于集合的错误分类率为：

(1)当|R-| ＞0 时，E(R-，)=1 -(|R-

(2)当|R-| =0 时，E(R-，Di＜)=0。

在决策知识系统中，不存在有序属性集中每个属性值在不同对象中全部处于有序的优势，用数学表达式在决策知识系统S=(U，C∪D，V，f)中表示这种全部有序优势即为：设对象xi∈U，ck∈C，若对象xi可支配对象xj，则必然∃cm∈C，使得同时∀cn∈C也必须满足xiO≥cn xj，同理劣势也类似这样表述。

2.3 基于改进式绝对有序多属性概率粗糙集的演算过程

在数据抽取、预处理和转换之后形成决策表，令决策表中论域为U，决策属性为D，条件属性集为C，再通过粗糙集的基本定义和知识求得决策类的高低势集，如再通过求得绝对有序优势关系和绝对有序劣势关系得出基于绝对优势关系下R+关于集合的错误分类率和基于绝对劣势关系下集合R-关于集合的错误分类率，求得错误分类率β 情况下的分类情况，再通过定义9 中的判定准则可得到在β 情况下所有对象的判定结果，从而推导出预警规则。

其演算过程如图4 所示。

2.4 基于改进式绝对有序多属性概率粗糙集的航空灾害协同预警应用

笔者根据航空灾害系统预警所形成的决策系统分析，将航空灾害协同预警指标体系和航空灾害预警级别的数据通过数据预处理和转换，并将航空灾害协同预警指标体系看作条件属性集Ci，其中i=1，2，…，n，将航空灾害预警级别看作决策属性D，选择需要分析的航空灾害数据作为论域U，根据以上的绝对有序多属性概率粗糙集的定义和演算过程求得航空灾害协同预警规则，并通过系统功能及时反映在预警系统中，给相关人员提供预警信息，做出预警措施。

图4 绝对有序多属性概率粗糙集的演算过程

3 实例分析

3.1 数据准备

考虑到航空灾害协同预警指标体系中指标较多，兼顾粗糙集决策方法中决策表过大，则需要借助计算机实现计算之特性，笔者主要依据调研、搜集整理获得航空灾害数据，从图1 中的航空灾害协同预警指标体系中抽取部分重要及常见指标，如图5 所示，构成演算协同预警指标体系。

图5 实例演算预警指标体系

融合航空灾害预警级别数据形成航空灾害预警决策表，确定12 例航空灾害事件(其中10 例为真实剥离数据，2 例为极端假设对象)，并最终通过数据离散化和不完备信息完整化处理，实例演算决策表如表2 所示。

表2 实例演算决策表

论域U中数据确定条件属性集C对应决策属性D，其中决策属性D表示航空灾害预警级别，其取值分别为无警、轻警、中警、重警和巨警。条件属性集C中的1、2、3 分别表示各个属性的值域，即各个指标的低、中、高，记为：

决策属性D中的1、2、3、4、5，分别表示无警、轻警、中警、重警和巨警，记为：

3.2 绝对有序多属性概率粗糙集实例运算

根据绝对有序多属性概率粗糙集方法的演算过程，提取最终规则步骤如下：

(1)论域U在决策属性D下可分为：

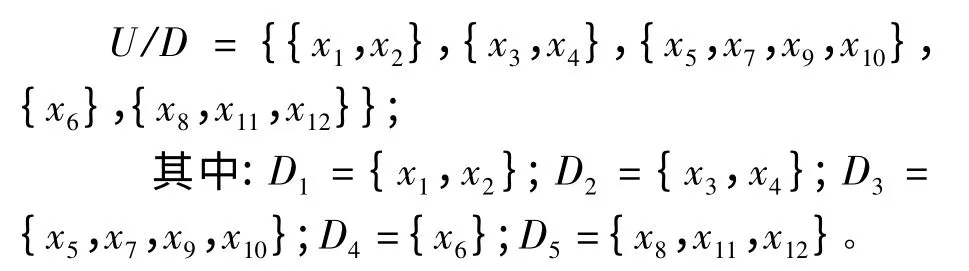
(2)D1、D2、D3、D4、D5的高势集与低势集：

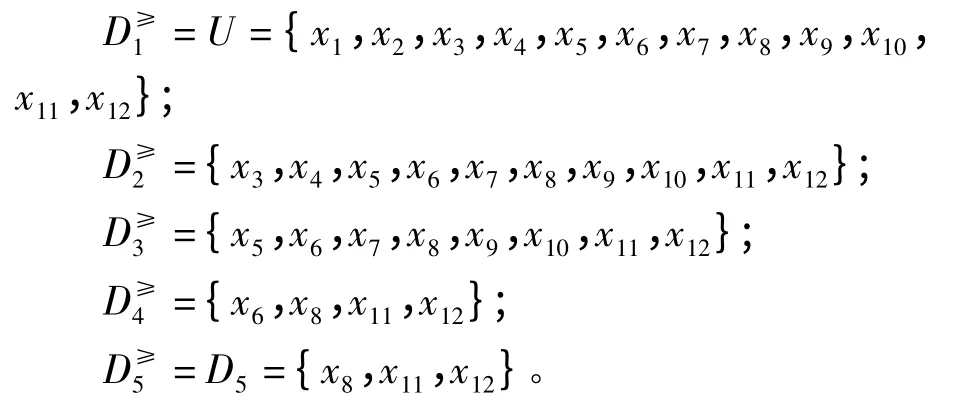
(3)论域U在条件属性C下可划分为：

其中：X1= {x1};X2= {x2，x3};X3= {x4};X4={x5};X5={x6，x7，x8};X6={x6};X7={x7};X8={x8};X9={x9}。

(4)对象集U中x1，x2，x3，x4，x5，x6，x7，x8，x9，x10，x11，x12各自的绝对有序优势关系和绝对有序劣势关系D-’

C(xi)如下所示。

其中，绝对有序优势关系如下：

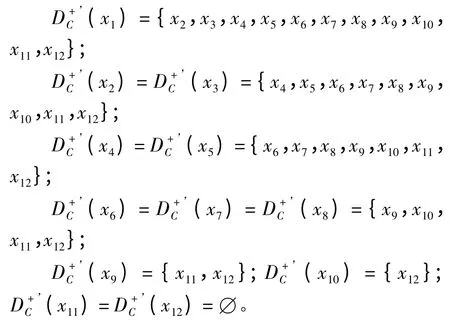
绝对有序劣势关系如下：

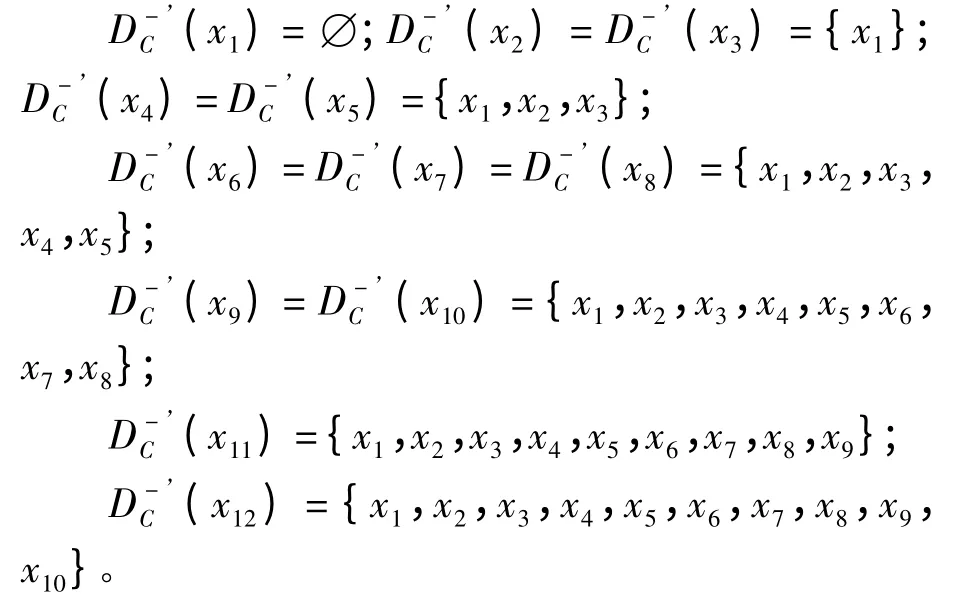
(5)得到绝对有序优势等价关系U/C+和绝对有序劣势等价关系U/C-。

表3 E(，)计算表

表3 E(，)计算表

E(X +i ，D≥j ) D≥1 D≥2 D≥3 D≥4 D≥5 X +1 0.00— —X +2 0.000.50— —X +3 0.000.000.50— —X +4 0.00 0.00 0.00 0.33 0.67 X +5 0.000.000.00— —X +6 0.000.000.00— —X +7 0.00 0.00 0.00 0.00 0.00

表4E(，)计算表

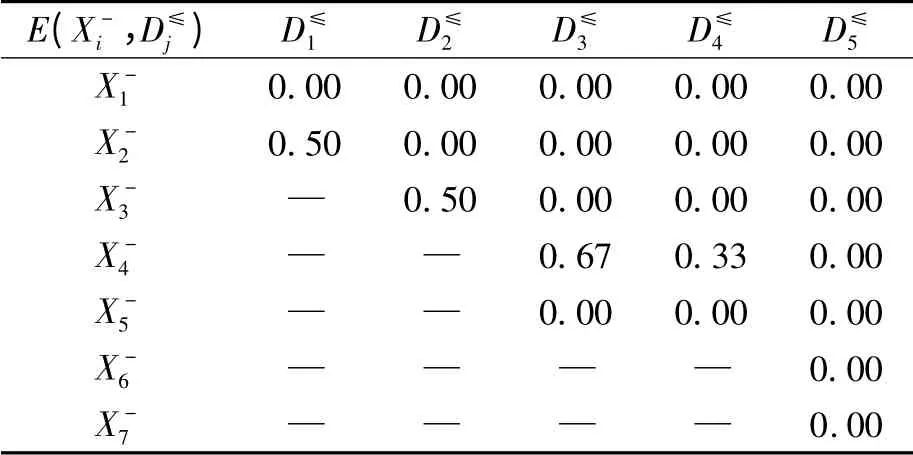
表4E(，)计算表

注：“—”表示不存在

E(X -i ，D≤j ) D≤1 D≤2 D≤3 D≤4 D≤5 X -1 0.00 0.00 0.00 0.00 0.00 X -2 0.50 0.00 0.00 0.00 0.00 X -3— 0.50 0.00 0.00 0.00 X -4——0.670.330.00 X -5——0.000.000.00 X -6——0.00 X -7 0.00——

3.3 决策分析

在表2 的现有数据环境下，可以推导出以上规则，转换成语义分析表达。

(1)机长违规操作率为低，天气恶劣程度为低，且非法行为危害指数为低时，系统做无警决策，其精确率为1，系统提示为可正常运行。

(2)机长违规操作率为低，天气恶劣程度为中，且非法行为危害指数为低时，系统做无警或轻警决策，不显示预警信号或者蓝色预警信号，其精确率为0.5。但根据灾害发生的危害性，可预设系统在无法正确决策的情况下选择有序劣势决策。因此系统正常情况下显示蓝色预警信号，但行为人(机长、机组或空管人员)可根据实际情况更改预警决策。

(3)机长违规操作率为中，天气恶劣程度为中，且非法行为危害指数为低时，系统做轻警决策，显示蓝色预警信号，其精确率为1，机长需根据系统提示规范其操作规则，避免预警决策升级。

(4)机长违规操作率为中，天气恶劣程度为中，且非法行为危害指数为中时，系统可能做中警、重警和巨警决策，精确率为0.3。

(5)机长违规操作率为中，天气恶劣程度为高，且非法行为危害指数为中时，系统做重警决策，显示橙色预警信号，其精确率为1。

(6)机长违规操作率为中，天气恶劣程度为高，且非法行为危害指数为高时，系统做重警决策，显示橙色预警信号，其精确率为1。

(7)机长违规操作率为高，天气恶劣程度为中，且非法行为危害指数为高时，系统做巨警决策，显示红色预警信号，其精确率为1。

(8)机长违规操作率为高，天气恶劣程度为高，且非法行为危害指数为高时，系统做巨警决策，显示红色预警信号，其精确率为1。

以上获得的8 条预警规则是系统基于小数据量的统计分析获得的。从航空灾害致灾成因角度上讲，这些规则较少且略显粗糙。但从系统角度上说，航空灾害协同预警可将所有协同预警指标体系和航空灾害预警级别全部纳入其中，再将基于绝对有序多属性概率粗糙集方法转换为程序输入系统，运用计算机系统超强的计算能力，快速分析获得更为有效的预警规则。

4 结论

(1)提出了一种基于绝对有序多属性概率粗糙集航空灾害协同预警模型，对航空灾害协同预警中所涉及到的航空灾害协同预警指标和航空灾害预警级别数据进行科学分析，抽取出数据中所蕴含的数据特性，如作为条件属性的航空灾害系统预警指标中的有序性(高、中、低);如作为大数据中所存在的大量不相容，即相同的协同预警指标可能产生不一样的航空灾害预警级别等特性。

(2)采取绝对有序多属性概率粗糙集方法进行计算，有效规避了航空灾害数据所存在的不相容和有序两种特性给协同预警带来的不准确，最终提取更为准确有效的预警规则，使得航空相关人员或组织做出有效对策防止航空灾害事件的再次发生。

［1］周育健，王钰.RSL：基于Rough Set 的表示语言［J］.模式识别与人工智能，1996，9(8)：570 -575.

［2］刘清.Rough 集及Rough 推理［M］. 北京：科学出版社，2001：201 -209.

［3］曾黄麟.粗集理论及其应用［M］.重庆：重庆大学出版社，1998：43 -89.

［4］何先华，赵卫东，盛昭瀚.粗集在医疗诊断知识支持中的应用［J］.计算机工程与应用，2001(20)：166-168.

［5］苗夺谦，王钰.知识粗糙性的信息论解释［C］∥1996年中国智能自动化学术会议论文集. 北京：中国科学院自动化研究所，1996：154 -160.

［6］刘盾，李天瑞. 区间决策粗糙集［J］. 计算机科学，2012(7)：178 -181.

［7］刘盾，李天瑞.模糊数决策粗糙集［J］.计算机科学，2012(12)：25 -29.

［8］史开泉，崔玉泉.S-粗集和它的生成结构［J］.山东大学学报：理学版，2002(6)：471 -474.

［9］张文修，吴伟志.粗糙集理论与方法［M］. 北京：科学出版社，2001：65 -132.

［10］史开泉，崔玉泉.S -粗集和它的分解还原［J］. 系统工程与电子技术，2005(4)：644 -651.

［11］王国胤.Rough 集理论与知识获取［M］.西安：西安交通大学出版社，2001：1 -226.

［12］刘清，刘少辉，郑非.Rough 逻辑及其在数据约简中的应用［J］.软件学报，2001，12(3)：415 -419.