飞机路线多目标决策研究

乐美龙，黄翠萍

(1.上海海事大学 科学研究院，上海201306;2.上海海事大学 物流研究中心，上海201306)

飞机路线就是将一组飞机分配给一个航班集以产生能满足市场需求的日常航班调度［1］。在全球范围内，关于飞机路线方面的研究早已形成一套完整体系。在文献［2］中，CLARKE 等将飞机路线问题看成是带有侧约束的欧拉回路问题，实质就是旅行商问题，顺带研究了两者之间的相似之处，并利用拉格朗日松弛使计算变得简单。在文献［3］中，GOPALAN 等也将飞机路线问题看成是欧拉回路问题。而在文献［4］中，CORDEAU等认为，飞机路线是一个航空资源分配的问题，是一个非线性的资源约束的多商品流网络设计问题，由于约束之间相互关联，其采用了Benders 分解。在文献［5］中，MERCIER 等也将飞机路线问题看成是多商品流网络设计问题，在改进模型的基础上增强了调配方案的鲁棒性，与CORDEAU不同的是，MERCIER 根据问题的主次采用了两种Benders 分解方法，具有较强的对比性。

1 航班环的生成方法

飞机路线问题的关键就是航班环的生成，人工完成这项工作非常耗时和疲惫，但是利用计算机来完成却非常省时快捷。具体的计算机运行步骤如下：

(1)输入所有航班的航班号、离港和进港城市及时间。

(2)生成所有可能周期为一日的有效飞机路线调配方案(航班串)，并设定地面过站时间最小为1 h，一天之内一航班串的总的时间不得超过12 h，将结果存入一个文件夹。

(3)把这个文件中的每一个航班串与其文件中的所有航班串按照过夜机场与下一天的起飞机场相同的原则连接起来。该步骤重复两次即可得到周期为三日的航班环，需要注意的是，所有航班环的起始机场和终止机场相同，并且至少在中心机场过夜一次。

2 飞机路线调配模型

设置飞机路线调配模型的参数：Tsk为第sk个航班的总的飞行时间;Msk为第sk个航班环在中心城市过夜的次数;Csk为第sk个航班环的飞行成本;Fc为被覆盖的航班数;F为总的航班数。

决策变量：

目标函数：

飞机利用率最大化，即maxxsTsk

维修机会最大化，即maxxsMsk

飞机数量最小化，即minxs

飞行总成本最小化，即minxsCsk

航班覆盖率最大化，即maxFc/F

3 模型的求解

3.1 染色体设置

染色体的设置方法很多，为了简化运算，采用二进制编码［6］。

一共有S个航班环可供选择，则可以把S个航班环看成是S个遗传因子，构成一个染色体，编码为1 表示选择了该航班环，代表显性基因，编码为0 表示未选择该航班环，代表隐性基因。

初始化设置：进化代数进化器t=0，最大进化代数T，随机生成M个个体作为初始种群P(0)。

3.2 适应性函数设置

根据模型特点，主要有5 个目标函数，因此是一个多目标规划问题。单纯使用权重的方法不是很合适［7］，在这里采用ELECTRE -IV 来评价个体的适应度。ELECTRE -IV 相对于ELECTRE -I、ELECTRE -II 和ELECTRE -III 而言，最大的特点就是不设定表示属性相对重要性的权［8］。

首先，确定各个目标j下的无差别阈值qj，严格优于阈值pj，否决阈值vj，一般满足qj＜pj＜vj。阈值的确定原则可参考文献［9］，如表1 所示。

表1 各目标属性值下的阈值

其次，根据式(1)和式(2)计算目标属性的集合。其中，J+(ai，ak)为个体ai优于ak的目标属性的集合，J-(ai，ak)为个体ai劣于ak的目标属性的集合，cij为目标属性j下的个体i的属性值。然后，根据式(3)和式(4)确定个体之间强级别高于关系Os和弱级别高于关系Ow。

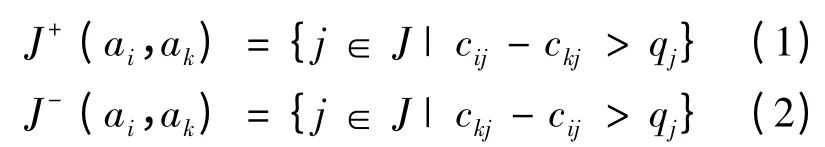
表2 所示为M个个体之间的优劣比较结果的直观表示。a1行和a2列对应的是Ow，则说明a1劣于a2，是a1Owa2的直观表示。那么反过来，a2就应该优于a1，即为a2Osa1的直观表示。

表2 个体之间的级别高于关系

最后，根据表2 的级别高于关系，得出排序结果，如表3 所示。

表3 排序结果

根据整个种群在考虑5 个目标属性上的总排序，确定适应性函数。

3.3 选择

将经过适应度评价的个体按照一定的概率筛选。将种群中M个个体按照适应度从大到小排列，由于笔者在选择过程中采用的是精英策略［10］，因此前10%的个体按P=1 的概率直接复制到下一代，将下一代的后10%替换掉，以保持种群数量不变。

3.4 交叉配对

随机将两个父代个体进行交叉运算生成新的个体。交叉运算原则可用以下矩阵运算规则表示：

若新的个体的显性因子较多，那么，不可避免地会出现不可行解(有航班同一天内被覆盖两次及两次以上)，这就需要将同一天内覆盖同一航班的众多航班环按照随机抽取的原则，随机选择一个航班环，去掉其他的航班环，将其修正为可行解。

3.5 变异运算

若个体中两个父代配对以后不按上述矩阵运算规则产生子代，则为变异。

3.6 终止原则

按照适应性函数的设置，选择、交叉配对，如此循环，直到进化代数进化器t=T，最后一个种群为P(t)。在所有临时最优解中寻找最优作为该模型的近似最优解。

4 算例

以东方航空的波音737 机型的北京、上海、南京、广州、成都、昆明的航班时刻表(表4)为例，一共是22 个航班。

(1)对表4 航班时刻进行规范处理，利用Matlab 编程，按照上述的要求，生成周期为一天的航班串，最多为4 个航班，共有85 个航班串。

(2)利用Matlab 生成周期为3 日的航班环。但是，考虑到现实中3 天飞两个航班以及覆盖率问题，可考虑在航班串中加入这22 个航班以及符合3 天飞两个航班的航班环，为696 个。

(3)按照改进遗传算法的步骤，设定种群M=100，遗传因子S=696，交叉配对的概率0.6，变异的概率0.1，部分结果如下：

表4 航班时刻表

在这个算例中，经过500 次迭代，最终选出了9 个航班环，即只需要9 架飞机来执行所有的航班，但是对S444，S452，S458和S468这4 个航班环的航班可作适当的调整。总飞行成本如图1 所示。

由图1 可知，总的飞行成本由大变小，最后趋于稳定。经过近300 代以后，收敛于一固定成本，主要是各个目标互相牵制作用的结果，虽然过程此起彼伏，但是最终结果趋向于能兼顾各目标的一个成本，即成本的增加已不能使其他目标更加优化。

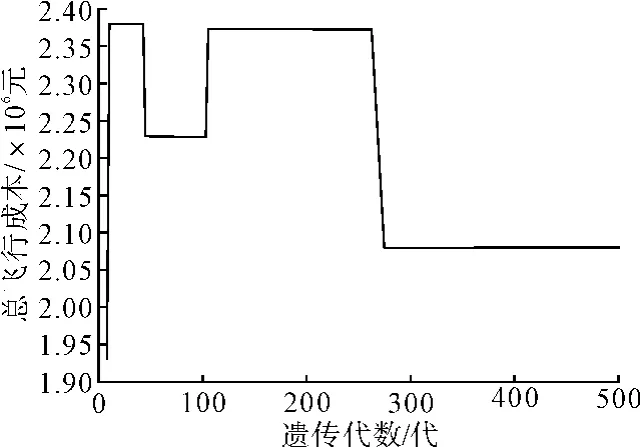
图1 总飞行成本

5 结论

笔者结合ELECTRE-IV 和改进遗传算法来研究飞机路线规划，具有计算速度快、时间短的优势，但也有不足之处，例如航班环的数量过大，以及如何快速收敛到近似最优解等，只有解决了这些问题，才能使飞机路线规划在实际使用的效率和速率上得到令人满意的结果。

［1］CHOU T Y，LIU T K，LEE C N，et al.Method of inequality-based multiobjective genetic algorithm for domestic daily aircraft routing［J］.IEEE Transactions on Systems，Man，and Cybernetics(Part A：Systems and Humans)，2008，38(2)：299 -308.

［2］CLARKE L，JOHNSON E，NEMHAUSER G，et al.The aircraft rotation problem［J］. Annals of OR：Mathematics of Industrial Systems II，1997，69(1)：33-46.

［3］GOPALAN R，TALLURI K. The aircraft maintenance routing problem［J］. Operations Research，1998(46)：260 -271.

［4］CORDEAU J，STOJKOVIC G，SOUMIS F，et al.Benders decomposition for simultaneous aircraft routing and crew scheduling［J］. Transportation Science，2001(35)：375-388.

［5］MERCIER A，CORDEAU J，SOUMIS F.A computational study of benders decomposition for the integrated aircraft routing and crew scheduling problem［J］. Computers ＆Operations Research，2005，32(6)：1451-1476.

［6］沈中林，李廷朵. 遗传算法在航班覆盖问题中的应用研究［J］.中国民航大学学报，2008，26(6)：5 -9.

［7］游进军，纪昌明. 基于遗传算法的多目标问题求解方法［J］.水利学报，2003(7)：64 -69.

［8］孙世岩，邱志明. 级别不低于方法及其发展评述［J］.管理工程学报，2008，22(3)：41 -45.

［9］LIU P D，ZHANG X.Research on the supplier selection of a supply chain based on entropy weight and improved ELECTRE-III method［J］.International Journal of Production Research，2011，49(3)：637 -646.

［10］李耀华，秦如如.基于混合遗传算法的航班串优化模型研究［J］.中国民航大学学报，2010，28(6)：31-34.