基于库存成本视角的供应链VMI 利益分配

谭 洁，郑 齐，林 强

(1.上海交通大学 中美物流研究院，上海200030;2.天津大学 管理与经济学部，天津300072)

1 文献综述

利益分配问题已成为影响双方合作实施供应商管理库存(vendor managed inventory，VMI)的重要因素［1］。杨怀珍等［2］通过对比分析供需方在传统库存模式与VMI 模式下的经济效果模型，认为VMI 可使供应链上游层面整体受益。但在具体实践中供需双方容易出现责任与利益不一致的现象，因此有必要建立起合理的利益分配机制［3］。在利益协调机制具体设计的研究中，价格契约和收益分享契约是经常运用的两种契约。钟磊钢等［4］针对有确定需求、有初始库存和库存短缺的一种畅销商品，建立了数量折扣契约的激励机制来协调VMI环境下供应商和零售商的收益。YU 等［5］的研究表明只要零售商能够与供应商合作，接受一个按一定比例分享增加利益的契约，就能使Stackelberg 博弈均衡得到进一步改善，提高双方的收益。

VMI 策略下供需双方利益变化的一个重要体现是各自库存成本的改变，但目前较少有专门从库存成本角度研究利益分配问题。BERNSTEIN等［6］将VMI 模式分为VMI+和VMI-两种类型。通过分析供需双方库存成本变化可以发现，在VMI-模式下，零售商通过将库存成本转移到供应商实现利润增长，供应链也会因为库存成本下降而增加收益，但供应商在承担零售商库存成本后的收益变化却不确定，这说明在VMI-模式下，实施VMI 总是对买方有利，但供应商能否获利尚不确定，DONG［7］和YU 等［8］运用演化博弈理论方法得出了类似的结论。因此，有必要从库存成本角度建立利益分配机制，以协调供需双方因库存成本变化而产生的损益。

鉴于此，笔者在分析实施VMI 前后库存成本变化的基础上，建立起零售商强势情况下短期VMI 利益分配模型，对于建立稳定的供需合作关系具有较好理论价值与现实意义。

2 模型假设和参数说明

2.1 模型假设

(1)供应链由一个零售商和一个供应商组成，且零售商处于强势地位。

(2)供应商和零售商均不考虑缺货成本。

(3)供应商和零售商存在安全库存。

(4)实施VMI 之前零售商库存成本包括维持成本、订货成本和运输成本。

(5)实施VMI 之前供应商库存成本包括维持成本和订货成本。

2.2 参数说明

模型中的参数说明如下：D为零售商的年度需求量;Cr为实施VMI 之前零售商的库存成本;Cs为实施VMI 之前供应商的库存成本;C'r为实施VMI之后零售商的库存成本;C's为实施VMI 之后供应商的库存成本;ω 为实施VMI 之前零售商的采购价格;ω'为实施VMI 之后零售商的采购价格;Hr为零售商单位库存维持成本;Hs为供应商单位库存维持成本;Sr为零售商订货成本;Ss为供应商订货成本;t为商品运输成本;SSr为实施VMI 之前零售商的安全库存;SSs为实施VMI 之前供应商的安全库存;SS为实施VMI 之后供应商的安全库存。

3 实施VMI 前后供应链库存成本模型

3.1 实施VMI 之前的供应链库存成本

实施VMI 之前，零售商与供应商各自设立并管理库存，因此二者均需承担库存成本。

在不考虑缺货成本的前提下，零售商的库存成本如式(1)所示：

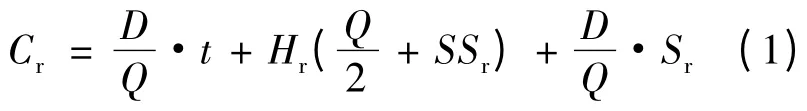
式中：第一项为运输成本;第二项为维持成本;第三项为订货成本。根据EOQ 模型，可知零售商的经济订货批量此时零售商的库存成本达到最优，如式(2)所示：

在实施VMI 之前，若不考虑缺货成本，则供应商库存成本由维持成本与订货成本两部分构成，如式(3)所示：

在零售商强势情况下，供应商必须满足零售商的经济订货批量，因此，此时供应商的库存成本为：

假定零售商从供应商手中订购的货物最后全部出售给消费者，那么零售商的年需求量与供应商的年需求量是相等的［9］。此时，供应链的最优库存总成本即为供应商与零售商经济订货批量策略下的库存成本之和，由式(2)和式(4)可知，实施VMI 之前供应链的库存总成本为：

3.2 实施VMI 之后的供应链库存成本

实施VMI 以后，由供应商负责将产成品运送到零售商处，零售商不再承担运输成本。同时，供应商还要负责零售商的库存管理，制定库存策略，并确定经济订货批量、库存水平等，零售商的维持成本和订货成本也就转移到供应商，供应商的单位维持成本变为Hr+Hs，单位订货成本变为Sr+Ss。

由于实施VMI 以后，零售商不再需要承担库存，其运输成本、维持成本、订货成本等都转移到供应商，因此其库存成本为零。

考虑到实施VMI 后，供应商与零售商的协调水平将会上升，能够降低库存成本，因此定义k为实施VMI 后的库存管理协调系数，表示供应链库存协调水平(k越大，供应链协调水平越高)，且0≤k＜1。

由于实施VMI 后零售商库存为零，因此供应商的库存成本也就是供应链的整体库存成本。

式中：第一项为运输成本;第二项为维持成本;第三项为订货成本。可以看出k与TC'负相关，k越小，库存成本就越高。对式(6)求关于Q'的一阶条件，可以得到经济订货批量Q'=

同样根据EOQ 模型，将实施VMI 后的供应商经济订货批量Q'代入式(6)，即可得到供应链最优库存成本：

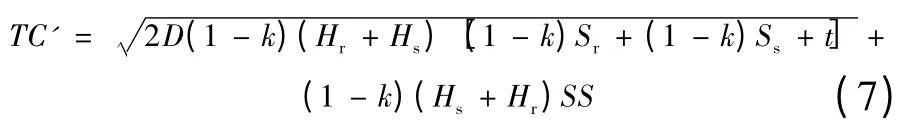
假设实施VMI 后短期内市场无较大波动，需求量D无明显变化，满足短期定义的内涵［10］，则实施VMI 前后供应链总库存成本变化为：

式(8)中的第一项，上述已经说明，实施VMI以后供应链库存成本与供应链库存协调水平负相关，具体来说，就是供应链库存协调系数k越小，供应链协调水平越低，库存成本就越高。不妨取极值进行考虑，令k=0，此时供应链库存成本最大，第一项可简化为因此第一项恒大于等于零。对于式(8)的第二项，安全库存SS=zσ，其中，z为安全系数，σ 为需求标准差，L为提前期。实施VMI 以后，由于供应链协调水平提高，提前期将会缩短，因此SSr＞SS，又因为供应链库存协调系数k满足0 ＜k≤1，所以第二项大于零。对于式(8)的第三项，实施VMI 以后供应商直接管理零售商库存，因此其需求偏差将会减小，所以SSs＞SS，又0 ＜k≤1，同理可得出第三项大于零。由此可见，实施VMI 以后，供应链库存成本变化总是大于零。

综上所述，可以看出：实施VMI 以后供应链整体库存成本与零售商库存成本均会下降，并且供应链库存管理协调水平越高，供应链整体库存成本下降越多。

4 实施VMI 后供应链利益分配模型

4.1 实施VMI 前后供需双方利益变化

实施VMI 以后，零售商的库存成本转移到供应商，库存成本变为零，因此实施VMI 前后其库存成本变化即为实施VMI 之前的库存成本。

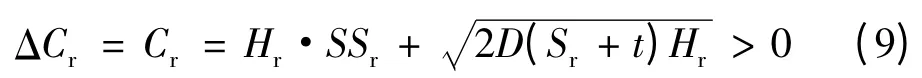
在实施供应商管理库存前后，由式(4)和式(6)可知，供应商库存成本变化为：

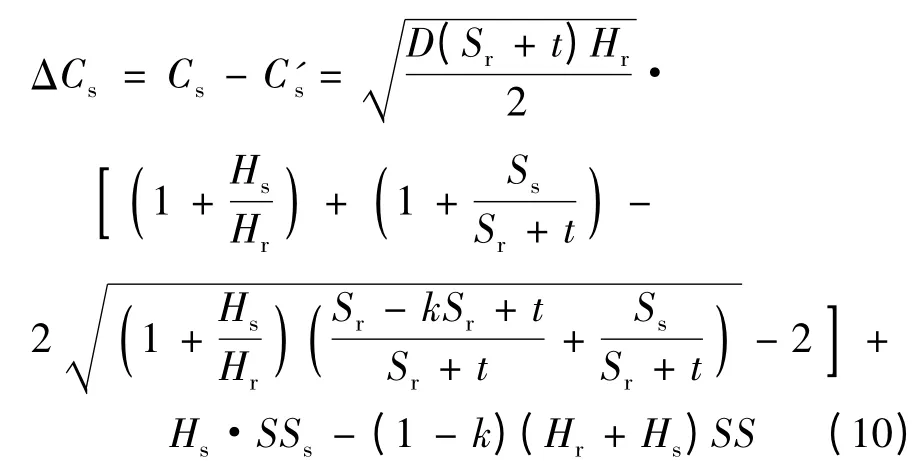
从式(10)中无法明显看出供应商库存成本的下降趋势。事实也是如此，在短期内，实施VMI以后供应商库存成本不一定降低，相反由于额外承担了零售商的运输成本、维持成本，以及订货成本，其库存成本还有可能提高。

根据短期定义，VMI 实施短期内市场需求和价格都将保持不变。那么实施VMI 前后零售商的利润函数分别如式(11)和式(12)所示：

式(13)说明，零售商能够从实施VMI 过程中获取利益，这是因为在实施VMI 以后零售商的库存成本转移到了供应商，因此利润会有所上升。

若实施VMI 之后零售商的采购价格与实施前保持一致，则供应商的利润变化也与其库存成本变化相一致，如式(14)所示：

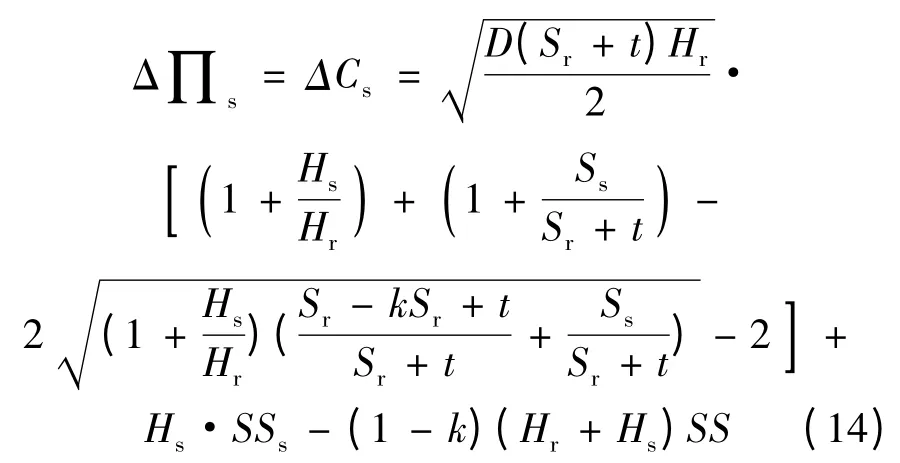
从式(14)中并不能明显看出供应商的利润增长。这是因为短期内零售商订货批量受市场约束并不会立刻显著增加，所以其利润增长不能明显看出，甚至还有可能下降。

综上所述，实施VMI 后，零售商通过转移库存成本能够获取较大利润，而供应商虽然承担了零售商的库存成本，却并没有从供应链整体库存成本下降所带来的利润中受益，这说明：在实施VMI 短期内，供需双方会形成较为明显的责任与利益不一致的情况。该情况将会严重影响供应商实施VMI 的积极性，因此零售商有必要通过调整采购价格来补偿供应商的利益，以激励供应商积极参与到VMI 的构建过程中来。

4.2 零售商强势情况下的利益分配模型

在构建VMI 的过程中，零售商可通过提供较高的采购价格来激励供应商，以提高其积极性。若供应商和零售商双方实现信息共享，则契约制定过程可看成是二人Stackelberg 博弈，零售商是领导者，供应商是追随者。博弈过程描述如下：

(1)假定双方对VMI 实施后的预期收益都为VMI 实施前的最大利润值。只有当VMI 实施后双方的利润都不少于其预期收益，协议才能达成，否则双方的收益均为VMI 实施前的最大利润值。

(2)博弈首先由零售商提出新的采购价格ω'，对该价格，供应商可以接受或者拒绝，供应商做出决策后博弈结束。

(3)若供应商接受零售商提出的协议价格，则VMI 得以实施。

上述Stackelberg 博弈的Nash 均衡为在保证实施VMI 后供应商利润不少于实施VMI 之前的前提下零售商利润最大化。

笔者假定在供应链中零售商处于强势地位，供应商只能被动接收零售商提供的采购价格，那么在实施VMI 之前，零售商可以通过调整采购价格来使供应商接受其采购数量，并实现双方利润最大化。

在实施VMI 之前，供应商利润函数如下：

式中：∏s为供应商利润函数;ω 为零售商采购价格;g为商品单位生产成本;最后一项为供应商最优库存成本。求式(15)关于需求量D的一阶条件，可以得到：

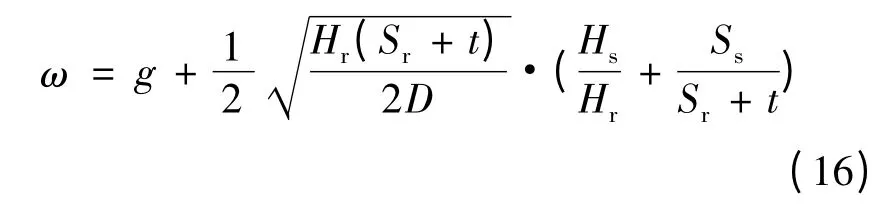
从式(16)可以看出，对于零售商给定的采购价格，供应商会通过调整供货量D来实现自身利润最大化。也就是说，零售商可以通过调整采购价格，使之满足式(16)，来保证供应商供货量与自身订货量匹配，此时，供需双方均实现了利润最大化。

实施VMI 后，零售商库存成本转移给供应商，其利润来源于销售价格与采购价格之差。由于短期内p(D)保持不变，因此零售商利润最大化问题可以转化为求解VMI 环境下采购价格ω'的最小值问题，即：

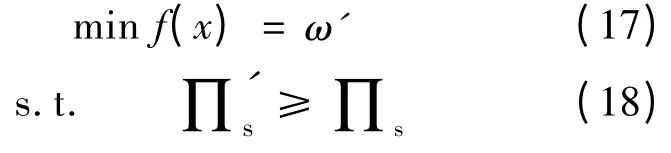
在实施VMI 前后，供应商的利润变化主要来源于零售商采购价格与供应商自身库存成本的变化，则式(18)可以改写为：

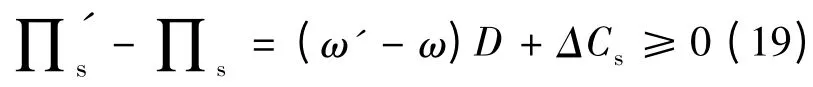
将式(10)和式(16)代入式(19)，即可推出实施VMI 后零售商应该给予供应商的激励价格为：

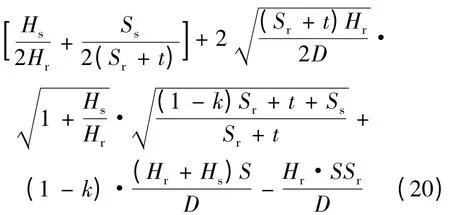
在该价格下，供应商实施VMI 之后的利润将不小于实施VMI 之前，这就可以较好地调动供应商实施VMI 的积极性，有助于在供应商与零售商之间构建VMI，从而零售商也可以通过实施VMI转移库存成本，实现利润增长，最终实现供应商与零售商“双赢”的局面。

从式(20)可以看出，ω'与项1 -k正相关，也就是说，随着供应链库存管理协调系数k的增大，零售商采购价格ω'将会下降。这说明：零售商为实施VMI 所应给予供应商的激励价格随着供应链库存协调水平的上升而减小。

总之，强势零售商要通过合理调整采购价格，建立起合理的利益分配机制，对供应商因实施VMI 所承担的零售商库存成本做出利益补偿，这样才能建立稳定的供需合作关系，提高供应链的整体竞争力。

5 算例分析

假定供应链中存在供应商A 与零售商B，并且在合作关系中零售商B 处于主导地位。双方经过协商，确定对某一商品实施VMI 策略。实施VMI 前供应链参数如表1 所示。

表1 实施VMI 前供应链参数表

将需求与标准差转化为以周为单位(每月按4 周计算)，则零售商平均每周需求为400，平均每周标准差为22.64，在服务水平为97%条件下，对应安全系数为1.88，故零售商安全库存为60(商品数量为一正整数)。同理可以计算出实施VMI之前供应商的安全库存为75。

根据EOQ 模型，可知零售商经济订货批量为131。由式(5)可知实施VMI 前供应链库存成本为84 165.9 元，根据式(16)可以求出此时零售商应该提供给供应商的采购价格为878.7 元。

实施VMI 之后，假设供应链库存管理协调系数k为0.6，供应商安全库存为48(小于实施VMI之前的供应商与零售商安全库存)，可以求出此时供应商经济订货批量为118，根据式(7)可以知道供应链库存总成本为31 580. 0 元，小于实施VMI 之前的84 165.9 元，说明实施VMI 之后供应链库存成本将会下降。根据式(20)可知，此时零售商为实施VMI 应该给予供应商的激励采购价格为900.5 元。

进一步，保持其他参数不变，将供应链库存管理协调系数k调整为0.8，可以求得该条件下，供应链库存总成本为17 370.2 元，零售商应该给予供应商的激励采购价格为880.3 元。两种k值情况下供应链各参数对比如表2 所示。

表2 两种k 值情况下供应链参数表

从表2 可以看出，在供应链库存管理协调系数k上升后(由0.6 变为0.8)，供应链库存成本与零售商激励价格均有下降趋势，由此证明：在实施VMI 后，供应链库存管理协调水平越高，供应链库存成本与零售商激励价格将越低。

6 结论

从库存成本角度切入，对比分析了实施VMI前后供应链库存模型，并进一步研究了供应链协调水平对于库存成本的影响，在此基础上应用价格契约建立了短期内供需双方利益分配模型，对于解决实施VMI 短期内合作双方的责任与利益不统一的问题，具有重要的理论与现实意义。研究还证明实施VMI 后，供应链库存管理协调水平越高，供应链库存成本和零售商激励价格就越低。

［1］王丹.供应链风险下的战略供应商选择方法及利益分配机制研究［D］.大连：大连海事大学图书馆，2008.

［2］杨怀珍，李雷.确定需求时上游层面VMI 利益分配机制研究［J］.工业工程与管理，2011，16(1)：64-69.

［3］曹武军，李成刚，王学林，等.VMI 环境下收入共享契约分析［J］.管理工程学报，2007，21(1)：51 -55.

［4］钟磊钢，胡勇，张翠华.一类供应商管理库存供应链协调策略研究［J］.中国管理科学，2006，14(6)：92-97.

［5］YU Y G，HUANG G Q，LIANG L. Stackelberg game- theoretic model for optimizing advertising pricing and inventory policies in vendor managed inventory(VMI)production supply chains［J］. Computers and Industrial Engineering，2009，57(1)：368 -382.

［6］BERNSTEIN F，CHEN F，FEDERGRUEN A. Coordinating supply chains with simple pricing schemes：the role of vendor - managed inventories ［J］. Management Science，2006，52(10)：1483 -1492.

［7］DONG Y，XU K F. A supply chain model of vendor managed inventory［J］. Transportation Research Part E，2002，38(2)：75 -95.

［8］YU H S，ZENG A，ZHAO L D. An evolutionary model for supply chain partnerships system based evolutionary game［J］. Computers ＆ Industrial Engineering，2009，56(1)：274 - 282.

［9］ANGERHOFER B J，ANGELIDES M C. A model and a performance measurement system for collaborative supply chains［J］. Decis Support Syst，2006，42(1)：283 -301.

［10］DARWISH M A，ODAH O M. Vendor managed inventory model for single-vendor multi-retailer supply chains［J］. European Journal of Operational Research，2010，204(3)：473 -484.