观察法在高等数学教学中的应用
薛利敏
(渭南师范学院数学与信息科学学院,陕西渭南 714099)
观察法在高等数学教学中的应用
薛利敏
(渭南师范学院数学与信息科学学院,陕西渭南 714099)
观察就是仔细察看.观察是进行科学研究的出发点,是一切发明创造的源泉.文章通过实例从顺序观察法、解剖观察法、对比观察法、重点观察法和全面观察法等几个方面介绍了观察法在高等数学教学中的应用,阐明了在高等数学教学中如何培养学生的观察能力.
观察;观察法;观察能力;高等数学教学
1 观察法及其功能
1.1 观察法的概念
观察,从字面上讲,“观”是“看”的意思,“察”是“仔细看”的意思.因此,观察就是仔细察看[1].
在心理学中,观察被看作是一种有目的、有计划、有步骤的感知活动,是一种主动的、对思维起积极作用的感知活动.从方法论上来说,观察是人们通过感官,或借助于一定的科学仪器,对客观对象(数学对象、自然现象、社会现象等)在自然条件下,进行有目的、有计划、有步骤地考察和描述的一种方法[2].
可见,观察是认识主体通过感官对客体的认识过程.所谓观察法就是认识主体通过感官对客体仔细察看,获得信息,经过分析推理去伪存真,找出规律,归纳猜测,得出结论,导致发现的一种方法.
1.2 观察法的功能
俄国著名的心理学家巴甫洛夫指出:“应当先学会观察.不学会观察,就永远当不了科学家.”物理学家法拉第说过:“没有观察就没有科学,科学的发现诞生于仔细的观察中,观察是我们研究问题的出发点.”[2]1665年夏天,伟大的物理学家、数学家牛顿躺在苹果园里,观察苹果熟了之后,就会从树上掉下来,而不会飞向天空,从而得出地球具有万有引力的结论.法国数学家之所以能神速地算出1+2+3+…+100= 5 050,首先是因为他观察到这个算术题的特点,发现了1,2,3,…与100,99,98,…之间某种和谐的对应关系,即1+100=2+99=3+98=…=50+51=101,并且这样的数总共有50对,因此他很容易就得到了答案5 050.很多数学事实,都是先由观察发现的,正如法国著名数学家欧拉所说:“今天人们所知道的数的性质,几乎都是由观察发现的,并且早在用严格论证确认其真实性之前就被发现了,甚至到现在还有许多关于数的性质是我们所熟悉而不能证明的,只是观察才使我们知道这些性质.”[3]事实上,哥德巴赫就是通过对数的观察提出了著名的哥德巴赫猜想.
科学研究离不开观察,同样,日常生活也离不开观察.观察是人们对事物作出正确判断的前提.中医诊病的方法是:望、闻、问、切,望即观察,它是诊病的第一关键,通过观察病人的气色及病的程度和部位等形成第一感觉,为判断病情建立感性认识和客观依据.成语“胸有成竹”就是观察的结果.寓言故事“黔之驴”讲的就是老虎对驴子这个庞然大物,通过仔细观察,发现驴子好像没有什么特殊的本领,老虎基本掌握了驴子的特性,经过与驴子的博弈之后,咬断驴的喉咙,将它杀死,这充分说明了观察的重要性.如果老虎不去仔细观察驴子这个庞然大物,那么老虎可能就会远离驴子而去,而吃不到驴肉.
观察是科学认识的重要源泉,是获得感性认识的基本途径,观察可以诱导理论发现与技术发明,观察是检验科学理论的重要方法.
2 观察法在高等数学教学中的应用
高等数学是理、工、农、经、管等专业必修的一门重要的专业基础课程,其内容丰富、方法众多、思想性强,有许多概念和理论是比较抽象的,从而增加了学生学习高等数学的难度和枯燥程度.如何使得这些抽象的、枯燥的理论能让学生更容易理解和接受,使死的东西变成鲜活的知识,这是教师必须考虑的问题.教材只是记录了科学家发现的结果,很少涉及发现的过程,如果我们能观察教材、分析教材,创造性地按照知识发现过程来进行高等数学教学的话,无疑能激发学生的学习兴趣,使学生快乐地参与到高等数学的教学中来.结合教学实践,本文拟从以下几个方面介绍在高等数学教学中如何应用观察法,以及如何培养学生的观察能力.
2.1 顺序观察法
所谓顺序观察法,就是对观察客体选择不同的方向、不同的起点,按顺序条理分明地进行观察,从而作出准确判断.通常观察的顺序是从上到下、从前到后、从左到右、从外到内、从一阶到高阶、从一次到高次等等.
例1[4]设y=sinx,求y(n).
分析 因为没有直接求函数高阶导数的求导法则,更何况是求不确定的n阶导数,解决这类问题,只有按照顺序观察其一阶导数、二阶导数直至高阶导数,从中找出规律,进而写出n阶导数的通项公式.
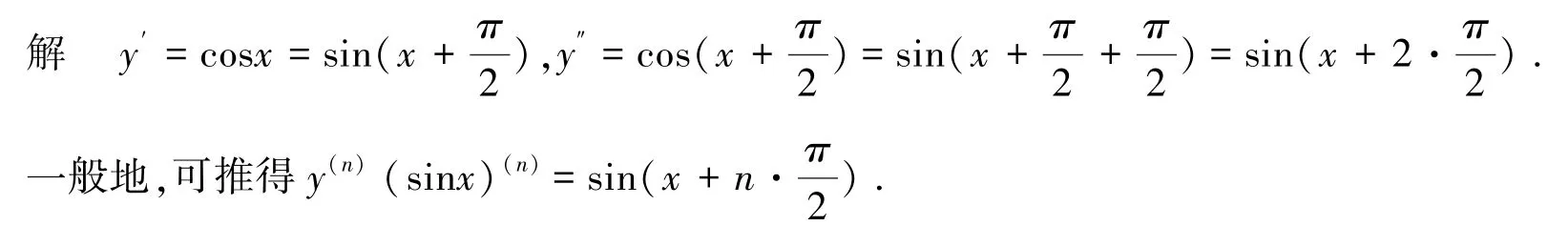
例2 将复合函数y=esin21x分解成基本初等函数.
分析 这类问题是从外到内进行观察分析.
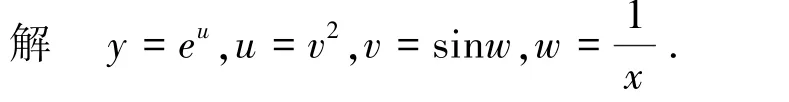
2.2 解剖观察法
一个整体通常是由部分组成的.我们将一个整体分割成部分来进行观察,通过观察各部分而得出整体的结果,这就是解剖观察法.如计算圆锥体的表面积,我们将其分割为底面和侧面两部分进行观察,通过解剖观察后得出,圆锥体的表面特征:底面圆和侧面展开成一个扇形,从而可以算出圆锥体的表面积.


2.3 对比观察法
对比观察法就是将两个或若干个相关联的事物对照比较,进行观察分析,从中发现它们的共性特征或本质区别,以获得清晰的概念或结论.
在介绍用导数判别函数的增减性时,我们首先将一个单调增加的函数y=f(x)和一个单调减少的函数y=g(x)进行对比观察,发现单调增加的函数其导数f′(x)≥0,相反,单调减少的函数其导数g′(x)≤0.由此,我们得出了函数单调性的必要条件以及判别函数单调性的充分条件这两个非常重要的结论.
再如,我们在研究函数的凹凸性时,将凹弧和凸弧放在一起加以对比观察,发现凹弧的切线位于其弧的下方,凸弧的切线位于其弧的上方这样两个鲜明的不同结论,由此我们引入了曲线凹凸的概念.
2.4 重点观察法
重点观察法就是在全面观察事物的基础上,对能反映事物本质特性的一个或几个关键部分作出特别仔细的观察,找出解决问题的途径.

2.5 全面观察法
全面观察法就是观察事物的全貌,观察事物的组成部分及各部分之间的相互关系及内在联系,进行整体分析得出结论.

通过以上证明,我们又不难发现,对m>0的任意实数极限都能成立.
3 结语
还有许多观察法我们没有涉及到,因为实践中没有必要说明是什么具体的观察法,只要能解决实际问题就行.当然,通过观察我们只能得出一个感性认识,这个认识是否正确,必须加以证明.有时可能提出错误的猜测.
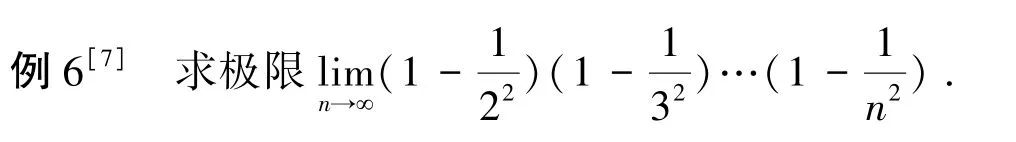
分析 如果我们按照例3中的方法来分析的话,因为数列是n个小于1的数的乘积,因此,我们猜测,当n→∞时,极限为0.事实上,这个猜测是错误的.
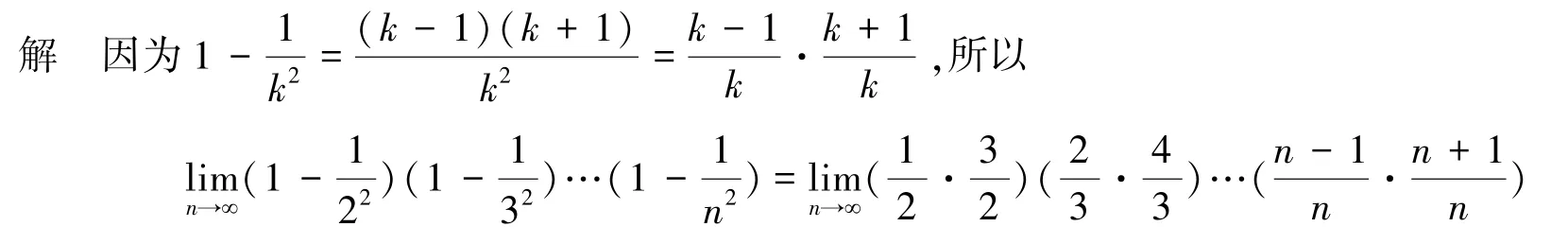
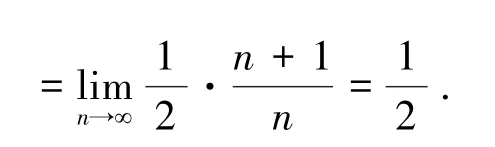
这是为什么呢?因为虽然两个数列都是n个小于1的数的乘积,但它们有本质的区别.

虽然这3个数列都是无数个小于1的因数的乘积,但它们的极限却大不相同.
在观察的同时,应伴有分析推理和归纳猜测.观察主体观察得越仔细、经验越丰富、分析推理得越合理,则归纳猜测的结论越正确.
观察是培养能力和发展智力的重要途径.在传授知识的同时,重视培养学生的观察能力,运用多种手段和题材,激发学生观察兴趣,通过教学使学生掌握正确的观察方法,获得良好的观察能力,逐步培养学生主动观察、善于观察的习惯,提高学生学习数学的能力,学会从数学角度去观察世界和认识世界.
[1]中国社会科学院语言研究所词典编辑室.现代汉语词典[K].北京:商务印书馆,2003.132,463.
[2]张雄,李得虎.数学方法论与解题研究[M].北京:高等教育出版社,2003.18-25.
[3]魏国新,郭兴进.观察、归纳和演绎在启发式数学教学中的作用[J].中国西部科技,2010,(20):69-70.
[4]辛小龙.高等数学[M].西安:西北大学出版社,2011.91.
[5]华东师范大学数学系.数学分析[M].北京:高等教育出版社,2011.34.
[6]陈文灯,吴振奎,黄惠青.高等数学解题方法和技巧[M].北京:中国财政经济出版社,2004.24.
[7]陈文灯,黄先开.考研数学复习指南[M].北京:世界图书出版公司,2010.36.
【责任编辑 牛怀岗】
Observation Method in Practice and Cognition of Teaching Advanced Mathematics
XUE Li-min
(School of Mathematics and Information Science,Weinan Normal University,Weinan 714099,China)
Observation is carefully checked.Observation is the starting point of scientific research and the source of all inventions.The several aspects of examples which are sequential observation method,anatomical observation method,comparative observation method,emphasis observation method and comprehensive observation method are introduced the application in teaching of observation method and clarified how to cultivate the observation ability of students in Advanced Mathematics.
observation;observation method;observation ability;Advanced Mathematics teaching
G642
A
1009-5128(2014)19-0009-05
2014-06-20
渭南师范学院教育教学改革研究重点项目:高等数学精品教材建设的研究与实践(JG201314)
薛利敏(1960—),男,陕西韩城人,渭南师范学院数学与信息科学学院教授,主要从事基础数学与运筹学研究.

