优化交错网格差分算子的井间地震数值模拟及其频散分析
章 阳,孟凡顺
(中国海洋大学 海底科学与探测技术教育部重点实验室,青岛 266100)
优化交错网格差分算子的井间地震数值模拟及其频散分析
章 阳,孟凡顺
(中国海洋大学 海底科学与探测技术教育部重点实验室,青岛 266100)
在井间地震有限差分数值模拟中,用离散化的高阶差分方程近似连续导数的波动方程时,不可避免地会产生数值频散,而数值频散程度则直接影响到地震波数值模拟精度,因此为了得到清晰准确的地震波场记录,必须尽可能地压制数值频散。这里在一阶速度应力弹性波方程的基础上,利用两个约束条件构造拉格朗日函数获取优化差分系数,与泰勒展开差分系数下的交错网格高阶差分模拟结果比较,发现改进的优化交错网格差分算子的高阶差分数值模拟能更有效地压制数值频散,进一步提高交错网格高阶差分数值模拟的精度,为高精度井间地震数据的波场成像、纵横波联合解释等提供可靠依据。
有限差分;数值频散;交错网格;约束条件;优化差分算子
0 引言
地震波数值模拟技术在复杂油气藏地震勘探开发中发挥着举足轻重的作用,可以通过地震波数值模拟方法研究地震波在复杂介质中的传播规律和响应特征,进而对实际地震资料的解释以及地震波的偏移反演等处理提供可靠依据[1]。井间地震与常规的地震勘探不同,它是将震源和检波器都放在井中,在一口井激发,相邻井接收。井间地震正演模拟是根据给定的数学模型、震源项、地下几何界面和物性参数研究波动方程的运动学和动力学特征。
有限差分法是目前井间地震数值模拟技术中应用最广泛的方法,其原理是将描述介质的微分方程,用差商近似微商,进而转化为有限差分方程进行近似求解。这种近似导致在有限差分数值模拟中不可避免地会产生数值频散问题[2]。用离散化的高阶差分方程去近似连续导数的波动方程,使相速度变成空间离散间隔和时间步长的函数,当每一波长内空间采样太少(如粗网格情况)时,便会产生数值频散,这是差分方程所固有的本质特征[3]。数值频散现象即计算精度问题,对于波动方程及其差分格式已经确定的情况下,频散现象随着空间采样间隔的减小而减小。Madariaga[4]首次提出交错网格有限差分法并用于一阶速度-应力弹性波方程中,数值模拟时不需要对弹性参数空间微分,减少计算量的同时有效地提高数值模拟的精度,数值频散得到有效地改善。Dablain[5]利用Taylor级数给出声波方程高阶差分格式,成功消除空间差分频散对数值模拟的影响,极大提高有限差分数值模拟的精度,同时还分析了时间和空间离散的频散特征。Virieux[6-7]利用交错网格有限差分法成功实现了各向同性介质中的SH波和P-SV波的模拟,计算精度为O(Δt2+Δx2),同时对交错网格与常规网格进行比较分析发现交错网格在不增加计算量的前提下精度提高了4倍。Alford和Dablain对有限差分数值模拟的影响因素(网格大小和地震波传播方向)进行分析,网格间距控制地震波数值模拟的精度。董良国[8]从理论上证明并分析了影响数值频散的主要因素,同时比较常规网格与交错网格有限差分算法产生的数值频散。吴国枕[9]从空间差分算子时间差分算子两方面详细分析了有限差分数值频散,并给出压制数值频散的方法即通量传输校正方法(FCT),取得较好的模拟效果。
本研究在前人研究成果的基础上,对于交错网格高阶有限差分的差分系数,采取最优化原理,通过构造拉格朗日函数求取条件极值获得优化的差分系数,比较原始差分系数和优化差分系数下的交错网格高阶有限差分模拟结果,表明优化的有限差分算法在计算效率相同的情况下能在一定程度上压制数值频散,提高模拟精度。
1 一阶速度-应力弹性波方程有限差分数值模拟
在本研究中,主要以一阶速度-应力弹性波方程为基础。二维TI介质中,一阶速度-应力弹性波方程(假设体力为零)[10]为:

其中:vi为速度分量;σxx、σzz分别为x和z方向的正应力;σxz为剪应力;ρ为介质密度;Cij为介质弹性参数。在各向同性的TI介质中,
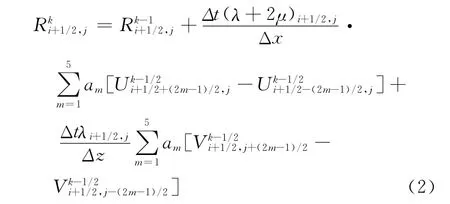
在弹性波高阶有限差分数值模拟中,实际介质是无限大的,而计算时却是在一个有限的区域,导致在数值模拟时会引入人工边界反射问题。本研究采取完全匹配层吸收边界条件(PML)实现对弹性波方程数值模拟的边界处理[13]。PML的核心思想是在计算区域外面构造有限厚度的吸收层,吸收层吸收或衰减向外传播的波,同时在计算模型区域与吸收层的链接处是透明的,使得产生最小可能的虚假反射来解决模拟时的人工边界问题。以σxx为例,根据完全匹配层的分裂思想,则时间2阶,空间10阶精度的交错网格高阶差分格式为:
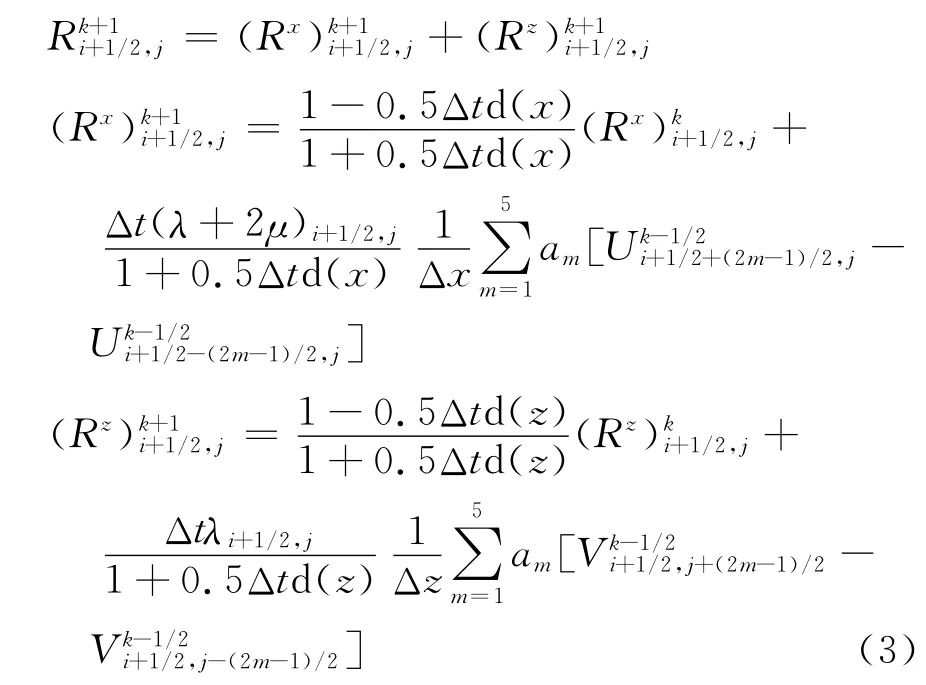
在高阶有限差分算法中,用离散化的高阶差分方程近似连续导数的波动方程,必定不可避免会产生一定的误差。随着传播时间的推移,下一时间的离散点处必定积累上一时间的网格离散导致的计算误差,从而造成数值模拟结果的不稳定性。误差大小又与所选择的模型参数有关,参数选择不合理,必然导致数值结果精度低,网格频散严重等。因此对有限差分稳定性的分析是衡量数值模拟时参数设置是否合理的问题,本研究采用董良国[14]提出的一阶速度-应力弹性波方程交错网格高阶差分稳定性分析条件进行数值模拟。
2 优化有限差分算子
在地震波数值模拟中,目前使用最普遍的是交错网格高阶有限差分法,可以有效地降低数值频散,提高模拟精度。交错网格高阶差分算子是通过泰勒展开求取的,本研究换另外一种思路,应用拉格朗日乘数法,构造拉格朗日函数,运用条件极值求得新的交错网格差分算子。
有限差分法数值模拟是用离散的差分算子近似替代连续的微分算子,因而会产生误差,造成数值频散。当离散差分算子无限接近连续微分算子时,产生的误差就会很小,提高模拟精度,降低数值频散。基于这一原理,令表示在xi处的一阶偏导数差分算子表示在xi处的一阶偏导数微分算子,当接近“1”时,差分算子代替微分算子误差小,近似精度高。
定义函数
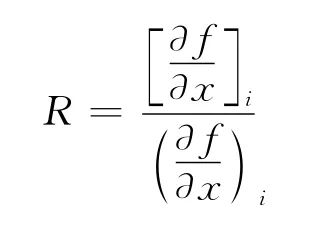
根据前人的研究,应用拉格朗日乘数法,引入两个约束条件:
条件极值为:
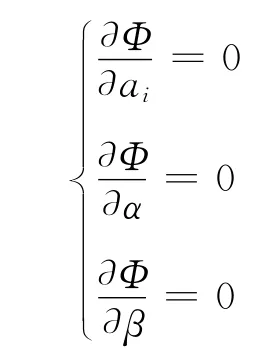
根据数值实验选取l0=0.4、β=-12便可求得一组优化差分系数:a1=1.250561、a2=-0.119 811、a3=0.031 364、a4=-0.009 179、a5=0.001 812。
3 数值模拟算例
3.1 各向同性单层均匀介质模型
设计一个各向同性的单层均匀介质模型,模型大小为3 000 m×3 000 m,空间网格采样步长Δx=Δz=10 m,时间采样步长Δt=1 ms,纵波速度vp=2 000 m/s,泊松比为0.25,密度ρ=2 000 kg/m3,震源子波选用主频为30 Hz的雷克子波,位于模型中央,激发井和接收井位置分别位于水平1 500 m和2 000 m处,等能量激发震源。模型参数满足交错网格高阶差分数值模拟的稳定性条件,采用完全匹配层的吸收边界(PML),完全匹配层的层数为δ=50,理论反射系数R=1e-6。数值模拟的精度为O(Δt2,Δx10),比较两种不同差分系数的波场快照,其中(0,1 500 m)是泰勒展开差分系数的波场快照,(1 500 m,3 000 m)是优化差分系数的波长快照。图1是t=850 ms的混合波场的增益波场快照。

图1 t=850 ms时刻混合波场的增益波场快照Fig.1 The gain wave field snapshot of mixed wave field,t=850 ms
分析图1,当波长快照增益倍数增大时,常规的交错网格高阶有限差分数值模拟仍会产生较为严重的数值频散,影响计算精度。比较混合波场快照的上下两部分,显然优化差分系数的交错网格高阶差分法相比泰勒展开的常规差分系数的交错网格高阶差分法,在一定程度上能更好地压制数值频散。对于横波的频散压制效果较为明显,对于纵波也能压制,但效果不明显,通过提高增益倍数能观察到频散的压制。由于改进的优化差分系数交错网格高阶差分法主要是针对差分系数,通过不同的数学方法求取新的差分系数,运算效率没有改变。因而采用优化差分系数交错网格高阶差分法进行数值模拟能达到常规交错网格高阶差分法的运算效率,同时能够在一定程度上压制数值频散,提高计算精度,使波场清晰,有利于分析地震波的波场特征。
3.2 corner-edge模型
设计一个二维corner-edge模型(图2),模型大小为5 000 m×5 000 m,空间网格采样步长Δx=Δz=10 m,时间采样步长Δt=1 ms,第一层纵波速度为vP=1 500 m/s,泊松比为0.25,第二层纵波速度vP=3 500 m/s,泊松比为0.4,密度ρ=2 000 kg/m3,震源子波选用主频为30 Hz的雷克子波,位于模型中央,激发井和接收井位置分别位于水平2 500 m和4 000 m处,纵波震源激发。模型参数均满足交错网格高阶差分数值模拟的稳定性条件,完全匹配层的层数为δ=50,理论反射系数R=1e-6。数值模拟精度为O(Δt2,Δx10),比较两种不同差分系数的增益波长快照。图3(a)为常规泰勒展开
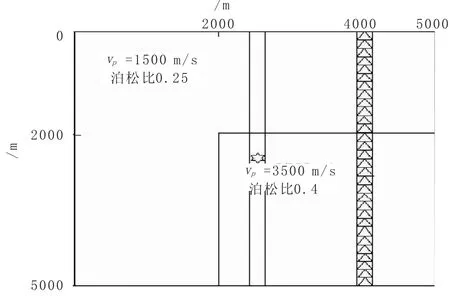
图2 二维corner-edge模型Fig.2 Two-dimensional corner-edge model
差分系数的交错网格高阶差分法记录的混合波场的增益波场快照,图3(b)为优化差分系数的交错网格高阶差分法记录的混合波场的增益波场快照。观察图3(a)发现,常规差分系数的交错网格高阶差分数值模拟的增益波场快照出现较为严重的数值频散,影响模拟的精度。当用优化差分系数的交错网格高阶差分数值模拟时,观察图3(b)能一定程度地压制频散,但仍然不能完全消除频散。图中标出的位置即为压制数值频散较为明显的位置,效果比较好。
3.3 Marmousi模型
图4为Marmousi模型,模型网格大小为3 401 ×701,空间网格采样步长Δx=Δz=10 m,时间采样步长Δt=0.5 ms,模型上层是深度为900 m的海水层,下层为模型的纵波速度场。震源子波选用主频为30 Hz的雷克子波,炮点位于(17 000 m,10 m),检波点放在920 m深的位置,道间距10 m,纵波震源激发,记录长度为6.5 s。完全匹配层的层数为50,理论反射系数R=1e-6。数值模拟的精度为O(Δt2,Δx10),图5为两种不同差分系数混合波场的单道增益反射波地震记录图。
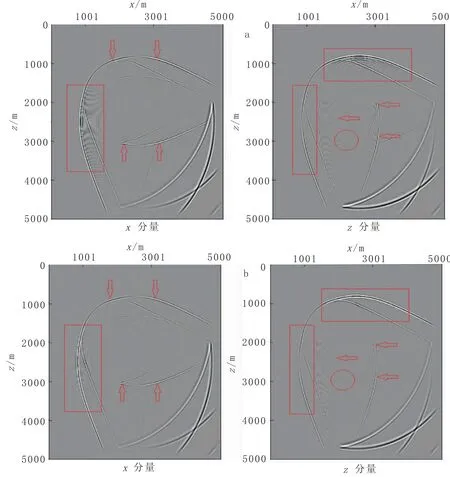
图3 t=1 s时刻混合波场的增益波场快照Fig.3 The gain wave field snapshot of mixed wave field,t=1 s
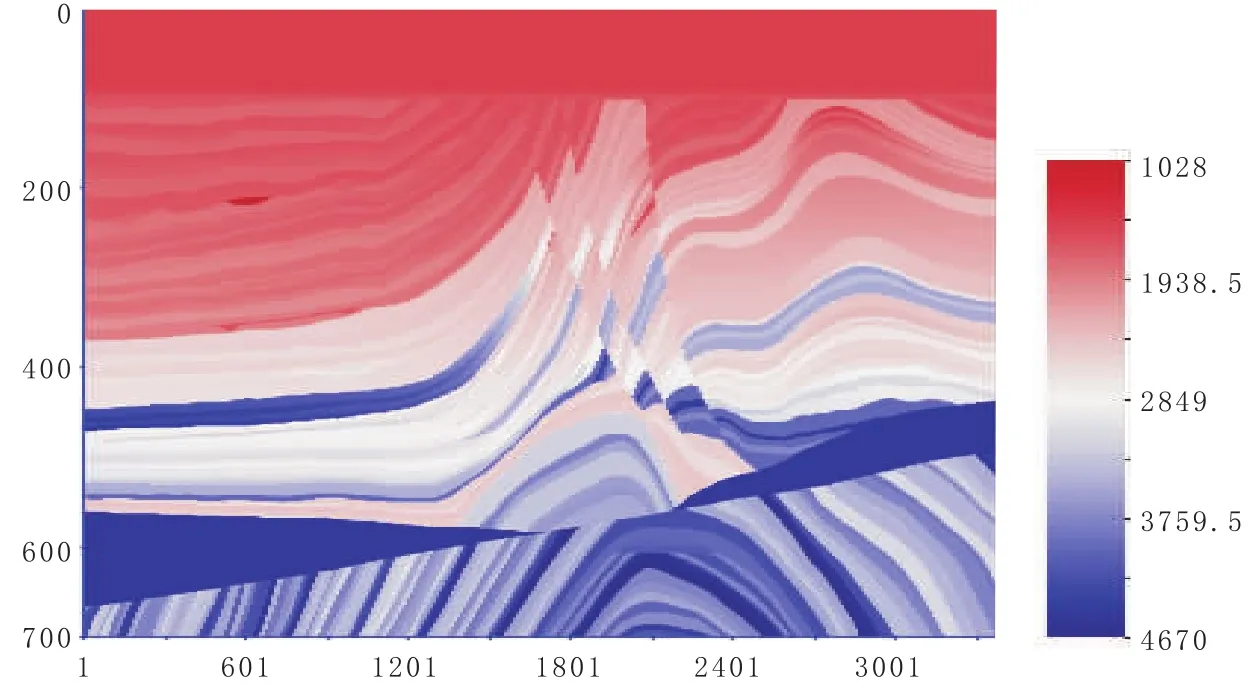
图4 Marmousi模型(横纵坐标均为网格点数)Fig.4 Marmousi model
交错网格高阶差分法研究复杂Marmousi模型,对比常规差分系数交错网格高阶差分法和优化差分系数交错网格高阶差分法的单道增益反射波地震记录,数值频散有一定地改善。
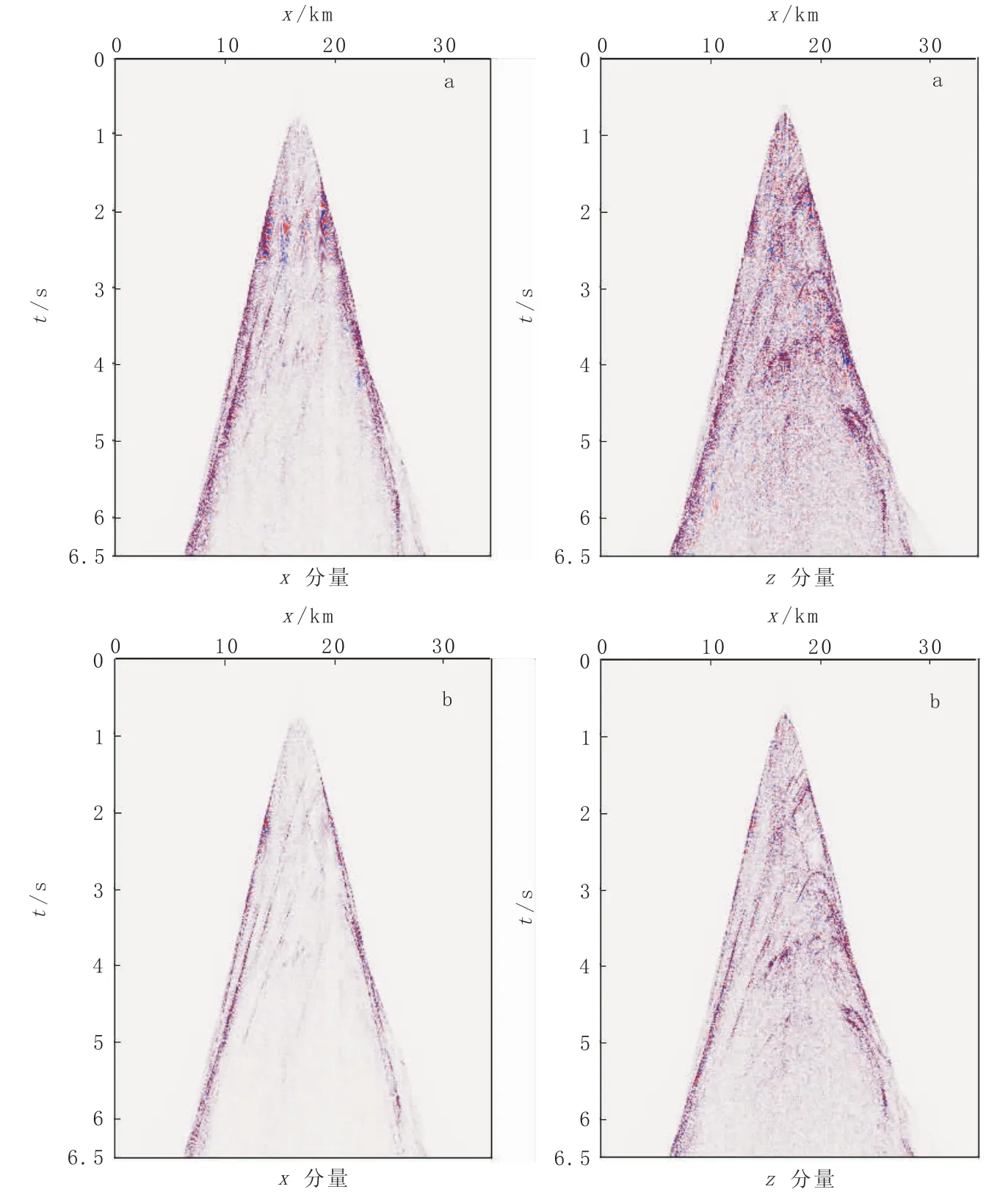
图5 Marmousi模型混合波场单道增益地震记录图(去直达波后反射波地震记录)Fig.5 The single channel gain seismograms of mixed wave field with Marmousi model
4 结论
井间地震数值模拟中,用离散化的高阶差分方程近似连续导数的波动方程,不可避免地产生了数值频散问题。数值频散会导致波形畸变或重影,严重影响波场特征。交错网格高阶差分法可以提高计算精度,压制数值频散。本研究在交错网格高阶差分法的基础上进行改进,利用构造拉格朗日函数的方法,根据约束条件求取条件极值得到新的交错网格差分系数。比较优化差分系数的交错网格高阶差分法和常规差分系数的交错网格高阶差分法的数值模拟结果。通过结果表明,优化差分系数法能更有效地压制数值频散,提高计算精度。因此在今后的地震波数值模拟时,可以采用本文改进的优化差分系数法提高计算精度,更好地压制频散,分析地震波场的特征。
[1] 牟永光,裴正林.三维复杂介质地震数值模拟[M].北京:石油工业出版社,2005.
[2] 蔡其新,何佩军.有限差分数值模拟的最小频散算法及其应用[J].石油地球物理勘探,2003,38(3):247-251.
[3] 李国平,姚逢昌,石玉梅,等.有限差分法地震波数值模拟的几个关键问题[J].地球物理学进展,2011,26(2):469-476.
[4] MADARIAGA R.Dynamic of an expanding circular fault[J].BSSA,1976,66(3):639-666.
[5] DABLAIN M A.The application of high-order differencing to scalar wave equation[J].Geophysics,1986,51(1):54-66.
[6] VIRIEUX J.SH-wave propagation in heterogeneous media:Velocity-stress finite difference method[J].Geophysics,1984,49(11):1933-1941.
[7] VIRIEUX J.P-SV wave propagation in heterogeneous media:Velocity-stress finite difference method[J].Geophysics,1986,5(4):1889-1893.
[8] 董良国,李培明.地震波传播数值模拟中的频散问题[J].天然气工业,2004,24(6):53-56.
[9] 吴国枕,王华忠.波场模拟中的数值频散分析与校正策略[J].地球物理学进展,2005,20(1):58-65.
[10]董良国,马在田,等.一维弹性波方程交错网格高阶差分解法[J],地球物理学报,2000,43(3),411-419.
[11]陆基孟,王永刚.地震勘探原理[M].北京:中国石油大学出版社,2011.
[12]刘喜武.弹性波场论基础[M].青岛:中国海洋大学出版社,2008.
[13]COLLINO F,TSOGKA C.Applications of the perfectly matched absorbing layer model to the linear elastic dynamic problem in anisotropic heterogeneous media[J].Geophysics,1999,66(1):294-307.
[14]董良国,马在田,曹景忠.一阶弹性波方程交错网格高阶差分解法稳定性研究[J],地球物理学报,2000,43(6):856-864.
Optimized staggered grid finite-difference numerical simulation of well seismic and analysis of numerical dispersion
ZHANG Yang,MENG Fan-shun
(Key Laboratory of Submarine Geosciences and Prospecting Techniques,Ministry of Education,Ocean University of China,Qingdao 266100,China)
In the finite-difference numerical simulation of well seismic,when using discretized higher-order differential equation approximate continuous derivative wave equation,it will inevitably lead to numerical dispersion.As numerical dispersion directly affects the precision of numerical simulation of seismic wave,so in order to get more clear and accurate records of seismic wave field,we must try best to suppress numerical dispersion.In this paper,we are based on an order velocity-stress elastic wave equation,introducing two constraint conditions and construct a Lagrange function,then obtain new differential coefficients by extremely conditions.Analyze and compare the numerical simulation of an order velocity-stress elastic wave equation with high-order staggered grid differential operators by Taylor expansion and optimized differential operators,we conclude that the numerical simulation using by optimized staggered grid differential operators can more effectively suppress the numerical dispersion and improve the accuracy of simulation.and provide a reliable basis for wave field imaging of high precision seismic data in well and interpretation between P wave and S wave.
finite-difference;numerical dispersion;staggered grid;constraint condition;optimized differential operator
O 175.8
A
10.3969/j.issn.1001-1749.2014.05.17
1001-1749(2014)05-0606-07
2014-02-18 改回日期:2014-06-06
国家基金课题(41174157)
章阳(1989-),男,硕士,主要从事地震波传播理论的正反演方法研究、有限差分数值模拟和射线追踪正演模拟,E-mail:zyzhang-08@163.com。

