导体棒在磁场中的转动问题研究

黄涛

（宜城市第一高级中学 湖北襄阳 441400）

曹立锋

（宜城市第三高级中学 湖北襄阳 441400）

导体棒在磁场中的转动问题研究

黄涛

（宜城市第一高级中学 湖北襄阳 441400）

曹立锋

（宜城市第三高级中学 湖北襄阳 441400）

用经典物理的方法研究了导体棒在磁场中的转动规律，并用MathCAD2001软件进行了数值模拟．

导体 磁场 转动 求解数值 模拟

1 题目

如图1所示，一半径为R的半圆形光滑轨道竖直放置（导轨电阻忽略不计），以过最低点的向右切线为x轴，以竖直向上为y轴建立平面直角坐标系x Oy．在y＞0范围内存在一垂直纸面向里的磁场，磁感应强度B与坐标值y成正比，即B＝ky（k＞0）．在半圆形轨道上有一根导体棒质量为m，电阻为r，导体棒所对的圆心角为α，导体棒左端与轨道的左端最高点对齐．当把导体棒由静止释放时，试分析导体棒的运动规律．

图1

2 规律分析

2．1 导体棒的动力学方程

设某一时刻导体棒的A点转过θ角，此时导体棒的角速度为ω＝，固定转轴的刚体的动力学方程［1］

式（1）中I为导体棒的转动惯量，α为导体棒所对的圆心角，L为导体棒中心到O′的距离为导体棒角加速度，M安为导体棒的安培力矩．

2．2 导体棒的转动惯量［1］

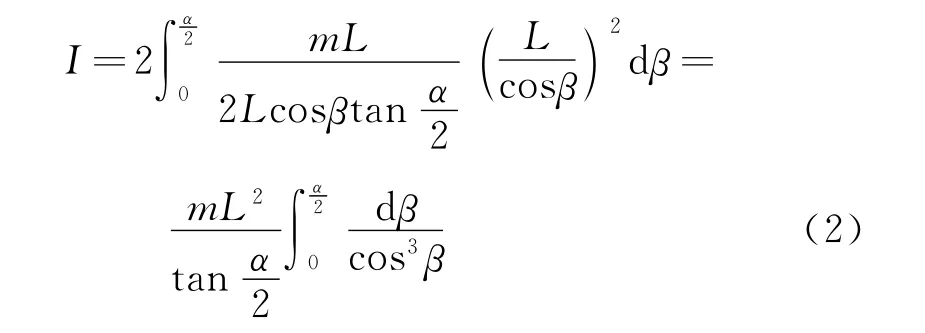
2．3 导体棒的感应电动势［2］

以棒的中点为界，下半部分与上半部分的切割速度方向相反，导体棒在图示位置时，设质心的角速度为ω＝θ·，导体棒各点的速度在沿棒方向上的分量均为Lθ·，导体棒上的D点对应的磁感应强度为

根据对称性可知导体棒的上半部分对应的电动势为

2．4 安培力的合力矩

安培力的合力矩的方向为顺时针方向与重力的力矩方向相反，所以导体棒的动力学方程为

由于导体棒的转动惯量为

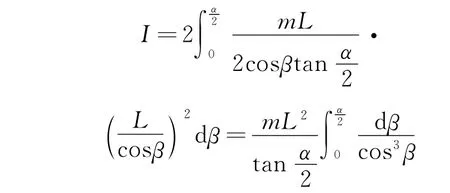
可得导体棒运动的微分方程

式中的两个定积分可以查表［3］求出．

2．5 用MathCAD2001数值模拟

图2 转过的角度与时间关系图

图3 感应电流与转过的角度的关系

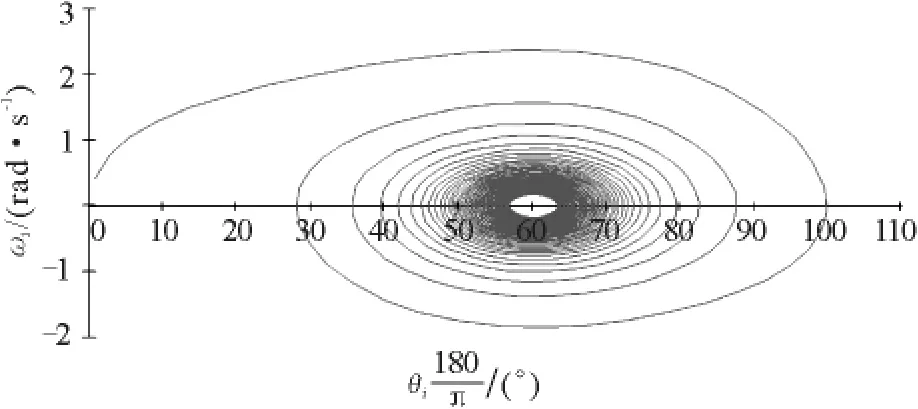
图4 导体棒的角速度与转过的角度的关系

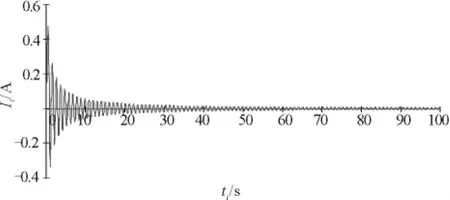
图5 感应电流与时间的关系图

3 图像分析

由图2和图5可知导体棒的运动为阻尼振动，因为导体棒减少的机械能转化为电能，所以它转动的最大角度在减小，最后会停止在圆轨道的最低点，此时角度为60°；由图3可知导体棒在运动到最低点的过程中，感应电流先增大后减小，再向右运动过程中感应电流反向先增大后减小，以后周而复始但最大电流在减小；由图4可知导体棒在下降的过程中角速度先增大后减小，以后周而复始但最大角速度在减小．

1 周衍伯．理论力学教程（第二版）．北京：高等教育出版社，1997．186～188，173～175

2 赵凯华，陈熙谋．电磁学（下册）（第二版）．北京：高等教育出版社，1997．479～485

3 四川大学数学系高等数学教研室．高等数学（物理类专业用第三版第一册）．北京：高等教育出版社，1997．372～373

2014- 05- 05）